


\text{Github Repository}

\text{Publication}
\text{Unsupervised Image } \newline
\text{Denoising with Parametric} \newline \text{ Noise Models}
\text{\textbf{Manan Lalit}, Mangal Prakash, Pavel Tomancak}
\newline
\text{Alex Krull, Florian Jug}
\text{Recap}






\text{Noisy Image}
\newline
\text{Stack (\textit{Input})}
\text{Clean GT }
\newline
\text{Stack (\textit{Target})}
Weigert et al, Content Aware Image restoration: Pushing the limits of Fluoroscence Microscopy, Nature Methods 15, pages 1090–1097 (2018)
\text{Noise2Void}




\text{Publication}
\text{Alex Krull}
\text{Tim-Oliver Buchholz}
\text{Florian Jug}
Krull and Buchholz et al, Noise2Void - Learning Denoising From Single Noisy Images, CVPR 2019


Krull et al, Probabilistic Noise2Void: Unsupervised Content-Aware Denoising, Frontiers in Computer Science, 2020


\text{Tomáš Vičar}
\text{Supervised Image Denoising (e.g. CARE)}





\text{Publication}
\text{Alex Krull}
\text{Florian Jug}
\text{Pavel Tomancak}
\text{Mangal Prakash}
| 18958 |
|---|
| 20758 |
| 20701 |
| 22378 |
| 18473 |
| 20397 |
| 19523 |
| 18295 |
| ... |
| 21845 |
| 20295.52 |
|---|

100
8
7
6
5
4
3
2
1
1
# pixels
# pixels
1
\text{Extracting Noise Model from Calibration Samples}
100
1
2
3
99
98





| 2930 |
|---|
| 2721 |
| 3369 |
| 3061 |
| 2369 |
| 3245 |
| 2987 |
| 2809 |
| ... |
| 3210 |
| 3004.32 |
|---|
\text{Noisy observations} \left( x \right)
1
2
3
4
5
6
7
8
100
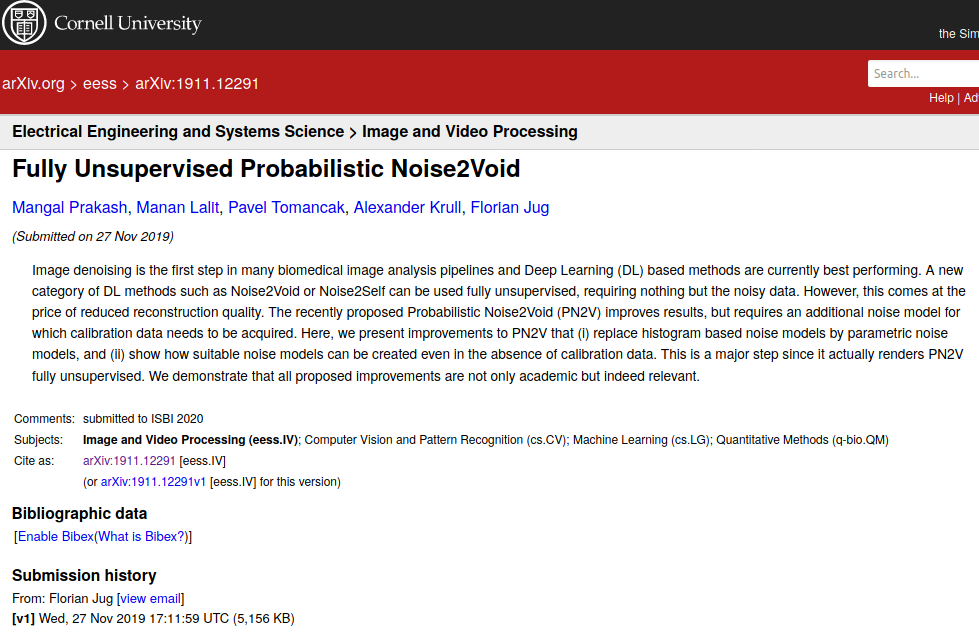
P(x|s=3004.32)=?
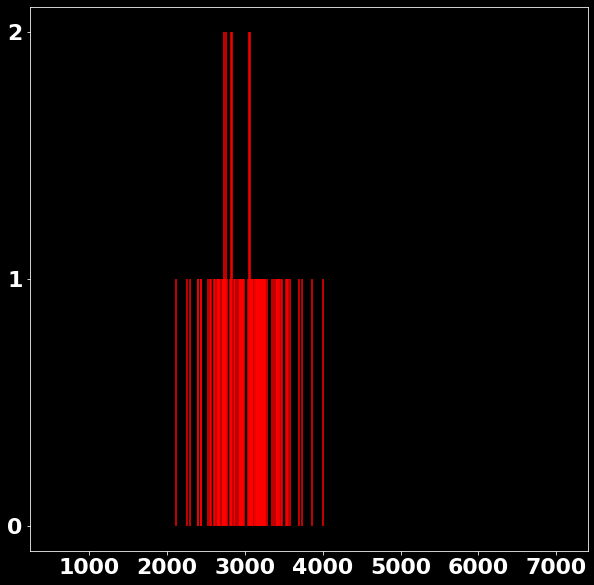
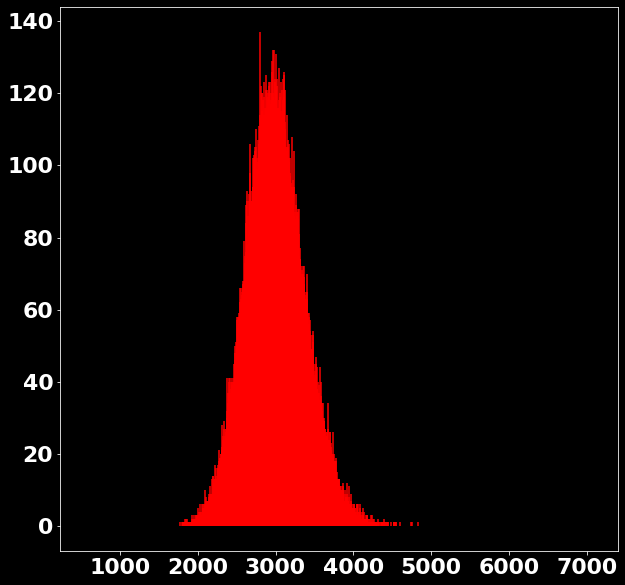
P \left(x|s \in [2978, 3006) \right)=?
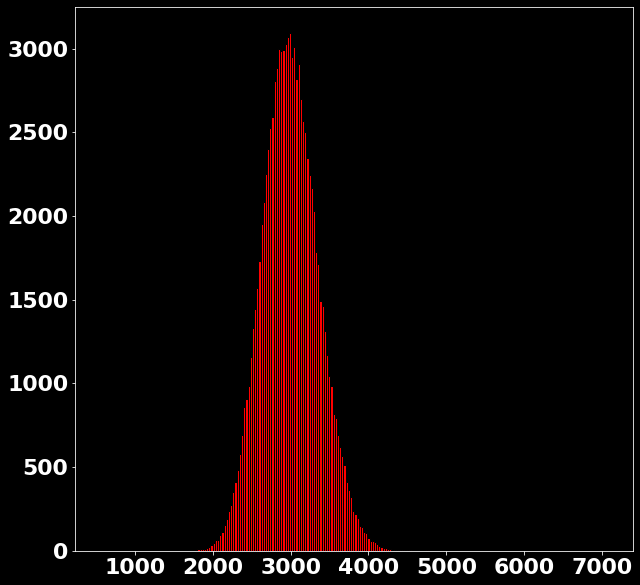
P \left(x_{\text{bin}}|s \in [2978, 3006) \right)=?
\text{Counts}
\text{Investigating the Noisy Calibration Pixels}
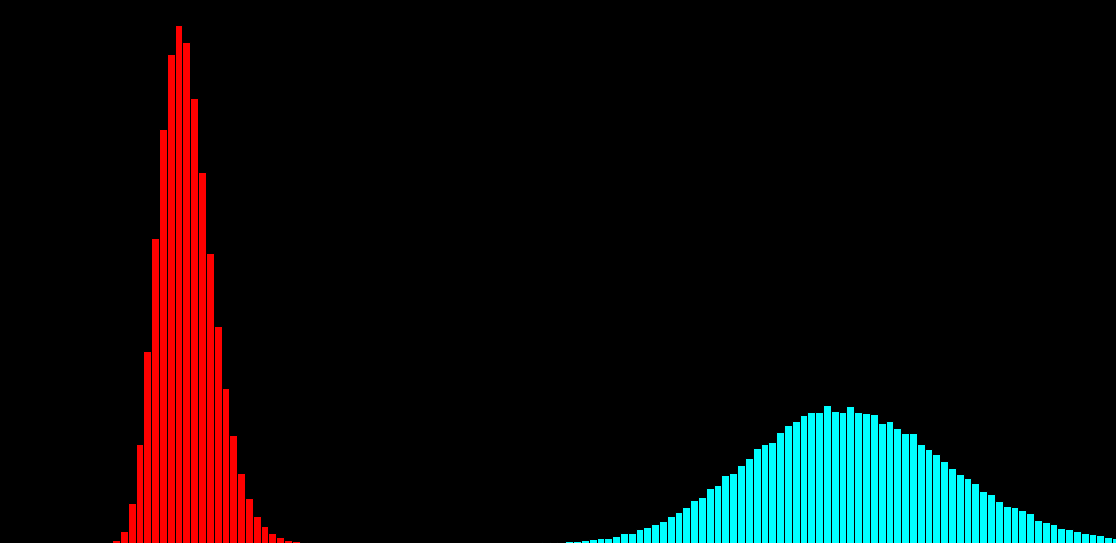



P(x|s)
\text{Noisy observation} \left( x \right) \text{bins}
\text{Noisy observation} \left( x \right) \text{bins}
\text{Clean signal} \left( s \right) \text{bins}
\text{Binning the Noise Model}
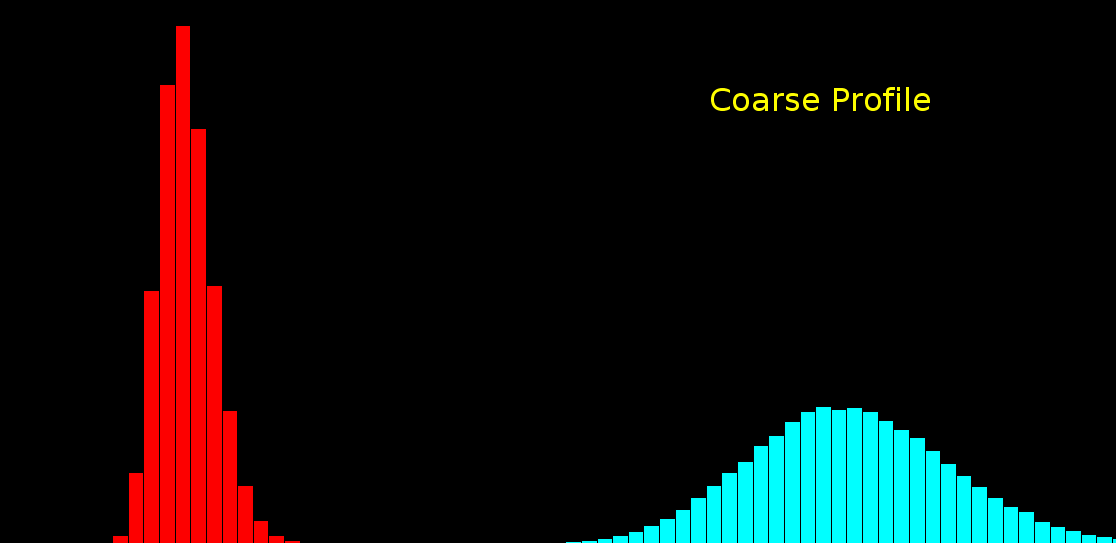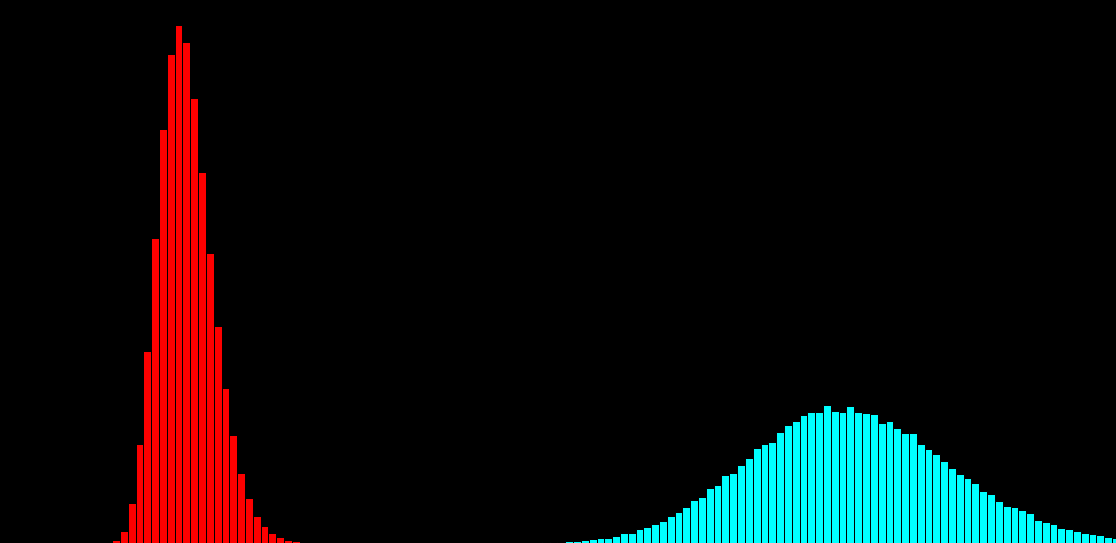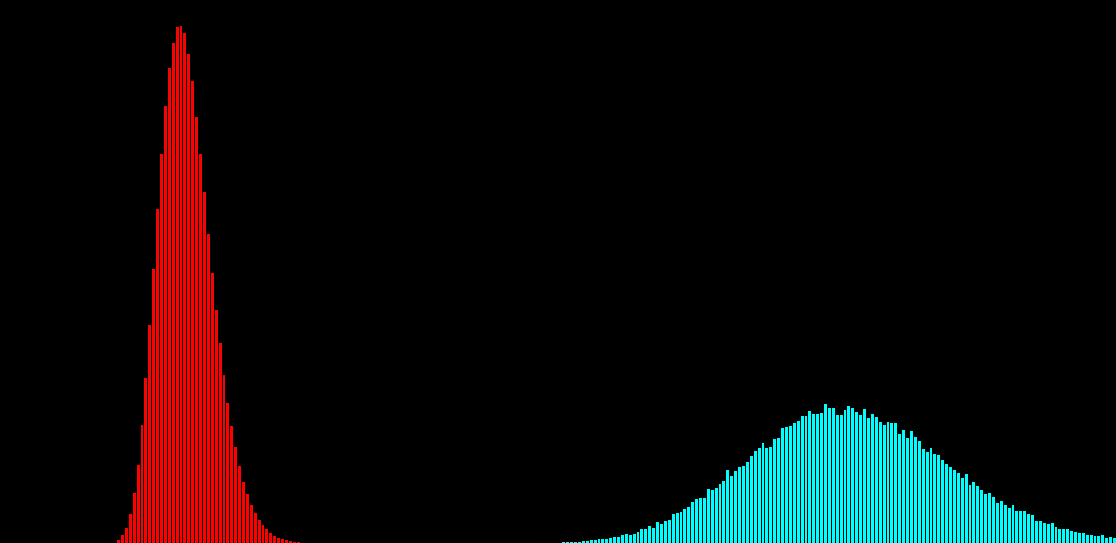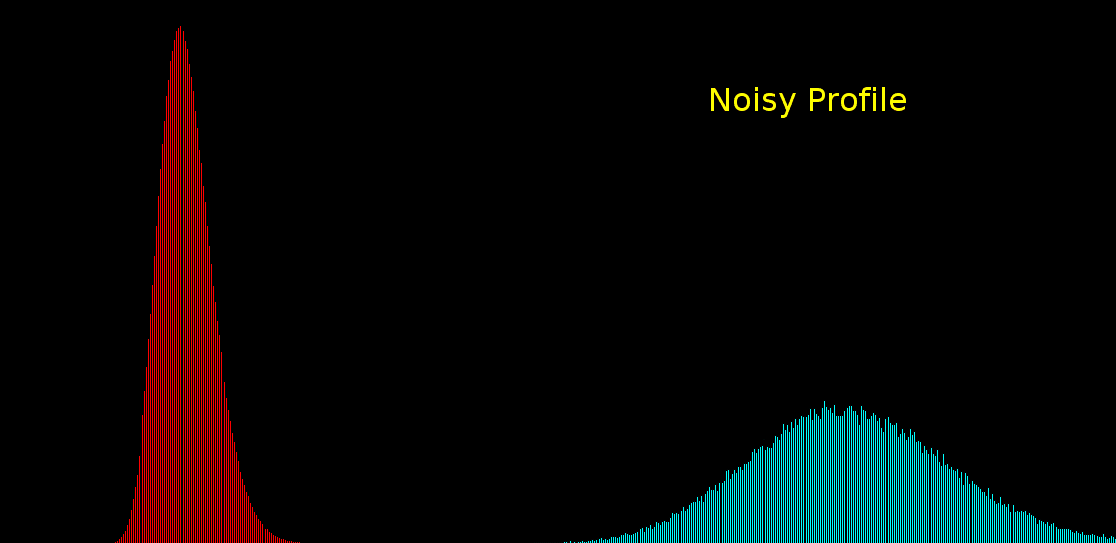
\text{Histogram-based Noise Model has some drawbacks ...}


100
99
98
3
2
1

\text{Noisy observation} \left( x \right) \text{bins}
\text{Clean signal} \left( s \right) \text{bins}
\text{Histogram-based Noise Model has some drawbacks ...}


p(x_i|s_i) = \sum_{k=1}^{K} \alpha_{k} f\big( x_i; \mu_{k},\sigma^{2}_{k} \big)
p(x_i|s_i) = \sum_{k=1}^{K} \alpha_{k}(s_{i}) f\big( x_i; \mu_{k} (s_{i}),\sigma^{2}_{k} (s_{i}) \big)
\hat{\theta} = \hat{a}, \hat{b}, \ldots = \text{arg max}_{\theta} \sum_{i,j} \log p \big( x_{i}^{j}| s_{i})
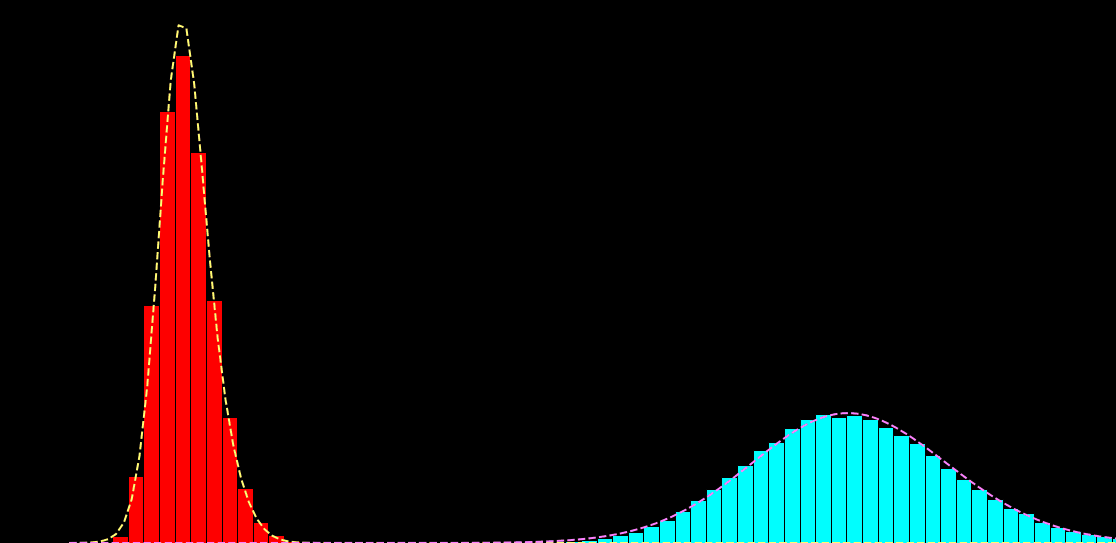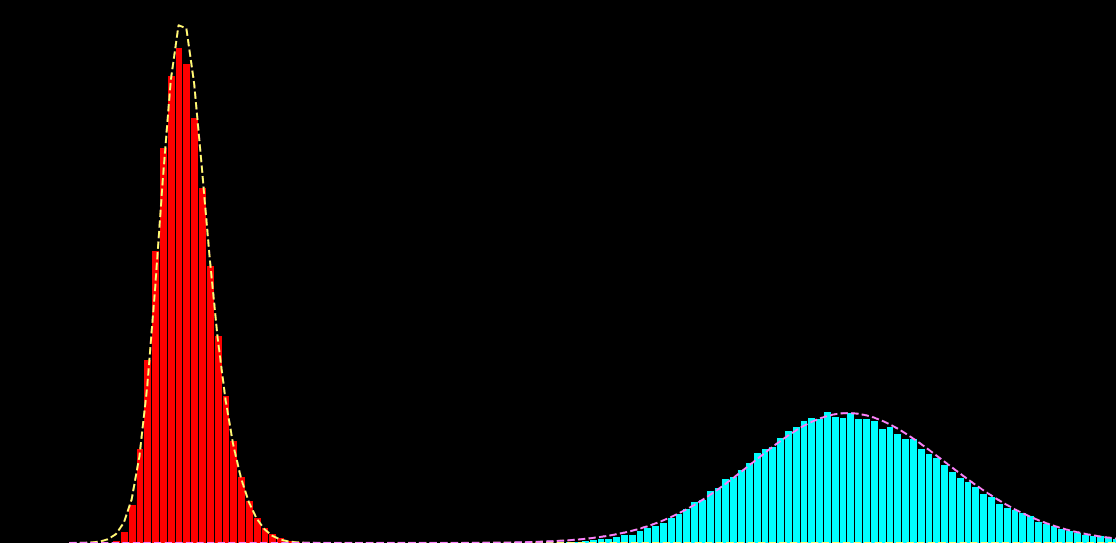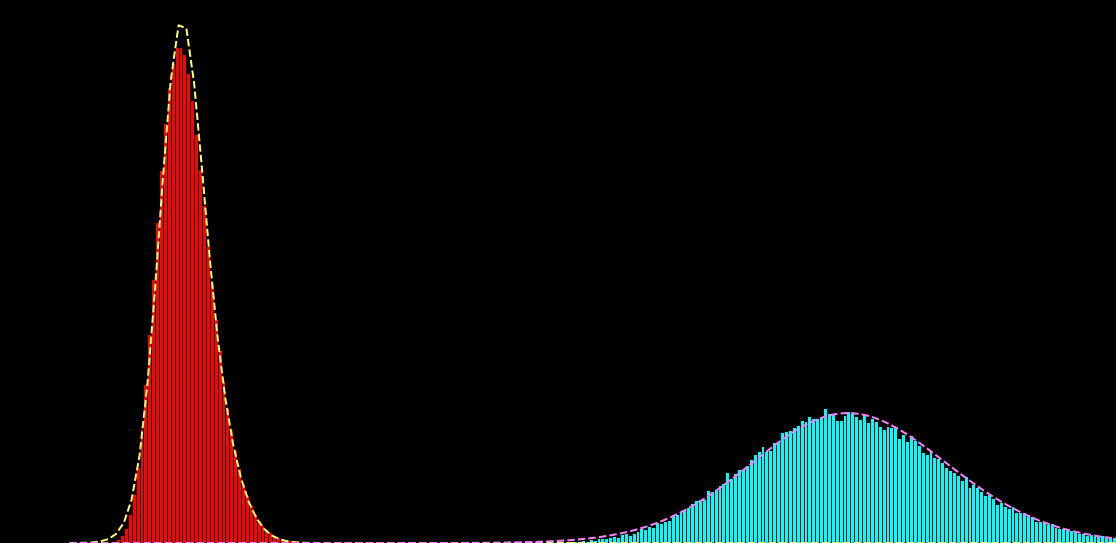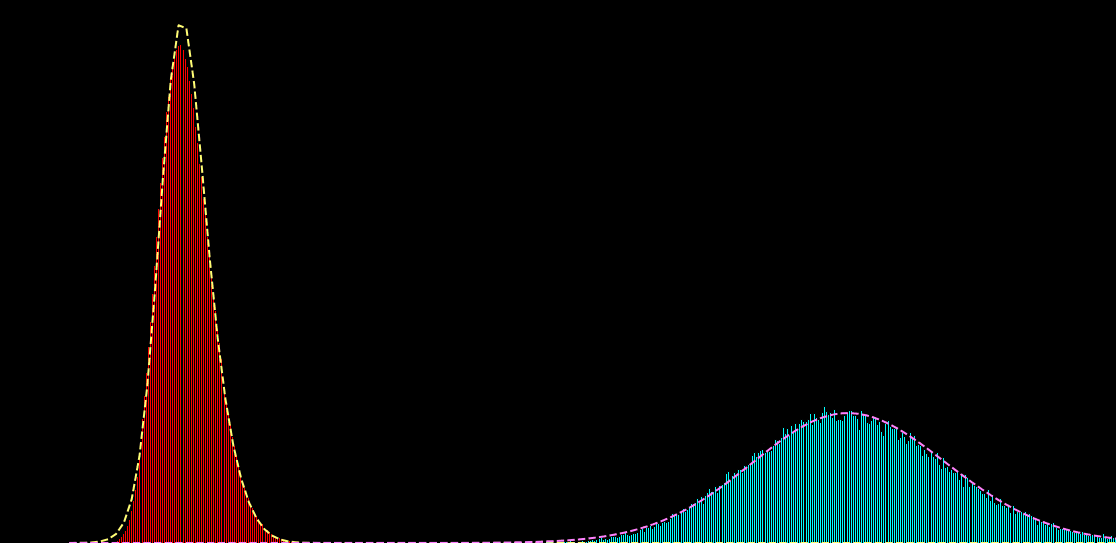
x_{i} : \text{noisy observation}
s_{i} : \text{ground truth signal}
K: \text{number of gaussians}
\alpha_{k} : \text{weight of gaussian $k$}
\mu_{k} : \text{mean of gaussian $k$}
\sigma_{k}^{2} : \text{variance of gaussian $k$}\\
\mu_{k} \left( s_{i} \right) = a + b \times s_{i} + c \times s_{i}^{2} + \ldots\\
\sigma_{k} \left( s_{i} \right) = \ldots
\alpha_{k} \left( s_{i} \right) = \ldots
\theta
\}
\text{Could we use a Parametric Noise Model?}






















\text{Calibration Data}




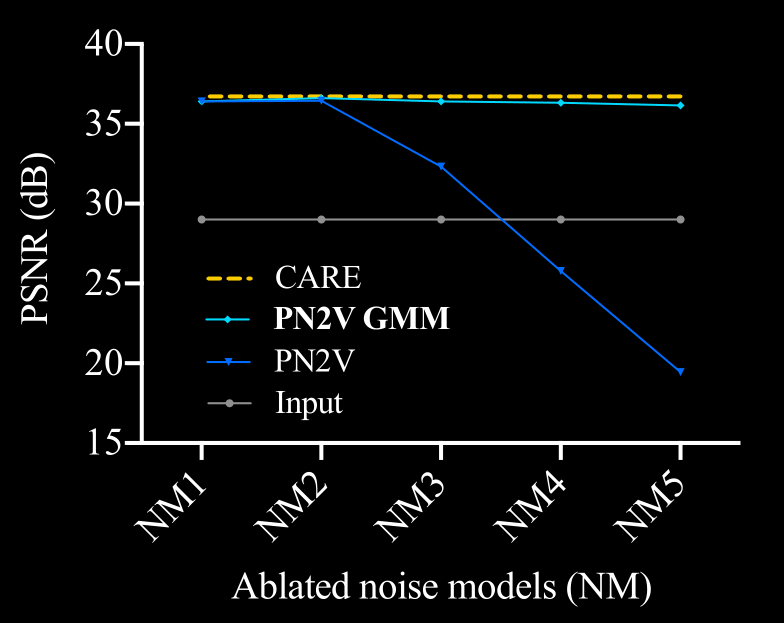
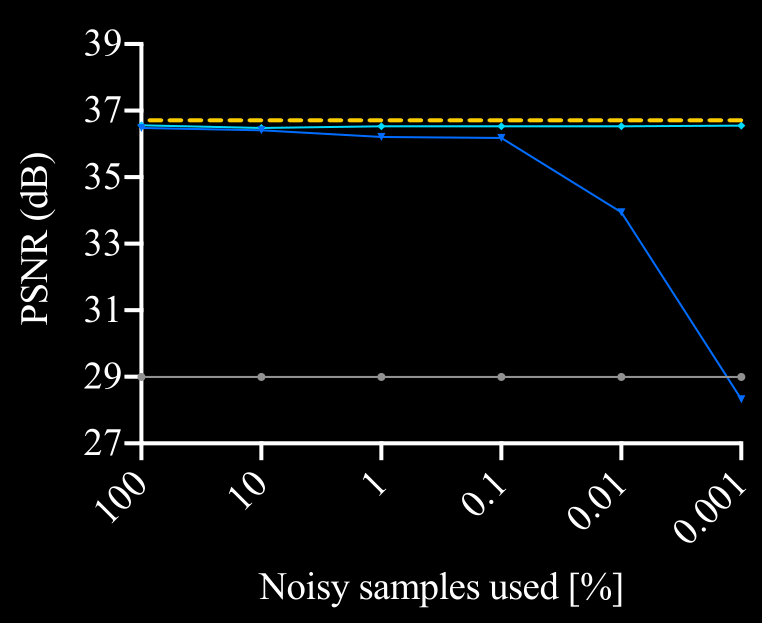
\text{Ablation Study Results}

\text{Image to be denoised}
\text{Input zoom}
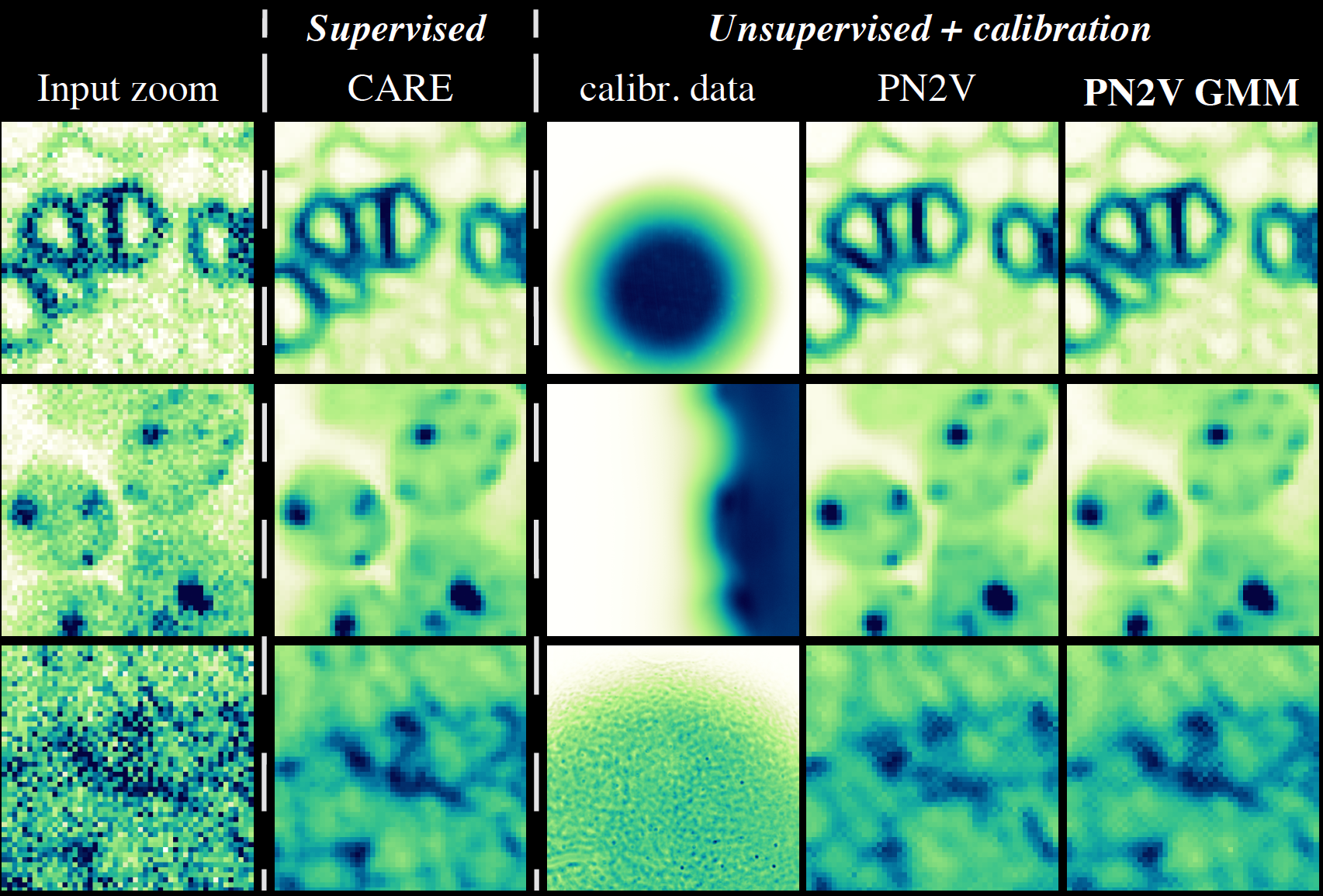
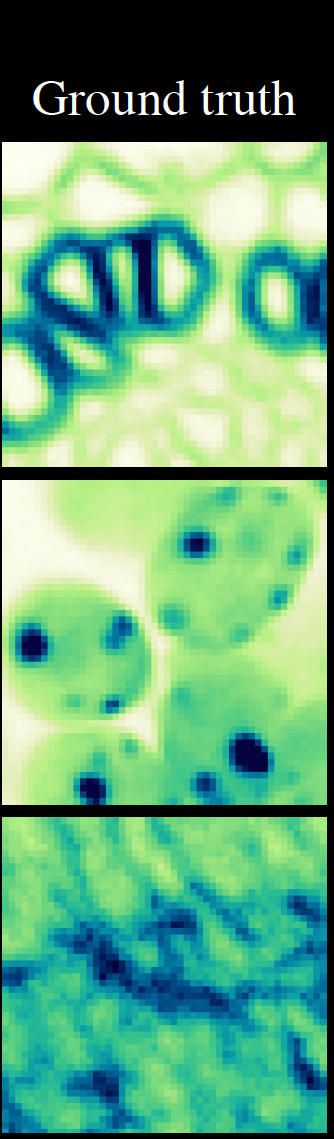

\text{PN2V GMM
}

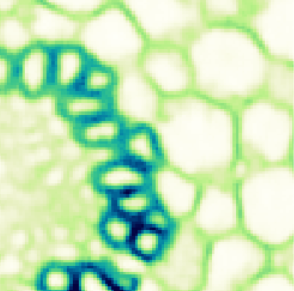

\text{Noisy Observation}
\text{Pseudo Ground Truth}
\text{PN2V Prediction}
\text{PN2V}
\text{N2V}
\text{Hist/GMM} \newline
\text{based } \newline
\text{Noise Model}
\text{But what if calibration data is not available ...
}





\text{Boot. GMM \& Boot. Hist.}

\text{Github Repository}
\text{Future Directions
}
\text{Application of \textbf{PN2V GMM} \& \textbf{Boot. GMM}}
\newline
\text{ to a diversity of biological data}
\text{\textbf{Joint} estimation of noise model and \textbf{PN2V} training}
\newline
\text{instead of the current \textit{sequential} route}



















\text{Acknowledgements}
\text{Thank you for listening!}
\newline
\text{Any questions?}
\text{Alex Krull}
\text{Matthias Arzt}
\text{Tim-Oliver Buchholz}
\text{Mangal Prakash}
\text{Anna Goncharova}
\text{Nuno Martins}
\text{Tobias Pietzsch}
\text{Deborah Schmidt}
\text{Florian Jug}
\text{Pavel Tomancak}
\text{Gabriella Turek}
\text{Marina Cuenca}
\text{Giulia Serafini}
\text{Vladimir Ulman}
\text{Bruno Vellutini}
\text{Johannes Girstmair}
\text{Mette Thorsager}