RL Food gathering
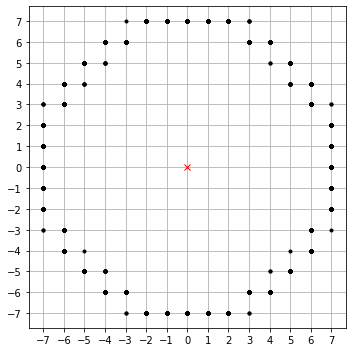
move on a grid
Each step you smell if you did a good move

finite memory
Put the reward far away
\(\Rightarrow\) 2 arms bandit problem
bandit problem
- N past (actions + reward)
- Shift Register of N bits
- Random Access Memory of N bits
Our agent will remember
bandit problem
with finite memory
Our approach to find an optimal strategy to the finite memory 2 arm bandit problem
environment \(\epsilon\)
- microstate : \(\sigma \in \Omega_\epsilon\)
- actions : \(a\)
- transition : \(P_\epsilon[\sigma_{t+1} | \sigma_t, a_t]\)
agent \(\pi\)
- state : \(s\)
- strategy : \(\pi(a,s)\)
\(s\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
\(\sigma\)
environment \(\epsilon\)
- microstate : \(\sigma \in \Omega_\epsilon\)
- actions : \(a\)
- transition : \(P_\epsilon[\sigma_{t+1} | \sigma_t, a_t]\)
agent \(\pi\)
- state : \(s\)
- strategy : \(\pi(a,s)\)
- \(P_\epsilon[s_{t+1}|s_t a_t \; s_{t-1} a_{t-1} \; \dots \sigma_0]\)
- \(= P_\epsilon[s_{t+1}|s_t a_t]\)
- \(P_{\epsilon\pi}[s'|s] = \sum_a \pi(a,s) P_\epsilon[s'|s a]\)
-
steady state: \(p_{\epsilon\pi}(s)\) power method
-
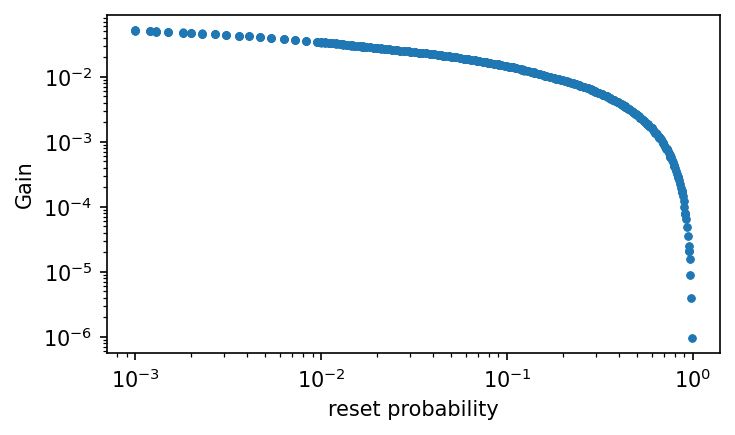
\(G = \langle\;\mathbb{E}_{\epsilon\pi}[r(s)]\;\rangle_\epsilon\)
-
gradient descent on \(\pi\)
problem of \(\infty\) time
finite time
\(\tilde P_\epsilon[\sigma' | \sigma, a]=(1-r) P_\epsilon[\sigma' | \sigma, a] + r \; p_0(\sigma')\)
reset probability : \(r\)
\( \langle \;\; \rangle_\epsilon, r \Rightarrow \pi \)
\(\epsilon = (\frac12 \leftrightarrow \frac12 \pm \gamma)\) and \(r = 10^{-9}\)
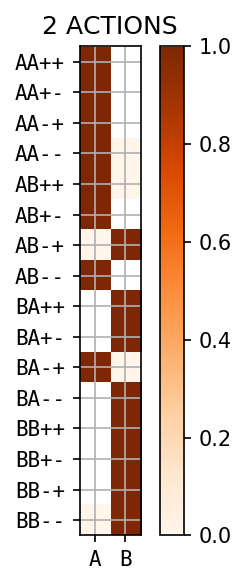
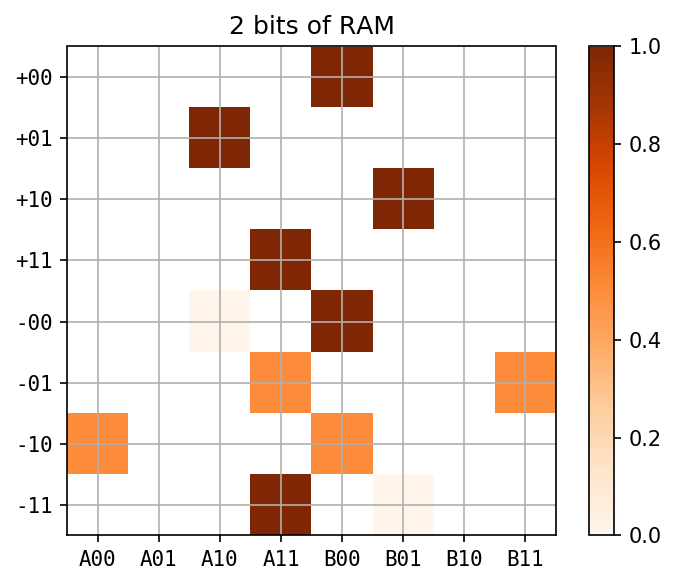
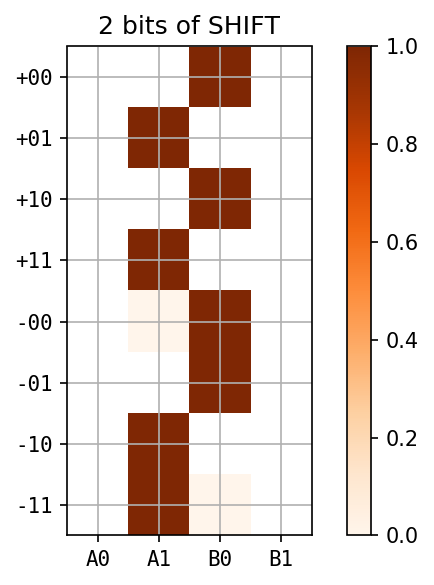
new action on the right
small probabilities \(\varepsilon\)
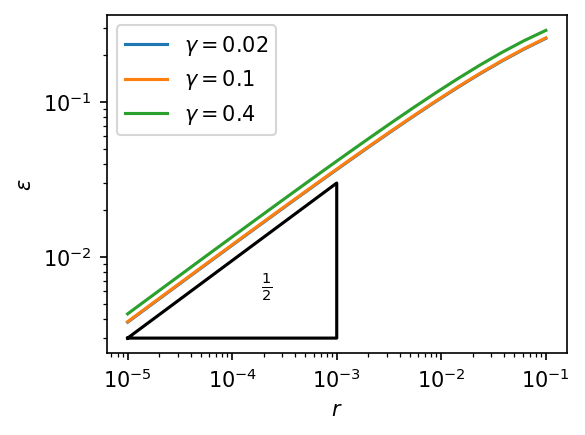
\(\varepsilon \propto \sqrt{r} \)
\(\text{expl. time} \propto \sqrt{\text{env. time}} \)

\(\varepsilon \propto \sqrt{r} \)
\(\text{expl. time} \propto \sqrt{\text{env. time}} \)
minimize \( t + T/t \)
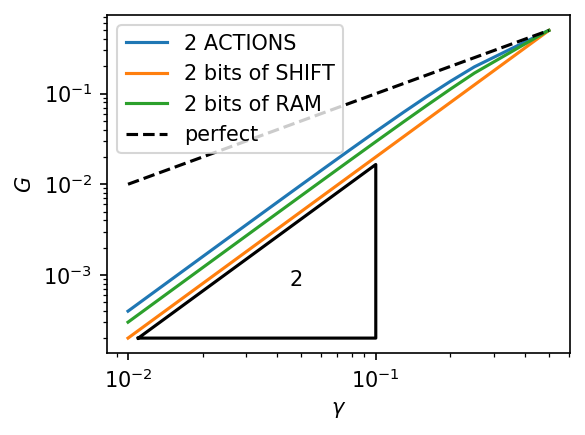
\(\epsilon = (\frac12 \leftrightarrow \frac12 \pm \gamma)\) and \(r = 10^{-9}\)
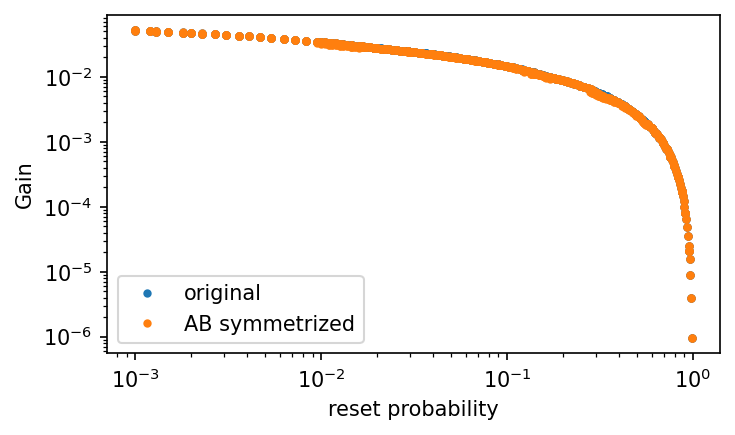
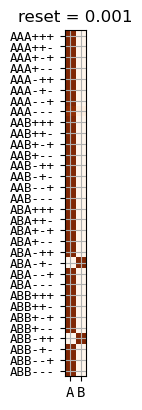
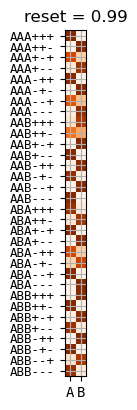
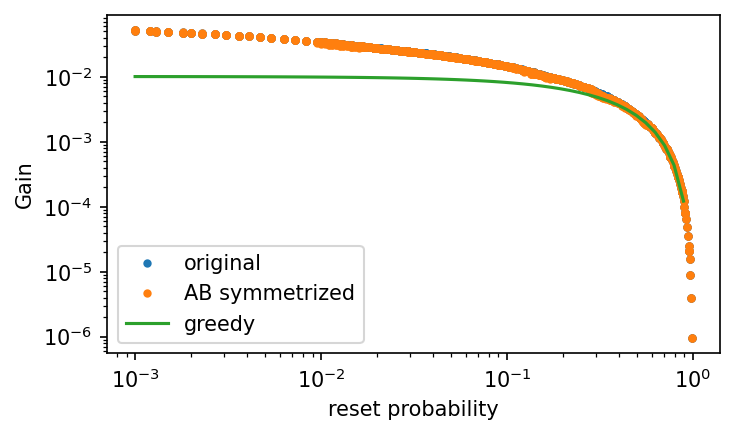
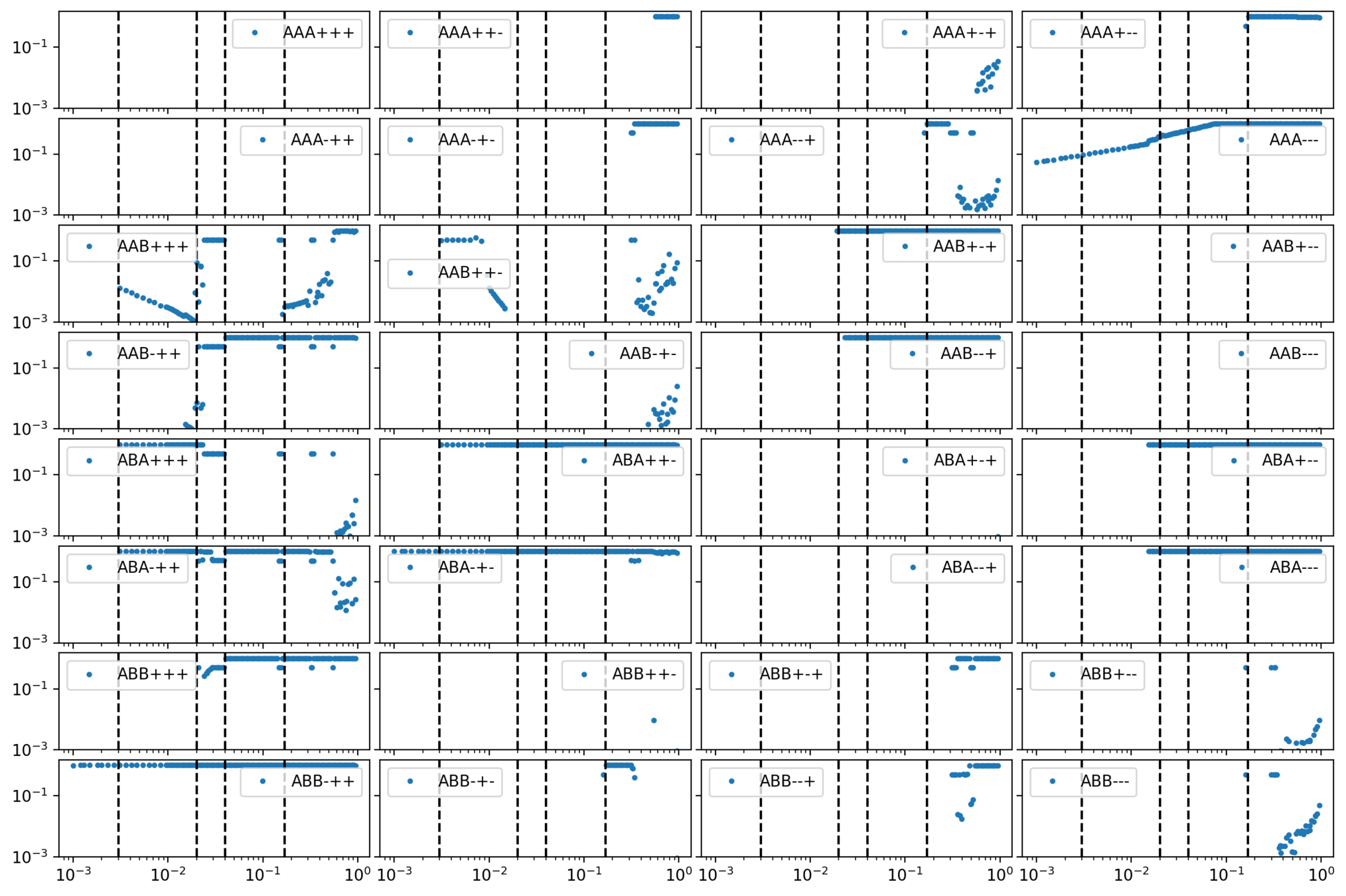

small reset
symmetric under \(A \leftrightarrow B\)
\(\epsilon = \sqrt{3r}\)
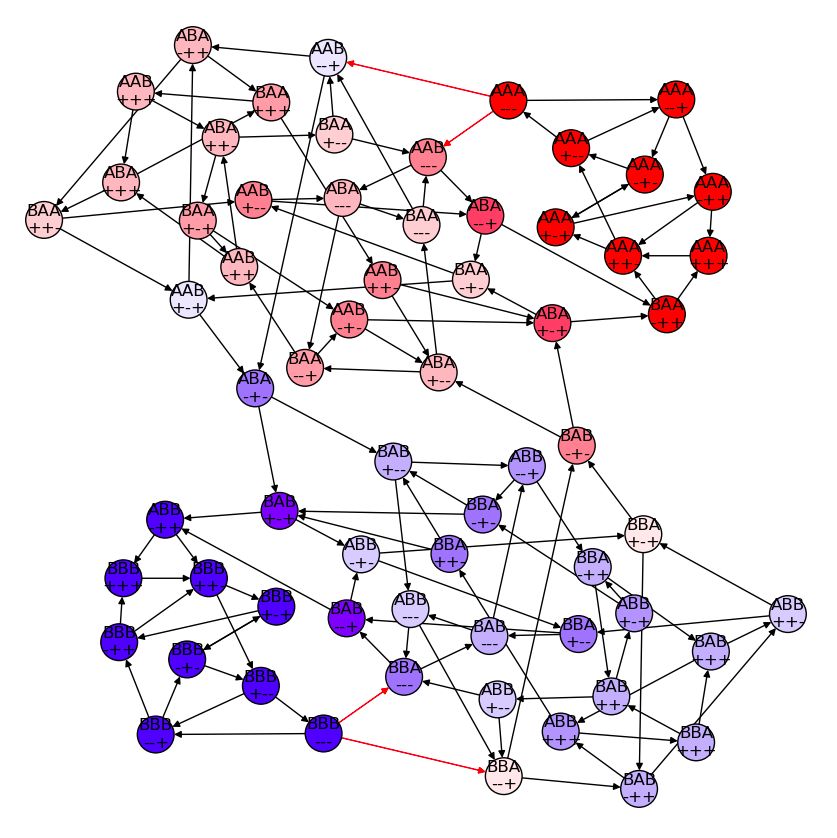

reset = 0.01
\(\epsilon \approx \sqrt{3r}\)
12 states out
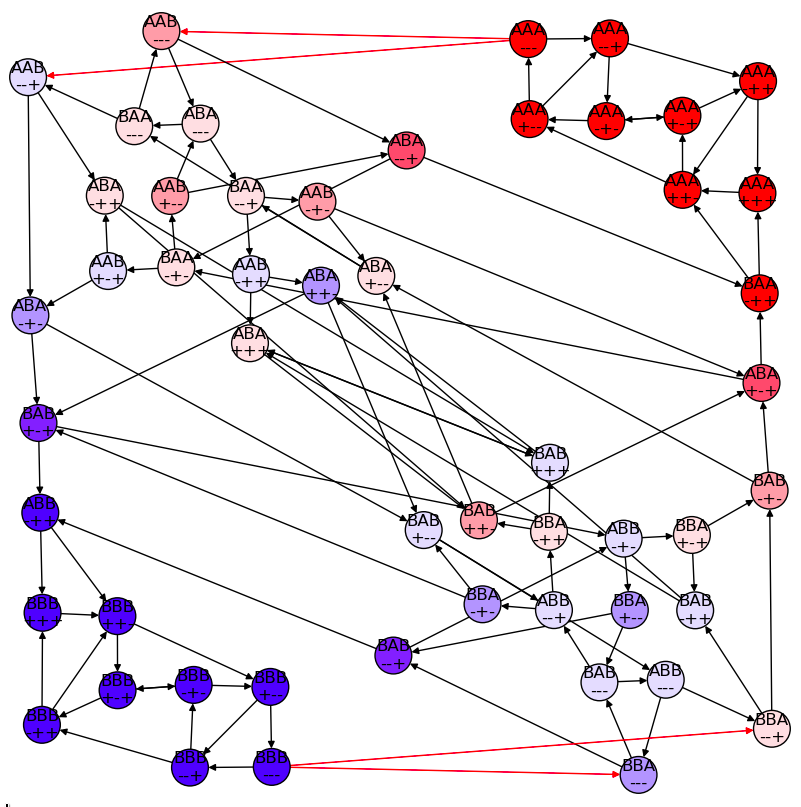
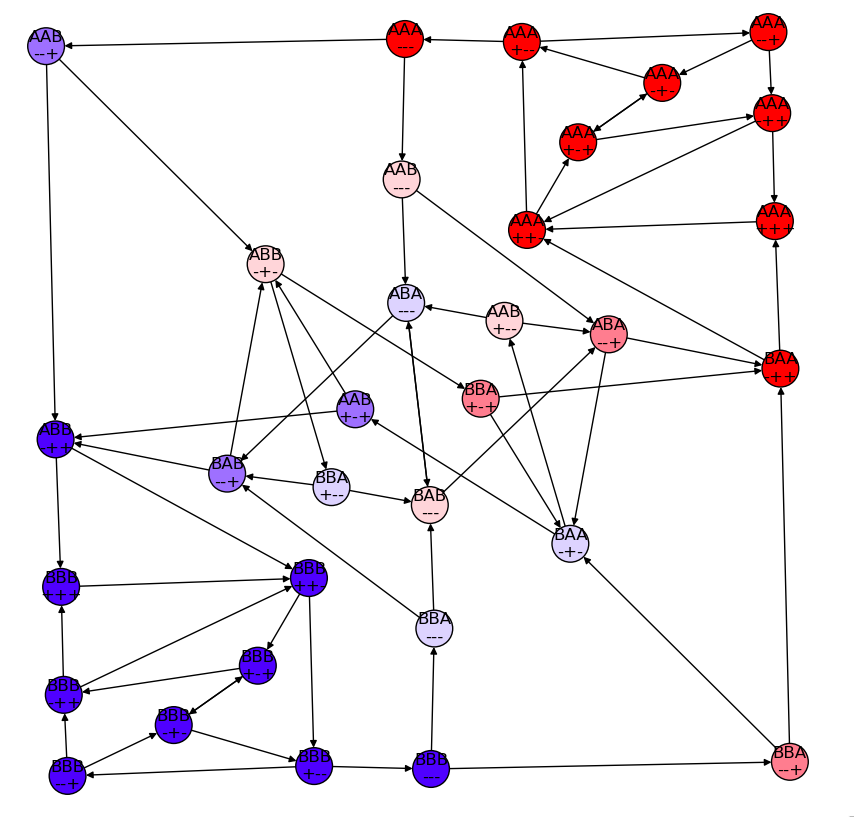
\(\pi\) at reset = \(0.1\)
\(p(s)=0\) for 32 states
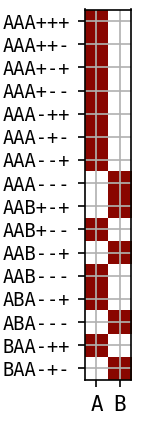
AAB+++ AAB++- AAB-++ AAB-+- ABA+++ ABA++- ABA+-+ ABA+-- ABA-++ ABA-+- ABB+++ ABB++- ABB+-+ ABB+-- ABB--+ ABB--- BAA+++ BAA++- BAA+-+ BAA+-- BAA--+ BAA--- BAB+++ BAB++- BAB+-+ BAB+-- BAB-++ BAB-+- BBA+++ BBA++- BBA-++ BBA-+-
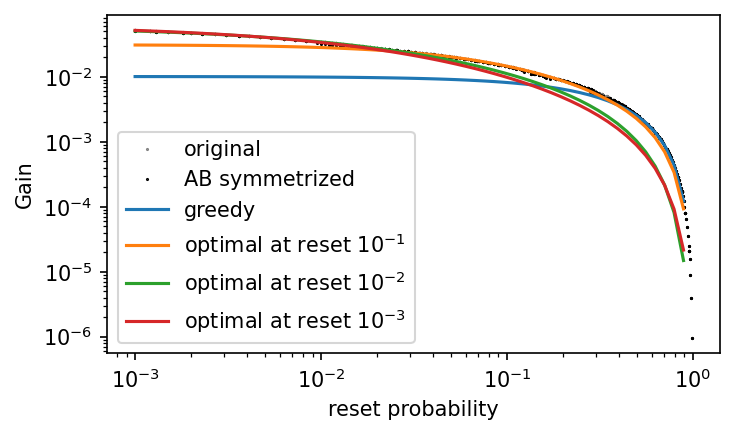
Thanks
Conclusions
Optimal solutions exploit best arm


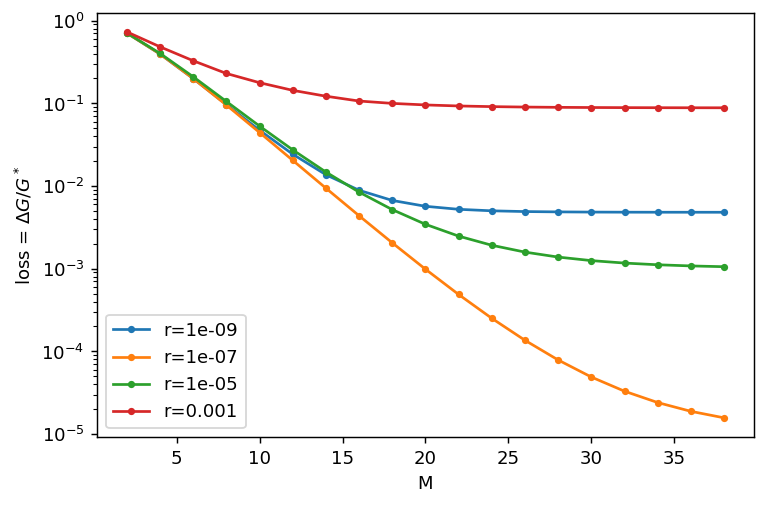
\(\Delta G/ G^* = 0.046 \rightarrow 0.045\)
reset \(r = 10^{-7}\)


\(\Delta G/ G^* = 0.045\)
gradient flow


\(\Delta G/G^* = 0.99 \rightarrow 0.005\)


reset \(r = 10^{-7}\)
\(G^* - G = 0.0005\)


reset \(r = 10^{-7}\)
\(G^* - G = 0.0006\)
U shape strat
\(\Delta G/G^* = 0.00098\)

random init
\(\Delta G / G^* = 0.00305\)
Determinist strat
\(\Delta G/G^* = 0.044 \)