Structured reasoning about actor systems

Leonardo Angel - Mateo Sanabria Ardila

Actors have unique identifiers and communicate via asynchronous message passing.

In response to a message, an actor may change its internal state, create new actors with a specified behavior (including an initial state), and/or send messages to known actors.

An actor configuration represents the potentially distributed state of a system at a single logical point in time.

Actors in a nutshell

The actor model imposes fairness on computation sequences in order to be valid.

Fairness: if a transition (from an actor configuration) is infinitely often enabled, the transition must eventually happen.

Actors properties

“if a process makes a print request infinitely often, then printing for that process will occur infinitely often”

The unbounded nondeterminism property means that messages are eventually received but there is no bound assumed on how many transitions may take place beforehand

Actors properties

Actors example

Ticker: repeatedly sends tick messages to Clock

Clock: Upon receipt of each tick increments an internal counter representing a time value

Ticker’s behavior keeps going by:

```
sending a continue message to itself 
```
```
Sending a tick message to Clock
```
```
Receiving the continue message       
```

Thus repeatedly moving through a sequence of three control states.

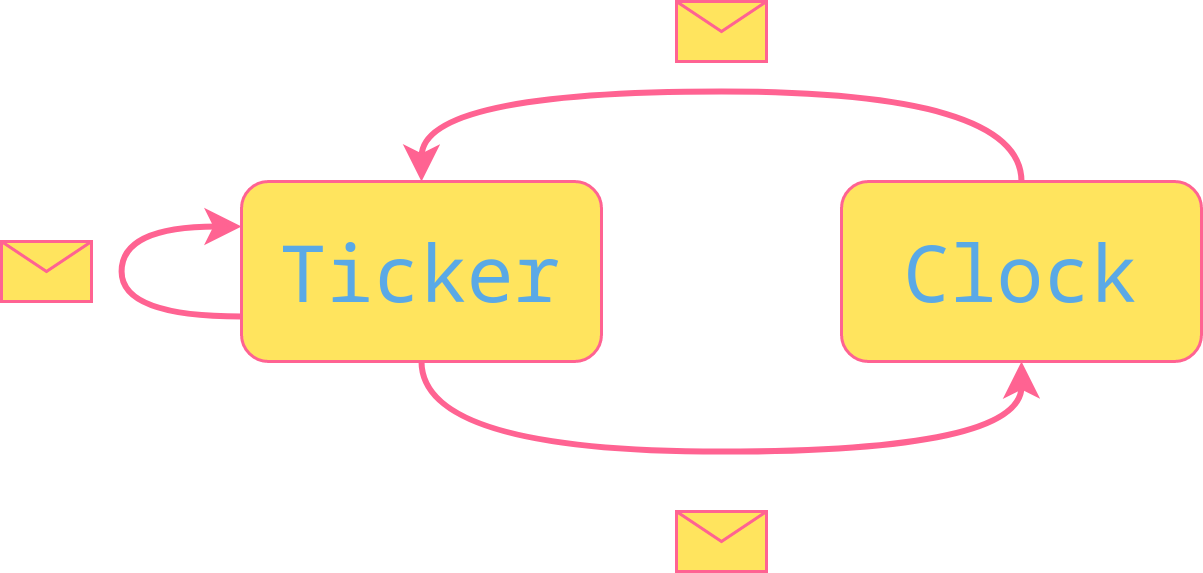
Unbounded nondeterminism: The property whereby the clock may wait an arbitrarily long time (as measured by the number of accumulated ticks) to receive a tick, but eventually it does and therefore makes progress in incrementing its own time value

actors properties within the example

Notice that without fairness, the ticker could keep producing tick messages indefinitely without any of them being received by the clock

About Athena implementation

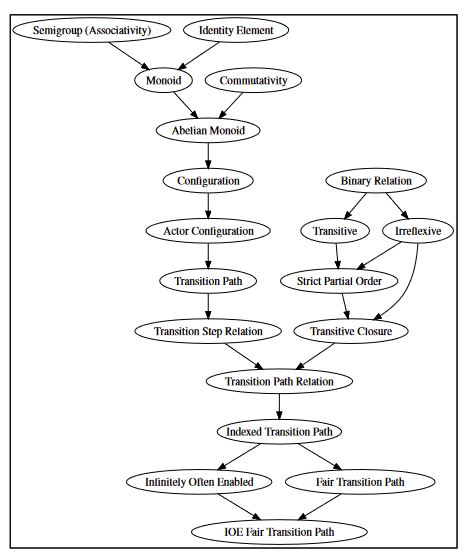
Athena implementation: Configuration

An actor configuration represents the potentially distributed state of a system at a single logical point in time

structure ( Cfg T ) :=
Null | ( One T ) | (++ ( Cfg T ) ( Cfg T ))

Null and ++ are axiomatized to form an Abelian Monoid. Null is the Monoid identity element for the binary ++ operator, which is associativeand and commutative

Athena implementation: Configuration

There are several theorems related to the configuration's behavior

Athena implementation: actors configuration

datatype ( Actor Id LS ) :=
( actor’ Id LS ) | ( message’ Id LS Id Ide )

define actor :=
lambda ( id ls ) ( One ( actor’ id ls ))

define message :=
lambda ( fr to c ) ( One ( message’ fr LS0 to c )

Athena implementation: actors configuration

s ++ (actor Ticker ( ticker local3 ))
  ++ (actor Clock ( clock local zero ))
  ++ (message Ticker Ticker’ continue )
  ++ (message Ticker Clock’ tick)

Athena implementation: actors transitions

Transition-Path datatype describe how configurations change in response to transition steps:

```
Message receiving
```
```
Message sending  
```
```
Actor creation steps
```

Athena implementation: actors transitions

datatype ( Step Id ) :=
( receive Id Id Ide )
| ( send Id Id Ide )
| ( create Id Id )

datatype ( TP Id LS ) :=
Initial
| ( then ( TP Id LS ) ( Step Id ))

declare config :
( Id , LS ) [( TP Id LS )] - > ( Cfg ( Actor Id LS ))

Athena implementation: actors transitions

declare ready-to :
( Id , LS ) [ LS ( Step Id )] - > Boolean

declare next :
( Id , LS ) [ LS ( Step Id )] - > LS

Athena implementation: Unique ids

 declare unique-ids: (Id, LS)
                     [(Cfg (Actor Id LS))] -> Boolean

 module unique-ids {
 define definition :=
  (forall s . (unique-ids s) <==>
              forall id . (count id s) <= one)
 }

aTHENA IMPLEMENTATION: Local states of ticker

local1: it's ready to send a 'continue message
local2: it's ready to send 'tick message to clock
local3: it's ready to recevice a continue message and continue to local1

Athena implementation: actors transitions

T1 = ( T0 then ( receive Clock Ticker ’tick))

config T1 =
s ++ (actor Ticker ( ticker local3 ))
  ++(actor Clock ( clock local ( S zero )))
  ++(message Ticker Ticker’ continue)

PATH example

define P :=
  ( Initial then (create Clock Ticker)
            then (send Ticker Ticker ’continue)
            then (send Ticker Clock ’tick)
            then (receive Clock Ticker ’tick)
            then (receive Ticker Ticker ’continue)
            then (send Ticker Ticker ’continue)
            then (send Ticker Clock ’tick)
            then (receive Ticker Ticker ’continue)
            then (send Ticker Ticker ’continue)
            then (send Ticker Clock ’tick)
            then (receive Clock Ticker ’tick))

Conclusions

Absence of linear sequences in transitions may lead to explosion of potential paths.
A hierarchy of well-defined theories allows to lower the complexity of theorems.

Critique AND future research

\forall_y \square ( print\_request(y) \Rightarrow \lozenge printed(y) )

```
Complexity of example (Clock-Ticker)
```
```
Relation between steps on paths
```
```
Temporal Logic articulateness
```

Discussion

Questions