Busqueda en grafos

Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Definicion

Un grafo G = (V,E), es una pareja ordenada en la que V es un conjunto no vacío de Vértices y E un conjunto de Aristas

Por QUÉ grafos en CS?

```
Redes de computadores
```
```
Redes sociales
```
```
Circuitos
```
```
Demostración de teoremas
```
```
Recolector de basura
```
```
Resolver puzzles
```
```
...
```

Que tan grande puede ser un grafo?

|E| \leq 2 \cdot | V \times V | = \mathcal{O}(|V|^2)

|E| \leq | V \times V | = \mathcal{O}(|V|^2)

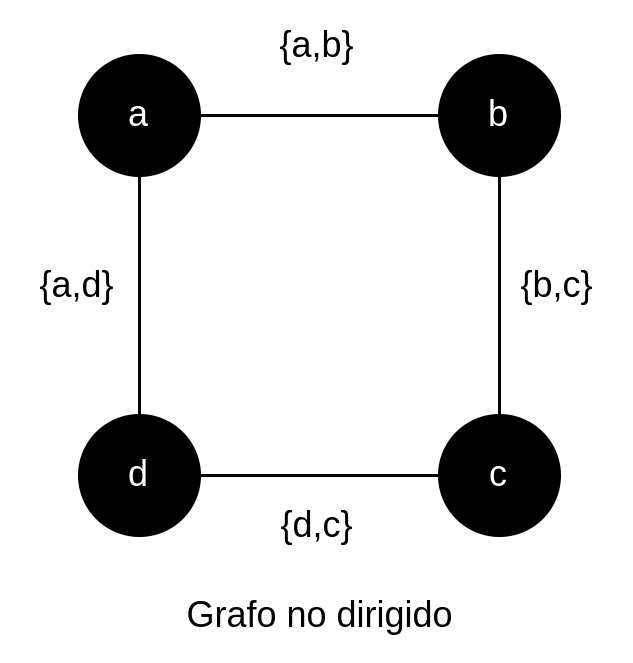
Grafo no dirigido

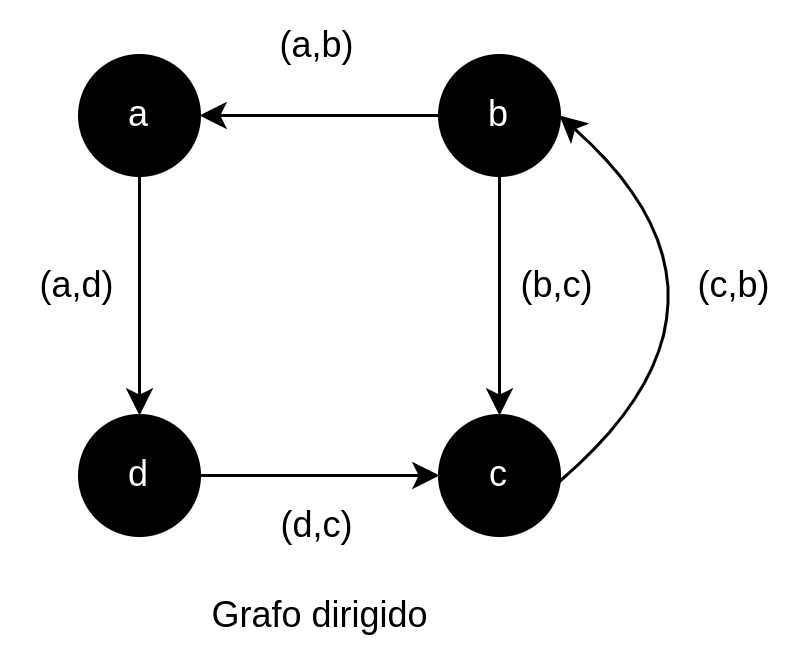
Grafo dirigido

Representación de grafos

```
Matriz de adyacencia
```
```
Lista de adyacencia
```
```
Lista de aristas
```

Caminos (pathS)

Un camino p es secuencia de vértices tales que :

\small p = (v_1,\cdots,v_k) \ tal \ que \ (v_i,v_{i+1}) \in E

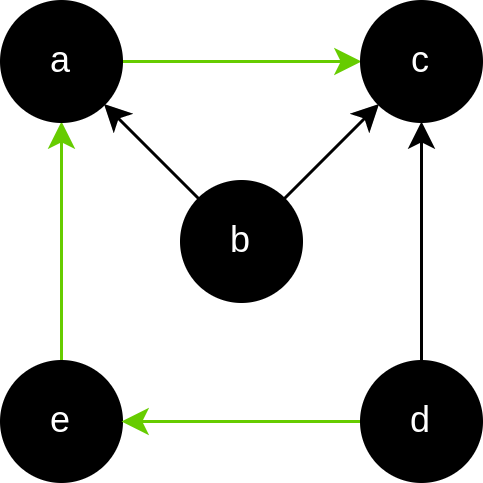
\tiny p = (d,e,a,c)

\tiny l(p) := longitud \ de \ p

\tiny \delta(d,c) := longitud \ camino\ mas \ corto \ d \ , \ c

Problemas sobre grafos

Dado un grafo G=(V,E) y dos vertices v,w 
se quiere saber:

Existe algún camino que conecte a v y w en el grafo G?

Cual es el camino de menor longitud que comunica a v,w en el grafo G?

Cuales son los caminos más cortos entre un v y todos los demás vértices en el grafo G?

Note que para los problemas definidos anteriormente puede ser importante almacenar el camino con menor longitud entre dos nodos de un grafo G, como se puede hacer eso?

Breadth-first search (bfs)

Li(s):= conjunto de vertices alcanzables desde s usando un camino más corto de longitud i (nivel i de s)

Dado un grafo G y un vértice v BFS encuentra todos niveles del vértice v

# Adj: Lista de adjacencia
# s : int
def bfs(Adj, s): 
 visited = [False for v in Adj] 
 queue = [s]
 while 0 < len(queue): 
   current_node = queue.pop(0)
   if not visted[current_nod]:
    # Usually here you do something 
    # with the current node
    visted[current_nod] = True
    for n in Adj[current_node]:
      if not visited[n]:
        queue.append(n)

Flood fill problem

Problemas sobre grafos

```
Detección de ciclos
```
```
Componentes conectos
```

Clasificación de aristas (Tree,Back,Forward,Cross)

```
Ordenes topológicos
```

Depth-first search (Dfs)

La estrategia de DFS consiste en buscar "más profundo" en el grafo siempre que sea posible.

Explora las aristas que salen del vértice descubierto más recientemente y que aún tiene aristas sin explorar.

Una vez exploradas todas las aristas, "retrocede" para explorar aristas que salgan del vértice desde el que se descubrió.

Este proceso continúa hasta que se descruba todos los vértices alcanzables desde el vértice de origen.

# Adj: Lista de adjacencia
# s : int
# visted = [False for v in Adj]  
def dfs(Adj, s, visited): 
  # Usually here you do something 
  # with the current node 
  visted[s] = True
  for n in Adj[s]:
    if not visited[n]:
      dfs(Adj,n,visited)

Un grafo no dirigido G es un árbol sii es conecto y no tiene ciclos

Gafros: arboles

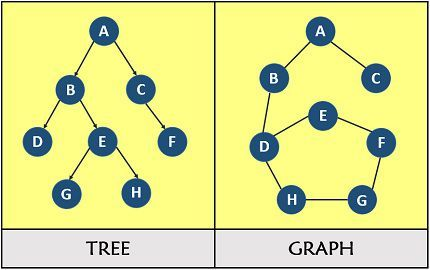
dado un grafo G, como se utiliza DFS para validar que sea un arbol?

econtrar caminos mas cortos en grafos cargados

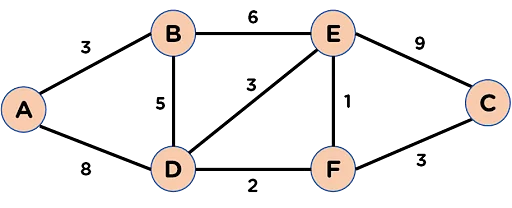
Algoritmo del camino más corto de Dijkstra

Algoritmo del camino más corto de Bellman-Ford

Single source shortest paths

Board Time!