Athena-LTL

Leonardo Angel - Mateo Sanabria A

1

LTL overview

2

Syntax and operational semantics of Athena’s core language

3

Athena’s core changes

Linear Temporal Logic (LTL)

#LTL

Commonly, propositional, discrete, linear temporal logic extends the descriptive power of propositional logic in order to be able to describe sequences of distinct worlds, with each world being similar to a classical model.

In the next moment in time, ‘running’ will be true and, at some time after that, ‘terminated ’ will be true.

Linear Temporal Logic: Syntax

#LTL
\bigcirc \phi := \small{\phi \text{ is true in the next moment in time}}
\square \phi :=\small{ \phi \text{ is true in all future moments}}
\lozenge \phi := \small{ \phi \text{ is true in some future moment}}

In LTL, as well as classical propositional operators, we use temporal operators referring to moments in the future:

Linear Temporal Logic: Syntax

#LTL

"It is always the case that, if either ‘have_passport’ or ‘have_ticket’ is false, then, in the next moment in time ‘board _flight’ will also be false"

\small \square(\ \neg have\_passaport \ \vee \ \neg have\_ticket \\ \rightarrow \\ \bigcirc\neg board\_flight \ )

Linear Temporal Logic: Semantics

#LTL

Models for temporal  logics are typically ‘Kripke Structures’ of the form:

 

\mathcal{M} = < S,R,\pi >
  • S is the set of moments in time
  • R is a temporal accessibility relation
  • π : S → P maps each moment/world/state to a set of propositions. Those that are true in that moment/world/state.

Linear Temporal Logic: Semantics

#LTL

Models for temporal  logics are typically ‘Kripke Structures’ of the form:

 

\mathcal{M} = < \mathbb{N},\pi >
  • S is the set of natural numbers
  • π : N → P maps each Natural Number (representing a moment in time) to the set of propositions true at that moment.

Linear Temporal Logic: Semantics

#LTL
\mathcal{M} = < \mathbb{N} ,\pi >

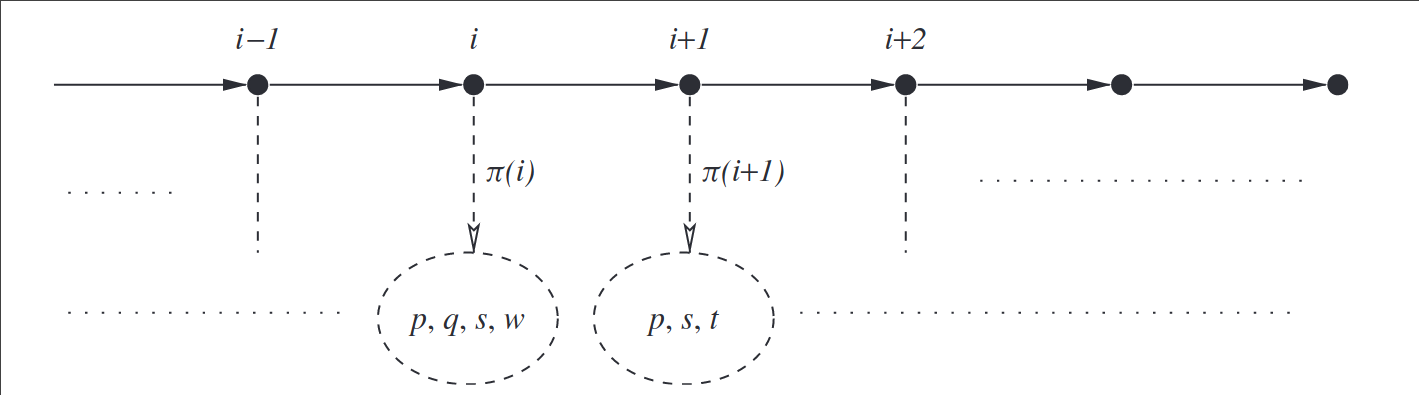
Linear Temporal Logic: Semantics

#LTL

The semantics of the standard classical operators is as expected

\tiny <\mathcal{M},i> \models \neg \phi \ \text{ iff is not the case that} <\mathcal{M},i> \models \phi
\tiny <\mathcal{M},i> \models \phi \wedge \tau \ \text{ iff both } <\mathcal{M},i> \models \phi \ \text{ and } \ <\mathcal{M},i> \models \tau
\tiny <\mathcal{M},i> \models \phi \ \vee \ \tau \ \text{ iff } \ <\mathcal{M},i> \models \phi \ \text{ or } <\mathcal{M},i> \models \tau
\tiny <\mathcal{M},i> \models \phi \ \rightarrow \ \tau \ \text{ iff if } \ <\mathcal{M},i> \models \phi \ \text{ then } <\mathcal{M},i> \models \tau
\tiny <\mathcal{M},i> \models p \ \text{ iff } p \in \pi(i)

Linear Temporal Logic: Semantics

#LTL

The ‘next’ operator provides a constraint on the next moment in time

\tiny <\mathcal{M},i> \models \bigcirc \phi \ \text{ iff } <\mathcal{M},i+1> \models \phi

Linear Temporal Logic: Semantics

#LTL

 The ‘eventually’ operator  describes a constraint on the future. We can be sure that φ will be true either now or in the future, we can not be sure exactly when it will become true

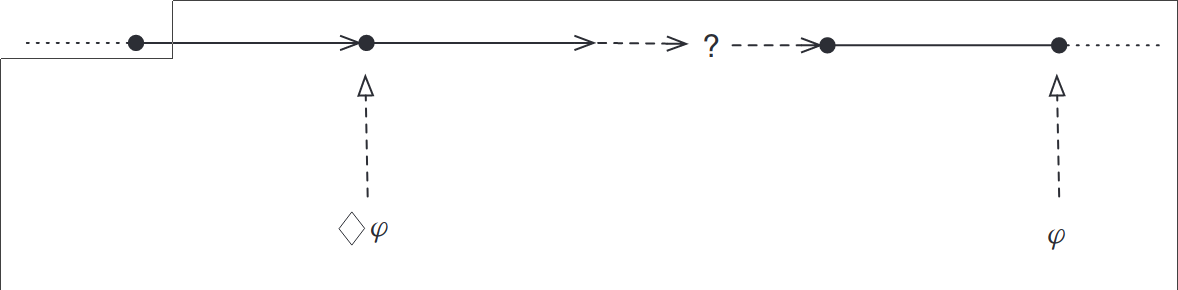
\tiny <\mathcal{M},i> \models \lozenge \phi \ \text{ iff } (\exists j| i \leq j : \ <\mathcal{M},j> \models \phi)

Linear Temporal Logic: Semantics

#LTL

The ‘always in the future’ operator, provides  the ability to represent invariant properties, that is properties that are true at all moments in time from now on

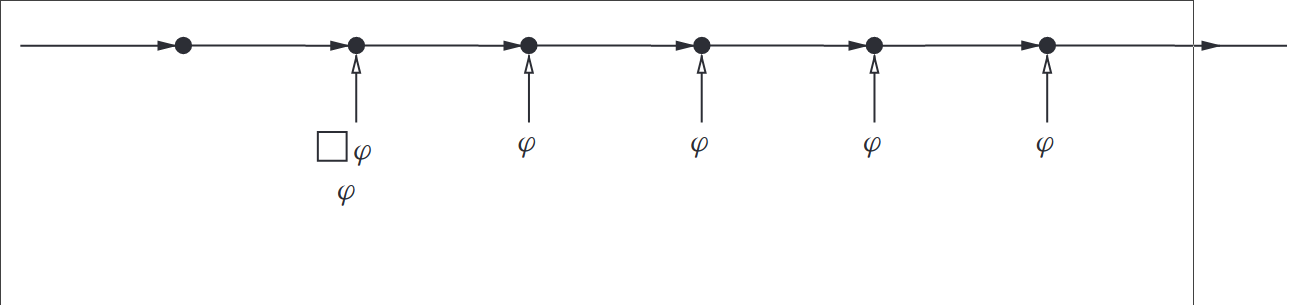
\tiny <\mathcal{M},i> \models \square \phi \ \text{ iff } (\forall j| i \leq j : \ <\mathcal{M},j> \models \phi)

Linear Temporal Logic: Semantics

#LTL

Notice that the value of a proposition depends on the model and the moment:

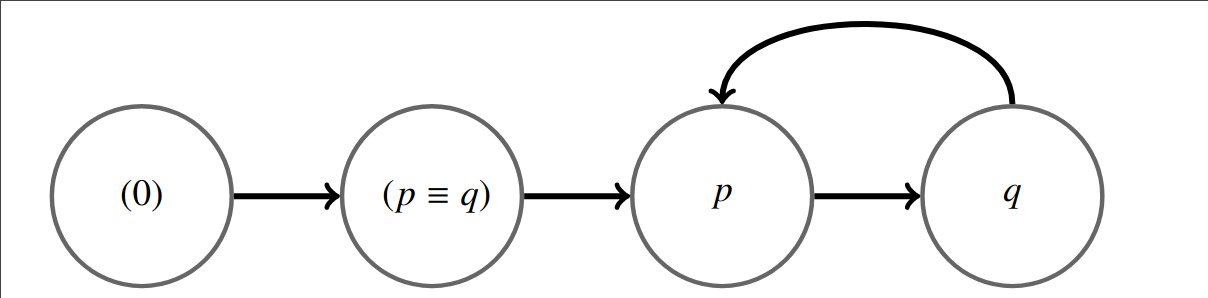
Linear Temporal Logic: Semantics

#LTL

Yet there are LTL formulas that are valid for every model at every moment:

\models \square(\phi \rightarrow \tau) \rightarrow (\square \phi \rightarrow \square\tau)
\models \square \neg \phi \equiv \neg\lozenge \phi

Athena Operational semantics

#Athena

Why?!

We want to implement LTL inside the Athena base core: Athena-LTL

Athena: Operational semantics

  • An environment ρ is a computable function that maps any given identifier I either to a value V or to a special unbound token.
  • An assumption base β is a finite set of sentences.
  • A store σ is a computable function that maps any natural number (representing a memory location) to a value (the location’s contents).
  • A symbol set γ is a collection of function symbols and their respective signatures, along with a collection of sort constructors and their arities; γ also includes information on whether a given sort constructor is a datatype or structure, and if so, which function symbols are its constructors.
#Athena

Athena: Operational semantics

Athena's operational deductions for expressions is huge!

#Athena

Athena: Operational semantics

#Athena
\mathbf{method} \ (I_1 \cdots I_E) \ D

The value of the method in ρ, β, σ, and γ is a method value that takes a list of n values V1 , . . . , Vn along with an assumption base β´and store σ´as arguments, and produces the result of evaluating the deduction D in

\rho [I_1 \rightarrow V_1 \cdots I_n \rightarrow V_n], \beta', \alpha', \gamma

Athena: Operational semantics

The result of evaluating a phrase F with respect to given ρ, β, σ, and γ, is one of three things:

  • A pair (V, σ´) consisting of a value V and a store σ,́ where V is the output of the evaluation and σ´reflects any side effects accumulated during the evaluation
  • A pair consisting of an error message and a store σ,́ indicating the occurrence of an error during the computation
  • Nontermination.
#Athena

Athena's core changes

#Changes

On top of Athena's first order logic implementation, we would aim to add the necessary axioms and properties in order to be able to reason about LTL on Athena. 

\models \square \neg \phi \equiv \neg\lozenge \phi
(!equiv (!Always ~ ?phi) ~(!Eventually ?phi))​

Athena's core changes

One interesting definition we might consider useful could be Invariant, a property that does not change over time.

\footnotesize (\forall i | t_1 \leq i \leq t_2: <\mathcal{M},i> \models \phi \equiv \neg \omega \lor \tau)

If invariants are restricted to specific time intervals, LTL can be seen as a succesion of invariants over variable time periods.

#Changes
  • Propose a full definition for the Athena-LTL operational semantic
  • Understand/Update the current Athena implementation to achieve Athena-LTL