algorithm complexity Basic concepts

Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

def has_sqrt(number: int) -> bool:
    result = False
    for i in range(1, number):
        if i * i == number:
            result = True
    return result


def has_sqrt_list_0(i_list: list[int]) -> list[int]:
    result = []
    for k in i_list:
        if has_sqrt(k):
            result.append(k)
    return result


def has_sqrt_list_1(i_list: list[int]) -> list[int]:
    flag = True
    i, count = 0, 0
    _len = len(i_list)
    while count < _len:
        if not has_sqrt(i_list[count - i]):
            i_list.pop(count - i)
            i += 1
        count += 1
    return i_lis

Cual es mejor?

Existen restricciones que se deben tener en cuenta cuando se diseñan algoritmos:

```
La capacidad de memoria
```
```
El tiempo de ejecución del algoritmo
```
```
Los costos operacionales
```

La maquina donde se ejecutara el algoritmo

```
...
```

Se quiere un método de comparación independiente del hardware y del lenguaje de programación

has_sqrt_list_0

has_sqrt_list_1

Tamaño de la entrada: Depende del problema...

```
Lista: longitud de la lista
```
```
Entero: cantidad de bits
```
```
Grafo: ? 
```

Tiempo de ejecución: Numero de operaciones primitivas(steps)ejecutadas

Cada linea de código toma una cantidad constante para ejecutarse.

Cada linea de código puede tener una cantidad de tiempo ejecución diferente.

T(n) <-> 'Tiempo' de ejecución para una entrada de tamaño n del algoritmo

def has_sqrt_list_0(i_list: list[int]) -> list[int]:
    result = []          
    for k in i_list:     
        if has_sqrt(k):
            result.append(k)
    return result

C1	asignacion
C2	iterador
C3	bool Op
C4	has_sqrt
C5	append list Op
C6	acceder a indice
C7	len list Op
C8	pop list Op

def has_sqrt_list_0(i_list: list[int]) -> list[int]:
    result = []          	 # T = C1
    for k in i_list:     	 # T = C2 + n * C6
        if has_sqrt(k):  	 # T = n * (C3 + C4(k))
            result.append(k) # T = n * C5
    return result

T_0(n) = C1 + C2 + nC6 + n(C3 +C4(k)) + nC5

C1	asignacion
C2	iterador
C3	bool Op
C4	has_sqrt
C5	append list Op
C6	acceder a indice
C7	len list Op
C8	pop list Op

def has_sqrt_list_1(i_list: list[int]) -> list[int]:
    flag = True                		# T = C1
    i, count = 0, 0            		# T = 2 * C1
    _len = len(i_list)         		# T = C7 + C1
    while count < _len:        		# T = n * C3 
        if not has_sqrt(i_list[count - i]):  
            # T = n * (C4 + C6 + C3)
            i_list.pop(count - i) 	# T = n * C8
            i += 1 # T = C1
        count += 1 # T = C1
    return i_lis

T_1(n) = ?

C1	asignacion
C2	iterador
C3	bool Op
C4	has_sqrt
C5	append list Op
C6	acceder a indice
C7	len list Op
C8	pop list Op

Se quiere un método de comparación independiente del hardware y del lenguaje de programación

has_sqrt_list_0

has_sqrt_list_1

T_1(n) =  6*C1 + C7 +  n(C4(k) + C6 + 2*C3 + C8)

T_0(n) = C1 + C2 + n(C3 + C4(k) + C5 + C6)

En realidad quisiéramos entender como crece el costo de ejecución con respecto al crecimiento de la entrada, sin la necesidad de constantes particulares.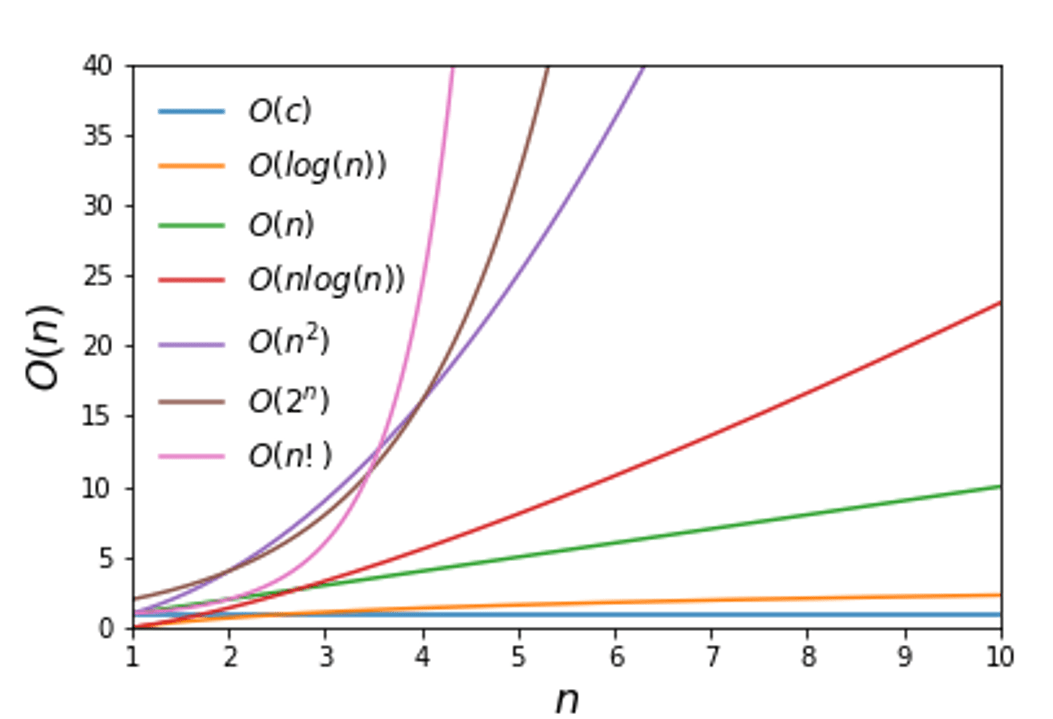

orden de complejidad

Sean  $f$  y  $g$  funciones con codominio en los naturales y rango en los reales positivos

```
 $f$  es de orden menor o igual que  $g$  sii
```

\small (\exists c,k \in \mathbb{N} \ |: (\forall m \in \mathbb{N} \ | \ k \leq m \ : f(m) \leq c g(m) ) )

```
y se escribe
```

f = \mathcal{O}(g)

f(n) = \mathcal{O}(g(n))

orden de complejidad

```
 $f$  es de orden igual que  $g$  sii
```

f = \mathcal{O}(g) \ \wedge \ g = \mathcal{O}(f)

```
y se escribe
```

f = \Theta(g)

f(n) = \Theta(g(n))

orden de complejidad

Como se comparan las siguientes funciones en terminos de orden de complejidad

f(n) = 10n \ \wedge \ g(n) = n^2 \\ f(n) = 10n^3 \ \wedge \ g(n) = 100n^2 \\ f(n) = 10n \ \wedge \ g(n) = 5n + 30 \\

orden de complejidad: teoremas

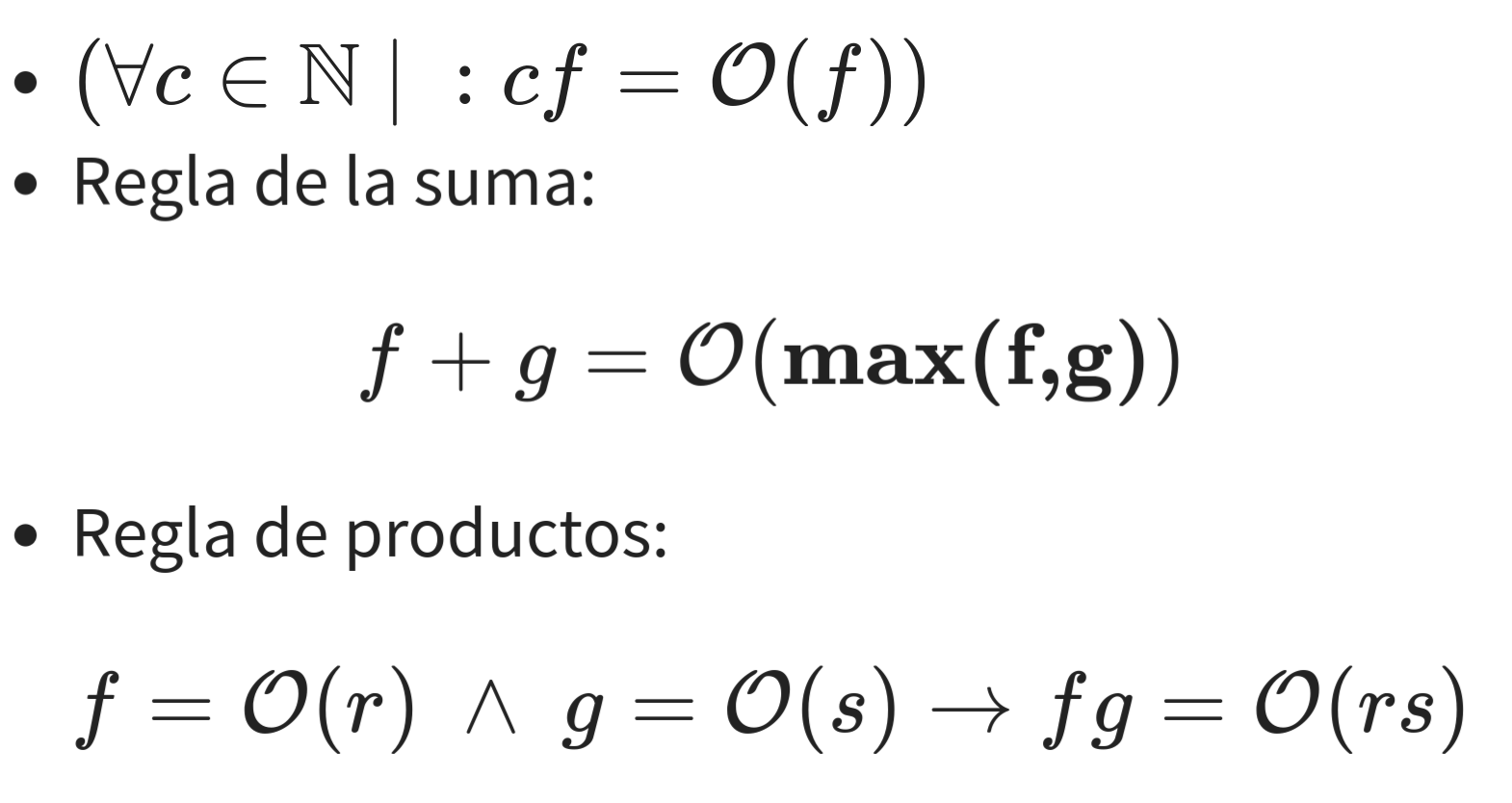
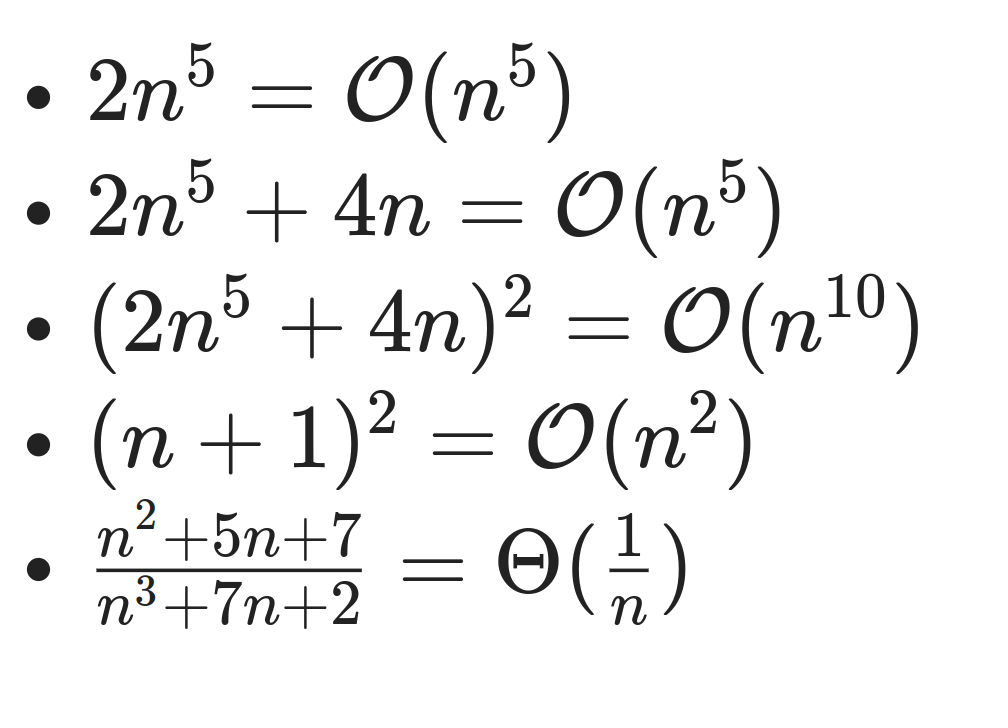
orden de complejidad: EJEMPLOS

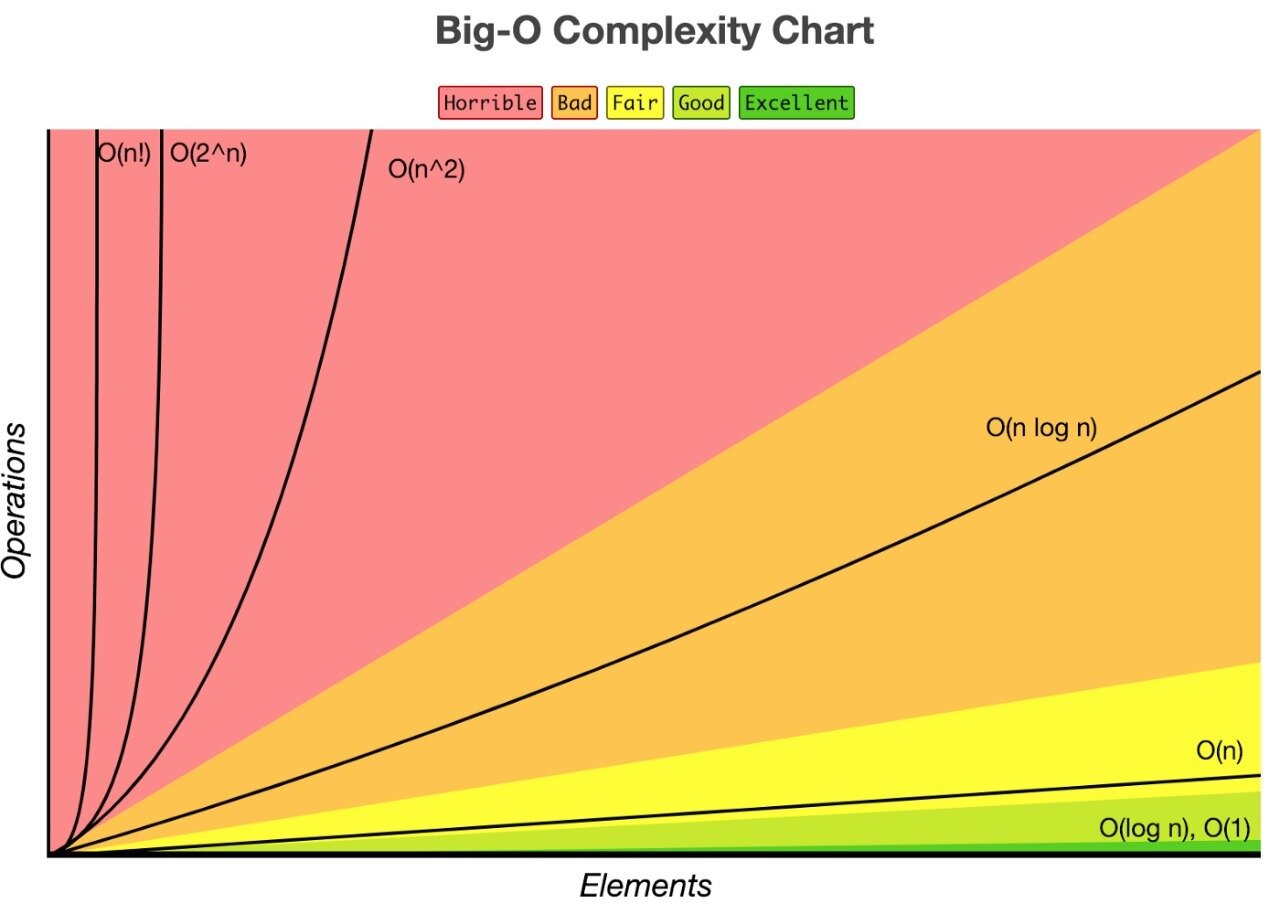
def busqueda_binaria(arreglo, busqueda, izquierda, derecha):
  if izquierda > derecha:
  	return -1
  middle_index = (izquierda + derecha) // 2
  middle_element = arreglo[middle]
  if middle_element == busqueda:
  	return middle_index
  if busqueda < elementoDelMedio:
  	return busqueda_binaria(arreglo, busqueda, izquierda, middle_index - 1)
  else:
  	return busqueda_binaria(arreglo, busqueda, middle_index + 1, derecha)