Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Algoritmos aproximados

Si cualquier problema NPC es soluble en tiempo polinomial entonces: P = NP
L_2 \in P \ \wedge \ L_1 \leq_P L_2 \rightarrow L_1 \in P
Todos los problemas NPC son solubles en tiempo polinomial.
 

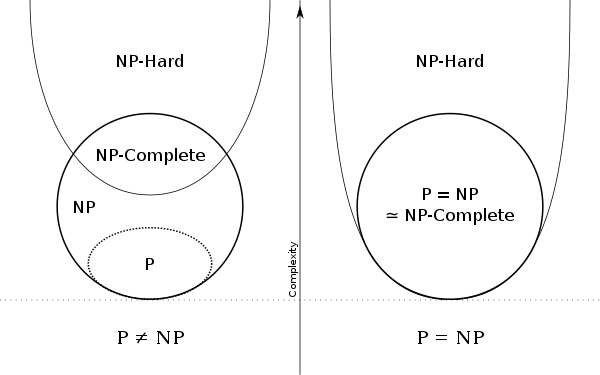
Even if a problem is NPC, there may be hope

  • Las entradas son suficientemente pequeñas para tener resultados con algoritmos exponenciales, en tiempos razonable.
  • Aislar casos que puedan ser solucionados en tiempo polinomial.

  • Encontrar soluciones aproximadas en tiempo polinomial.

vertex cover

Dado un grafo no dirigido G=(V,E) el problema consiste en encontrar V' como la minima cobertura de vertices para G
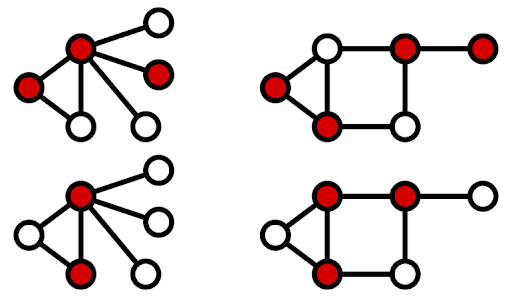
Approx-Vertex-Cover devuelve una cobertura de vertices que es como mucho 2 veces mas grandes que la cobertura optima.
Approx-Vertex-Cover es un 2-approximation algorithm

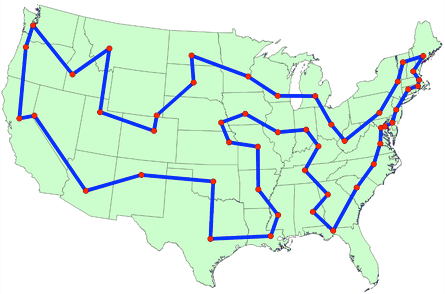
Traveling-salesman

Dado un grafo completo no dirigido G=(V,E) cargado, sin costos negativos. Se debe encontrar el ciclo Hamiltoniano de menor costo.
Una función de costo satisface la desigualdad triangular si para los nodos u,n,w se cumple
c(u,w) \leq c(u,n) + c(n,w)
Por ejemplo, si los nodos del grafo G representan puntos en el plano y la función de costo es la distancia euclidiana, la propiedad se cumple.

Approx-TSP-TOUR devuelve un ciclo hamiltoniano de G cuyo costo (dado c) es como mucho 2 veces mas grande que el ciclo hamiltoniano optimo.
Approx-TSP-TOUR  es un 2-approximation algorithm 
Una recorrido de un árbol en preorden, recorre recursivamente todos los nodos del árbol listando un nodo cuando se encuentra por primera vez antes de visitar sus hijos. Primero se recorre el sub-árbol izquierdo.
Que pasa si la función de costo no satisface la desigualdad triangular?
Si P  NP entonces no existe un algoritmo p aproximado para el problema general de TSP
\not =

Set-covering

X = \bigcup\limits_{c_i\in \ \mathcal{C}} c_i 
El tamaño de la cobertura es la cardinalidad de
\mathcal{C}
Sea X un conjunto y        se dice que   cubre a X si
\mathcal{C} \subseteq \mathcal{P}(X)
\mathcal{C}

Set-covering

SET-COVER = \{\langle X,\mathcal{F}, k \rangle : \\ (\exists C \subseteq \mathcal{F} \ | \ \text{C es una cobertura de X de tamaño k} ) \}

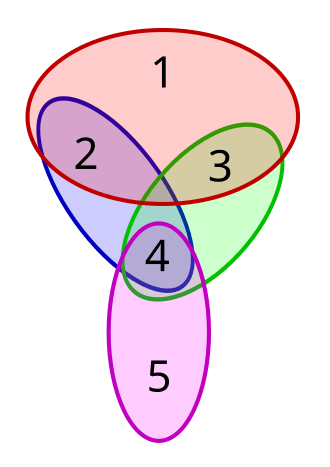
Set-covering

Problema de optimización: Dado X y  econtrar la cobertura   de tamaño minimo.
\mathcal{C}
\mathcal{F}

Set-covering es NPC

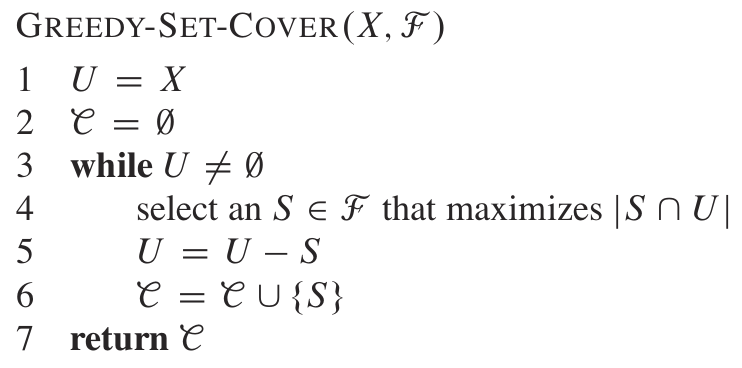
Approx-TSP-TOUR es un (ln|X|+1)-approximation algorithm