Análisis de flujo en redes
Mateo Sanabria Ardila
ISIS1105: Diseño y análisis de algoritmos

Contexto
Grafos dirigidos como representación de flujo de material en una 'red'
-
Material producido desde una 'fuente'
-
El material se necesita en un 'sink'
-
El material es producido a un ritmo x en la fuente y consumido a un ritmo y en el 'sink'
-
Existe una 'red' que comunica 'fuente' y 'sink'
-
Los nodos de la 'red' reciben el mismo ritmo que el ritmo que despachan
Cual es el mayor ritmo al que se puede despachar el material desde la 'fuente' al 'sink' dada una red particular?Material producido desde una 'fuente'

El material se necesita en un 'sink'

El material es producido a un ritmo x en la fuente y consumido a un ritmo y en el 'sink'

Existe una 'red' que comunica 'fuente' y 'sink'
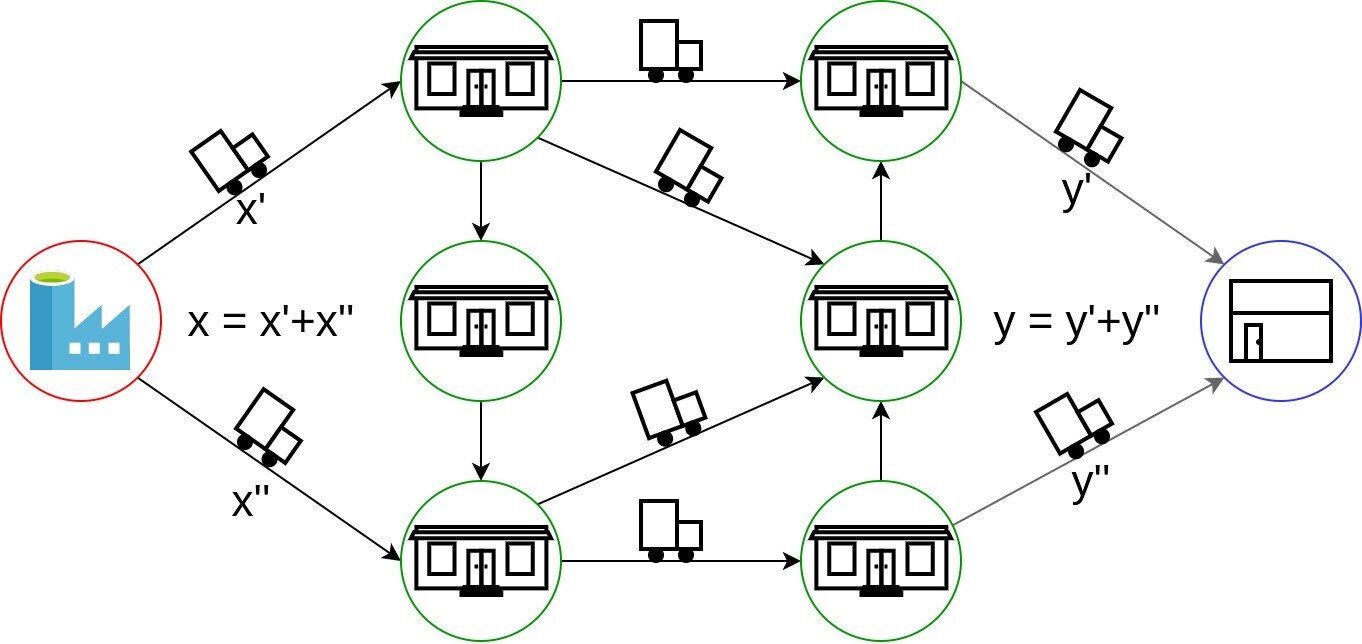
Los nodos de la 'red' reciben el mismo ritmo que el ritmo que despachan
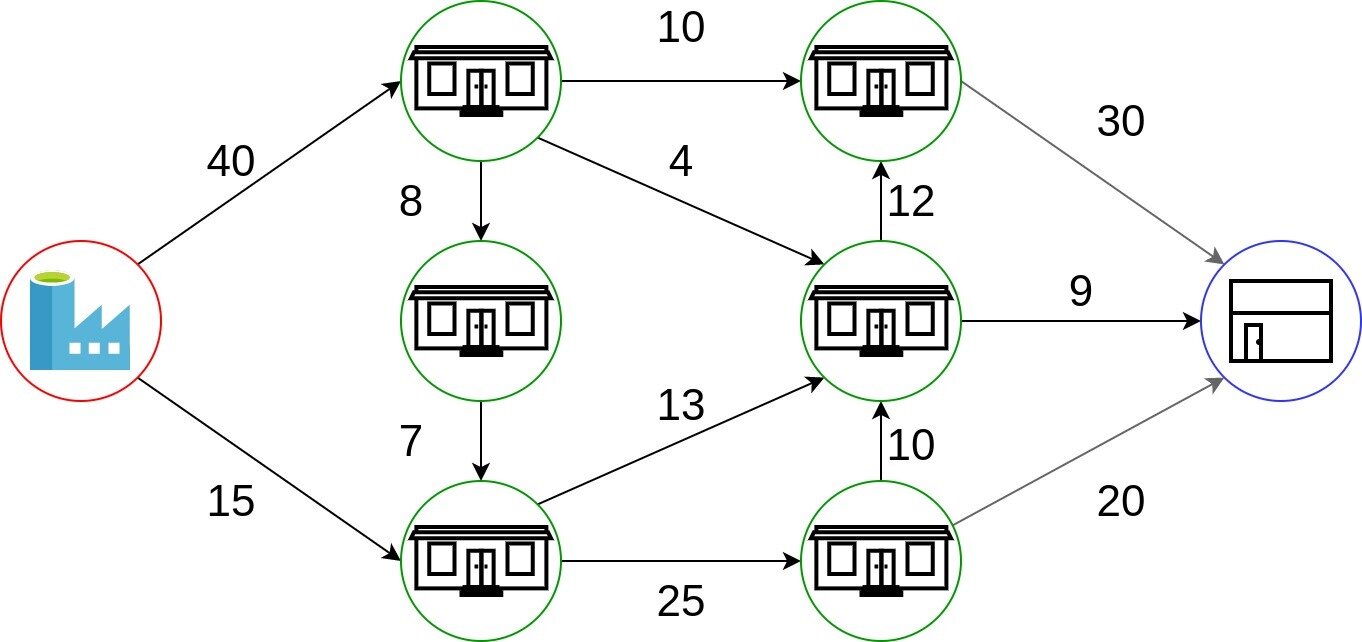
Los nodos de la 'red' reciben el mismo ritmo que el ritmo que despachan
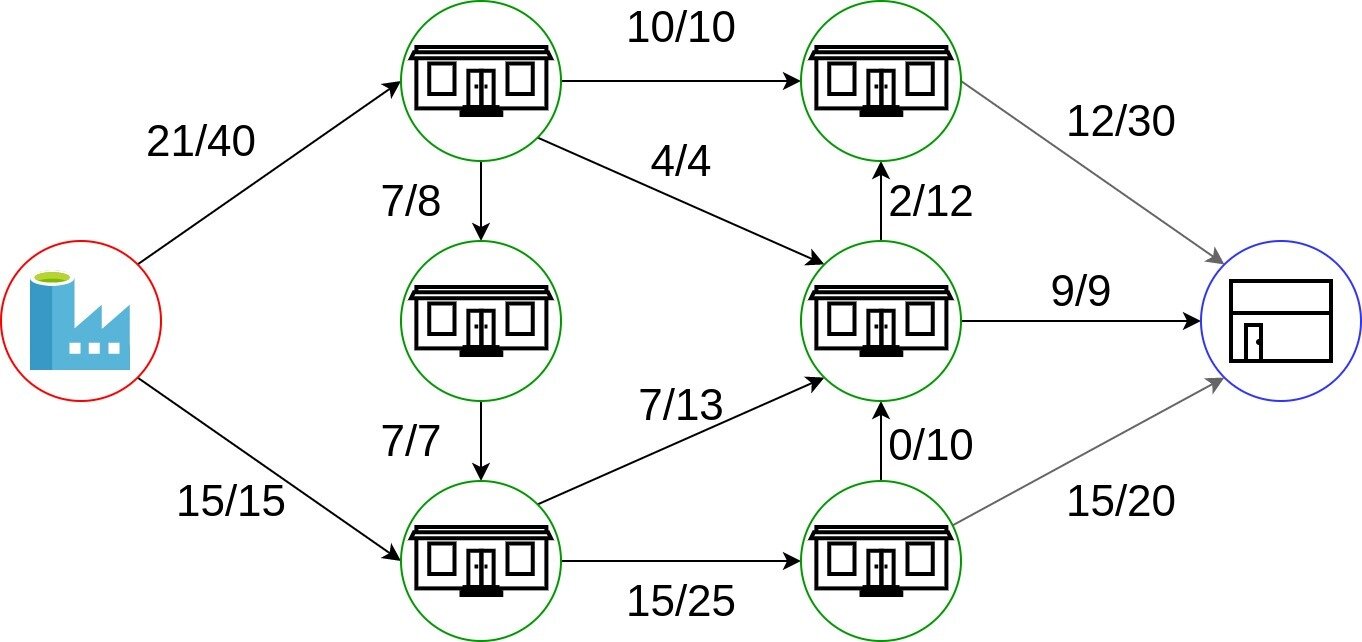
Los nodos de la 'red' reciben el mismo ritmo que el ritmo que despachan
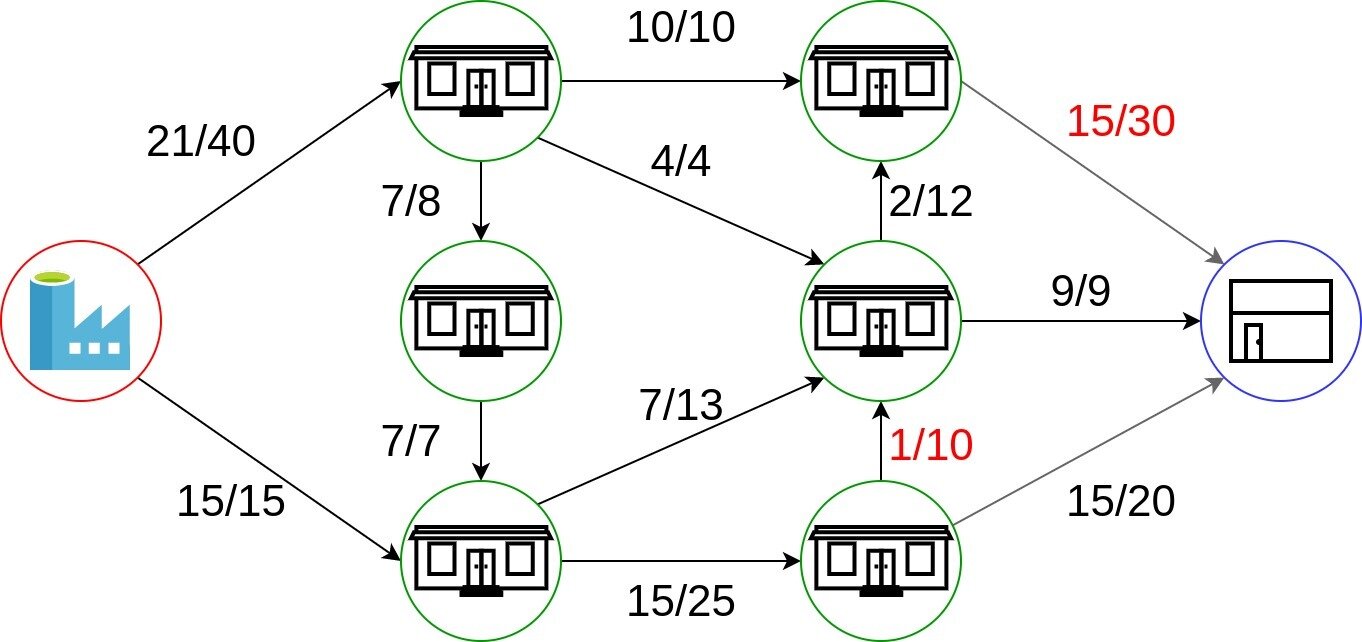
Cual es el mayor ritmo al que se puede despachar el material desde la 'fuente' al 'sink' dada una red particular?
Que es flujo?

El flujo de material en cualquier punto se define intuitivamente como el ritmo al cual el material se mueve
Formalización
Una red de flujo es un grafo dirigido G = (V,E) tal que cada vértice (u,v) tiene una capacidad c(u,v) > -1, además:
-
Si el vértice (u,v) pertenece a E no existe el vértice en la dirección contraria i.e. (v,u) -
Se distinguen dos vértices: 'fuente'(o), 'sink' (s)
-
Se asume que cada nodo pertenece a un camino entre f y s
Flujo
El flujo es una funcion con valores reales que satisface:
f : V \times V \rightarrow \mathbb{R}
(\forall_{u,w \in V} | 0 \leq f(u,w) \leq c(u,w))
(\forall_{u \in V - \{o,s\}} | \sum_{w \in V} f(u,w) = \sum_{w \in V} f(w,u))
valor del Flujo
El valor del flujo |f| de el flujo f se define como:
|f| = \sum_{w \in V} f(o,w) - \sum_{w \in V} f(w,o)
Normalmente no se consideran vértices hacia la 'fuente', luego:
|f| = \sum_{w \in V} f(o,w)
Ford-fulkerson
Este método iterativamente aumenta el valor del flujo. Empezando con f(u,w) = 0, para todos los nodos. En cada iteración, aumenta el valor de flujo en G encontrando un 'camino de aumento' en la 'red residual' asociada Gf

Red residual
Un nodo de la red de flujo puede admitir una cantidad adicional de flujo igual a la capacidad del vértice menos el flujo en ese vértice
\small
c_f(u,w)= \left\{ \begin{array}{l}
c(u,w) - f(u,w) \ \ \ si \ \ \ (u,w) \in E \\
\\ f(w,u) \ \ \ si \ \ \ (w,u) \in E \\
\\ 0 \ \ e.o.c
\end{array}
\right.
Red residual
Dada una red de flujo G=(V,E) y un flujo f, la red residual de G inducida por f es Gf = (V,Ef), donde:
E_f = \{ (u,w) \in V \times V : c_f(u,w) > 0 \}
Red residual
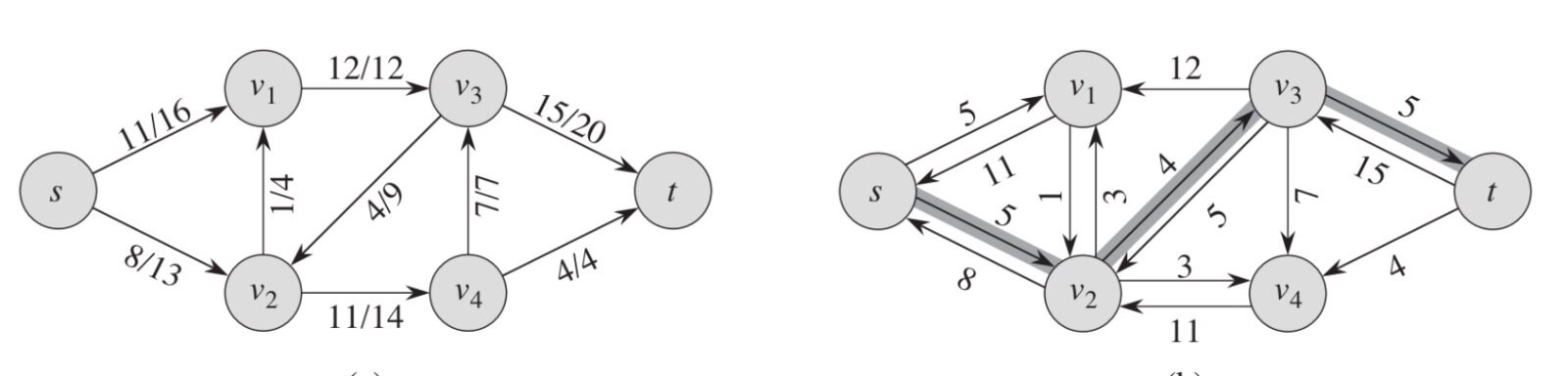
G
G_f
Camino de aumento
Dada una red de flujo G=(V,E) y un flujo f, un camino de aumento es un camino simple desde o hasta s

Ford-fulkerson
Este método iterativamente aumenta el valor del flujo. Empezando con f(u,w) = 0, para todos los nodos. En cada iteración, aumenta el valor de flujo en G encontrando un 'camino de aumento' en la 'red residual' asociada Gf

Cuando se para de iterar?

Cuando se para de iterar?
El flujo es máximo sii la red residual no contiene caminos de aumentoFord-fulkerson algoritmo
