Such- und Sortieralgorithmen
Sortieralgorithmen
Einfach
- BubbleSort
- SelectionSort
- InsertionSort
Komplex
- QuickSort
- HeapSort
- MergeSort
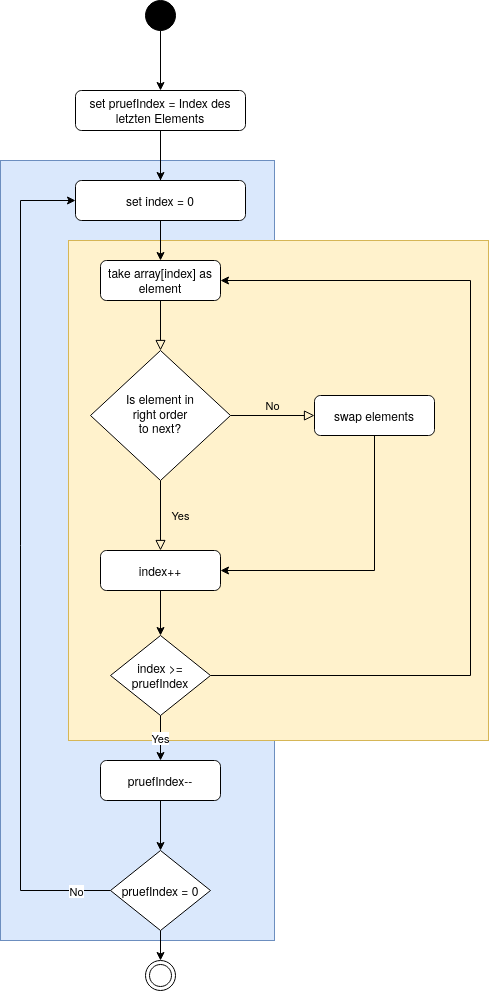
BubbleSort
Der BubbleSort sorgt im gelben Loop dafür, dass das größte Element ans Ende kommt.
Anschließend wird das Ende verkürzt und das zweitgrößte verschoben (s. blauer Loop)
| 3 | 6 | 2 | 1 | 10 | 13 | 11 | 15 | 1 | 4 | |||
| index = 9 | ||||||||||||
| i = 0 | 3 | 6 | 2 | 1 | 10 | 13 | 11 | 15 | 1 | 4 | ||
| i = 1 | 3 | 6 | 2 | 1 | 10 | 13 | 11 | 15 | 1 | 4 | tauschen | |
| i = 2 | 3 | 2 | 6 | 1 | 10 | 13 | 11 | 15 | 1 | 4 | tauschen | |
| i = 3 | 3 | 2 | 1 | 6 | 10 | 13 | 11 | 15 | 1 | 4 | ||
| i = 4 | 3 | 2 | 1 | 6 | 10 | 13 | 11 | 15 | 1 | 4 | ||
| i = 5 | 3 | 2 | 1 | 6 | 10 | 13 | 11 | 15 | 1 | 4 | tauschen | |
| i = 6 | 3 | 2 | 1 | 6 | 10 | 11 | 13 | 15 | 1 | 4 | ||
| i = 7 | 3 | 2 | 1 | 6 | 10 | 11 | 13 | 15 | 1 | 4 | tauschen | |
| i = 8 | 3 | 2 | 1 | 6 | 10 | 11 | 13 | 1 | 15 | 4 | tauschen | |
| i = 9 | 3 | 2 | 1 | 6 | 10 | 11 | 13 | 1 | 4 | 15 | ||
| index = 8 | ||||||||||||
| 3 | 2 | 1 | 6 | 10 | 11 | 13 | 1 | 4 | 15 | |||
| i = 0 | 3 | 2 | 1 | 6 | 10 | 11 | 13 | 1 | 4 | 15 |
Beispiel - Array mit 10 unsortierten Elementen
Etymologie
Wie Luftblasen im Wasser
steigen hier die größten zuerst auf und so weiter...
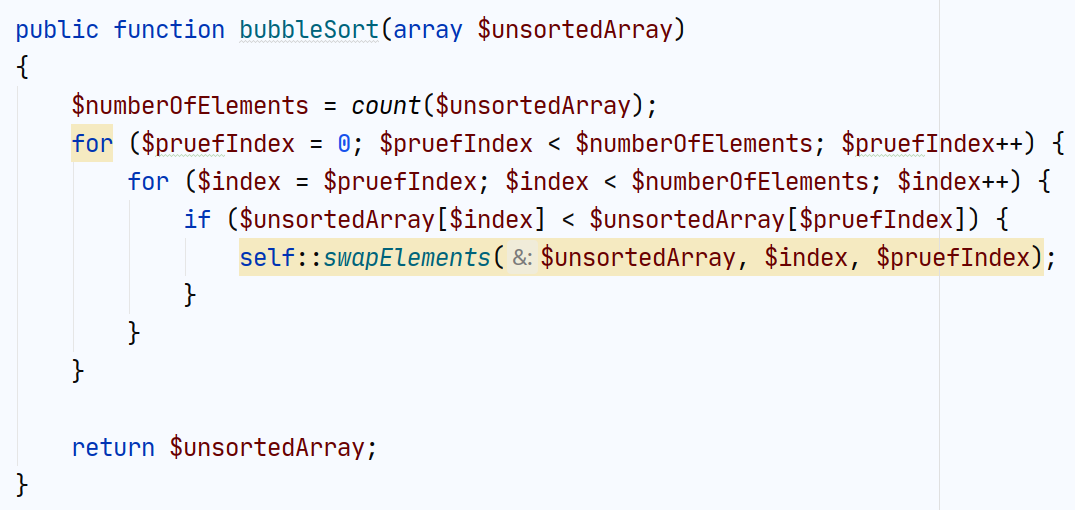
BubbleSort: PHP Code
SelectionSort
Der SelectionSort sucht im Array das minimale Element und schreibt es an den Anfang.
Dann behandelt er das restliche Array analog.
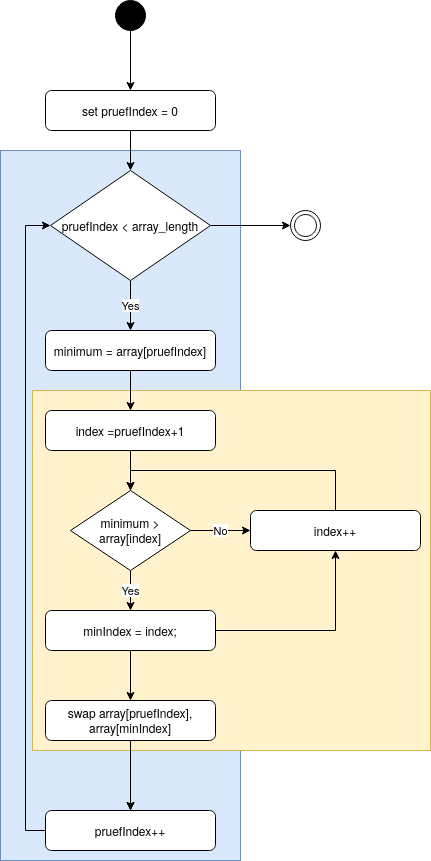
SelectionSort: PHP Code
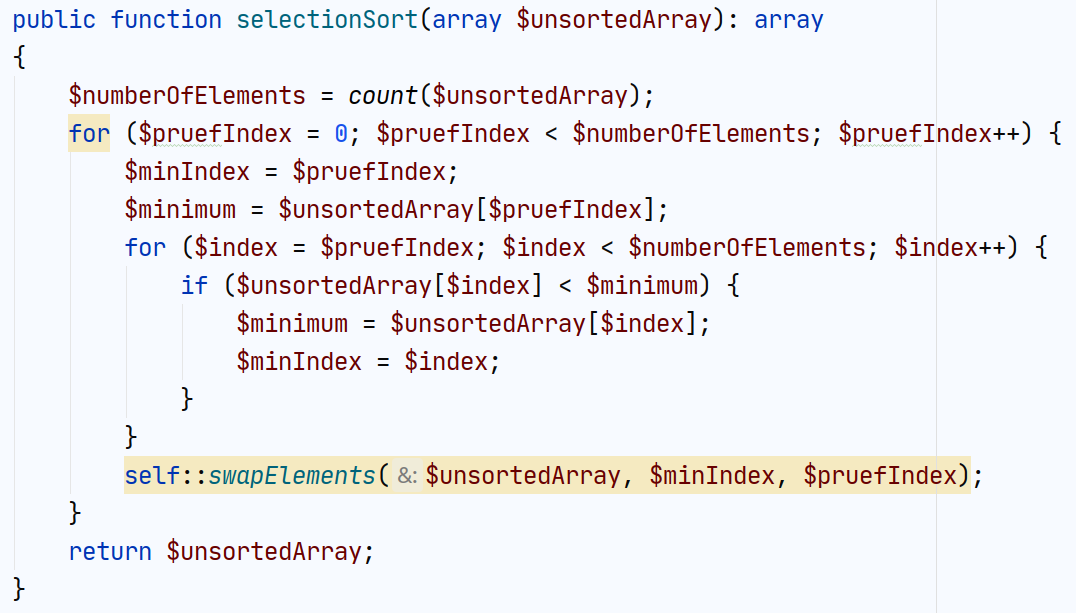
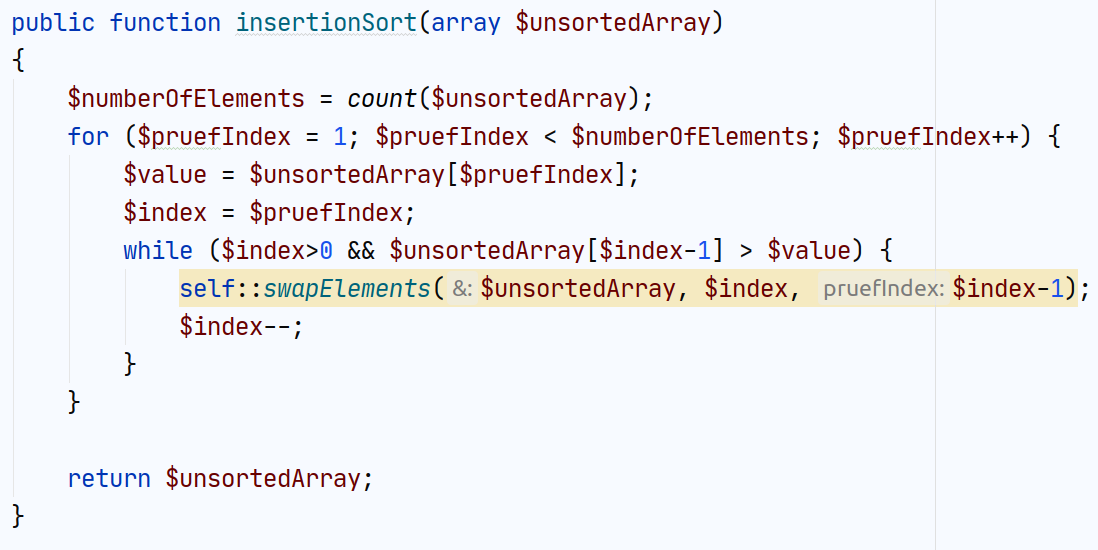
InsertionSort
Der InsertionSort arbeitet vergleichsweise wie beim Kartenspiel.
Man nimmt eine (weitere) Karte auf und sortiert sie zu den bereits aufgenommenen Karten richtig ein.

InsertionSort: PHP Code