Verschlüsselung

von

Michael Albrecht - Ausbilder FIAN
team neusta GmbH

Agenda

Motivation & Historie

Symmetrische Verfahren

Asymetrische Verfahren

Sonstiges

Vorstellungsrunde

Wie heiße ich und was ist meine Motivation FIAN zu werden?

Was bringe ich zum Thema Verschlüsselung bereits für Vorkenntnisse mit?

Was erwarte ich am Ende des Kurses?

Möglichst zu jeder Frage 1-2 Sätze und insgesamt nicht länger als 2 Minuten

Symmetrische Verfahren

"Schatz, hast Du den Schlüssel...?"

Symmetrische Verfahren - ROT 1

"ICH KOMME HEUTE UM VIER ZU DIR"

Zu verschlüsselnder Text

ROT 1:
A -> B
B -> C
C -> D
...

Auf diese Weise wird aus unserem Text:

"JDI LPNNF IFVUF VN WJFS AV EJS"

Symmetrische Verfahren - Cäsar

"ICH KOMME HEUTE UM VIER ZU DIR"

Zu verschlüsselnder Text

Cäsar: KRIEG

A -> K => ROT 10
A -> R => ROT 17
A -> I => ROT 8
A -> E => ROT 4
A -> G => ROT 6

Auf diese Weise wird aus unserem Text:

"STP...

Symmetrie

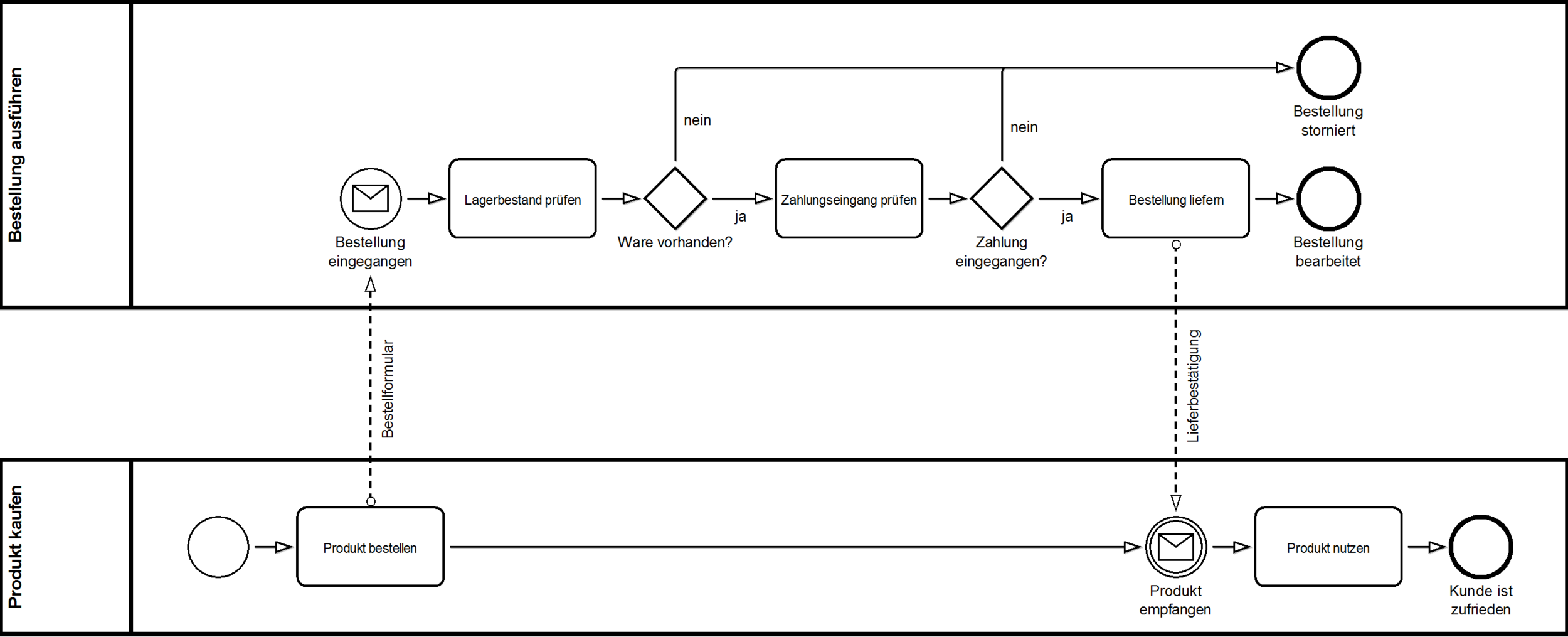
BPMN (Pool & Lanes)

Jeder aktive Part in einem Pool (hier: Gesamtszenario) genannt, erhält seine Swimlane, innerhalb derer die für den Prozeß relevanten Tasks ablaufen bzw. liegen.

Über Events oder direkte Aufrufe können Lane-übergreifend Tasks ausgelöst werden.

BPMN (Beispiel)

Asymmetrische Verfahren

"Ach, wie gut, dass niemand weiß..."

RSA - Verschlüsselung

Rivest - Shamir - Adleman

Nehmen wir zwei große Primzahlen:

p = 13; q = 23

N = p * q = 299

Wir wählen einen Exponenten e:

e = 7

(p - 1)*(q - 1) = 264 = 2³*3*11, also ggT(264, 7) = 1

Alice öffentlicher Schlüssel ist: (e,N) = (7, 299)

RSA - Verschlüsselung (Verschlüsseln)

Unsere zu verschlüsselnde Nachricht:

Message = 123

Bob verschlüsselt nun mit dem öffentlichen Schlüssel von Alice:

Coded = Message^e (mod N) = 123^7 mod 299
      = 425927596977747 mod 299
      = 150.

RSA - Verschlüsselung (private Key)

Alice privater Schlüssel d ist so, dass gilt:

e * d = 1 mod ((p-1)*(q-1))

Damit kann d wie folgt gewählt werden:

d = 151

denn: e * d mode (12*22) = (7 * 151) mod 264 = 1057 mode 264 = 1

RSA - Verschlüsselung (Entschlüsseln)

Zur Entschlüsselung rechnet man nun:

Message = Coded^d mod N

Damit kann d wie folgt gewählt werden:

Message = 150^151 mod 299 = 150^(1 + 6*25) mod 299
                          = (150 mod 299)* ((150^6 mod 299)^25)
                          = ... = (150 * 246) mod 299 = 123