Active Tactile Exploration

for Rigid Body State Estimation

Ethan K. Gordon, Bruke Baraki, Michael Posa

In Robotics, Models are difficult to build Online

  • Occlusions / Darkness

  • Clutter

  • Heterogeneous Materials

  • Broken Objects

State of the art: Tactile Model Learning

[1] Hu et al. "Active shape reconstruction using a novel visuotactile palm sensor", Biomimetic Intelligence and Robotics 2024

[2] Xu et al. "TANDEM3D: Active Tactile Exploration for 3D Object Recognition", ICRA 2023

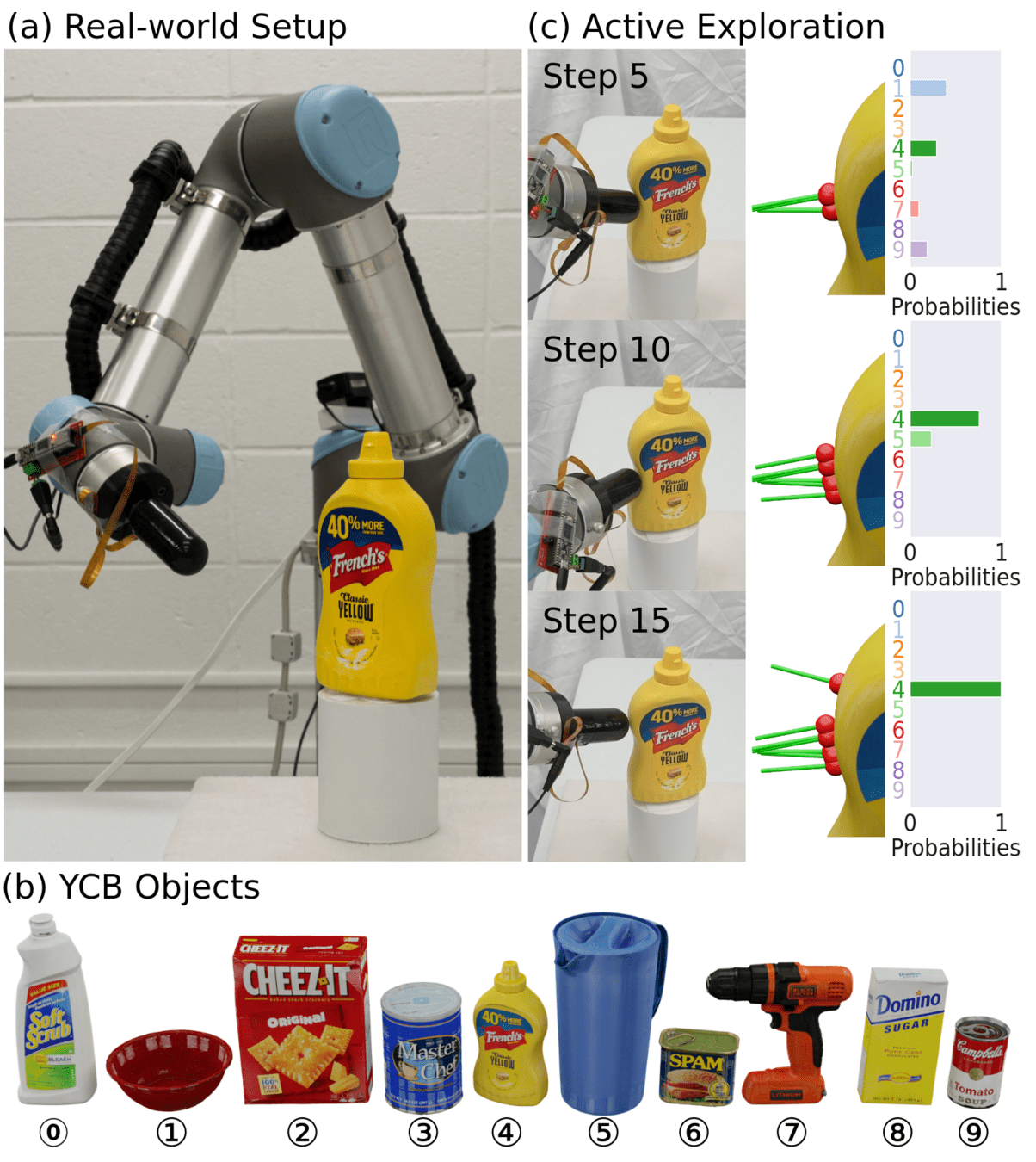
Static Objects: "assume a sensor that can detect contact before causing movement" [2]

Utilizes discrete object priors.

Shared Idea: Spatially Sparse Data -> Active Learning

Problem Formulation

Choose:

  • Robot Trajectory \(r[t]\)

Measure:

  • Contact Boolean \(c_t\)

  • Contact Normal \(\hat{n}_t\)

  • Proprioception

Find:

  • Object Geometry \(\theta^*\)

  • Object Pose \(x^*_T\)

Active Tactile Exploration: Problem Statement

?

r[t]

What we Choose: \(u\)

  • Robot Trajectory \(r[t]\)

What we learn: \(\theta\)

  • Object State \(x[t]\)

  • Geometry, Inertia, Friction \(\theta\)

\lambda_m[t]
\hat{n}_m[t]
\Theta = (x[t], \theta)

What we MEASURE: \(m\)

  • Contact? \(c[t] \in \{0,1\}\)

  • Surface Normal \(\hat{n}_m[t]\)

  • Contact Force \(\lambda_m[t]\)

Information: How well do we know \(\Theta\)?

Learning:         \(\tilde{\Theta} = \arg\min_\Theta \mathcal{L}^\Theta(u, m)\)

Noise Floor

\(\Theta\)

\(\mathcal{L}\)

\(\tilde{\Theta}\)

\(\Theta\)

\(\mathcal{L}\)

\(\tilde{\Theta}\)

\(\frac{\partial\mathcal{L}}{\partial \tilde{\Theta}}= 0 \)

How sensitive is this to uncertainty?

Low Info

High Info

(Fisher) Information       \(\mathcal{I} := \nabla_\Theta^2 \mathcal{L}\)

Each Measurement Contributes to Information

\lambda_m[t]
\hat{n}_m[t]
c[t]
\frac{(\nabla_\Theta \phi)^2}{(1+e^\phi)^2}
\tilde{\theta}
(\nabla_\Theta \hat{n})^2
(\nabla_\Theta \lambda)^2
\phi

Measurement:

\(\mathcal{I}\propto\)

Emergent Behavior:

"Get Close"

"Probe Corners"

(and edges if you don't know orientation)

"Push and Slide"

\(+\)

\(+\)

\tilde{\theta}
\tilde{\theta}

Exploration with Expected Information Gain (EIG)

Learn; Compute

Observed Info \(\mathcal{I}\)

Sample + Simulate

Expected Fisher Info \(\mathcal{F}\)

\(\max EIG := \log\det\left(\mathcal{F}\mathcal{I}^{-1} + \mathbf{I}\right)\)

Choose actions where simulated, expected Fisher info is distinct from Observed info.

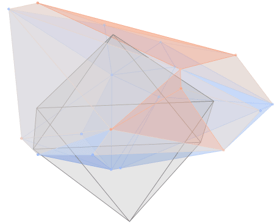
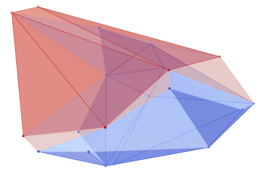
Learning with a Violation-Implicit Loss

Information Maximization In Action

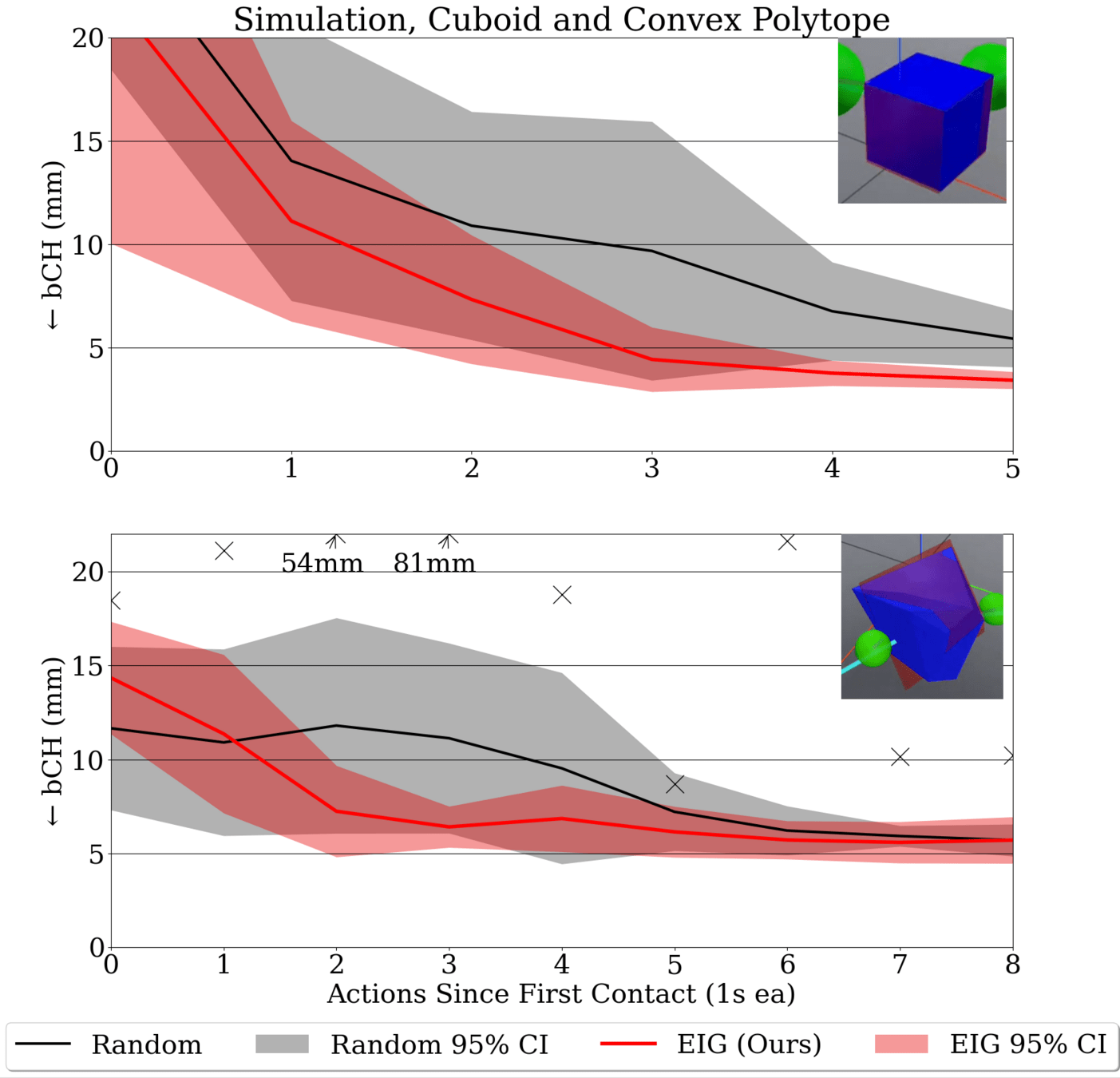
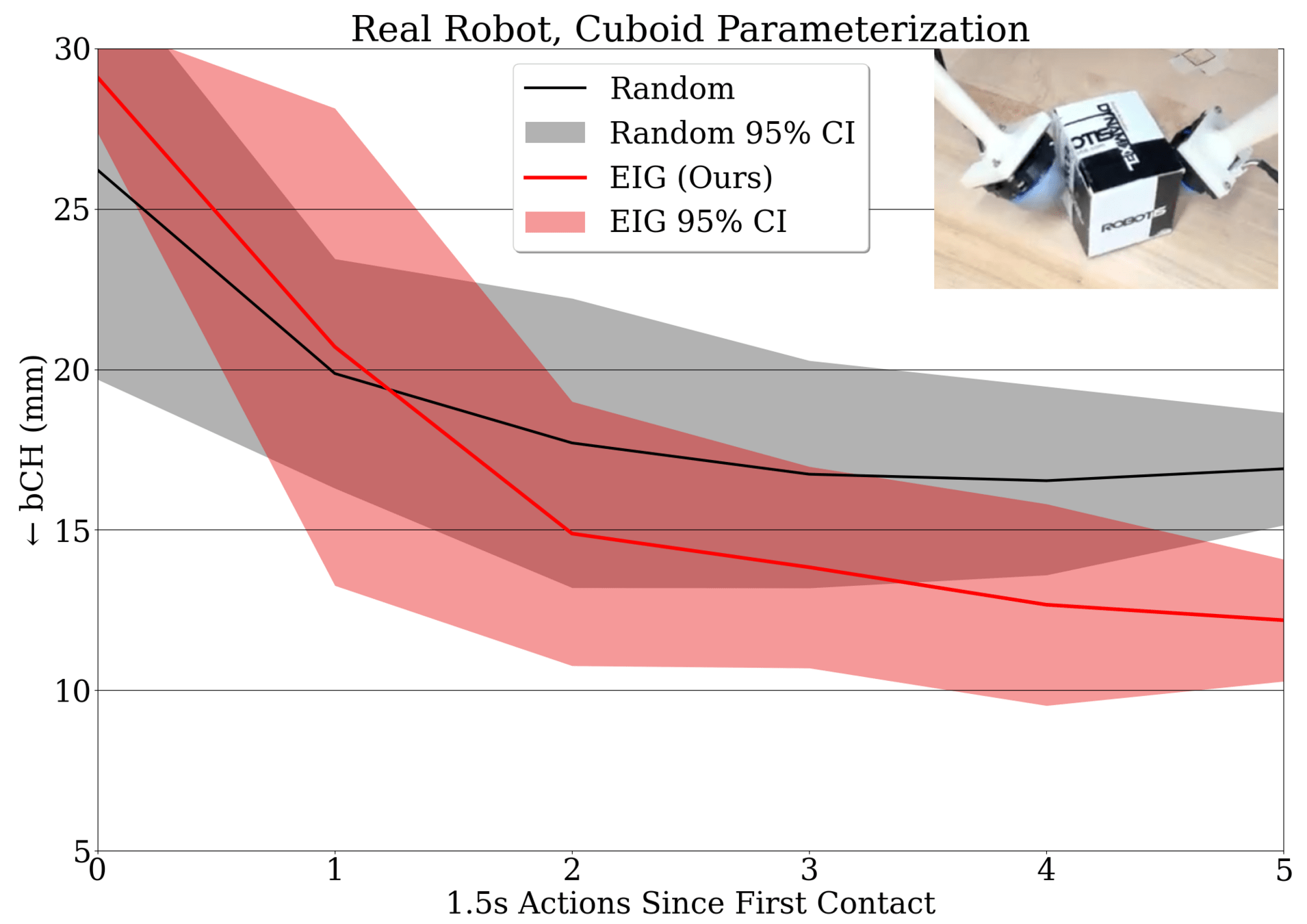
Preliminary Results

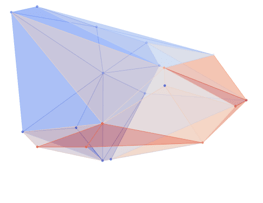
Green Sphere - Robot (simplified)

Red - Ground Truth

Blue - Our Guess

Preliminary Results

1. Force Action Z-Pinch

2. Learning....

3. Select New Action

X-Pinch Y-Pinch Z-Pinch

maximize Expected Info Gain

4. New Action: Y-Pinch

5. Learning...

X-Pinch Y-Pinch Z-Pinch

6. Select New Action

\sim 10^3
\sim 10^1
\sim 10^1
\sim 10^8
\sim 10^8
\sim 10^1

Green Sphere - Robot (simplified)

Red - Ground Truth

Blue - Our Guess

7. New Action: X-Pinch

Thank You!