Atomic Structure
M. Rocha
Physics 4C
The first hints of a quantized world
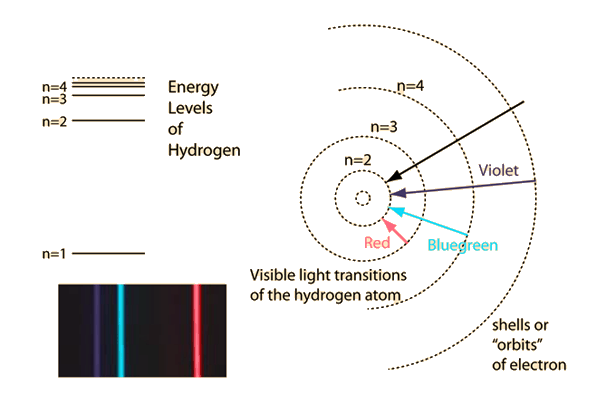
- The Bohr model of the atom (1913): In order to explain the emission and absorption lines of atoms, the orbits of electrons must be restricted to discrete energy levels
The energy of the emmited/absorved photons corresponds to the energy difference between energy levels
Quantum Particle In a Box



But the following must be true:



The most general possible solution is




Thus

Quantum Particle In a Box

Explanation of Quantized Energy Levels
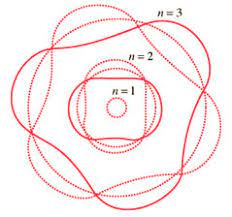
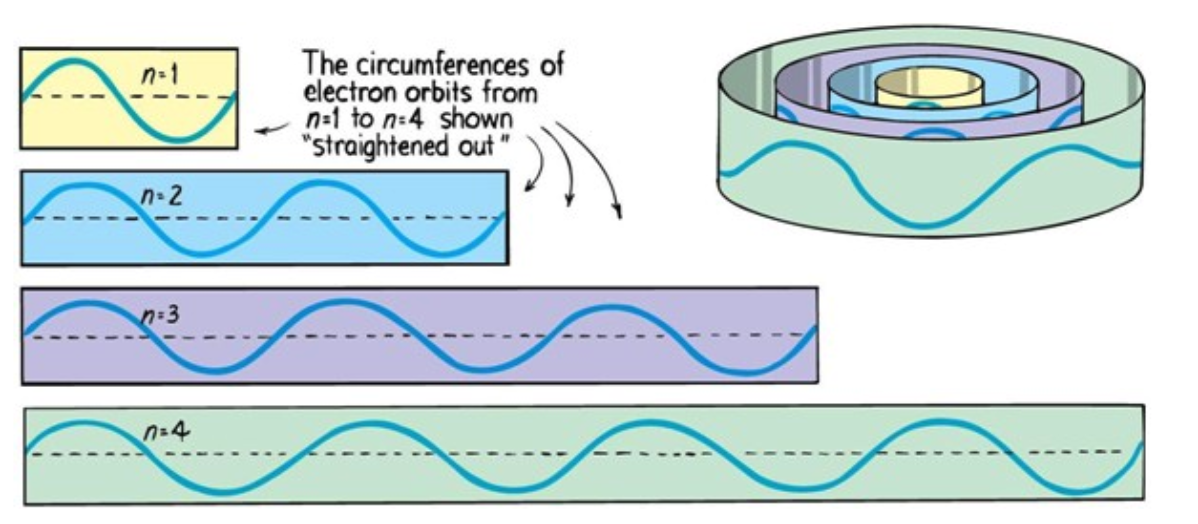
Electrons can only be at discrete energy levels (orbit radius), because the circumference of their orbit has to be an integer number of their wavelength in order to form standing waves, otherwise the experience destructive interference
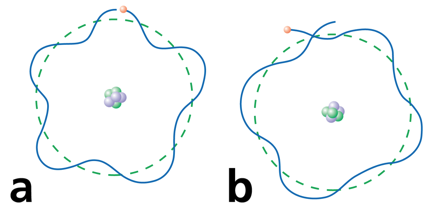
de Broglie's suggestion that electrons have a wavelength explained the quantized energy levels of atoms

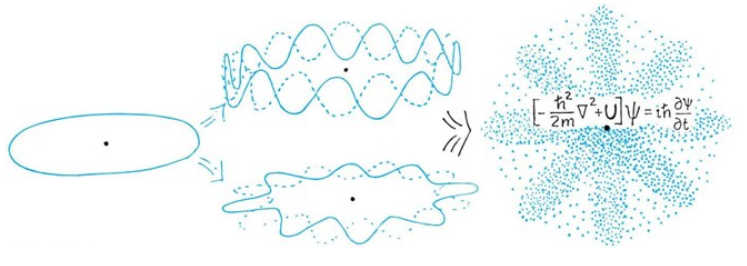
The Wave Function of Electron's in a Hydrogen Ataom

The Potential of an Hydrogen Atom

The Schrodinger's Wave Equation
For this we need an energy-momentum equation. For example the energy-momentum equation of a classical non-relativistic particle is given by

The Schrodinger's equation describes the dynamics of quantum system when they are subject to forces, i.e. when there are potential energies involved.
The Schrodinger's equation is the energy-momentum equation of a quantum system represented by a wave function
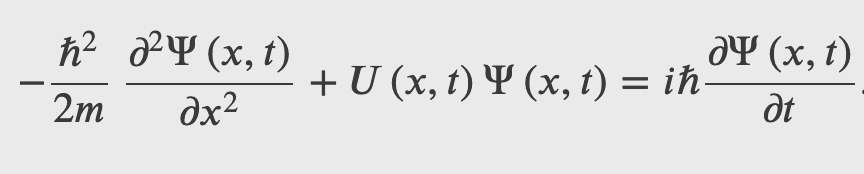
The Schrodinger's Wave Equation
Notice that for U(x,t) = 0, the Schrodinger's equation reduces to

A valid solution to this equation is the wave function of a free particle

Also if U does not depend on time, it is possible to show that

and since 𝐸=ℏ𝜔 the Schrodinger's can be written as

Spherical Harmonics
Spherical Harmonics represent possible standing waves / resonant modes in spherical symetry
The Schrodinger's Equation for a Hydrogen Atom

where 𝜓=𝜓(𝑥,𝑦,𝑧) is the three-dimensional wave function of the electron, 𝑚_𝑒 is the mass of the electron, and E is the total energy of the electron. Recall that the total wave function Ψ(𝑥,𝑦,𝑧,𝑡), is the product of the space-dependent wave function 𝜓=𝜓(𝑥,𝑦,𝑧) and the time-dependent wave function 𝜑=𝜑(𝑡).

Sphericall Symmetry
In addition to being time-independent, U(r) is also spherically symmetrical. To exploit this symmetry is better to work in spehrical coordinates




Spherical Symmetry
Due to the spherical symmetry of U(r), the solutions reduce to three equations: one for each of the three coordinates (𝑟,𝜃,and𝜙). Solutions to the time-independent wave function are written as a product of three functions:

The Schrodinger's equation can be written in spherical coordinates as follows







Valid solutions to Schrödinger’s equation 𝜓(𝑟,𝜃,𝜙) are labeled by the quantum numbers n, l, and m.





To determine the probability of finding an electron in a hydrogen atom in a particular region of space, it is necessary to integrate the probability density |𝜓_𝑛𝑙𝑚∣^2 over that region:
Probability Density

Each of the three quantum numbers of the hydrogen atom (n, l, m) is associated with a different physical quantity. The principal quantum number n is associated with the total energy of the electron, 𝐸𝑛. According to Schrödinger’s equation:


The Quantum Number n





The angular momentum orbital quantum number l is associated with the orbital angular momentum of the electron in a hydrogen atom. Quantum theory tells us that when the hydrogen atom is in the state 𝜓_𝑛𝑙𝑚
The magnitude of its orbital angular momentum is
The z-projection orbital angular momentum is
The magnitude of its orbital angular momentum is

The Quantum Numbers l and m

For example for l = 1
m = -1, 0, 1






Spectroscopic Notation
The Electron Spin
Spin is quantized in the same manner as orbital angular momentum. It has been found that the magnitude of the intrinsic spin angular momentum S of an electron is given by
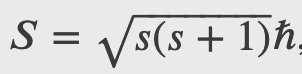






Pauli's Exclusion Principle
Pauli’s exclusion principle states that no two electrons in an atom have the same set of four quantum numbers.

Electron Configuration


The Periodic Table

Atomic Spectra



Fine Structure
X-Rays

Selection Rule:

Neglecting interactions between the electrons, the energy levels for an atom with atomic number Z is
The spectrum of sodium is analyzed with a spectrometer. Two closely spaced lines with wavelengths 589.00 nm and 589.59 nm are observed. What is the energy difference between these two excited states?
Checkpoint


If the doublet corresponds to the excited (valence) electron that transitions from some excited state down to the 3s state, what was the original electron angular momentum?


Selection Rule
Estimate the characteristic energy and frequency of the 𝐾_α X-ray for aluminum (𝑍=13)
Checkpoint
The energy difference between the L and K shells in a hydrogen atom is 10.2 eV. Assuming that other electrons in the L shell or in higher-energy shells do not shield the nuclear charge, the energy difference between the L and K shells in an atom with 𝑍=13 is approximately

