Gravity, Projectile Motion and Satellites

M. Rocha

Physics 1 - Week 4 - Chapters 9 and 10

The Universal Law of Gravity

Is the force pulling an apple down the tree the same as the one keeping the moon around the Earth?

The Universal Law of Gravity

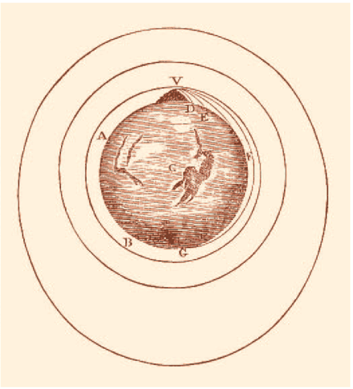
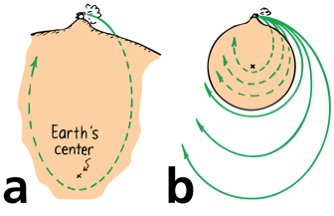
Newton's Mountain:

If you throw a stone horizontally fast enough, the stone keeps falling, but it never reaches the ground (because of the curvature of the Earth)

The Universal Law of Gravity

Is the force pulling an apple down the tree the same as the one keeping the moon around the Earth?

The Universal Law of Gravity

Is the force pulling an apple down the tree the same keeping the moon around the Earth?

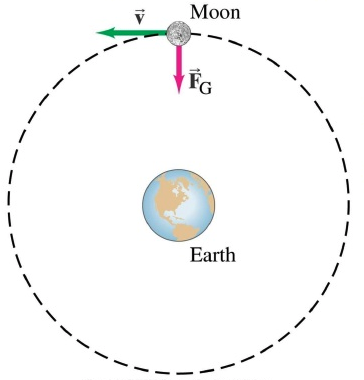
Yes it is!

Is the force of gravity

Force of Gravity

The force of gravity must be proportional to the product of the mass of the two objects interacting (i.e. M1*M2)

M2

\mathrm{F_G} \propto M_1 \cdot M_2

The Universal Law of Gravity

The force of gravity is inversely proportional to the square of the distance

\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}

This is because intensity spreads over the surface area of a sphere

The Universal Law of Gravity

\mathrm{F_G} \propto \frac{1}{\mathrm{distance^2}}

This is because intensity spreads over the surface area of a sphere

The force of gravity is inversely proportional to the square of the distance

The Universal Law of Gravity

\mathrm{F_G} \propto \frac{\mathrm{mass_1}\times\mathrm{mass_2}}{\mathrm{distance^2}}

\mathrm{F_G} = G \frac{m_1m_2}{d^2}

The force of gravity is proportional to the product of the mass of the objects and inversely proportional the square of the distance

G = 6.67 \times 10^{-11} \mathrm{\frac{N \ m^2}{kg^2}}

Checkpoint

An apple weighs 1 N at Earth's surface. How much does it weighs when it is 4 times as far?

4 R

\mathrm{F_G} = \frac{1}{\mathrm{4^2}}\mathrm{N} = \frac{1}{\mathrm{16}}\mathrm{N}

Weightlessness/Zero Gravity

Being weightless does not mean there is no gravity, what it means is that there is no support force (free falling)

Without a support force you experience weightlessness, but that doesn't mean there is zero gravity

Weightlessness/Zero Gravity

Without a support force you experience weightlessness, but that doesn't mean there is zero gravity

How zero gravity planes work?

Weightlessness/Zero Gravity

Ocean Tides

The ocean tides are caused by differences in the gravitational pull of the moon on opposite sides of Earth

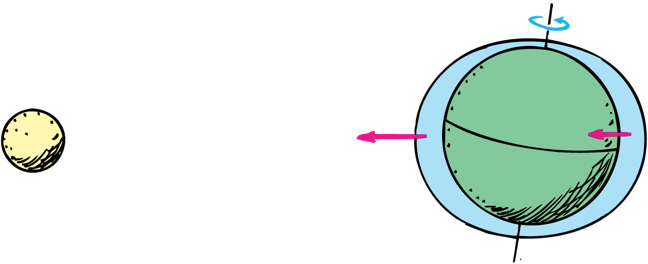
As the Earth rotates tides change during the day

Ocean Tides

The sun also contributes to ocean tides, but only about half as much as the moon

The difference in gravitational pull by the sun on opposite sides of Earth is very small

The Sun's pull on Earth is 180 times greater than the moon’s pull on Earth, so why aren’t tides due to the Sun 180 times greater than tides due to the Moon?

Ocean Tides

When the sun, the moon, and Earth are aligned, spring tides occur

Ocean Tides

When the attractions of the sun and the moon are at right angles to each other (at the time of a half moon), neap tides occur

Ocean Tides

Tides are most noticeable in fjords and basins due to a funneling effect. The Bay of Fundy has some of the most extreme tide swings in the planet (15+ m/48+ ft)

Projectile Motion and Satellites

Remember Free Fall Motion?

v = a \ t

d = \frac{a}{2} \ t^2

,

a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}

Checkpoint

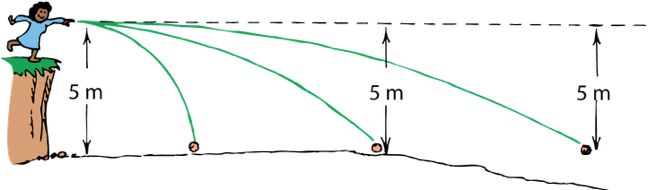
How far down (distance) would you fall in 1 second after you base jump from a cliff. Ignore air resistance.

d = 5 meters after 1 second

d = \frac{a}{2} \ t^2

a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}

,

Remember Free Fall Motion?

v = a \ t

d = \frac{a}{2} \ t^2

,

a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}

d = 5 meters after 1 second

5m in 1s

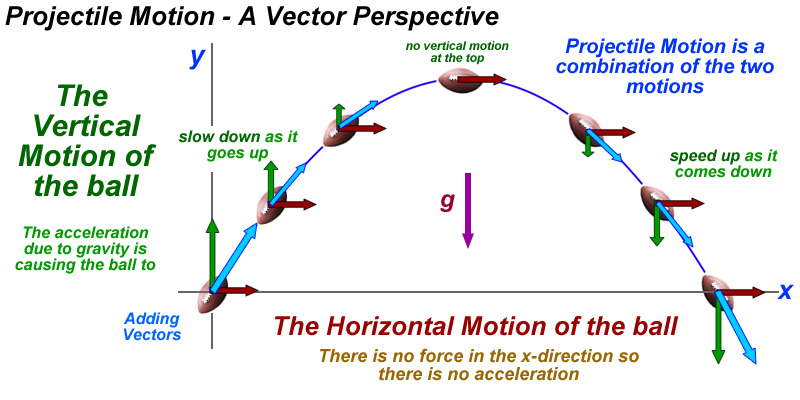
Projectile Motion is just Free Fall Motion with an horizontal velocity component

Free Fall:

V_y = at + v_{y_i}

V_x = 0

Projectile:

V_y = at + v_{y_i}

V_x = v_{x_i} (\mathrm{constant})

V_y

V_x

V_y

The key to understand Projectile Motion is to treat Vx and Vy separately

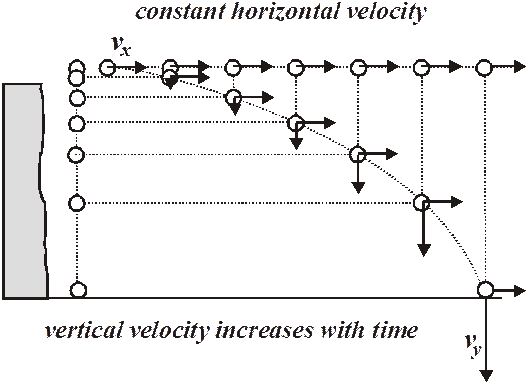
Vx and Vy are independent from each other

The key in understanding Projectile Motion is to treat Vx and Vy separately

Checkpoint

If I kick a soccer ball (from the ground), and it reaches a height of 20 meters, for how long would it be on the air before it hits the ground (HINT: The distance and time going up should be the same as when going down )?

d = \frac{a}{2} \ t^2

a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}

,

t_{up} = t_{down} = \sqrt{\frac{2d}{a}} = \sqrt{\frac{ 2 \ (20 \ m)}{10 \ m/s^2}} = \sqrt{4 \ s^2} = 2 \ s

Total time = tup + tdown = 4 seconds

Checkpoint

If I kick a soccer ball (from the ground) with a horizontal velocity of 20 m/s, and it reaches a hight of 20 meters, how far would it travel in the horizontal direction (i.e. how far would it land )?

d = \frac{a}{2} \ t^2

a = g = 9.8 \ \frac{m}{s^2} \simeq 10 \ \frac{m}{s^2}

,

t_{up} = t_{down} = \sqrt{\frac{2d}{a}} = \sqrt{\frac{ 2 \ (20 \ m)}{10 \ m/s^2}} = \sqrt{4 \ s^2} = 2 \ s

Total time = tup + tdown = 4 seconds

Horizontal Distance = 20 m/s ( 4 seconds) = 80 m

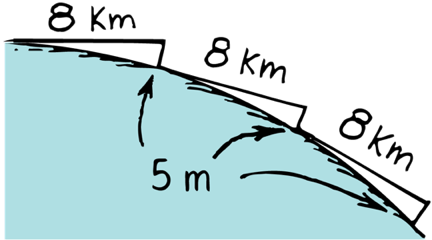
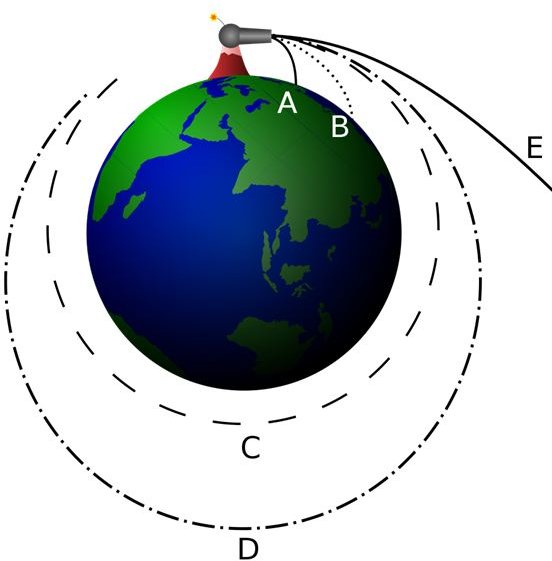
v_\mathrm{horizontal} = \frac{d_\mathrm{horizontal}}{t}

d_\mathrm{horizontal} = v_\mathrm{horizontal}\ t = 20 \frac{m}{s} \ (4 \ s) = 80 \ m

If a projectile falls 5m in 1s,

and the curvature of earth is so that it drops 5m for every 8 km

What happen if you throw a rock with an horizontal velocity of 8000 m/s = km/s (18,000 mi/h)?

Satellites

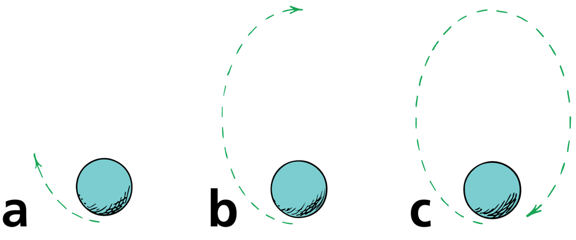
A satellite moves in an elliptical orbit

a) When the satellite exceeds 8 km/s, it overshoots a circle. b) At its maximum separation, it starts to come back toward Earth.

c) The cycle repeats itself.

Satellites

a) A projectile's path is a section of an elliptical orbit

b) a satellite moves in an elliptical orbit

Scape Velocity

Neglecting air resistance if you throw a rock with a velocity greater than 11.2 Km/s (25000 miles/h), it wont come back

Black Holes

At the surface of a black hole the force of gravity is so strong that not even light has enough velocity to scape

Black Hole Formation

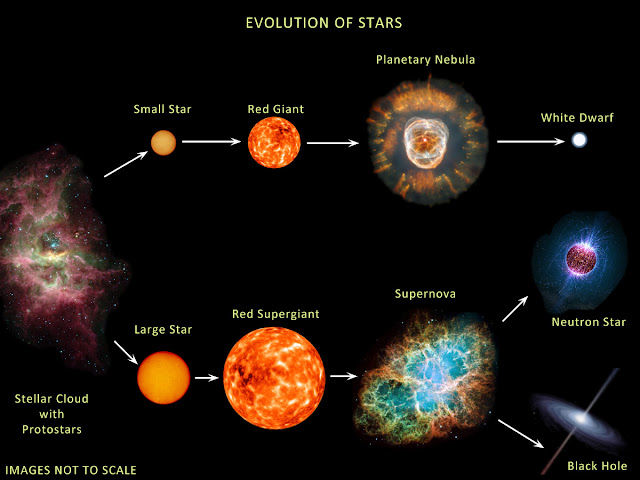
Only stars with a mass > ~1.5x the mass of the sun become black holes

Newtonian Gravity v.s. Einstein's

Einstein's

Gravity is the curvature of space and time due to massive objects

V.S.

Newtons

Gravity is a force field surrounding massive objects. Other masses interact with this force field

Gravitational Waves

First observed in 2015

The End

Energy Conservation on Satellites

On a circular orbit the force does not work and the PE and KE remain constant

On an elliptical orbit the force does some work and the PE and KE vary, however KE + PE is conserverd

Black Holes

The size of the sun is the result of a “tug of war” between two opposing processes: nuclear fusion (pressure) and gravitational contraction

If the fusion rate increases, the sun will get hotter and bigger. If the fusion rate decreases, the sun will get cooler and smaller

Black Holes

When the sun runs out of fusion fuel (hydrogen), gravitation will dominate and the sun will start to collapse

Neutron starts can pack up ~1.4x the mass of the sun on a radius that is the size of a city

In order to achieve such a high density they combine electrons and protons to form neutrons