Electromagnetic Waves,

Light and Color

M. Rocha

Physics 1 - Chapters 26 -27

Electromagnetic Waves

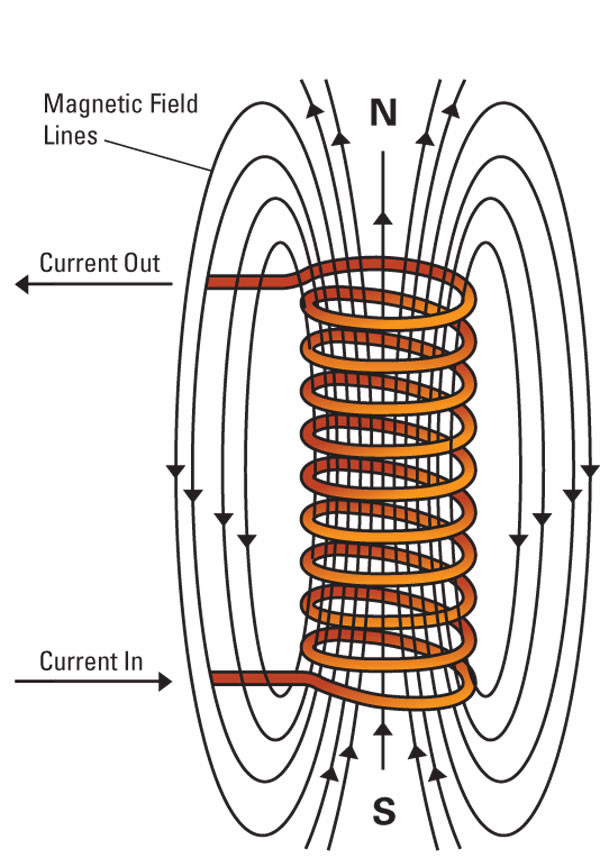
Moving charges produce magnetic fields

Moving magnetic fields produce electric fields

Current

and

Electromagnetic Waves

Oscillating charges create oscillating magnetic fields, which in turn create oscillating electric fields

The result are oscillating electric and magnetic fields that regenerate each other while traveling on space

Electromagnetic Waves

E&M waves need not material medium to travel!

They can travel on vacuum

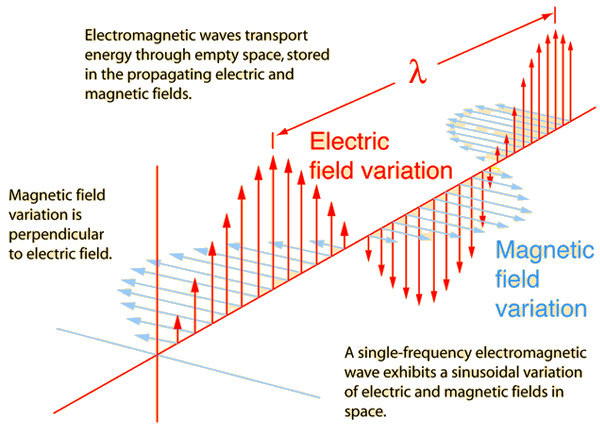
E&M waves have the standard properties of waves, but they all travel at the same speed, the speed of light

\mathrm{Wavelenght} \ (\lambda) \\ \mathrm{Frequency} \ (f) \\ \mathrm{Wave \ Velocity} \ (c) \\

c = 3\times10^8 \ m/s \\ (\mathrm{The \ speed \ of \ light})

c = f \cdot \lambda \\ f = \frac{c}{\lambda} \ , \ \ \lambda = \frac{c}{f}

The speed at which waves travel through a medium is related to the frequency and wavelength

Wave Speed

\mathrm{Wave \ Speed} = \frac{\mathrm{Wave \ Length}}{\mathrm{Period}} = \mathrm{Frequency} \times \mathrm{Wave \ Length}

Oscillations & Waves

The time required for a full oscillation (one round trip)

Period:

Frequency:

Number of oscillations per unit time

\mathrm{Frequency} = \frac{1}{\mathrm{Period}}

1 Hertz = 1 oscillation per second

For example, for a period of 2 seconds per oscillation, the frequency is ½ oscillations per second or ½ Hertz

Checkpoint

What is the wavelength of an E&M wave with a frequency

f = 3x10^4 Hz ?

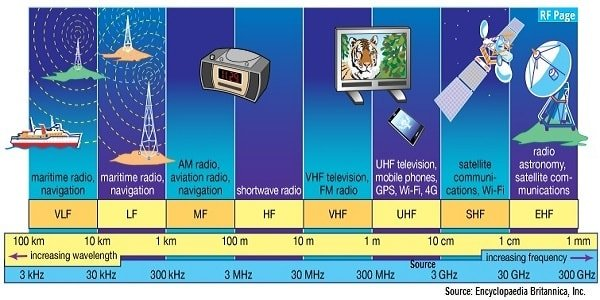
c = f \cdot \lambda \\ f = \frac{c}{\lambda} \ , \ \ \lambda = \frac{c}{f}

\lambda = \frac{c}{f} = \frac{3 \times 10^8 \ m/s}{3 \times 10^4 \ 1/s} = 10^4 \ m = 10 \ km

Electromagnetic Spectrum

Wavelength (m)

Light :

E&M waves in the visible range of the spectrum

Normal: Line perpendicular to interface

Checkpoint

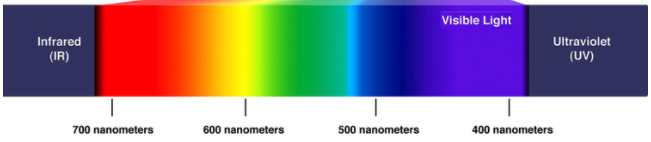
What color of light has the highest frequency?

Violet

Checkpoint

What color of light has the shortest wavelength?

Violet

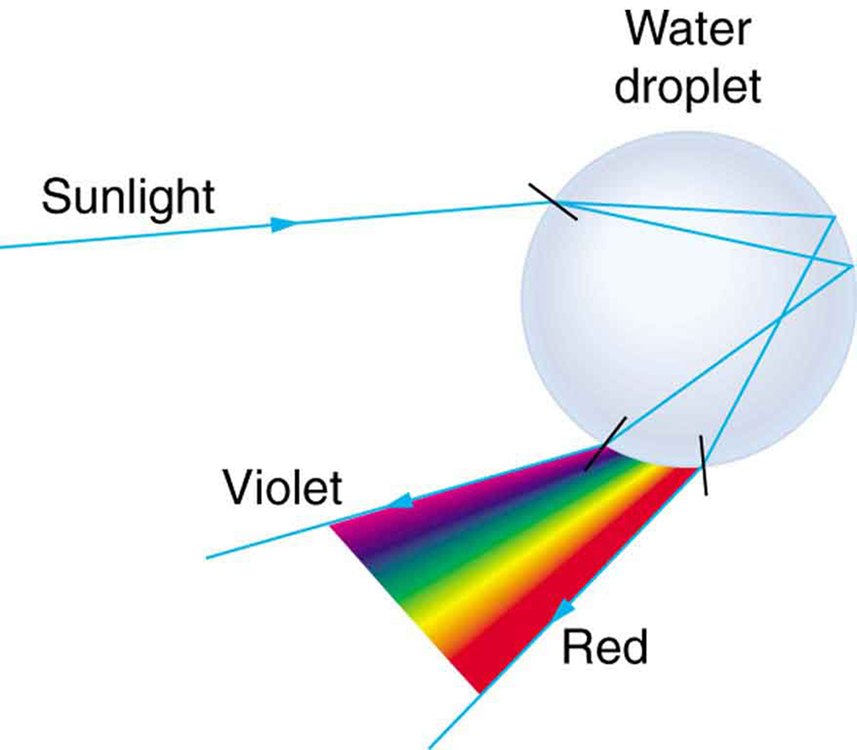
Refraction and Dispersion of Light

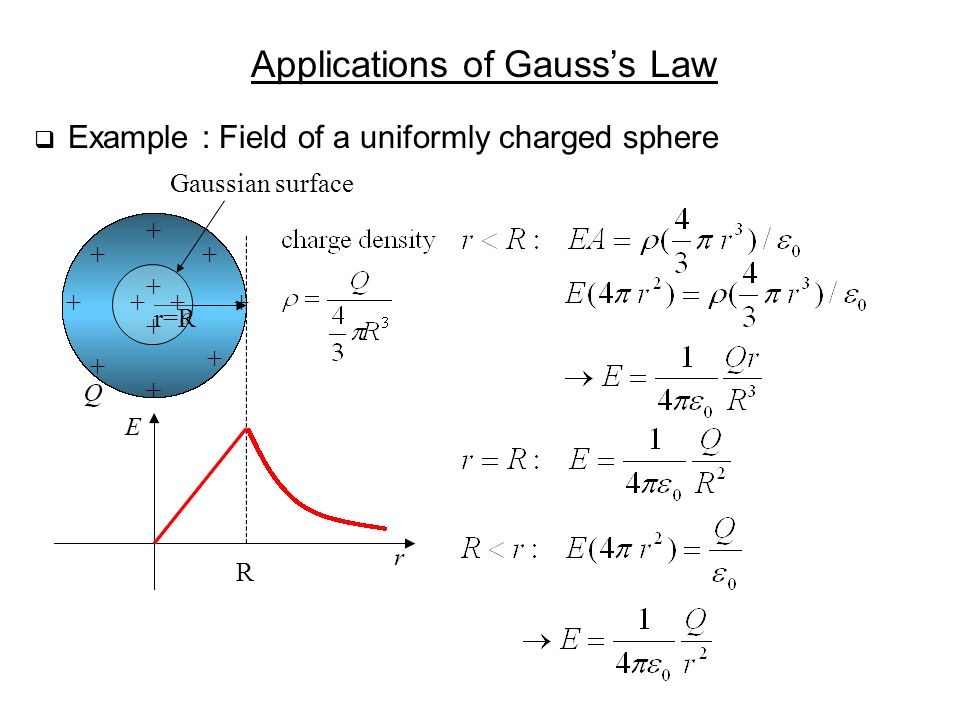
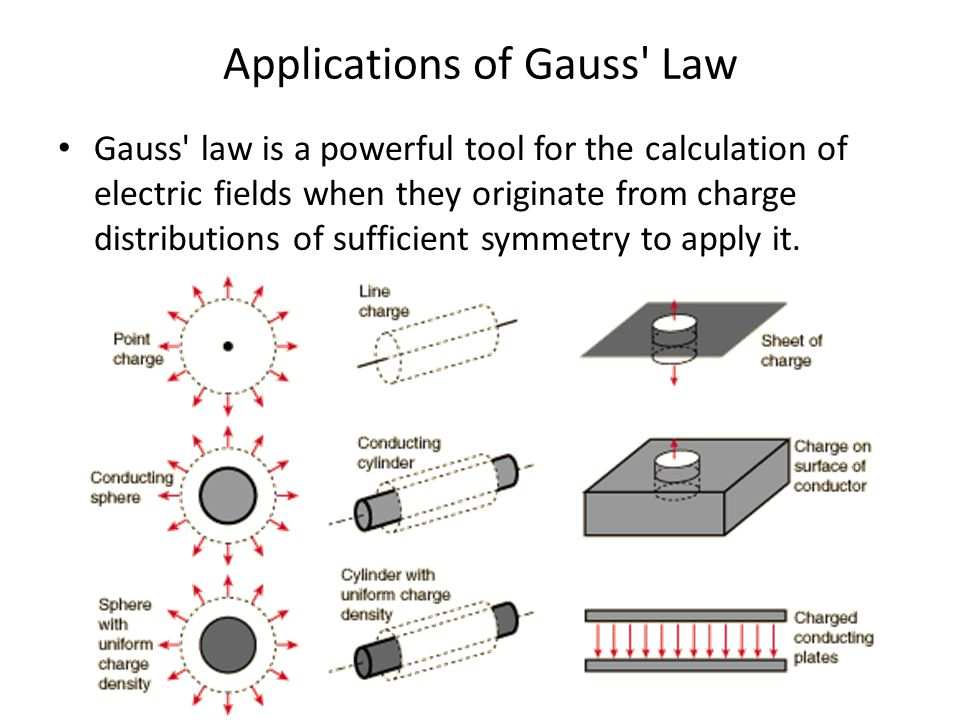
Gauss's Law

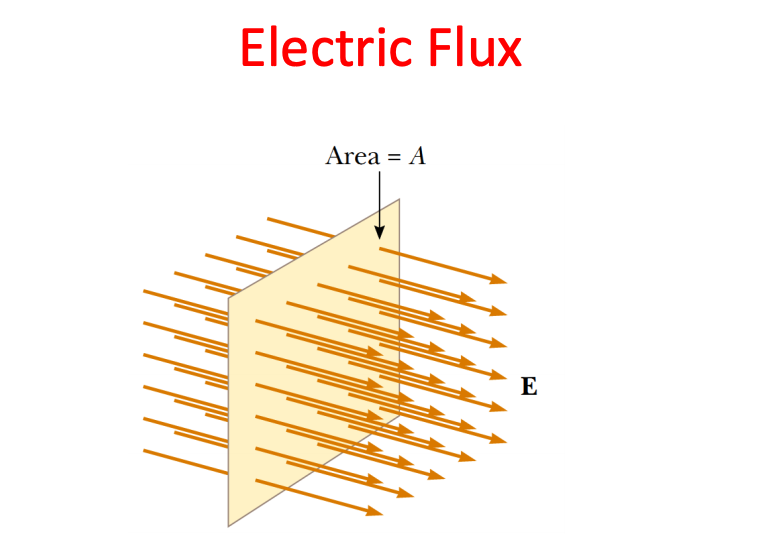
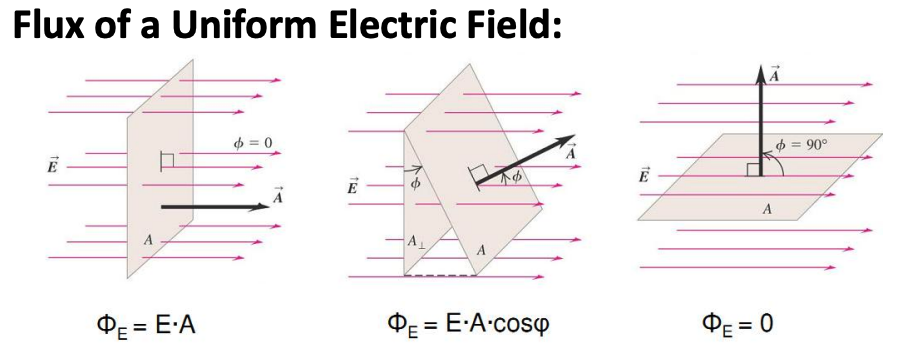
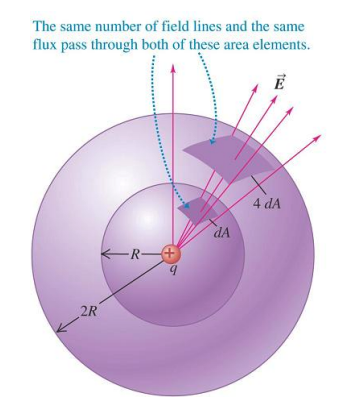
Gauss's Law for a point charge

E \propto 1/R^2 \\ A \propto R^2

Flux is independent of R

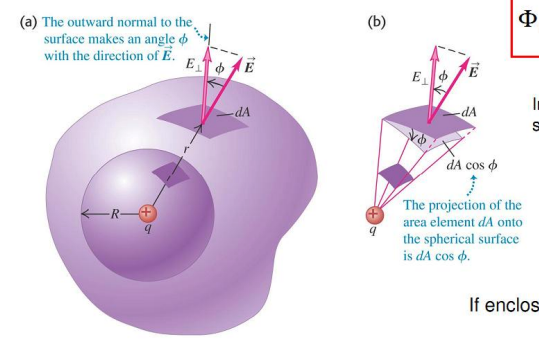
E_\perp \propto \cos{\phi} \\ A \propto 1/\cos{\phi}

Gauss's Law for a point charge

Flux is independent of the surface shape

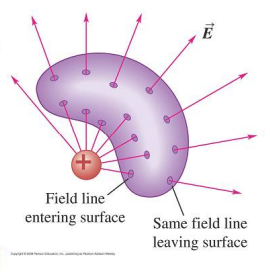
For charges outside of the enclosing surface flux cancels out

\Phi = 0

Exercises