Intro to Physics

M. Rocha  

Physics 11 - Week 1

What is Physics?

What is Physics?

Physics is the study of nature!

Physics (from Ancient Greek phusikē epistēmē). 

-> "knowledge of nature"

The main goal of physics is to understand how the universe behaves

For such an ambitious goal it is necessary look at the most fundamental components nature

Physics Is the natural science that involves the study of matter, and its motion and behavior through space and time, along with related concepts such as energy and force

Physics is the most fundamental science!

The Scale of Physics

From the smallest to the largest we know

The Scale of Physics

From Quarks

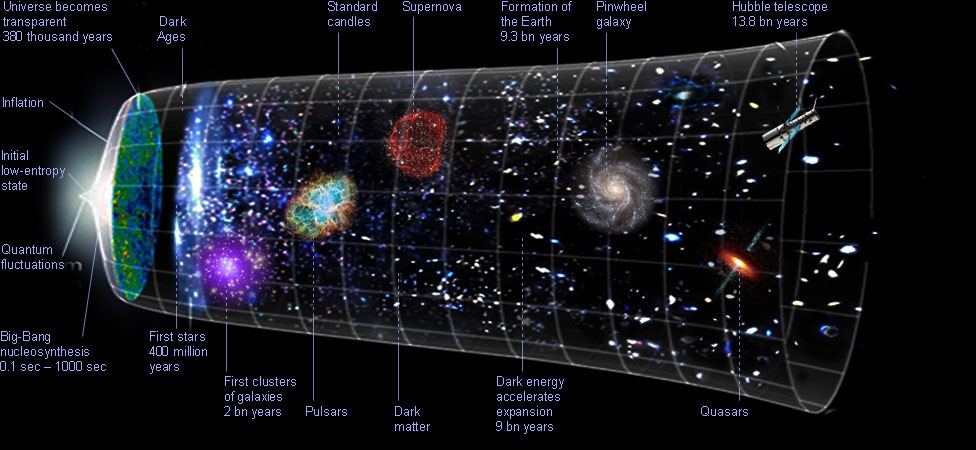
to

The Cosmic Horizon

< 10^{-18} meters
10^{26} meters
< 0.000000000000000001 \ m
100000000000000000000000000 \ m

Classical Physics (Before ~1900s): Is generally concerned with matter and energy on the non-extreme (human) scales

Modern Physics (After ~1900s): Is concerned with the behavior of matter and energy under extreme conditions or on a very large or very small scale

Classical vs. Modern Physics

Classical Physics: 

Modern Physics: 

Classical vs. Modern Physics

Mechanics

Themodynamics

Electro-Magnetism

Quantum Mechanics

Relativity

Covered in this course

Modern Physics

Classical vs. Modern Physics

Physics knowledge is validated through Science

So what is Science?

Science is asking nature what is TRUE, and accepting its answer no matter what your believes, perception or ideologies are

We ask nature what is TRUE through experimentation and observations

How we ask Nature what is True?

Experimentation and observations yield evidence!

Science is the practice of only accepting as a FACT what has been shown to be TRUE via experimental or observational evidence

What is Science?

  1. Recognize a question or a puzzle - such as unexplained fact.

  2. Make an educated guess - a hypothesis - that might resolve/explain the puzzle/fact.

  3. Predict consequences of the hypothesis.

  4. Perform experiments or calculations to test the predictions.

  5. Formulate the simplest general rule that organizes the three main ingredients: hypothesis, predicted effects, and experimental findings.

Scientific Method

A hypothesis becomes a theory or law only after many experiments have provided evidence for it not to be wrong

A hypothesis is only considered to be scientific if it can be proven wrong

Scientific hypothesis?

"Intelligent life exist on other planets somewhere in the universe"

"There is no other intelligent life in the universe"

No number of experiments can prove me right; a single experiment can prove me wrong" 

                                                                 -- Albert Einstein

Scientific hypothesis?

Can Science, Religion and Arts coexist in harmony?

Absolutely YES!

For as long as Religion and Art are open to accept/reject what nature has shown to be true/false

Science is not political, yet it can influence politics and culture

Science and Technology

Science 

Technology

Technology is applied science

Technology enables science

It is humans who use the technology, and humans who are responsible for how technology is used

Science Induces Deep Thinking and Expands Our Cosmology

But that doesn't mean it can't be fun!

Math Review

Math is the language of Physics

Math is the most abstract form of logic we have created.

Physics is understood through concepts, concepts are then represented in mathematical expressions.

E = mc^2

Mass is a representation of Energy. How much energy is associated to the mass of an objects is given by multiplying the amount of mass by the speed of light squared.

For example:

What is the result of the following operation?

Checkpoint 

\frac{10^6}{10^2} \frac{10^2}{1000} \frac{10^{7}}{10^{10}} = ?

Unit Analysis

mass = 100
[kg],
g = gram = \mathrm{weight \ of \ 1 \ cm^3 \ of \ water}

Physical quantity = Value x [Unit]

1 \ kg = 1000 \ g

Unit Analysis

[Energy \ \mathrm{unit}] = [Joule] = [kg \ (\frac{m}{s})^2]
[E \ \mathrm{unit}] = [mass \ \mathrm{unit}][speed \ \mathrm{unit}]^2
E = mass \times (\mathrm{something \ with \ speed \ units})^2
\Rightarrow E = mc^2
c = \mathrm{speed \ of \ light}

Units Work!

 Conversion of Units

1. Identify the equations that relate the units involved in the conversion.

2. Multiply by 1 in a way that the units you don't want cancel and the units you want remain.

3. Complete the operation by multiplying/dividing all the numbers involved in the conversion.

20 \ [kg] = \ ? \ [g]
1 \ [kg] \ = \ 1000 \ [g]
20 \ [kg] = \ 20 [kg]\times[\frac{1000 \ g}{kg}] = 20000 \ [g]
\Rightarrow \ 20 \ [kg] = 2\times10^4 \ [g]

 Conversion of Units

 Conversion of Units

75 \ [kWh] = \ ? \ [kg \ (\frac{m}{s})^2]
1 \ [kWh] = 3.6\times10^6 \ [J] \
75 \ [kWh] = \ 75 \ [kWh][\frac{3.6\times10^6 \ J}{ kWh}][\frac{kg(\frac{m}{s})^2}{J}]
75 \ [kWh] = 75 \times 3.6\times10^6 \ [kg(\frac{m}{s})^2]
1 \ [J] = 1 \ [kg(\frac{m}{s})^2]

,

=2.7\times10^{8} [kg(\frac{m}{s})^2]

Alpha Centauri is the closest star to us. Alpha Centauri is about  4x10^16 meters (m)  away from us. How far is Alpha Centauri in light years (ly) If 1 ly = 9.45x10^15 m?

Checkpoint 

4.2 ly

4\times10^{16} \ [m] = \ 4\times10^{16} \ [m][\frac{1 \ ly}{9.45\times10^15 \ m}] = 4.2 \ [ly]

For large distances astronomers prefer units of parsecs (pc) instead of light years (ly).

Andromeda (the closest spiral galaxy to us) is 2.4x10^22 m away. How far is Andromeda in Mega parsecs (Mpc) if 1 ly = 9.45x10^15 m and 1 pc = 3.26  ly ?

Checkpoint 

0.8 Mega pc, or 0.8 Mpc

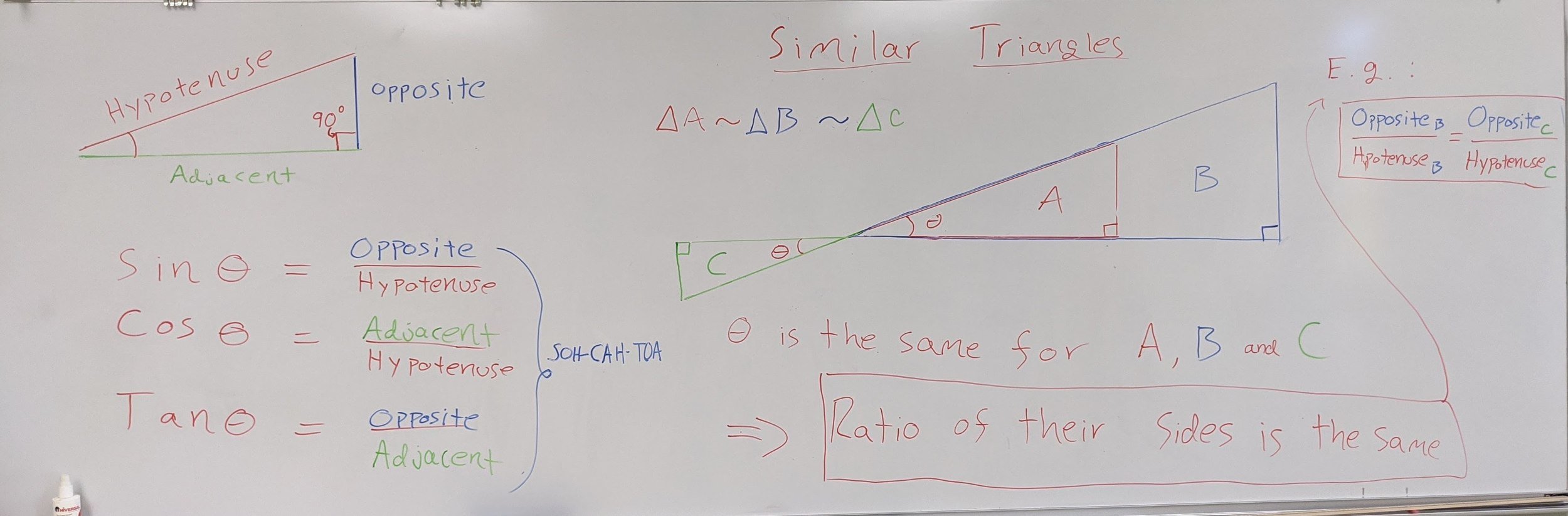
2.4\times10^{22} \ [m] = \ 2.4\times10^{22} \ [m][\frac{1 \ ly}{9.45\times10^{15} \ m}][\frac{1 \ pc}{3.2 \ ly}] = 0.08 \times 10^{7} \ [pc]
= 0.08 \times 10^{7} \ [pc] = 0.8 \times 10^{6} \ [pc]

Trigonometry Review

\theta =

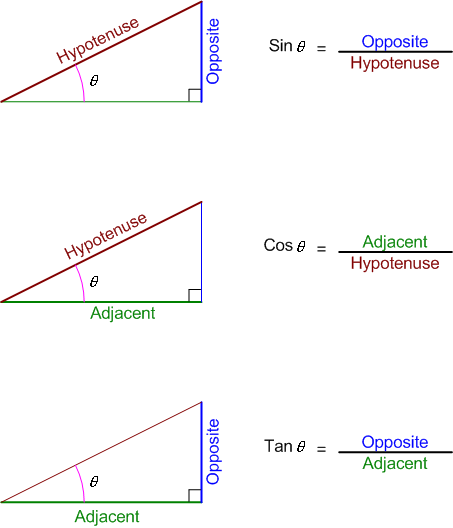
theta is the angle opposite to the right angle

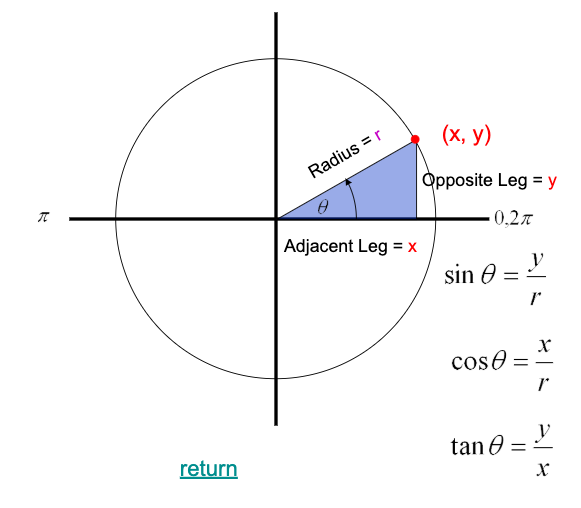
Circle Trigonometry 

\pi = 180^{\circ}
\pi/2 = 90 ^{\circ}
3\pi/2 = 270^{\circ}
2\pi = 360^{\circ}
\pi =\frac{\mathrm{Circunference}}{\mathrm{Diameter}} = \frac{\mathrm{Circunference}}{\mathrm{Radius} \times 2 }
\Rightarrow \mathrm{Circunference} = 2 \pi \times \mathrm{Radius}
L = \theta \times r

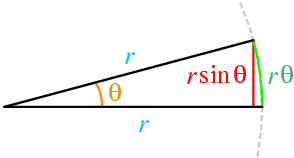
Small angle approximation

Arc Length = Angle in radians x Radius

r \sin \theta \approx r \ \theta
\approx

r = Hypotenuse

Adjacent

Arc Length and The Small Angle Approximation

r

Oposite = 

r \sin \theta

Oposite

L

\approx
\Rightarrow \sin \theta \approx \theta

Checkpoint 

What is the arc length L of a section of a circle with radius r = 4 meters, at an angle of                          

L = \theta \ r
\theta = \frac{\pi}{4}
L = \theta \ r = \frac{\pi}{4} \times 4 = \pi \ meters

Scientific Measurements

Measurements take us from qualitative to quantitative knowledge

Qualitative knowledge

Quantitative knowledge

The Sun is much larger than the Earth and the Earth is much larger than the Moon

The Sun is a lot farther from Earth than the Moon

We need measurements to know !

By how much?

Some Impressive Measurements by The Greeks

Size of Earth

Size of the Moon

Distance to the Moon

Distance to the Sun

Size of the Sun

First measured by Eratosthenes ~235 B.C.

Aristarchus ~ 240 B.C.

Formulated how to do this measurements  but was missing one key value, the Size of the Earth

Size of Earth

First measured by Eratosthenes ~235 B.C.

Size of Earth

First measured by Eratosthenes ~235 B.C.

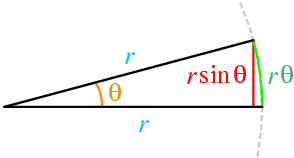
Size of Earth

First measured by Eratosthenes ~235 B.C.

d = \theta \ H
D = \theta \ R

,

\Rightarrow \theta = \frac{d}{H}=\frac{D}{R}
R =\frac{D \ H}{d}
R = 6370 \ km = 3959 \ miles

Size of the Moon

First measured by Aristarchus ~240 B.C.

During a total eclipse, it was observed that the moon traveled a distance equal to two and one half moon diameters while passing through the earth’s shadow.

Size of the Moon

First measured by Aristarchus ~240 B.C.

During a total eclipse, it was observed that the moon traveled a distance equal to two and one half moon diameters while passing through the earth’s shadow.

Size of the Moon

First measured by Aristarchus ~240 B.C.

Moon shadow tapers almost to a point in a solar eclipse

Size of the Moon

First measured by Aristarchus ~240 B.C.

The shadows cast by the moon and the earth are similar isosceles triangles

Size of the Moon

First measured by Aristarchus ~240 B.C.

This is a paralellogram, thus

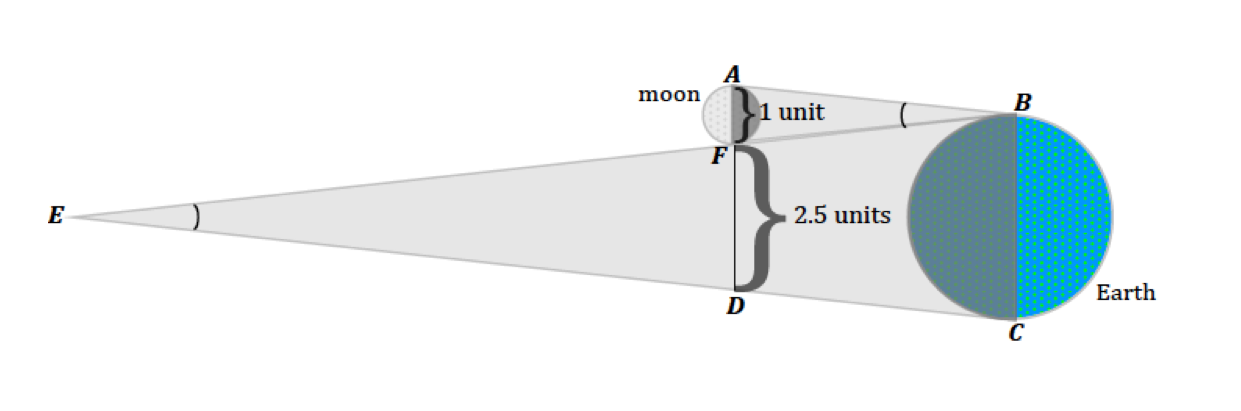
\overline{AD} = \overline{BC} = 3.5 \ \overline{AF} \Rightarrow \ D_{moon} = \frac{D_{earth}}{3.5}
D_{moon} = \frac{D_{earth}}{3.5} = 3474 \ km = 2159 \ miles

Distance to the Moon

First measured by Aristarchus ~240 B.C.

Distance_{moon} = Diameter_{moon}\frac{Distance_{coin}}{Diameter_{coin}} = 110 \ Diameter_{moon}
Diameter_{moon} = Distance_{moon} \ \theta
Diameter_{coin} = Distance_{coin} \ \theta

Distance to the Sun

First measured by Aristarchus ~240 B.C.

Distance_{sun} \ \sin{(180-x-90)} = Distance_{moon}
Distance_{sun} \approx 1.5 \times 10^8 \ km

Size of the Sun

Diameter_{sun} = \frac{d}{h} \ Distance_{sun}

Same as for the moon!

Because the sun is 400x farther than the moon but also 400x as big

Diameter_{sun} = Distance_{sun} \ \theta
d = h \ \theta \Rightarrow \theta = \frac{d}{h}

d = diameter of sun image

h = distance from pinhole to sun image

The apparent angular diameter of the sun is the same as that of the moon. 

Scientific Measurements

Measurements take us from qualitative to quantitative knowledge

Qualitative knowledge

Quantitative knowledge

The Sun is much larger than the Earth and the Earth is much larger than the Moon

The Sun is a lot farther from Earth than the Moon

The sun 400 times farther away than the moon

Sun is 109 times larger than earth, and 400 times larger than the moon

Accuracy, Precision, Errors and Uncertainty

  • Accuracy is how close a measurement is to the correct value for that measurement.
  • The precision of a measurement refers to how close the agreement is between repeated measurements (which are repeated under the same conditions)s).
  • Uncertainty is a quantitative measure of how much your measured values deviate from a standard or expected value. The uncertainty in a measurement, 𝐴, is often denoted as 𝛿𝐴, so the measurement result would be recorded as 𝐴±𝛿𝐴
  • Errors are the source of uncertainty. Systematic Errors/Bias are reproducible inaccuracies that are consistently in the same direction for every measurement. Random Errors are statistical in nature.

The End!