Maxwell Equations & EM Waves

Physics 4C

M. Rocha

Gasuss's Law

Gauss law for magnetism

Maxwell-Faraday equation (Faraday induction law)

 Ampere’s Law (with the addition of Maxwell)

You already know most of Maxwell's Equations!

You already know most of Maxwell's Equations!

Gauss's Law for Magnetism

Magnetic Poles

North Pole: Side where field lines point away from the source

South Pole: Side where field lines point into the source

Not known magnetic Monopoles

Unlike electric charges, cannot have just a North or just a South magnetic pole

Maxwell-Faraday Equation (Induction Law)

Induced Electric Fields

  • The induced emf due to changing magnetic fields is the result of the electric field doing work on the moving charges
  • The work done by 𝐄⃗  in moving a unit charge completely around a circuit is the induced emf ε
  • Faraday’s law can be written in terms of the induced electric field as

Maxwell-Ampere's Law

Maxwell's Addition To Ampere's Law

Ampere's Law

Maxwell suggested adding the displacement current 

I_d

Gasuss's Law

Gauss law for magnetism

Maxwell-Faraday equation (Faraday induction law)

 Ampere’s Law (with the addition of Maxwell)

Maxwell’s equations and the Lorentz force law together encompass all the laws of electricity and magnetism.

Lorentz force law

Electro-Magnetic Waves

\nabla \times \vec{\mathbf{E}} =-\frac{\partial \vec{\mathbf{B}}}{\partial t}
\nabla \times \vec{\mathbf{B}} = \frac{1}{c^2} \frac{\partial \vec{\mathbf{E}}}{\partial t}

In free space (no currents or charges), Maxwell's equations reduce to

\nabla \cdot \mathbf{B} =0
\nabla \cdot \mathbf{E} =0

,

,

=c

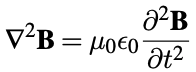
The speed of light

From maxwells equations in free space you can derive two symmetric wave equations (link to derivation)  

See an alternative derivation here 

Energy and Momentum of EM Waves

The time average of the energy flux is the intensity I of the electromagnetic wave and is the power per unit area.

where E0 and B0 are the maximum strengths/amplitude of the E and B fields and

The momentum can be found in terms of the Intensity of the EM wave, and is given by

The End