Thermodynamics

M. Rocha   

Physics 4C

1st Law of Thermodynamics

Connecting heat to mechanical energy

The Thermodynamic System

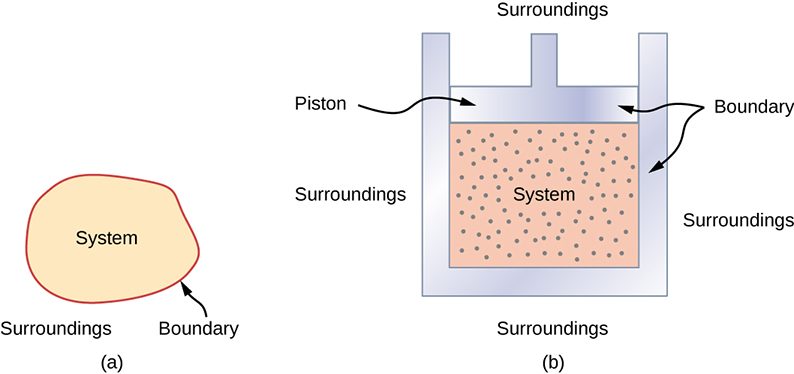
  • The system is contained by a boundary, acting as a wall that separates the system and the environment
  • Within the system, we assume thermal equilibrium
  • Most systems are known as an open system, which can exchange energy and/or matter with its surroundings.

Remember

Heat (Q) : Energy transfer due to temperature differences

Work (W): Energy transfer due to acting forces

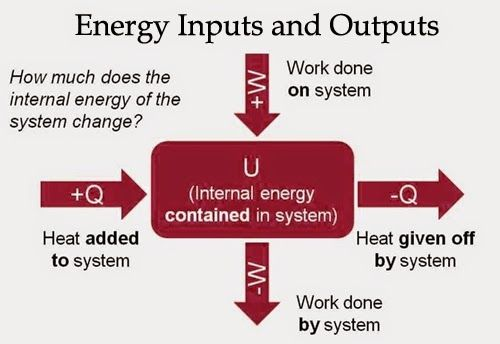
\Delta T = \frac{Q}{c \ m} \Rightarrow Q = \Delta T \ c \ m
W = F \ d

First Law of Thermodynamics

Whenever heat is added to a system, it transforms to an equal amount of some other form of energy

Energy is conserved!

First Law of Thermodynamics

Whenever heat is added to a system, it transforms to an equal amount of some other form of energy

Energy is conserved!

Adiabatic Process

Compressing or expanding a gas while no heat enters or leaves the system is said to be an adiabatic process

\Delta U = 0 - W \\ \Rightarrow \Delta U = -W
Q = 0

Adiabatic Process

When a gas adiabatically expands, it does work on its surroundings and gives up internal energy, and thus becomes cooler.

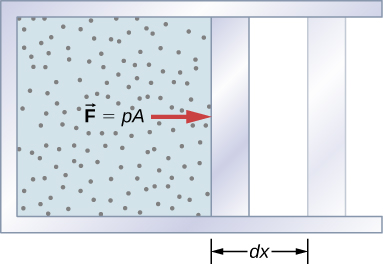
Work Done by a System

If the gas expands against the piston, it exerts a force through a distance and does work on the piston. If the piston compresses the gas as it is moved inward, work is also done—in this case, on the system. The work associated with such volume changes can be determined as follows:

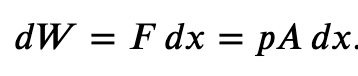
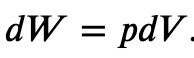
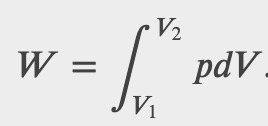
Where p is the gas pressure, V the volume of the system.

Work Done by a Perfect Gas

For a perfect gas, we have a well known equation of state relating pressure p and volume V

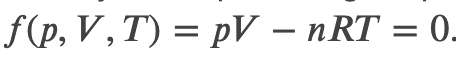
So we can define the work done by a perfect gas as

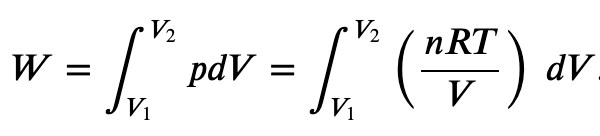
For a perfect gas, we have a well known equation of state relating pressure p and volume V

Notice the dependance of this integral on Volume (V) and Temperature (T). Because of this, the work done going from one point to another in the phase space is path dependent.

Work Done by a Perfect Gas

Isothermal process (constant Temperature):

If the gas is kept at a constant temperature T by keeping it in thermal equilibrium with a heat reservoir, then

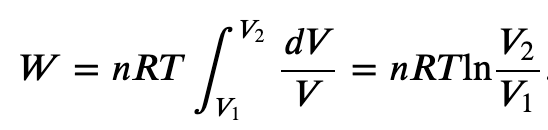
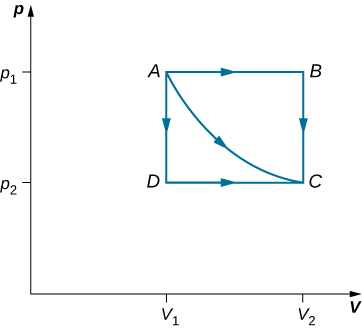
The path AC represents an isothermal process from points A to C

(p_1, V_1) \rightarrow (p_2, V_2)

Work Done by a Perfect Gas

Isobaric process (constant Pressure):

If the gas is kept at a constant pressure p, then

The path AB represents an isobaric process from points A to B

(p_1, V_1) \rightarrow (p_1, V_2)

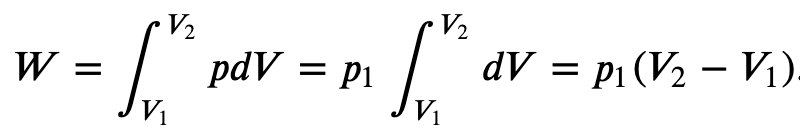
Work Done by a Perfect Gas

Isochoric process (constant Volume):

If the gas is kept at a constant volume V, then there is no work done as dV = 0

The path BC represents an isochoric process from points B to C

(p_1, V_2) \rightarrow (p_2, V_2)
W = 0

Work Done by a Perfect Gas

Thus, the work done for the transition A->C is path dependent

Work done by path AC:

(p_1, V_1) \rightarrow (p_2, V_2)

Work done by path ABC:

W = nRT \ln \frac{V_2}{V_1}
W = p_1(V_2-V_1)
W = p_2(V_2-V_1)

Work done by path ADC:

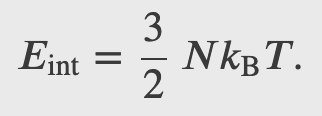
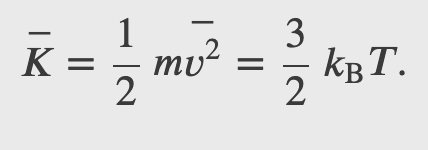
Internal Energy for an Ideal Monoatomic Gas

For a monoatomic ideal gas 𝑈𝑖 = 0, hence

The internal energy of a thermodynamic system is, by definition, the sum of the mechanical energies of all the molecules or entities in the system. If the kinetic and potential energies of molecule 𝐾𝑖 and 𝑈𝑖, respectively, then the internal energy of the system is the average of the total mechanical energy of all the entities:

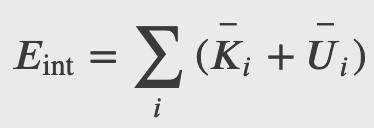
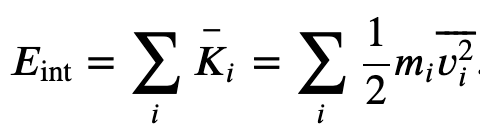
And using the result from the kinetic theory of gases

First Law of Thermodynamics for an Ideal Gas

The first law of thermodynamics tells us that by conservation of energy

Using the result of the internal energy for an ideal gas, then

dE_{int} = dQ - dW
dE_{int} = dQ - dW = \frac{3}{2}NkdT

Then the change in internal energy only depends in temperature (T), and since T = pV/Nk, the change in internal energy is path independent

The change in internal energy is path independent

First Law of Thermodynamics for an Ideal Gas

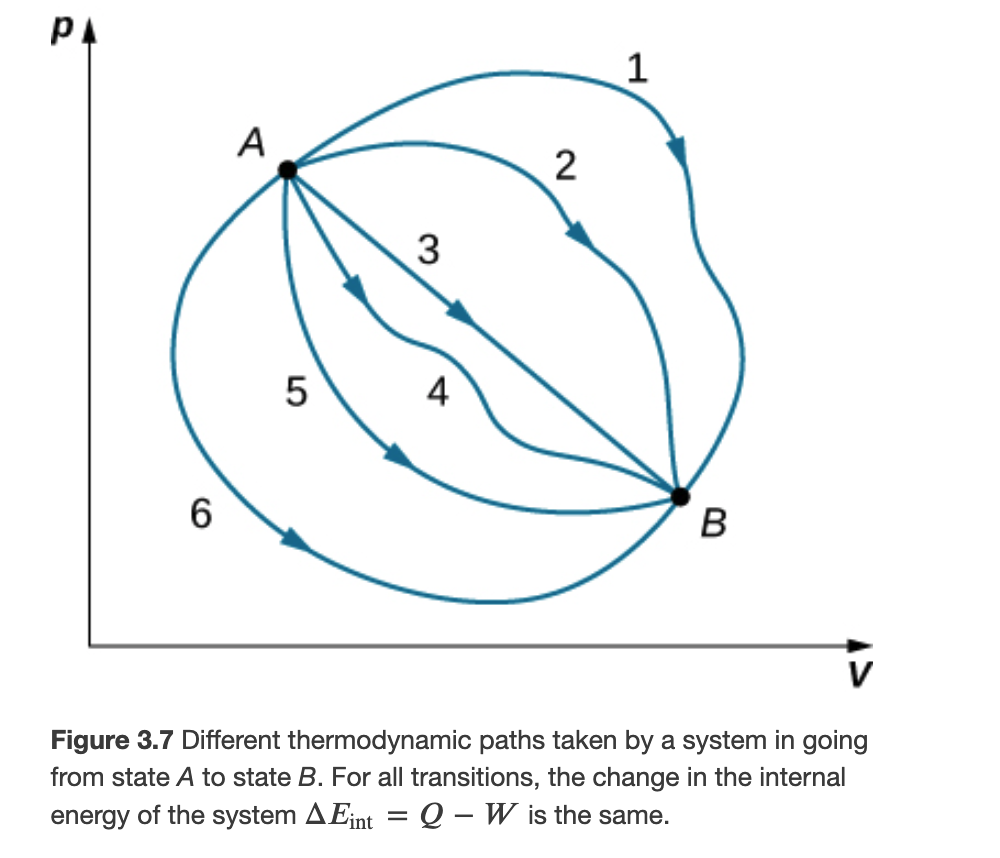
Although Q and W both depend on the thermodynamic path taken between two equilibrium states, their difference 𝑄−𝑊 does not.

Quasi-static vs Non-quasi-static Processes

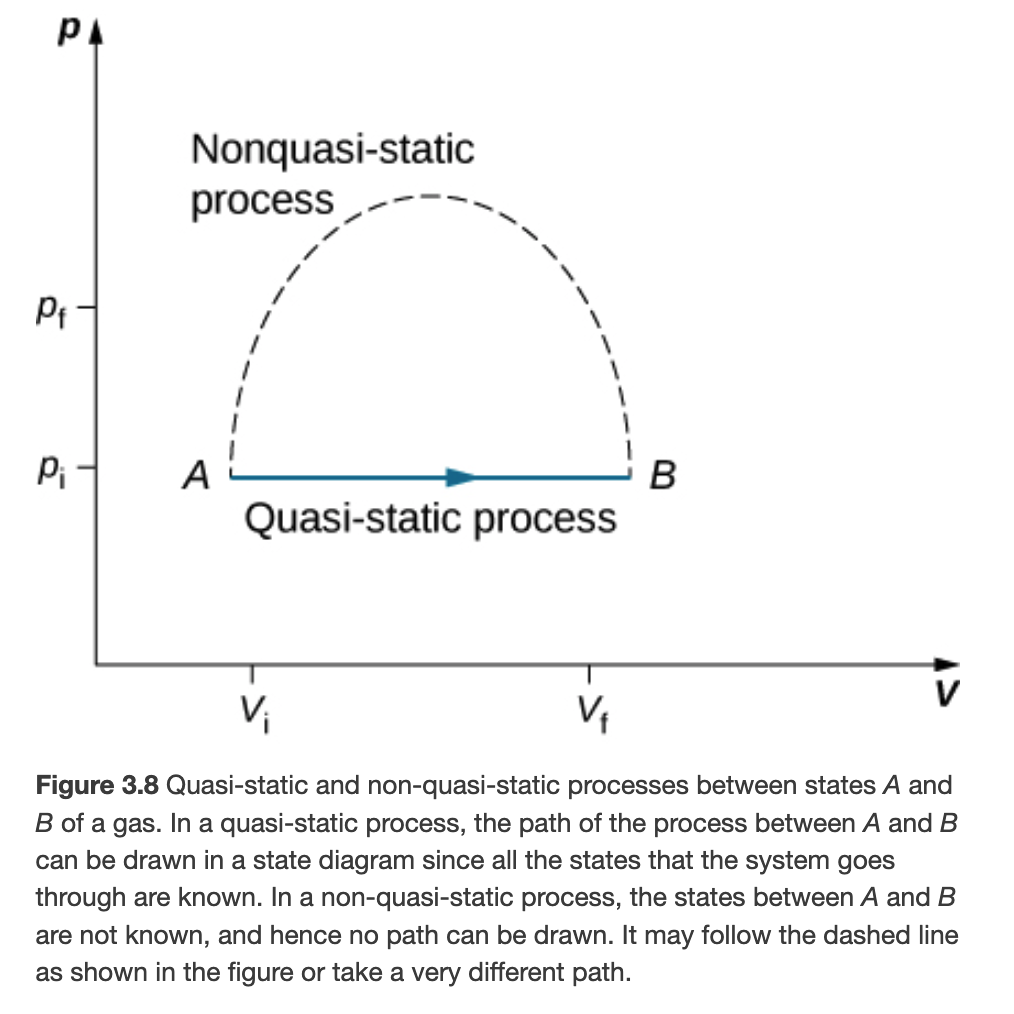
Heat Capacity at Constant Pressure

From the kinetic theory of gases, we found that the molar specific heat capacity of a gas at constant-volume is given by

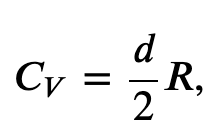
where d is the number of degrees of freedom of a molecule in the system.

Now, we can use the first law of thermodynamics to find a specific heat capacity at constant-pressure. We will do this for an ideal gas, but the result work as a good approximation non-monoatomic gases.

Heat Capacity at Constant Pressure

First we find the change in internal energy for a constant-volume process (W = 0):

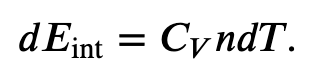
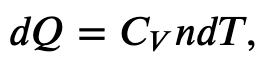
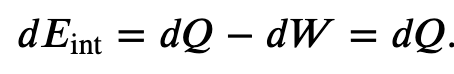
and 

Now we know the change in internal energy, which is path independent for an ideal gas since it only depends on temperature, so must be the same for an constant-pressure process

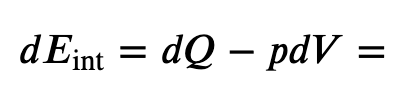
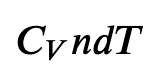
and for constant-pressure

then

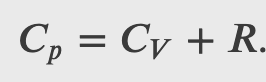
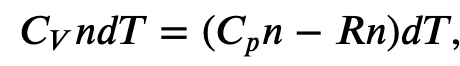
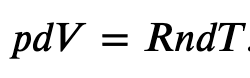
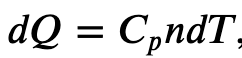
Since 

where 𝐶𝑝 is the molar heat capacity at constant pressure of the gas.

Cyclic Process

\Rightarrow Q = W
\Delta U = 0

We say that a system goes through a cyclic process if the state of the system at the end is same as the state at the beginning. Therefore, state properties such as temperature, pressure, volume, and internal energy of the system do not change over a complete cycle:

Adiabatic Process for an Ideal Gas

Using the internal energy change we found in terms of Cv, we can write the first law of thermodynamics for an ideal gas in an adiabatic process (dQ=0) as follows:

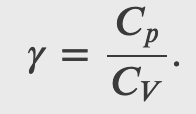
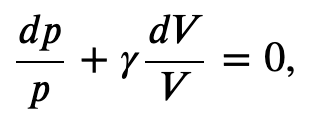
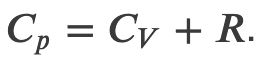
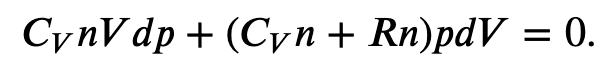
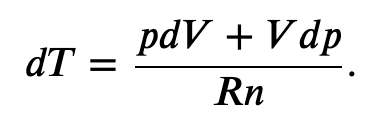
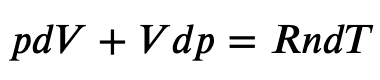
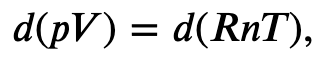
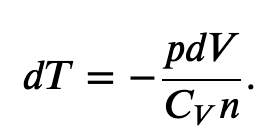
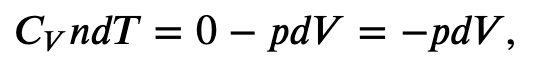
and solving for dT

But we also know from the ideal gas law that

so

and

Now we have two equations for dT, that equating together gives

Which can be written as 

where

and 

Adiabatic Process for an Ideal Gas

Integrating the previous result

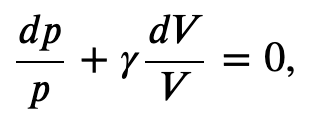
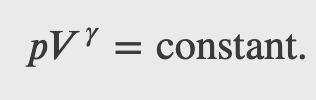
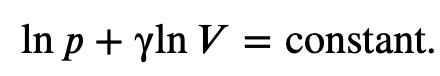
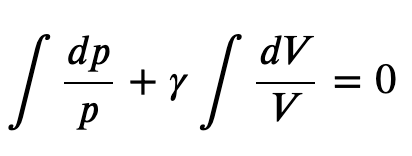
we get

Finally, using ln(𝐴^𝑥)=𝑥ln𝐴 and ln(𝐴𝐵)=ln𝐴+ln𝐵, we can write this in the form

This equation must be obeyed by an ideal gas going through adiabatic process 

Checkpoint

During a thermodynamic process, a system moves from state A to state B, it is supplied with 400 J of heat and does 100 J of work. (a) For this transition, what is the system’s change in internal energy? (b) If the system then moves from state B back to state A, what is its change in internal energy? (c) If in moving from A to B along a different path, 𝑊′𝐴𝐵=400 J of work is done on the system, how much heat does it absorb?

a) 300 J

b) -300 J

c) -100 J

Checkpoint

Consider the quasi-static expansion of an ideal gas between the equilibrium states A and C.  If 515 J of heat are added to the gas as it traverses the path ABC, how much heat is required for the transition along ADC?

Assume that

𝑝_1=2.1×10^5 N/m^2, 𝑉_1=2.25×10^−3 m^3

𝑝_2=1.05×10^5 N/m^2, 𝑉_2=4.5×10^−3 m^3

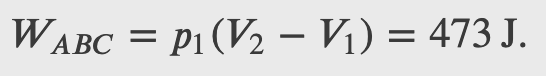
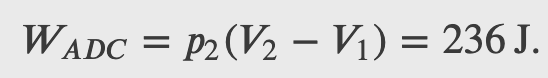
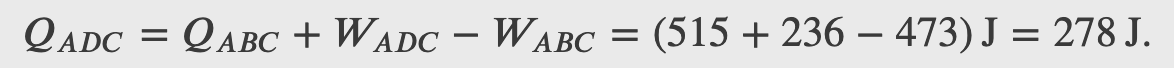
Checkpoint

Heat is added to 1 mol of an ideal monatomic gas confined to a cylinder with a movable piston at one end. The gas expands quasi-statically at a constant temperature of 300 K until its volume increases from V to 3V. (a) What is the change in internal energy of the gas? (b) How much work does the gas do? (c) How much heat is added to the gas?

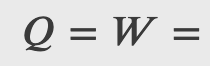
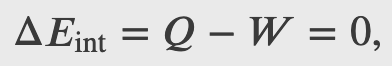
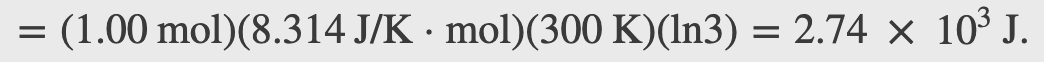
Checkpoint

When 1.00 g of ammonia boils at atmospheric pressure and −33.0°C, its volume changes from 1.47 to 1130cm^3. Its heat of vaporization at this pressure is 1.37×10^6 J/kg. What is the change in the internal energy of the ammonia when it vaporizes?

dE = 1358.7

Checkpoint

A machinist polishes a 0.5 kg copper fitting with a piece of emery cloth for 2 min. He moves the cloth across the fitting at a constant speed of 1 m/s by applying a force of 20 N, tangent to the surface of the fitting. (a) What is the total work done on the fitting by the machinist? (b) What is the increase in the internal energy of the fitting? Assume that the change in the internal energy of the cloth is negligible and that no heat is exchanged between the fitting and its environment. (c) What is the increase in the temperature of the fitting?

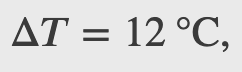
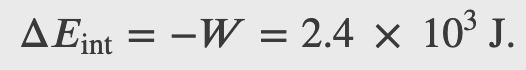
The 2nd Law of Thermodynamics

Heat of itself never flows from a hot object to a cold object

The second law of thermodynamics describes the direction of heat flow in natural processes

When heat flows from one object to another, there is a finite temperature difference (gradient) between the two objects. More importantly, at any given moment of the process, the system most likely is not at equilibrium or in a well-defined state. This phenomenon is called irreversibility.

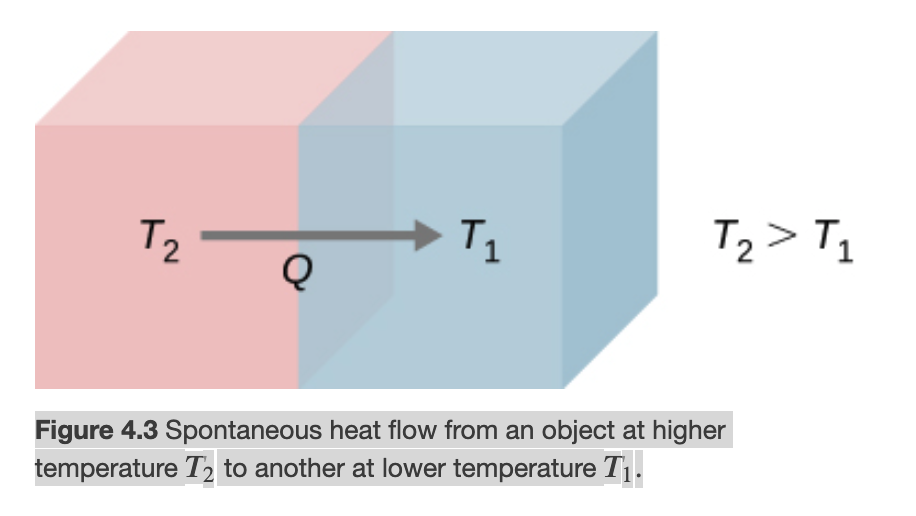
A natural spontaneous process flows in an irreversible path

An irreversible process is what we encounter in reality almost all the time. The system and its environment cannot be restored to their original states at the same time.

Only ideal quasi-static processes are reversible

Heat Engine and Second Law

A heat engine is any device that changes heat energy into mechanical work

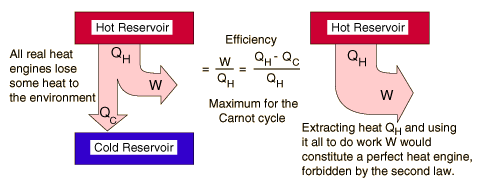
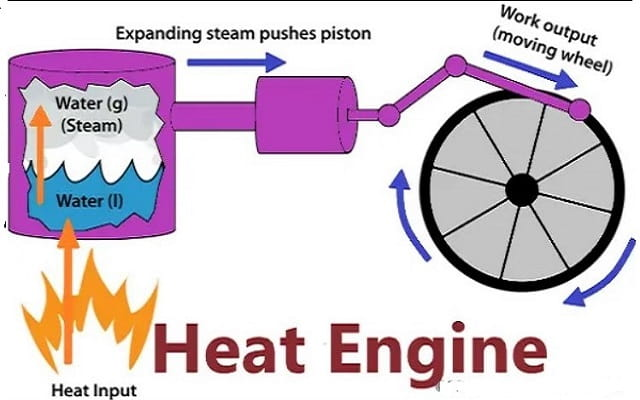
Heat engines operate by carrying a working substance through a cycle. In a steam engine, the working substance is water, which starts as a liquid, becomes vaporized, is then used to move a piston, and is finally condensed back into the liquid state. As is the case for all working substances in cyclic processes, once the water returns to its initial state, it repeats the same sequence.

If we reverse the process of a heat engine we get a heat pump

Heat Pump

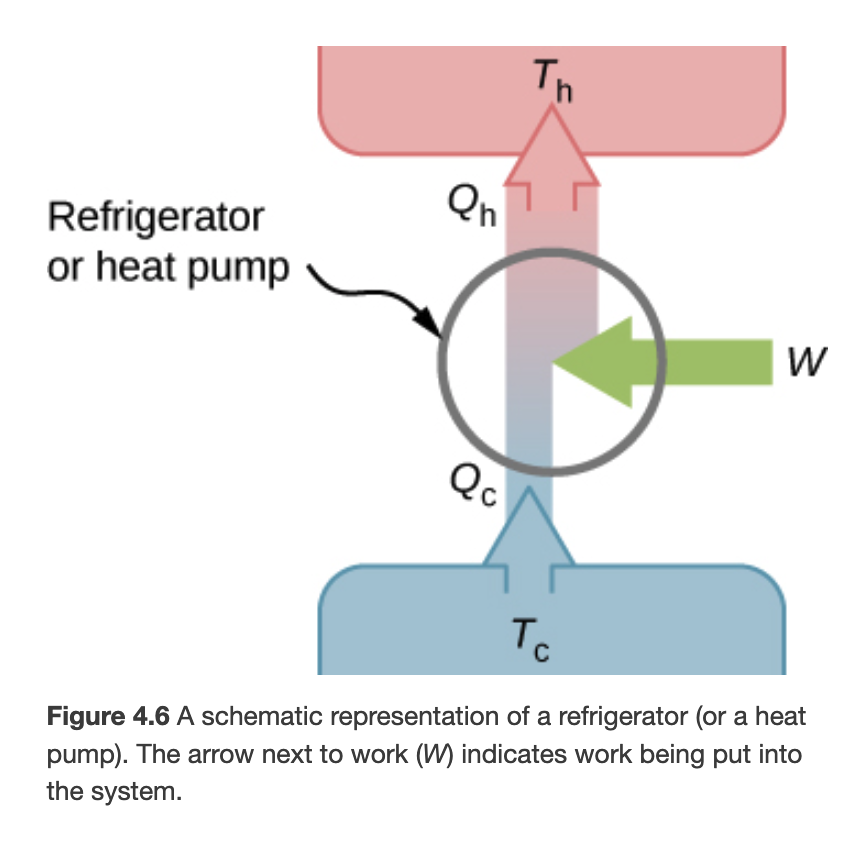
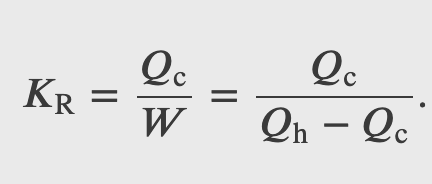
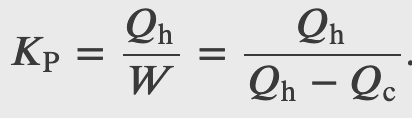
Coefficient of performance

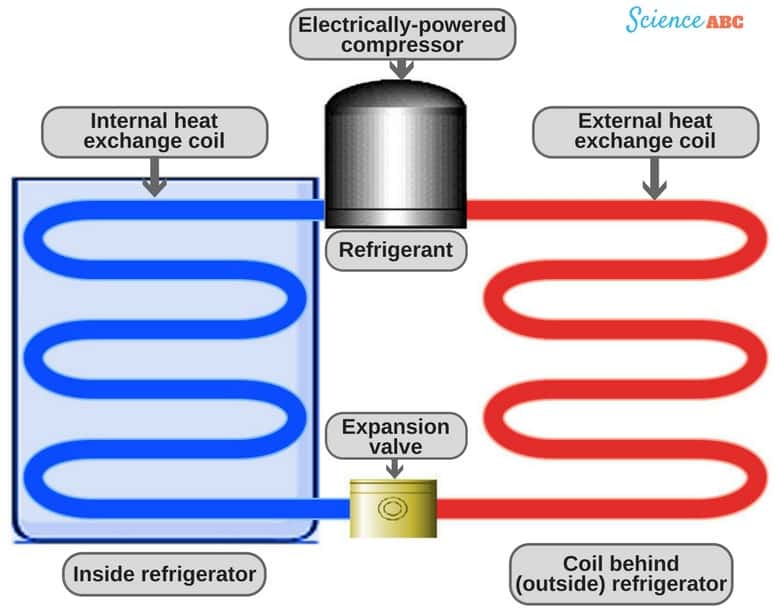
How a Refrigerator Works?

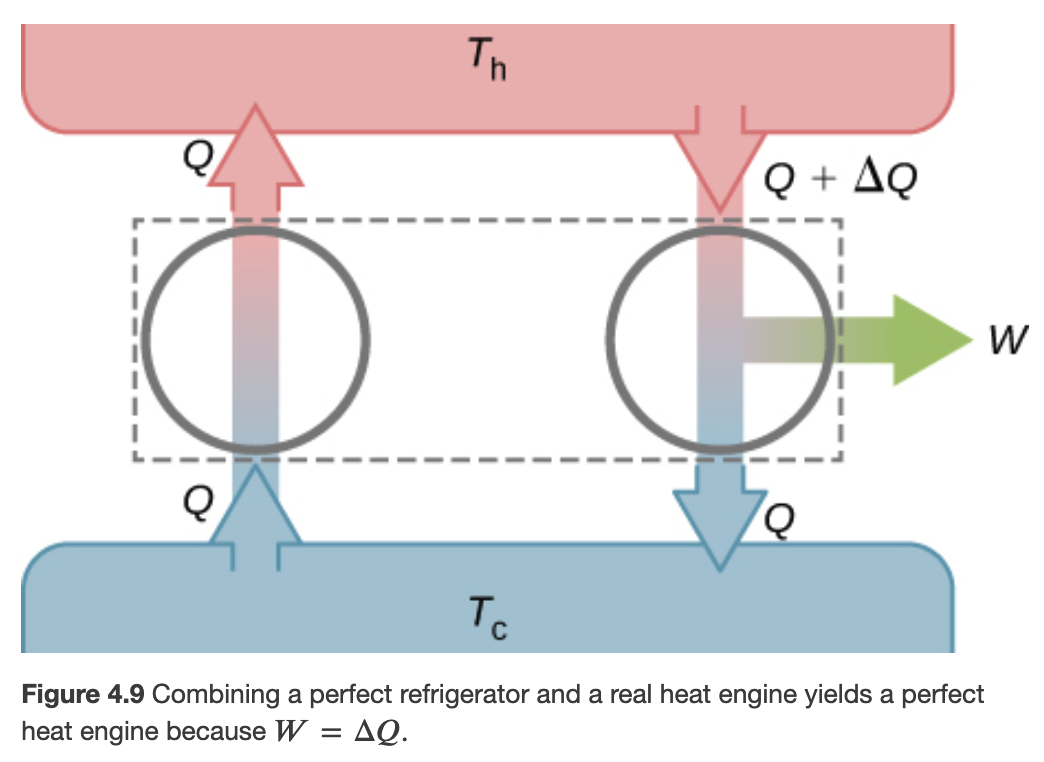
A perfect reversible heat engine would imply heat to flow from cold to hot, which is forbidden by the 2nd law of thermodynamics

Heat Engine and Second Law

It is impossible to convert the heat from a single source into work without any other effect.

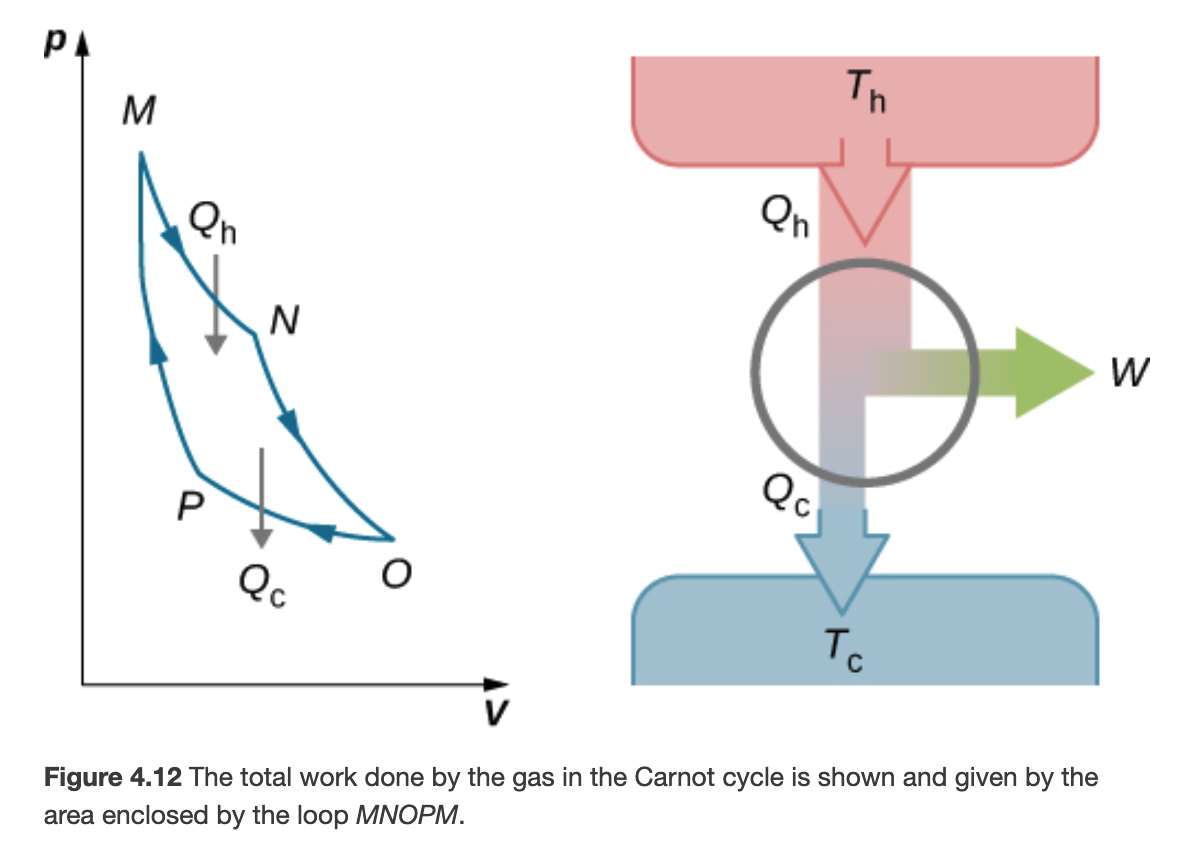
The Carnot Engine Cycle

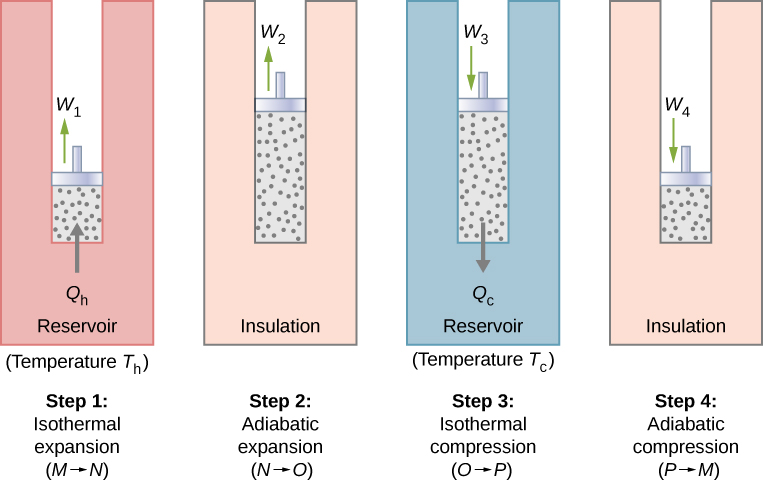
Work and Heat  in a Carnot Cycle

1. Isothermal Expansion (M->N)

2. Adiabatic Expansion (N->O)

3. Isothermal Compression (O->P)

4. Adiabatic Compression (P->M)

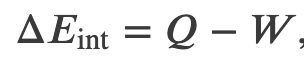
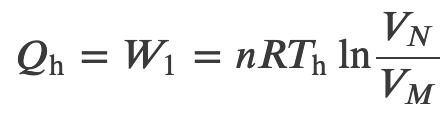
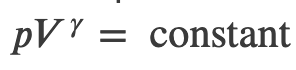
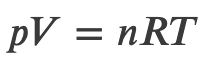
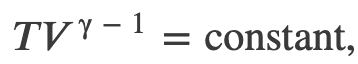
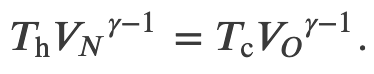
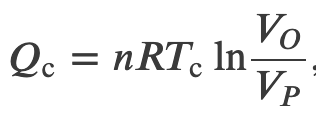
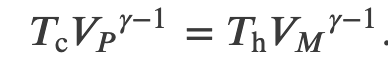
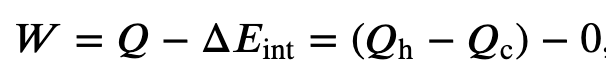
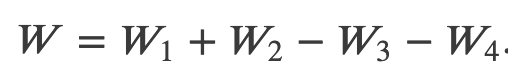
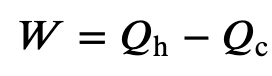
Efficiency of a Carnot Engine

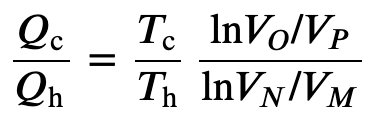
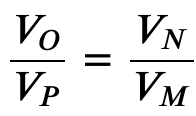
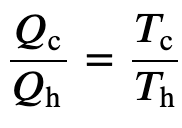
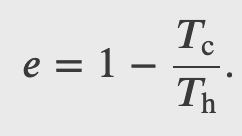
To find the efficiency, we first divide 𝑄c by 𝑄h:

When the adiabatic constant from step 2 is divided by that of step 4, we find

thus

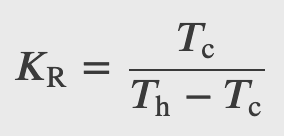
and

No engine working between two reservoirs at constant temperatures can have a greater efficiency than a reversible/carnot engine.

Carnot's Principle

Carnot's principle is another expression of the 2nd law of thermodynamics, it can be summarized as:

Entropy

Entropy

The second law of thermodynamics is best expressed in terms of a change in the thermodynamic variable known as entropy, which is represented by the symbol S. Entropy, like internal energy, is a state function. This means that when a system makes a transition from one state into another, the change in entropy Δ𝑆 is independent of path and depends only on the thermodynamic variables of the two states.

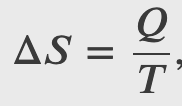
where Q is the heat exchanged by the system kept at a temperature T (in kelvin).

Entropy of a Carnot Engine

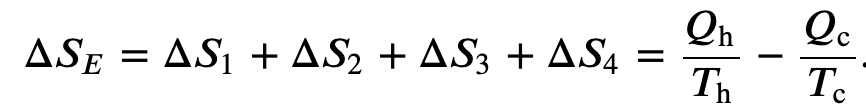
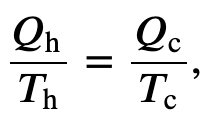
We can find the entropy change of a carnot cycle by adding the entropy change of each step at constant Temperature

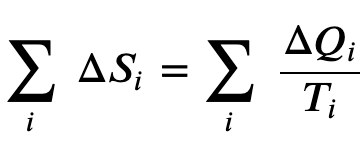
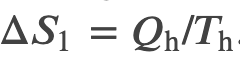
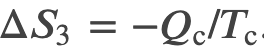
And we know that for a carnot engine 

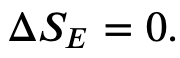
so

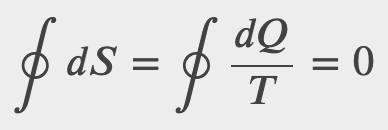
In general for any reversible cycle the change in entropy is 0

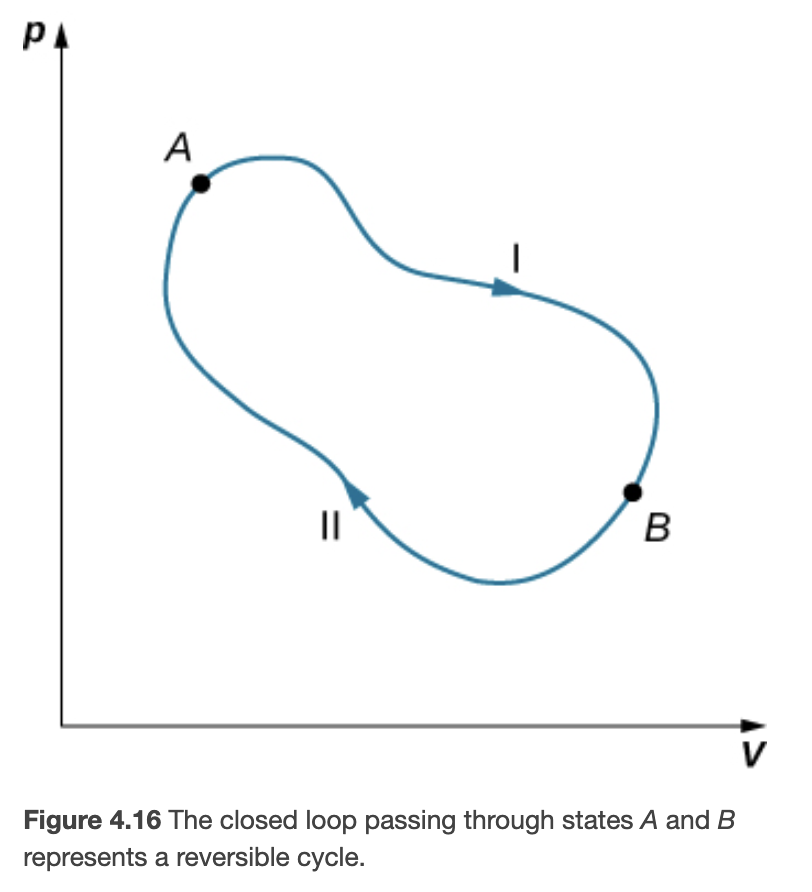
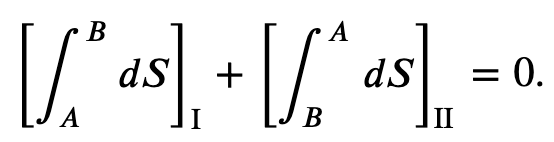
Entropy and The 2nd Law of Thermodynamics 

The entropy of a closed system and the entire universe never decreases.

\Delta S > 0

What is Entropy?

Checkpoint

Heat is slowly added to a 50-g chunk of ice at 0°C until it completely melts into water at the same temperature. What is the entropy change of the ice?

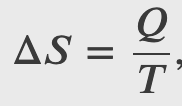
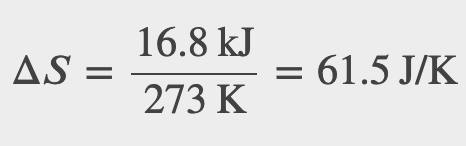
Checkpoint

 

Determine the entropy change of an object of mass m and specific heat c that is cooled rapidly (and irreversibly) at constant pressure from 𝑇_h to 𝑇_c.

\Delta S < 0, \ \text{but} \\ \Delta S_{universe} > 0

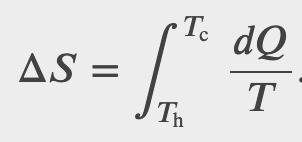
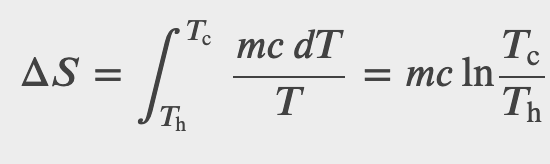
Checkpoint

What is the entropy change in the isothermal expansion of an ideal gas?

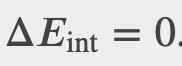
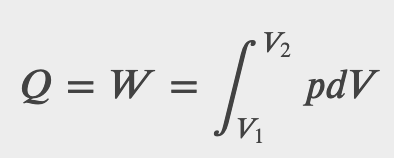
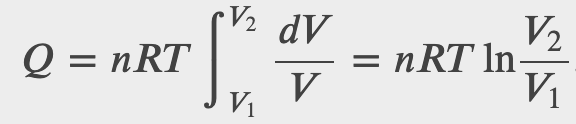
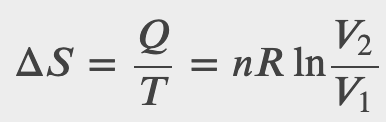
Checkpoint

A 50-g copper piece at a temperature of 20°C is placed into a large insulated vat of water at 100°C. (a) What is the entropy change of the copper piece when it reaches thermal equilibrium with the water? (b) What is the entropy change of the water? (c) What is the entropy change of the universe?

The End