Lección 10: Sistemas LTI en el espacio de estados

BE3024 - Sistemas de Control 1 (Biomédica)

2do ciclo, 2024

Concluyendo nuestro repaso de conceptos matemáticos

\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}
\mathbf{v}=\begin{bmatrix} -1 & 0 & 1 & 2 \end{bmatrix}
\mathbf{w}=\begin{bmatrix} 0.5 & -8 & 1 \end{bmatrix}^\top
x = [1; 2; 3]
v = [-1, 0, 1, 2]
w = [0.5, -8, 1]'
x_2
x(2)
x(1:2)
\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}
x_3
x(end)
\mathbf{x}+\mathbf{w}
x + w
\langle\mathbf{x},\mathbf{w}\rangle
x' * w
\|\mathbf{x}\|_2
norm(x, 2)
\mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}= \begin{bmatrix} 1 & 0 & -1 \\ -2 & 3 & 0 \\ 0 & 0 & -0.5 \end{bmatrix}
A = [1, 0, -1; -2, 3, 0; 0, 0, -0.5]
a_{23}
A(2, 3)
\begin{bmatrix} a_{12} & a_{13} \\ a_{22} & a_{23} \\ a_{32} & a_{33} \end{bmatrix}
A(:, 2:end)
\mathbf{A}^\top
A'
\det(\mathbf{A})
det(A)
\mathbf{I}_{3\times 3}
I = eye(3)
\mathbf{0}_{2\times5}
zeros(2, 5)
\mathbf{A}^{-1}
A^(-1)
I/A
inv(A)
\mathbf{A}\mathbf{I}
A * I
eig(A)
\sigma(\mathbf{A})=\left\{\lambda_1, \lambda_2, \cdots, \lambda_n \right\}
f(\mathbf{x})=f(x_1,x_2,x_3)=x_1^2+\cos(x_2)-e^{-x_3}
syms x1 x2 x3
f(x1, x2, x3) = x1^2 + cos(x2) - exp(-x3)
\nabla f(\mathbf{x})
g = gradient(f)
\mathbf{f}(\mathbf{x})=\begin{bmatrix} f_1(x_1,x_2,x_3) \\ f_2(x_1,x_2,x_3) \end{bmatrix}= \begin{bmatrix} 2x_1-\sin(x_2)-e^{-x_3} \\ x_1^2+\cos(x_2)-x_3 \end{bmatrix}
syms x1 x2 x3
f(x1, x2, x3) = [ 2*x1 - sin(x2) - exp(-x3); 
                  x1^2 + cos(x2) - x3       ]
D\mathbf{f}(\mathbf{x})=\dfrac{d\mathbf{f}(\mathbf{x})}{d\mathbf{x}}
Df = jacobian(f, [x1, x2, x3])
\mathbf{A}(t)=\begin{bmatrix} f_{11}(t) & f_{12}(t) \\ f_{21}(t) & f_{22}(t) \end{bmatrix}= \begin{bmatrix} t^2 & \cos(t) \\ e^{-t} & 1/t \end{bmatrix}
syms t
A(t) = [t^2, cos(t); exp(-t), 1 / t]
\dfrac{d\mathbf{A}(t)}{dt}
dAdt = diff(A)
\displaystyle\int \mathbf{A}(t)dt
intA = int(A)

¿Cómo obtenemos modelos en el espacio de estados?

Directamente desde el modelado

\begin{cases} \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\ \mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u} \\ \mathbf{x}(t_0)=\mathbf{x}_0 \end{cases} 
sys = ss(A, B, C, D)

Directamente desde el modelado

\begin{cases} \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\ \mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u} \\ \mathbf{x}(t_0)=\mathbf{x}_0 \end{cases}

vector de estado \(\mathbf{x}\in\mathbb{R}^n\)

vector de entrada \(\mathbf{u}\in\mathbb{R}^m\)

vector de salida \(\mathbf{y}\in\mathbb{R}^p\)

condición inicial

Directamente desde el modelado

\begin{cases} \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\ \mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u} \\ \mathbf{x}(t_0)=\mathbf{x}_0 \end{cases}

matriz del sistema

\(\mathbf{A}\in\mathbb{R}^{n \times n}\)

términos feedforward

\(\mathbf{D}\in\mathbb{R}^{p \times m}\)

matriz de salida

\(\mathbf{C}\in\mathbb{R}^{p \times n}\)

matriz de control

\(\mathbf{B}\in\mathbb{R}^{n \times m}\)

Directamente desde el modelado

\begin{cases} \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u} \\ \mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u} \\ \mathbf{x}(t_0)=\mathbf{x}_0 \end{cases}

Sistema estrictamente propio

Directamente desde el modelado

\begin{cases} \dot{\mathbf{x}}=\mathbf{A}\mathbf{x}+\mathbf{B}u \\ y=\mathbf{C}\mathbf{x}+\mathbf{D}u \\ \mathbf{x}(t_0)=\mathbf{x}_0 \end{cases}

Sistema SISO (Single-Input Single-Output)

Todo sistema que no es SISO se denomina MIMO (Multiple-Inputs Multiple-Outputs)

Ejemplo: sistemas mecánicos

p_1
p_2
M
(ms^2+k)P_1(s)-kP_2(s)=F_1(s) \\ (Ms^2+Bs+k)P_2(s)-kP_1(s)=F_{iso}(s)
m\ddot{p}_1+kp_1-kp_2=f_1 \\ M\ddot{p}_2+B\dot{p}_2+kp_2-kp_1=f_{iso}
\mathcal{L}^{-1}

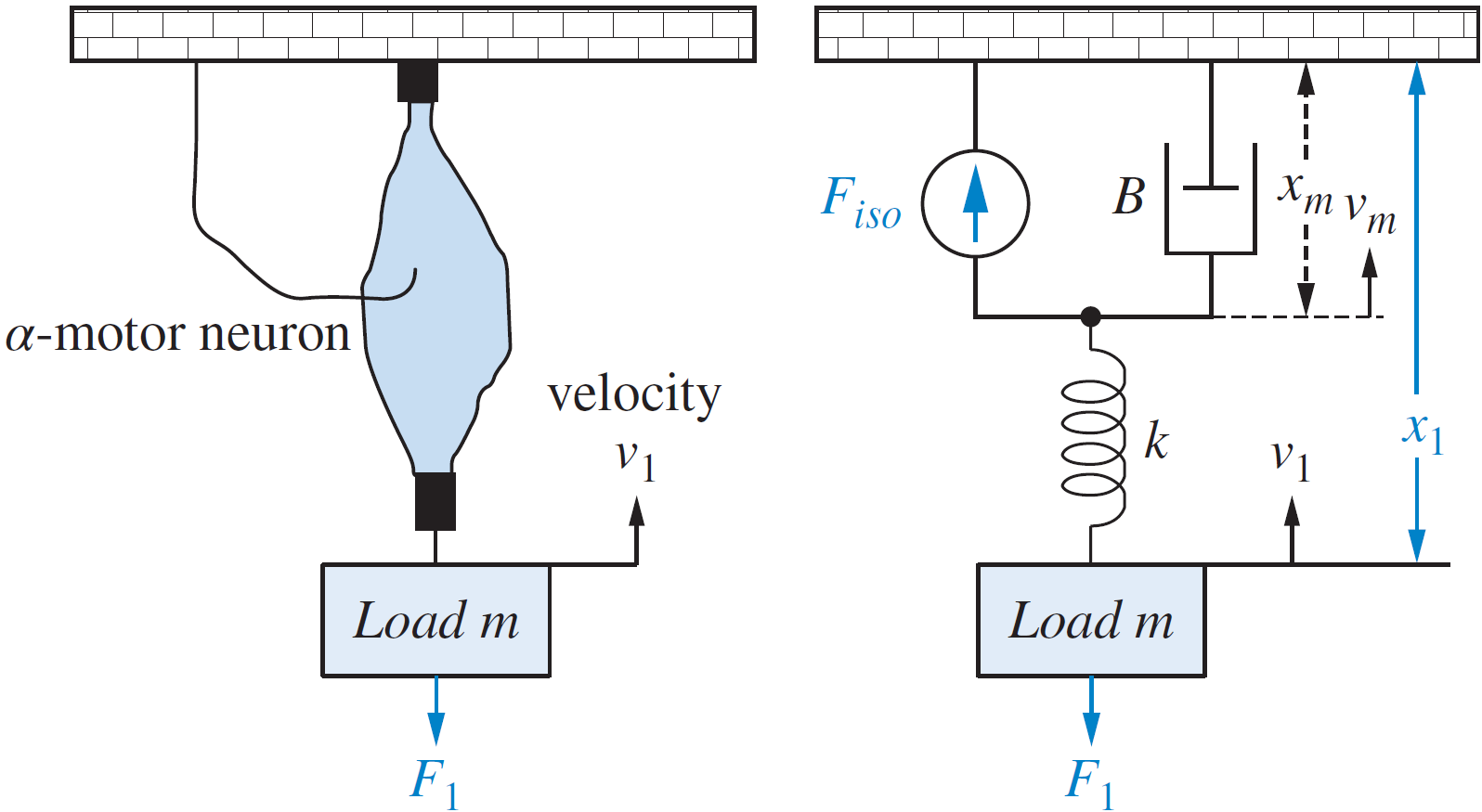
Para sistemas mecánicos, las variables de estado corresponden a las posiciones y velocidades.

\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}=\begin{bmatrix} p_1 \\ p_2 \\ \dot{p}_1 \\ \dot{p}_2 \end{bmatrix}
\mathbf{u}=\begin{bmatrix} u_1 \\ u_2 \end{bmatrix}=\begin{bmatrix} f_1 \\ f_{iso} \end{bmatrix}
\mathbf{y}=y=p_1=x_1
m\ddot{p}_1+kp_1-kp_2=f_1 \\ M\ddot{p}_2+B\dot{p}_2+kp_2-kp_1=f_{iso}

Depende de qué es lo que podemos / queremos medir.

\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}=\begin{bmatrix} p_1 \\ p_2 \\ \dot{p}_1 \\ \dot{p}_2 \end{bmatrix}
\mathbf{u}=\begin{bmatrix} u_1 \\ u_2 \end{bmatrix}=\begin{bmatrix} f_1 \\ f_{iso} \end{bmatrix}
\mathbf{y}=y=p_1=x_1
m\dot{x}_3+kx_1-kx_2=u_1 \\ M\dot{x}_4+Bx_4+kx_2-kx_1=u_2

Depende de qué es lo que podemos / queremos medir.

\dot{x}_3=-\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \dot{x}_4=\frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2
\dot{\mathbf{x}}=\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} \dot{p}_1 \\ \dot{p}_2 \\ \ddot{p}_1 \\ \ddot{p}_2 \end{bmatrix} =\begin{bmatrix} x_3 \\ x_4 \\ -\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2 \end{bmatrix}
\dot{\mathbf{x}}=\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} \dot{p}_1 \\ \dot{p}_2 \\ \ddot{p}_1 \\ \ddot{p}_2 \end{bmatrix} =\begin{bmatrix} x_3 \\ x_4 \\ -\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2 \end{bmatrix}
\dot{x}_3=-\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \dot{x}_4=\frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2
\dot{\mathbf{x}}=\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} \dot{p}_1 \\ \dot{p}_2 \\ \ddot{p}_1 \\ \ddot{p}_2 \end{bmatrix} =\begin{bmatrix} x_3 \\ x_4 \\ -\frac{k}{m}x_1+\frac{k}{m}x_2+u_1 \\ \frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+u_2 \end{bmatrix}
\mathbf{A}\mathbf{x}+\mathbf{B}\mathbf{u}
\begin{bmatrix} x_3 \\ x_4 \\ -\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2 \end{bmatrix}
\dot{x}_3=-\frac{k}{m}x_1+\frac{k}{m}x_2+\frac{1}{m}u_1 \\ \dot{x}_4=\frac{k}{M}x_1-\frac{k}{M}x_2-\frac{B}{M}x_4+\frac{1}{M}u_2
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -k/m & k/m & 0 & 0 \\ k/M & -k/M & 0 & -B/M \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1/m & 0 \\ 0 & 1/M \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}
\dot{\mathbf{x}}
\mathbf{A}
\mathbf{x}
\mathbf{B}
\mathbf{u}

¿Y la otra ecuación?

\mathbf{y}=\mathbf{C}\mathbf{x}+\mathbf{D}\mathbf{u}
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -k/m & k/m & 0 & 0 \\ k/M & -k/M & 0 & -B/M \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1/m & 0 \\ 0 & 1/M \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}
\dot{\mathbf{x}}
\mathbf{A}
\mathbf{x}
\mathbf{B}
\mathbf{u}
y=x_1=\begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix}
\mathbf{x}
\mathbf{C}

No hay \(\mathbf{D}\mathbf{u}\) 

\(\Rightarrow \mathbf{D}=\mathbf{0}_{1\times2}\)

\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \\ \dot{x}_4 \end{bmatrix}=\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -k/m & k/m & 0 & 0 \\ k/M & -k/M & 0 & -B/M \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 1/m & 0 \\ 0 & 1/M \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}
\dot{\mathbf{x}}
\mathbf{A}
\mathbf{x}
\mathbf{B}
\mathbf{u}

Ejemplo: circuitos eléctricos

\imath
\left(R+Ls+\dfrac{1}{sC}\right)I(s)=V_{i}(s)
R\imath+L\dot{\imath}+\dfrac{1}{C}\displaystyle\int_{t_0}^{t}\imath(\tau)d\tau=V_i
\mathcal{L}^{-1}

Para circuitos eléctricos, las variables de estado corresponden a los voltajes en los capacitores y a las corrientes en los inductores.

\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} v_c \\ \imath_L \end{bmatrix}
\mathbf{u}=u=V_i
\mathbf{y}=y=V_o=R\imath
R\imath+L\dot{\imath}+\dfrac{1}{C}\displaystyle\int_{t_0}^{t}\imath(\tau)d\tau=V_i
\Rightarrow R\imath_L+L\dot{\imath}_L+v_C=V_i
\imath
Rx_2+L\dot{x}_2+x_1=u
\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}=\begin{bmatrix} v_c \\ \imath_L \end{bmatrix}
\mathbf{u}=u=V_i
\mathbf{y}=y=V_o=R\imath
R\imath+L\dot{\imath}+\dfrac{1}{C}\displaystyle\int_{t_0}^{t}\imath(\tau)d\tau=V_i
\Rightarrow R\imath_L+L\dot{\imath}_L+v_C=V_i
\imath
\dot{x}_2=-\dfrac{1}{L}x_1-\dfrac{R}{L}x_2+\dfrac{1}{L}u
\dot{\mathbf{x}}=\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=\begin{bmatrix} \dot{v}_C \\ \dot{\imath}_L \end{bmatrix} =\begin{bmatrix} \frac{1}{C}x_2 \\ -\frac{1}{L}x_1-\frac{R}{L}x_2+\frac{1}{L}u \end{bmatrix}
\dot{v}_C = \frac{1}{C}\imath_C = \frac{1}{C}\imath_L = \frac{1}{C}x_2
y=R\imath=Rx_2
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix}=\begin{bmatrix} 0 & 1/C \\ -1/L & -R/L \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ 1/L \end{bmatrix} u
y=Rx_2=\begin{bmatrix} 0 & R \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}
\dot{\mathbf{x}}
\mathbf{A}
\mathbf{x}
\mathbf{B}
\mathbf{u}
\mathbf{x}
\mathbf{C}

A partir de modelos clásicos

Si partimos de \(G(s)=\dfrac{Y(s)}{U(s)}\), encontrar el modelo en espacio de estados es tan simple como:

sys = ss(G)

A partir de modelos clásicos

sys = ss(G)

y aplican las mismas funciones de la Toolbox que antes.

Si partimos de \(G(s)=\dfrac{Y(s)}{U(s)}\), encontrar el modelo en espacio de estados es tan simple como:

A partir de modelos clásicos

si partimos de \(G(s)=\dfrac{Y(s)}{U(s)}\) encontrar el modelo en espacio de estados es tan simple como

sys = ss(G)

y aplican las mismas funciones de la Toolbox que antes.

¿Pero qué es realmente lo que está ocurriendo?

G(s)
u
y
G(s)
u
y
G(s)
u
y

veamos qué hay adentro...

Ejemplo: diagramas de bloques

y^{(3)}-2\ddot{y}-5\dot{y}-6y=u

Ejemplo: diagramas de bloques

y^{(3)}-2\ddot{y}-5\dot{y}-6y=u

Ejemplo: diagramas de bloques

y^{(3)}-2\ddot{y}-5\dot{y}-6y=u

las salidas de los integradores conforman al estado \(\mathbf{x}\)

x_1
x_2
x_3
\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} y \\ \dot{y} \\ \ddot{y} \end{bmatrix}
\mathbf{u}=u
\mathbf{y}=y=x_1
y^{(3)}-2\ddot{y}-5\dot{y}-6y=u
\mathbf{x}=\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} y \\ \dot{y} \\ \ddot{y} \end{bmatrix}
\mathbf{u}=u
\mathbf{y}=y=x_1
\dot{\mathbf{x}}=\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix}=\begin{bmatrix} \dot{y} \\ \ddot{y} \\ y^{(3)} \end{bmatrix} =\begin{bmatrix} x_2 \\ x_3 \\ 6x_1+5x_2+2x_3+u \end{bmatrix}
\dot{x}_3-2x_3-5x_2-6x_1=u
\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 6 & 5 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} u
y=x_1=\begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}
\dot{\mathbf{x}}
\mathbf{A}
\mathbf{x}
\mathbf{B}
\mathbf{u}
\mathbf{x}
\mathbf{C}

Algunas observaciones fundamentales

y^{(3)}-2\ddot{y}-5\dot{y}-6y=u
\Rightarrow G(s)=\dfrac{Y(s)}{U(s)}=\dfrac{1}{s^3-2s^2-5s-6}
G = tf(1, [1, -2, -5, -6]);
sys = ss(G)
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 2 & 2.5 & 1.5 \\ 2 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0.5 \\ 0 \\ 0 \end{bmatrix}u\\ y = \begin{bmatrix} 0 & 0 & 0.5 \end{bmatrix}\mathbf{x} \end{cases}
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 2 & 2.5 & 1.5 \\ 2 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0.5 \\ 0 \\ 0 \end{bmatrix}u\\ y = \begin{bmatrix} 0 & 0 & 0.5 \end{bmatrix}\mathbf{x} \end{cases}
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 6 & 5 & 2 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}u\\ y = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\mathbf{x} \end{cases}

del ejemplo anterior

"a mano"

\boldsymbol{\neq}
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 2 & 2.5 & 1.5 \\ 2 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0.5 \\ 0 \\ 0 \end{bmatrix}u\\ y = \begin{bmatrix} 0 & 0 & 0.5 \end{bmatrix}\mathbf{x} \end{cases}
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 6 & 5 & 2 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}u\\ y = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\mathbf{x} \end{cases}

del ejemplo anterior

"a mano"

\boldsymbol{\neq}

¿Cuál es el modelo correcto?

 

\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 2 & 2.5 & 1.5 \\ 2 & 0 & 0 \\ 0 & 2 & 0 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0.5 \\ 0 \\ 0 \end{bmatrix}u\\ y = \begin{bmatrix} 0 & 0 & 0.5 \end{bmatrix}\mathbf{x} \end{cases}
\begin{cases} \dot{\mathbf{x}}= \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 6 & 5 & 2 \end{bmatrix}\mathbf{x}+\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}u\\ y = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\mathbf{x} \end{cases}

del ejemplo anterior

"a mano"

\boldsymbol{\neq}

¿Cuál es el modelo correcto?

¡Ambos! Son distintas realizaciones del mismo sistema.

Dos sistemas son equivalentes si producen la misma función de transferencia.

\mathbf{G}(s)=\mathbf{C}\left(s\mathbf{I}-\mathbf{A}\right)^{-1}\mathbf{B}+\mathbf{D} \qquad \in\mathbb{R}^{p \times m}
sys = ss(A, B, C, D);
G = tf(sys)

Polos y estabilidad

\text{polos} \equiv \sigma(\mathbf{A}) \equiv \text{eigenvalores de }\mathbf{A}
sys = ss(A, B, C, D);
pole(sys)

Resulta que

luego de lo cual aplican los mismos* criterios que en control clásico.

mismos*, aunque podemos ser más específicos:

Marginalmente/críticamente estable requiere que los polos con \(\mathrm{Re}(\lambda)=0\) tengan multiplicidad algebráica unitaria.

 

Para este caso también \(\displaystyle\lim_{t\to\infty} \mathbf{x}(t) \in \mathcal{N}\left(\mathbf{A}\right)\).