
BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
Lección 11: Control de sistemas LTI multivariable
¿Cómo se ve el control en el espacio de estados?
Un ejemplo clave
modelo mínimo de Bergman
glucemia \(y(t)\)
tasa de ingreso de insulina
ingesta de glucosa
control PID
glucemia basal saludable \(r(t)\)
¿Qué ocurre con la glucemia conforme avanza el tiempo?
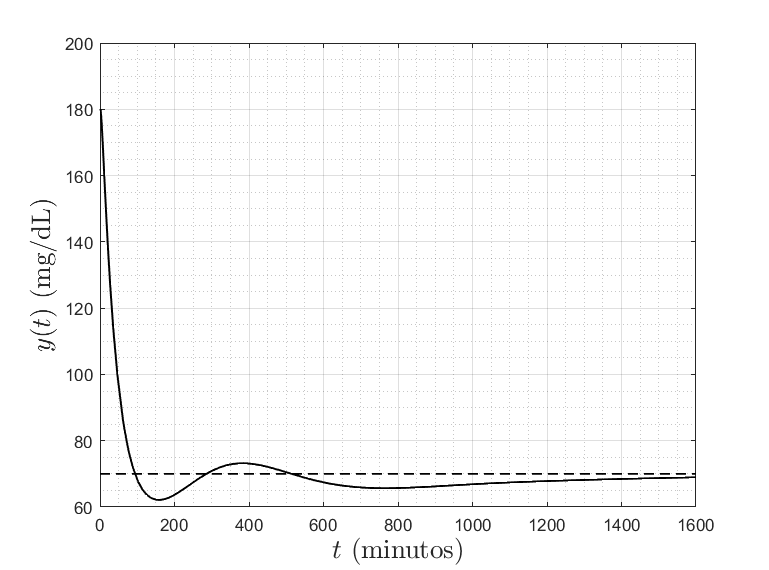

la salida rastrea a la referencia

la salida rastrea a la referencia
Como ahora sabemos, esto no corresponde a la perspectiva completa.

la salida rastrea a la referencia
Como ahora sabemos, esto no corresponde a la perspectiva completa.
¿Qué ocurre con el estado del sistema?
modelo mínimo de Bergman
glucemia \(y(t)\)
tasa de ingreso de insulina
ingesta de glucosa
control PID
glucemia basal saludable \(r(t)\)
¿Qué ocurre internamente en el sistema?
¿Cómo evolucionan las variables de estado conforme la salida rastrea a la referencia?
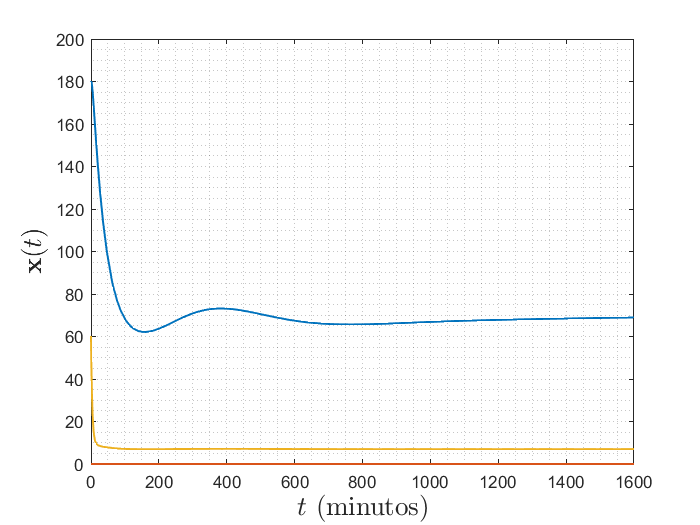
¿Qué podemos observar?

¿Qué podemos observar?
condiciones iniciales distintas a cero

¿Qué podemos observar?
Pareciera que \(y(t)=x_1(t)\), por lo que \(x_1(t)\) está rastreando a \(r(t)\).

¿Qué podemos observar?
\(x_2(t)\) y \(x_3(t)\) también están llegando a cierto valor,
pero no se sabe cuál es o de dónde salió.

¿De qué otra forma podemos describir el comportamiento de las variables de estado sin hablar del valor al cual están llegando?

¿De qué otra forma podemos describir el comportamiento de las variables de estado sin hablar del valor al cual están llegando?

¿De qué otra forma podemos describir el comportamiento de las variables de estado sin hablar del valor al cual están llegando?

¿De qué otra forma podemos describir el comportamiento de las variables de estado sin hablar del valor al cual están llegando?
Las variables de estado dejan de evolucionar
\(\equiv\) las variables de estado se estabilizan
\(\equiv\) se estabiliza el estado.
En el espacio de estados, las consecuencias del control son la estabilización del estado y el rastreo de referencias en la salida.
Parte I: Estabilización de estado
En esencia, la estabilización de estado implica
lo cual se garantiza al hacer que el sistema
sea asintóticamente estable.
En esencia, la estabilización de estado implica
lo cual se garantiza al hacer que el sistema
sea asintóticamente estable.
Todos los eigenvalores de \(\mathbf{A}\) deben estar en el lado izquierdo del plano complejo.
La estrategia principal en el espacio de estados implica utilizar retroalimentación de estado.
Esto transforma la ecuación de estado.
La estrategia principal en el espacio de estados implica utilizar retroalimentación de estado.
Esto transforma la ecuación de estado.
matriz de constantes
Para sistemas LTI, la estabilización de estado se reduce a seleccionar los valores de \(\mathbf{K}\) tal que todos los eigenvalores de \(\mathbf{A}_{c\ell}\) se encuentren en el lado izquierdo del plano complejo.
De forma manual mediante pole placement.
Dos técnicas para estabilización
De forma automática mediante el Regulador Lineal Cuadrático (LQR).
sys = ss(A, B, C, D);K = place(sys.A, sys.B, p)K = lqr(sys.A, sys.B, Q, R)Dos técnicas para estabilización
De forma manual mediante pole placement.
De forma automática mediante el Regulador Lineal Cuadrático (LQR).
sys = ss(A, B, C, D);K = place(sys.A, sys.B, p)K = lqr(sys.A, sys.B, Q, R)CUIDADO, esto funcionará si y sólo si el sistema es completamente controlable (C.C.).
Un sistema LTI es completamente controlable si y sólo si su matriz de controlabilidad
Controlabilidad
tiene rango
Gamma = ctrb(sys)rank(Gamma)igual al orden (número de variables de estado = \(n\)) del sistema.
Ambas técnicas emplean la siguiente arquitectura:
Regresando a estabilización
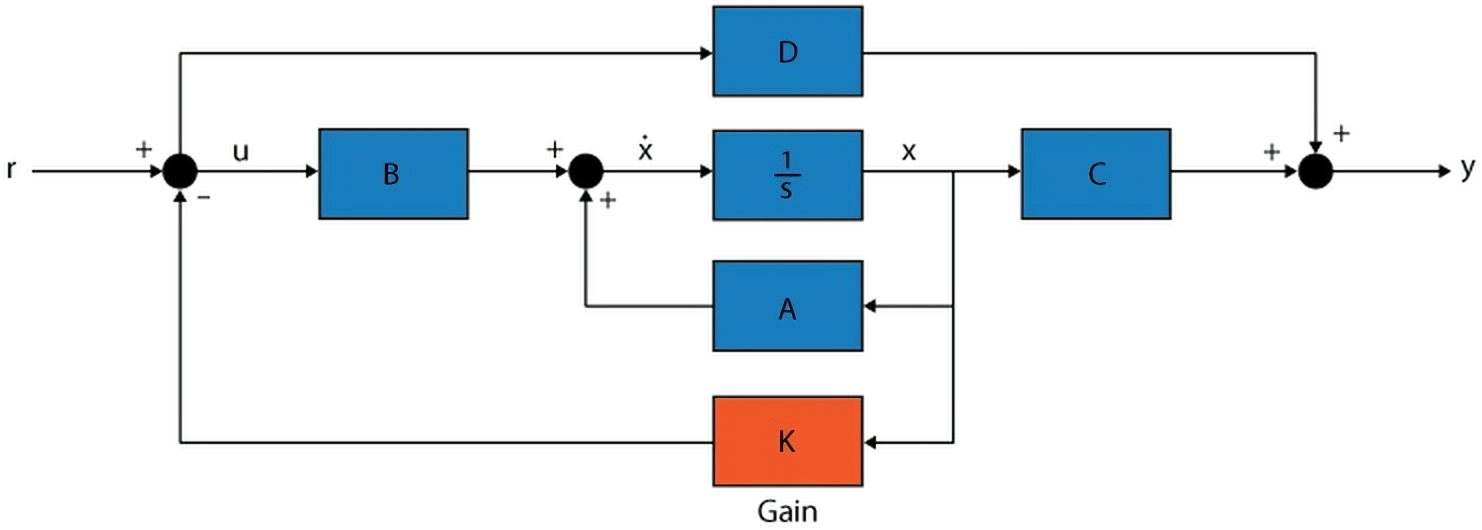
sistema
¿Cómo pueden seleccionarse estos polos deseados? Mediante regiones de diseño.
Pole placement
Nota: el algoritmo no permite que dos polos sean exactamente iguales. Ej: {-1, -1} vs {-1, -1.01}.
K = place(sys.A, sys.B, p)vector de \(n\) polos deseados
Región donde se cumple con los requerimientos.
Región donde se cumple con los requerimientos.
Región donde se cumple con los requerimientos.
Ejemplo: pole placement
Estabilice el sistema, garantizando un tiempo de subida menor a 1 segundo y un overshoot menor al 10%.
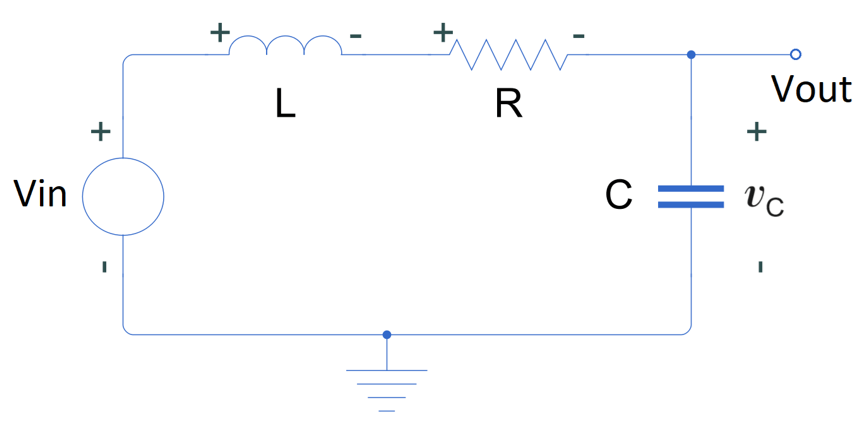
Ejemplo: pole placement
Listado de tareas:
- Encontrar el modelo del sistema.
- Verificar estabilidad.
- Verificar controlabilidad.
- Encontrar polos deseados.
- Encontrar \(\mathbf{K}\) mediante pole placement.
- Crear un nuevo sistema con el control aplicado.
- Evaluar el rendimiento (polos nuevos y respuesta al escalón).
>> clase11_ejemplo_poleplacement.m
Ejemplo: pole placement
Listado de tareas:
- Encontrar el modelo del sistema.
- Verificar estabilidad.
- Verificar controlabilidad.
- Encontrar polos deseados.
- Encontrar \(\mathbf{K}\) mediante pole placement.
- Crear un nuevo sistema con el control aplicado.
- Evaluar el rendimiento (polos nuevos y respuesta al escalón).
¿Qué ocurrió? Los polos se colocaron correctamente pero hay algo raro con el comportamiento en estado estacionario.
¿Qué pasa si se escogen otros polos?
Regulador Lineal Cuadrático (LQR)
Se recomienda iniciar con la matrices identidad e ir modificando los valores de la diagonal para penalizar el comportamiento no deseado en variables de estado y entradas/controles específicas.
K = lqr(sys.A, sys.B, Q, R)matriz de penalización de estado \(\mathbf{Q}\in\mathbb{R}^{n \times n}\)
matriz de penalización de control \(\mathbf{R}\in\mathbb{R}^{m\times m}\)
Regulador Lineal Cuadrático (LQR)
A valores más altos, más se penaliza.
penalización para \(x_2\)
Regulador Lineal Cuadrático (LQR)
A valores más altos, más se penaliza.
penalización para \(u_1\)
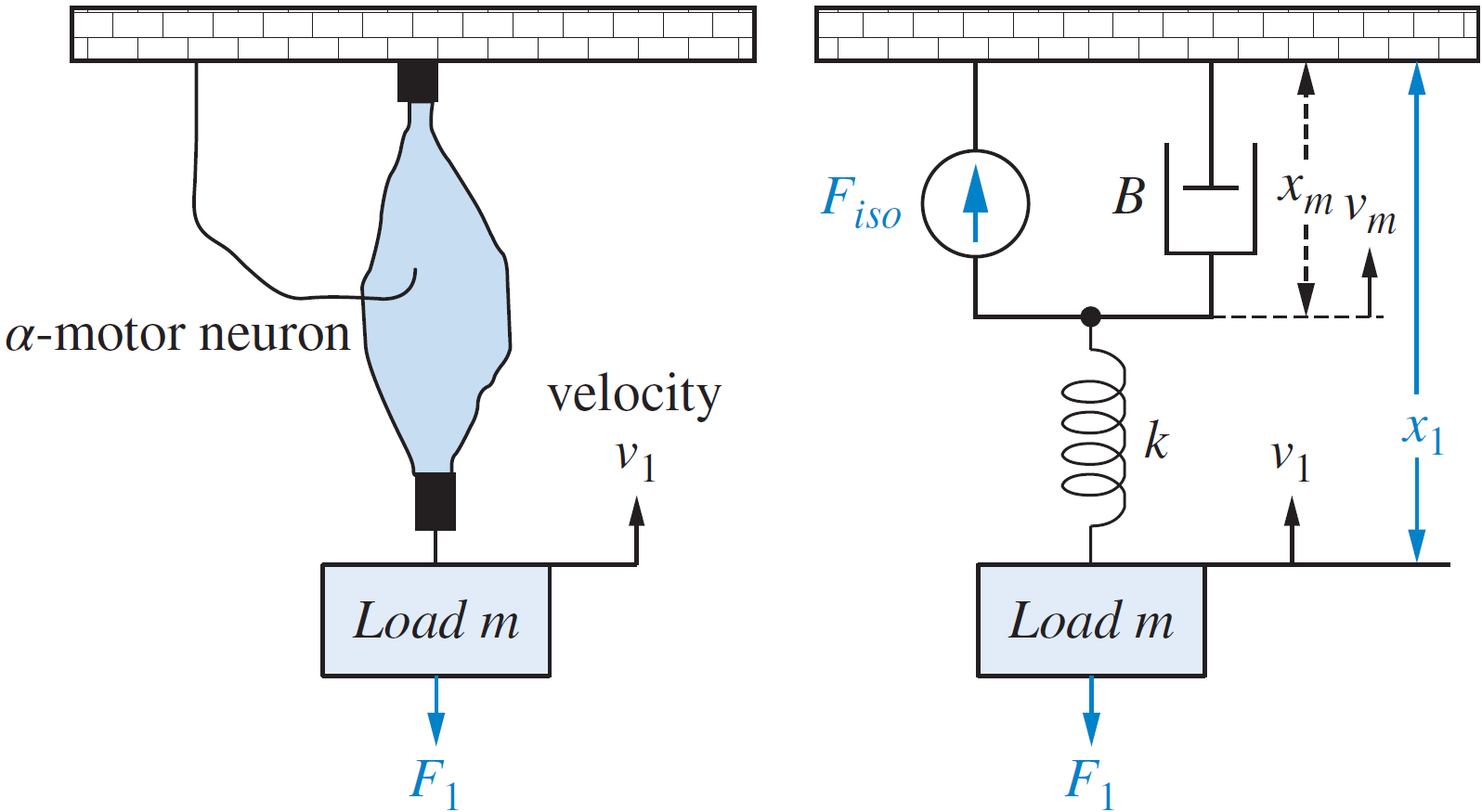
Ejemplo: LQR
Estabilice mediante el regulador lineal cuadrático.
Ejemplo: LQR
Listado de tareas:
- Encontrar el modelo del sistema.
- Verificar estabilidad.
- Verificar controlabilidad.
- Establecer las matrices de penalización.
- Encontrar \(\mathbf{K}\) mediante LQR.
- Crear un nuevo sistema con el control aplicado.
- Evaluar el rendimiento.
>> clase11_ejemplo_lqr.m
Ejemplo: LQR
Listado de tareas:
- Encontrar el modelo del sistema.
- Verificar estabilidad.
- Verificar controlabilidad.
- Establecer las matrices de penalización.
- Encontrar \(\mathbf{K}\) mediante LQR.
- Crear un nuevo sistema con el control aplicado.
- Evaluar el rendimiento.
De nuevo, la respuesta en estado estable se comportó extraño.
Conclusión: debe considerarse el rastreo además de la estabilización.
Nota: en el laboratorio aprenderemos un "truco" que puede servir para ajustar el error en estado estacionario (en ciertos casos), sin usar el rastreo explícitamente como veremos más adelante.
Implementación
Regresemos a la primera solución para el ejemplo del circuito.
K = [4, 3]¿Qué implica esto?
Una simple combinación lineal, versus una ecuación de diferencias "complicada" para el PID.
Implementación
Esto, sin embargo, asume que tenemos acceso a las variables de estado del sistema (!!!)
Implementación
Una simple combinación lineal, versus una ecuación de diferencias "complicada" para el PID.
Parte II: Rastreo de referencias
Fuimos capaces de estabilizar el estado
Fuimos capaces de estabilizar el estado
empleando retroalimentación de estado.
Fuimos capaces de estabilizar el estado
¿Qué hace falta?
empleando retroalimentación de estado.
Fuimos capaces de estabilizar el estado
Que la salida rastree a la referencia.
empleando retroalimentación de estado.
Para lograr esto se requiere estabilizar el error
Es decir, el rastreo de referencias se hace mediante la estabilización del error.
Para lograr esto se requiere estabilizar el error
Es decir, el rastreo de referencias se hace mediante la estabilización del error.
\(\Rightarrow\) dos problemas de estabilización
Estabilizar estado + estabilizar error
Estabilizar estado + estabilizar error
Estabilizar estado + estabilizar error
Estabilizar estado + estabilizar error
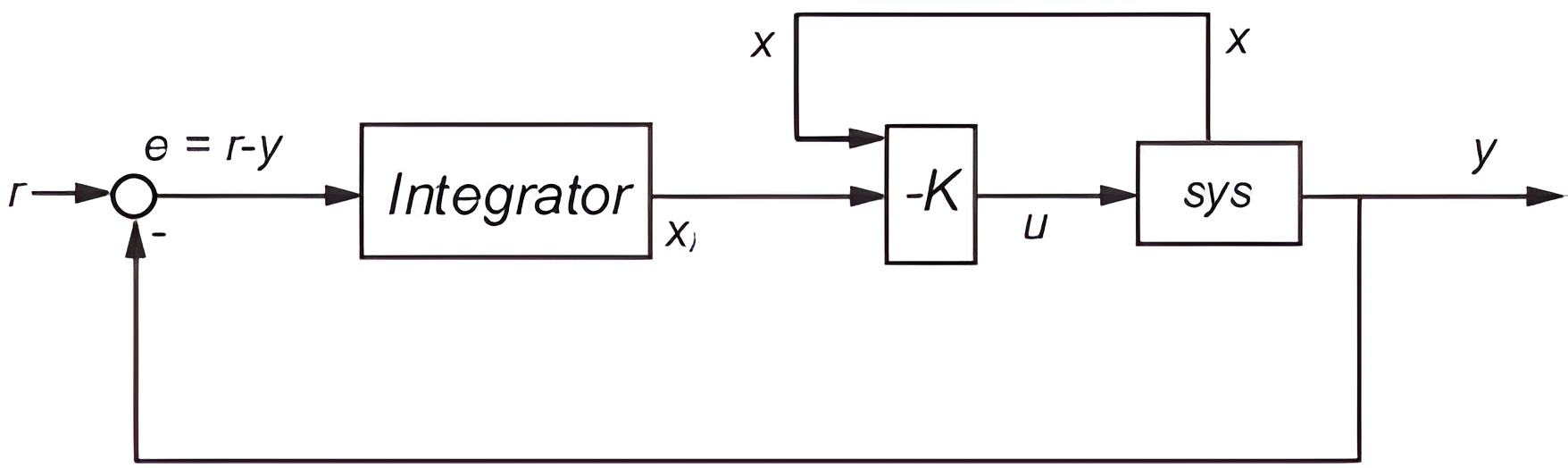
Regulador Cuadrático Integral (LQI)
sys = ss(A, B, C, D);
sys_ext = ss(AA, BB, CC, D);Regulador Lineal Cuadrático Integral (LQI)
sys = ss(A, B, C, D);
sys_ext = ss(AA, BB, CC, D);KK = lqi(sys, QQ, R)
KK = lqr(sys_ext.A, sys_ext.B, QQ, R)sys = ss(A, B, C, D);
sys_ext = ss(AA, BB, CC, D);Regulador Lineal Cuadrático Integral (LQI)
KK = lqi(sys, QQ, R)
KK = lqr(sys_ext.A, sys_ext.B, QQ, R)sys = ss(A, B, C, D);
sys_ext = ss(AA, BB, CC, D);Regulador Lineal Cuadrático Integral (LQI)
i

i
Acl = AA - BB*KK;
sys_cl = ss(Acl, MM, CC, [])
i
Acl = AA - BB*KK;
sys_cl = ss(Acl, MM, CC, [])>> clase11_ejemplo_lqi.m