Lección 2: Sistemas SISO LTI en el dominio de la frecuencia

BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
¿Por qué?
referencia
planta
sensor
controlador
salida
retroalimentación negativa
referencia
planta
sensor
controlador
salida
retroalimentación negativa
entrada
referencia
planta
sensor
controlador
salida
retroalimentación negativa
entrada
sistema SISO LTI
¿Qué implica esto?
TODO sistema LTI puede expresarse como una EDO lineal de coeficientes constantes que relaciona a su salida con su entrada.
Ejemplo
LTI \(\Rightarrow\) EDO lineal con coeficientes constantes
una entrada y una salida \(\Rightarrow\) SISO
(single input single output)
Los sistemas LTI presentan respuestas típicas a señales "estándar".
señal (de prueba) estándar
respuesta típica
escalón
impulso
Escalón unitario
respuesta al escalón
Impulso unitario | delta de Dirac
respuesta impulsional
Respuesta en el tiempo de un sistema LTI (convolución):
Respuesta de un sistema LTI (Laplace):
Función de transferencia:
planta
entrada
salida
Continuando con el ejemplo
¿Cuál es la respuesta en el tiempo del sistema si la entrada es el escalón unitario?
¿Cuál es la función de transferencia del sistema?
Función de transferencia
Respuesta al escalón
Análisis en Matlab
G = tf(10, [1, 8, 12])
step(G); % Respuesta al escalón
impulse(G); % Respuesta impulsional
linearSystemAnalyzer(G); % Permite
% hacer varios análisisejemplo_analisis.m
¿Y si quisiéramos la respuesta a otra entrada?
t = 0:0.01:5;
u = exp(-t);
lsim(G, u, t);¿Qué ocurre al interconectar múltiples sistemas?
sensor
controlador
planta
salida
referencia
diagramas de bloques
Reflejo de estiramiento muscular
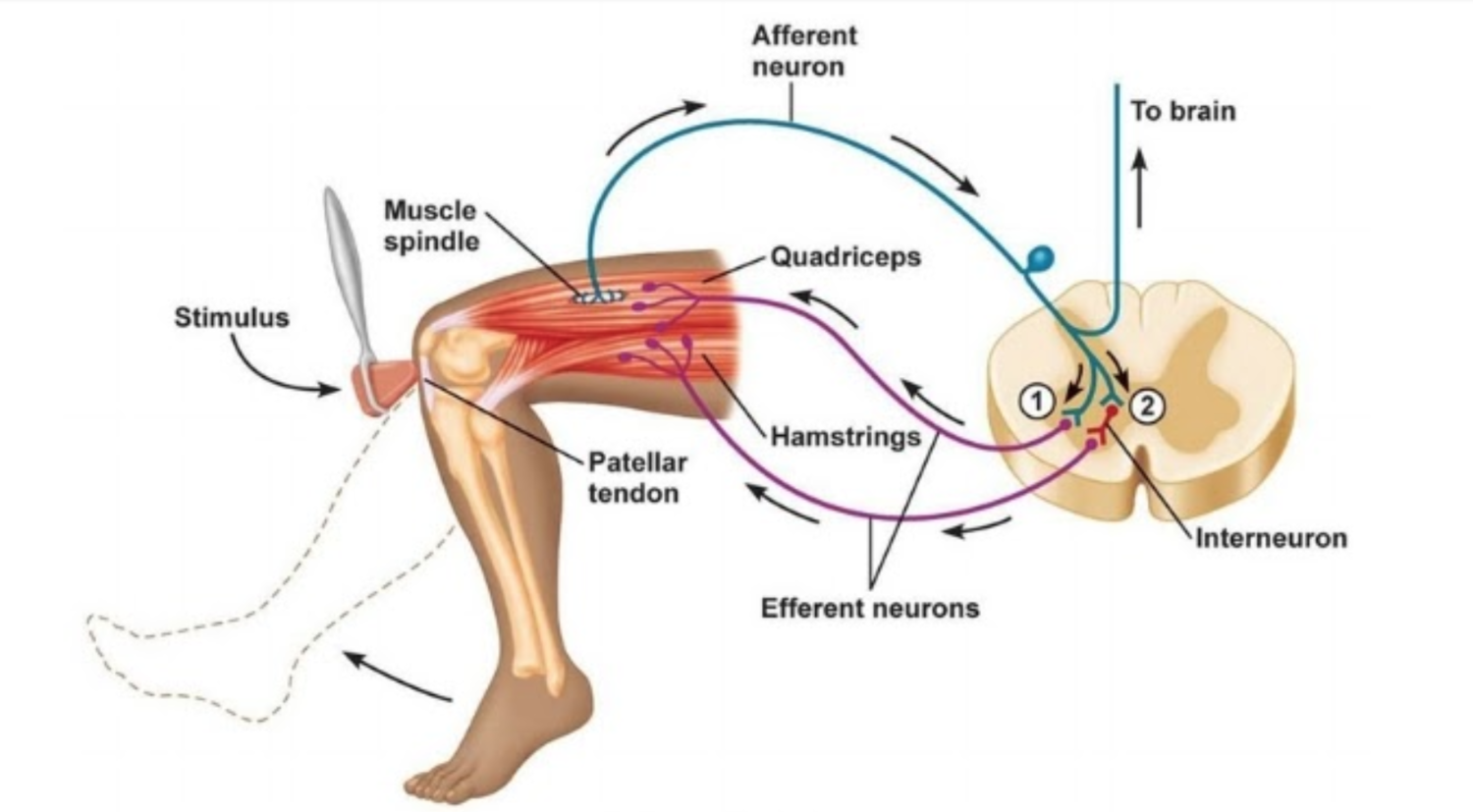
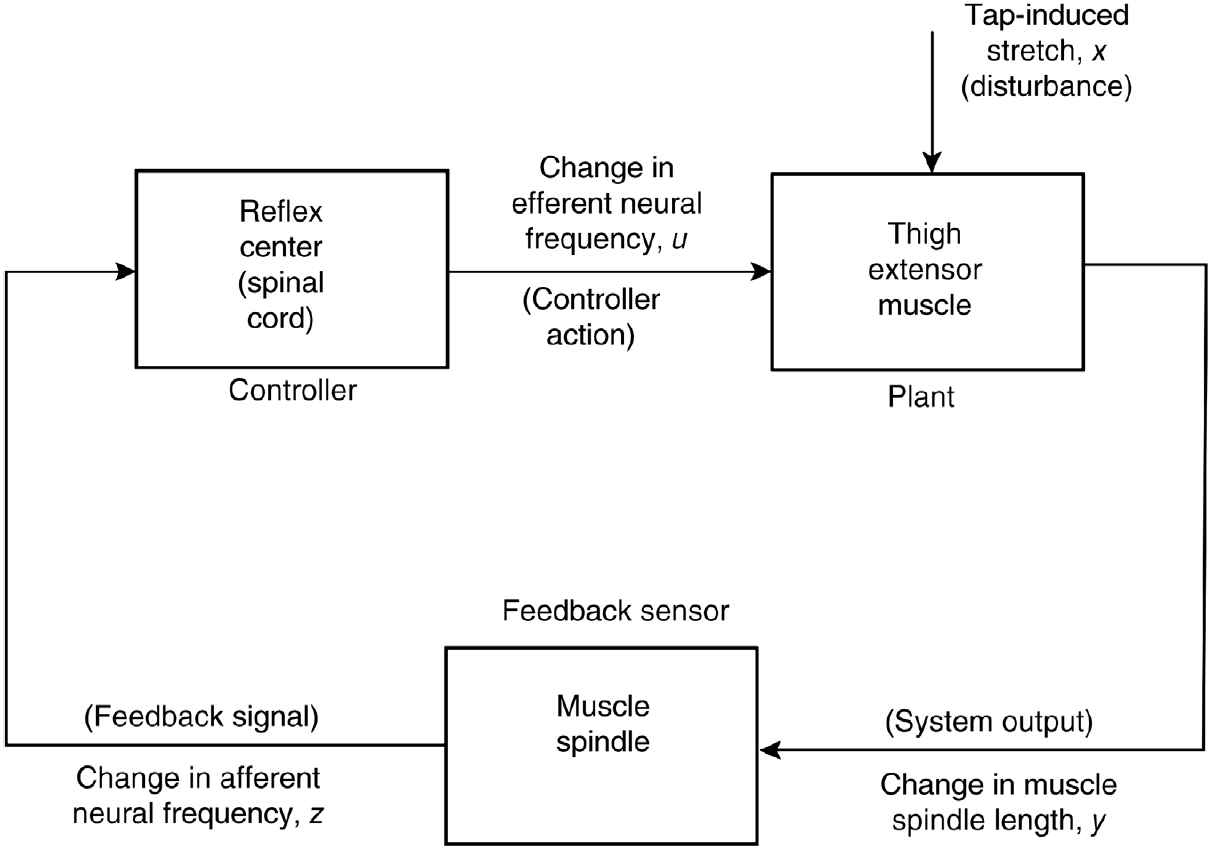
\(\big\uparrow\) representación real e intuición
\(\big\downarrow\) facilidad de análisis
diagramas de bloques
¿Cómo retomamos la facilidad de análisis?
Álgebra de bloques
Reglas fundamentales
Conexión en serie | cascada
Geq = G1 * G2Conexión en paralelo
Geq = G1 + G2Retroalimentación negativa
Geq = feedback(G1, G2)¿Puede demostrarlo?
Ejemplo: Encuentre el equivalente en lazo abierto del siguiente diagrama de bloques.
Simplificación y análisis en Matlab (Control Systems Toolbox)
ejemplo_bloques.m
sensor
controlador
planta
salida
referencia
Regresando al lazo de control canónico
\(E(s)\)
error
\(U(s)\)
Equivalente en lazo abierto