Lección 6: Análisis de la respuesta estacionaria y transitoria

BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
¿Por qué?
plano \(s\)
plano \(s\)
dominio manipulación (frecuencia)
\(\ne\) dominio análisis (tiempo)
plano \(s\)
plano \(s\)
respuesta transitoria
(corto plazo)
respuesta estacionaria
(largo plazo)
ceros: valores de \(s\) que hacen \(N(s)=0\)
polos: valores de \(s\) que hacen \(D(s)=0\)
Polos y ceros
Polos y ceros
ceros: valores de \(s\) que hacen \(N(s)=0\)
polos: valores de \(s\) que hacen \(D(s)=0\)
Los sistemas del mundo real son propios*
adicionalmente
\(\mathrm{grado}\left(D(s)\right)\) \(\equiv\) # polos del sistema
\(\equiv\) orden del sistema
Encuentre los polos y ceros del sistema
Encuentre los polos y ceros del sistema
G = tf([1, 5], [1, 1, -2])
polos = pole(G)
ceros = zero(G)
pzplot(G) % pole-zero plot
grid¿Qué ocurre si \(u(t)=\mathbf{1}(t)\)?
¿Qué ocurre si \(u(t)=\mathbf{1}(t)\)?
¿Qué ocurre si \(u(t)=\mathbf{1}(t)\)?
entrada
sistema
La respuesta de un sistema LTI tiene la forma:
respuesta natural
respuesta forzada
Los sistemas LTI presentan un número limitado de términos (modos) en la respuesta natural.
polo
tiempo
frecuencia
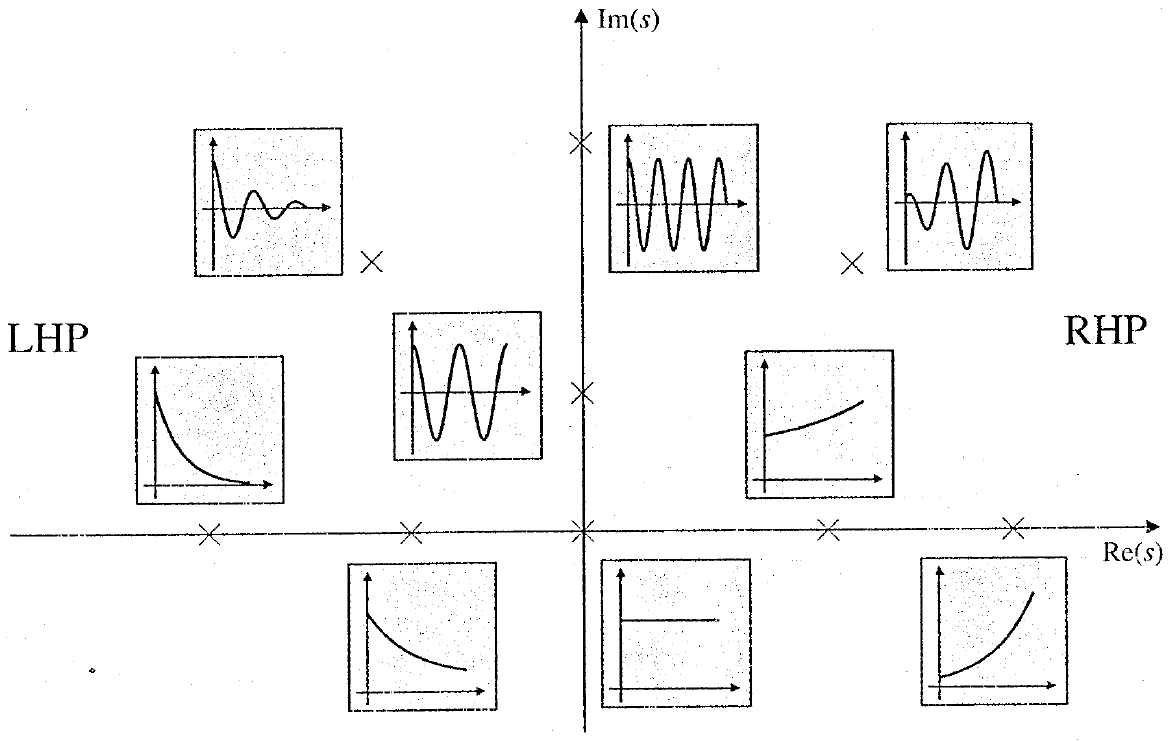
Respuesta estacionaria
Estabilidad
El sistema es:
\((i)\) (asintóticamente) estable
Todos los polos se encuentran en el LHP.
\((ii)\) inestable
Por lo menos un polo está en el RHP.
\((iii)\) marginalmente | críticamente estable
(Asintóticamente) estable pero con un polo real en el origen o un par de polos imaginarios conjugados.
Ejemplo
Estabilidad BIBO
Teorema del Valor Final
Si el sistema converge, ¿A qué converge?
Valor en estado estable o estacionario de \(y\)
Teorema del valor final
Si el sistema converge, ¿A qué converge?
El sistema debe ser asintóticamente estable.
Valor en estado estable o estacionario de \(y\)
¿Cuál es el valor en estado estable de la salida?
¿Cuál es el valor en estado estable de la salida?
G = tf(1, [1, 2])
step(G)
linearSystemAnalyzer(G)Ejercicio 1
¿Cuál es la salida en estado estable cuando \(u(t)=\mathbf{1}(t)\)?
Respuesta transitoria
Sistemas de primer orden
(asintóticamente) estable \(\Rightarrow\) único polo real en \(s=-\sigma\) con \(\sigma>0\)
constante de tiempo
La constante de tiempo es el único parámetro de rendimiento para sistemas de primer orden.
Un parámetro de rendimiento representa a alguna característica (en el tiempo) de la respuesta del sistema pero en función de cantidades en \(\mathcal{L}\).
Sistemas de segundo orden
forma estándar
se asume (asintóticamente) estable con polos en
forma estándar
\(\zeta\equiv\) factor o coeficiente de amortiguamiento
\(\to\) sub-amortiguado: \(\quad 0<\zeta<1\)
\(\to\) críticamente amortiguado: \(\quad \zeta=1\)
\(\to\) sobre-amortiguado: \(\quad \zeta>1\)
forma estándar
\(\omega_n\equiv\) frecuencia natural o frecuencia sin amortiguamiento
\(\sigma=\zeta\omega_n\)
\(\omega_d=\omega_n\sqrt{1-\zeta^2}\equiv\) frecuencia amortiguada
tiempo de subida
tiempo pico
% de overshoot o
sobreoscilación / sobreelevación
\(\epsilon\sim\) 5%, 2%, 1%
tiempo de asentamiento o establecimiento
\(t_r, t_s\) y \(M_p\) como parámetros de rendimiento para sistemas de segundo orden
S = stepinfo(sys)
S = stepinfo(y, t, yfinal)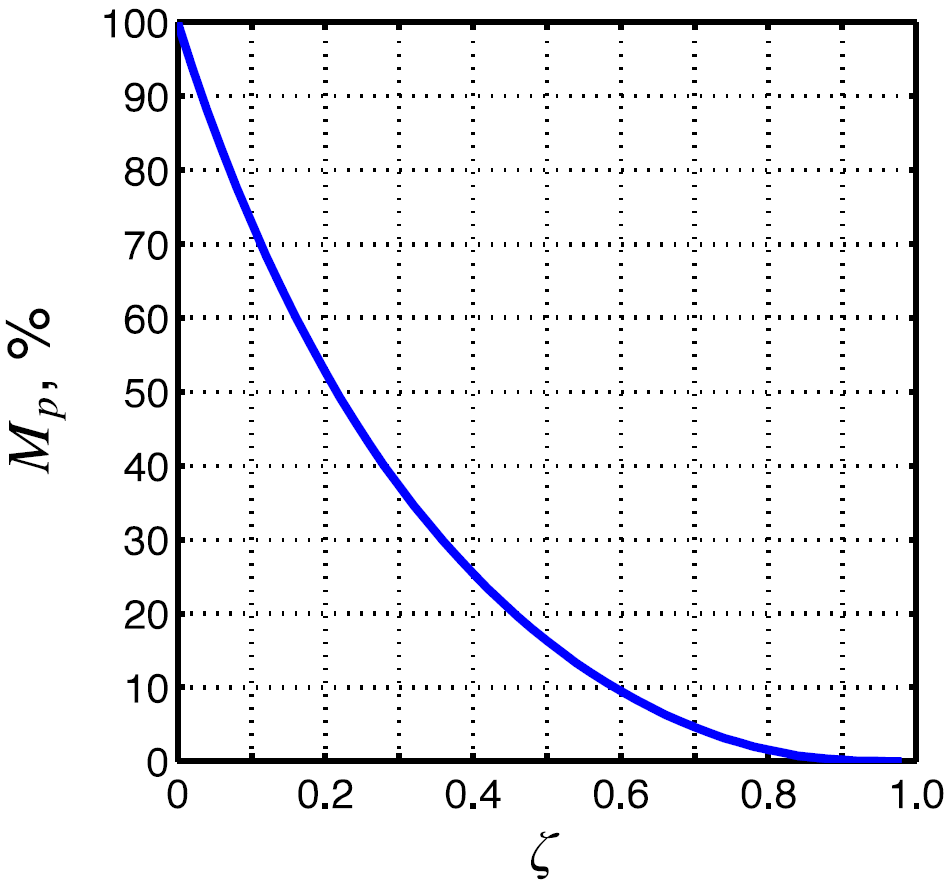
¿Cuál es la función de transferencia de un sistema que presente un \(t_r\approx0.5 \text{ s}\) y un \(M_p\approx10\%\)?
wn = 3.6;
zeta = 0.6;
G = tf(wn^2, [1, 2*zeta*wn, wn^2])¿Cuál es la función de transferencia de un sistema que presente un \(t_r\approx0.5 \text{ s}\) y un \(M_p\approx10\%\)?
¿Qué pasa cuando los sistemas tienen ceros o son de orden superior?
- \(+1\) polo en el LHP incrementa el \(t_r\) si se encuentra dentro de un factor de \(\approx 4\) de la parte real de los polos dominantes.
- \(+1\) cero en el LHP incrementa el \(M_p\) si se encuentra dentro de un factor de \(\approx 4\) de la parte real de los polos dominantes.
- \(+1\) cero en el RHP disminuye el \(M_p\) pero puede causar que la respuesta inicie en la dirección incorrecta \(\Rightarrow\) delay.
>> clase6_aproximaciones2dorden.m
\(\approx\) sistema de 1er orden
lejos de \(\jmath\omega\)
polos insignificantes
cerca de \(\jmath\omega\)
polos dominantes
\(\approx\) sistema de 2do orden
delay