
BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
Lección 7: El controlador PID
¿En dónde estamos por el momento?
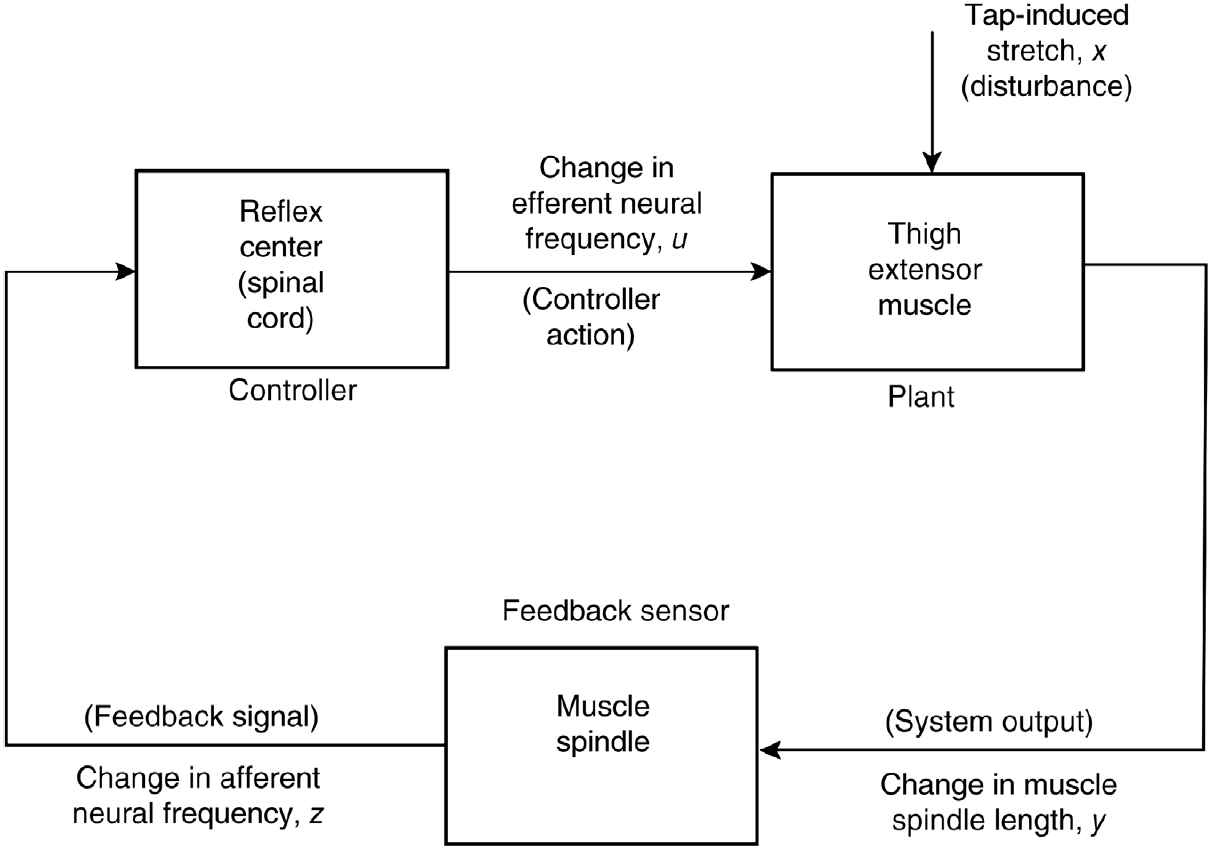
referencia
planta
sensor
controlador
salida
retroalimentación negativa
Nos hemos enfocado en el modelado y análisis de la planta
Objetivo principal del sistema de control: forzar que la planta se comporte de una manera deseada.
¿Qué hace el controlador? ¿Qué es el control en sí?
El controlador PID
error
¿Cuál es la idea?
proporcional = presente
integral = pasado
derivativo = futuro
derivativo = futuro
¿Por qué funciona esto?
Control PID de un sistema de 2do orden
¿Dónde se encuentran los polos del equivalente en lazo abierto?
Los polos corresponden a las soluciones de la ecuación característica:
función de transferencia del sistema en lazo abierto
Los polos corresponden a las soluciones de la ecuación característica:
función de transferencia del sistema en lazo abierto
3 soluciones \(\Rightarrow\) 3 polos + 3 ctes. PID = sistema de 3 ecuaciones con 3 incógnitas con solución donde queramos (en teoría)
Todo sistema \(\approx\) sistema 2do orden
PID controla sistemas de 2do orden
\(\approx\) PID controla todo sistema
Puede ajustarse de manera heurística
\(\approx\) suficientemente buena, más no óptima ni perfecta.
No necesariamente requiere de un modelo de la planta para ajustarse.
Reglas o "rules of thumb" prácticas.
Ventajas prácticas del control PID
Diseño sin modelo
(debe tenerse acceso a la respuesta al escalón)
parámetro
\(M_p\) y oscilaciones
estabilidad
cambio
pequeño
cambio
pequeño
elimina
no tiene efecto (en teoría)
degrada
degrada
mejora
Típicamente se inicia* con las constantes en cero, luego se incrementa \(k_P\) hasta tener un sistema estable y luego se usa la tabla.
Al disminuir las constantes se obtiene el efecto opuesto de la tabla (supuestamente).
* pueden encontrarse las constantes iniciales con métodos como el de Ziegler-Nichols (lectura adicional).
Ejemplo: servomotor

potenciómetro
voltaje a ángulo
motor + carga + caja
ángulo de referencia
posición angular del eje
>> clase7_servomotor.m
Ejemplo: servomotor

potenciómetro
voltaje a ángulo
motor + carga + caja
ángulo de referencia
posición angular del eje
>> clase7_servomotor.m
Requerimientos:
- \(e_{ss}=0\)
- \(t_r\le 5\) s
- \(t_s\le 30\) s
- \(M_p\le 25\%\)
Ejemplo: avión de ataque
IMU
alerones + dinámica del avión
ángulo de banqueo deseado
ángulo de banqueo
>> clase7_avion.m
Ejemplo: avión de ataque
IMU
alerones + dinámica del avión
ángulo de banqueo deseado
ángulo de banqueo

>> clase7_avion.m
Requerimientos:
- estabilizar
- \(e_{ss}=0\)
- \(M_p\le 25\%\)
- respuesta rápida
Ejemplo: generador eólico
velocidad deseada
velocidad del generador
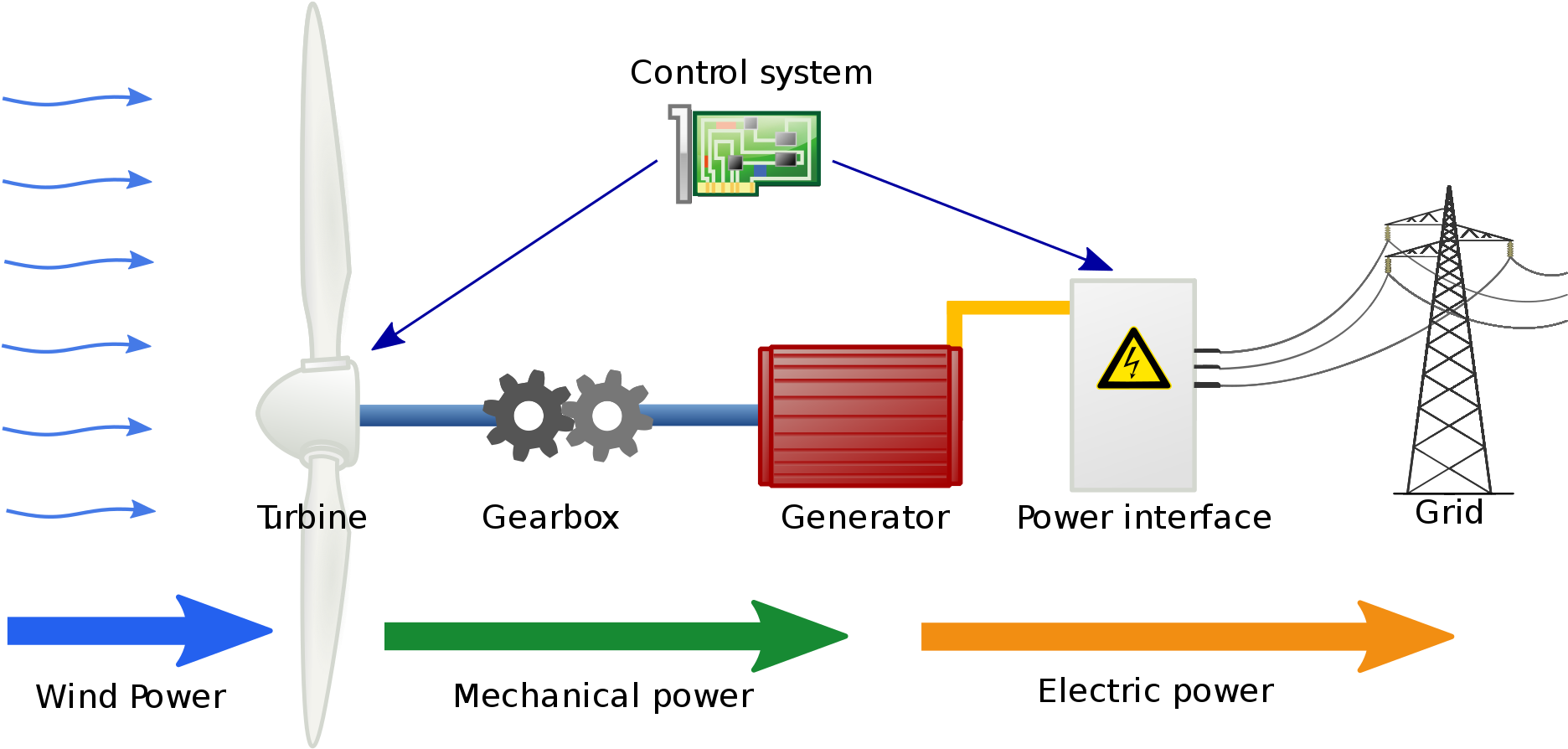
>> clase7_generador.m
Ejemplo: generador eólico
velocidad deseada
velocidad del generador

>> clase7_generador.m
Requerimientos:
- sólo control PI
- \(e_{ss}=0\)
- \(t_r\le 1\) s
Diseño con modelo
Podemos usar herramientas como el PID Tuner de MATLAB para diseñar el controlador, según las especificaciones o requerimientos.
>> clase7_pid_tuner.m
Implementación
Implementación analógica
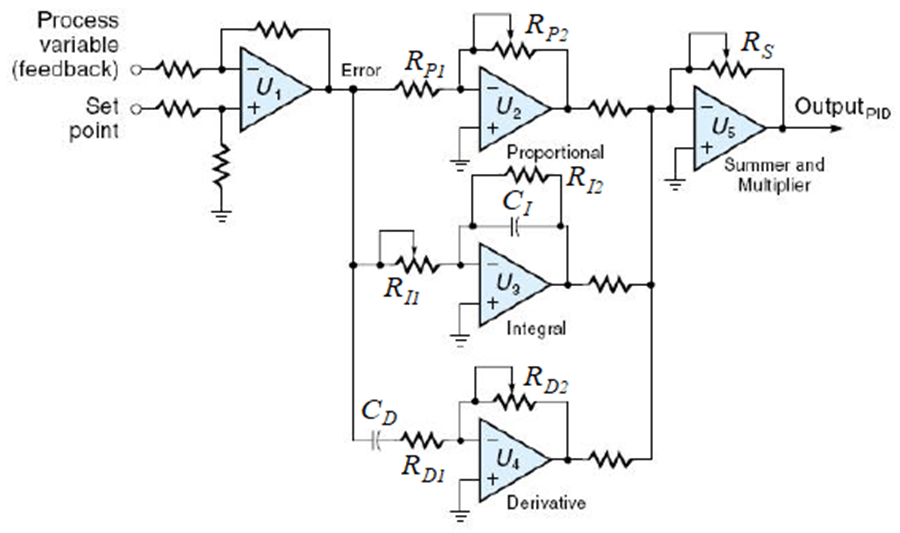
Implementación digital
Implementación digital
Implementación digital
Implementación digital
error acumulado
Implementación digital
De lo cual obtenemos la versión digital del controlador PID:
// Inicialización
e_k_1 = 0, E_k_1 = 0;
kP, kI_ast, kD_ast; // ya incluyen el período de muestreo
loop()
{
r_k = leer_referencia(); // puede ser una cte. definida
y_k = leer_sensor();
// PID
e_k = r_k - y_k;
E_k = E_k_1 + e_k;
eD = e_k - e_k_1;
u_k = kP*e_k + kI_ast*E_k + kD_ast*eD;
// u_k = kP*e_k + (kI*dt)*E_k + (kD/dt)*eD; // si no incluyen el Ts
mandar_a_actuador(u_k);
e_k_1 = e_k;
E_k_1 = E_k;
}