Lección 9: De la Función de Transferencia al Espacio de Estados

BE3024 - Sistemas de Control 1 (Biomédica)
2do ciclo, 2024
¿Dónde se ha quedado corta nuestra perspectiva actual de control?
Múltiples entradas y salidas
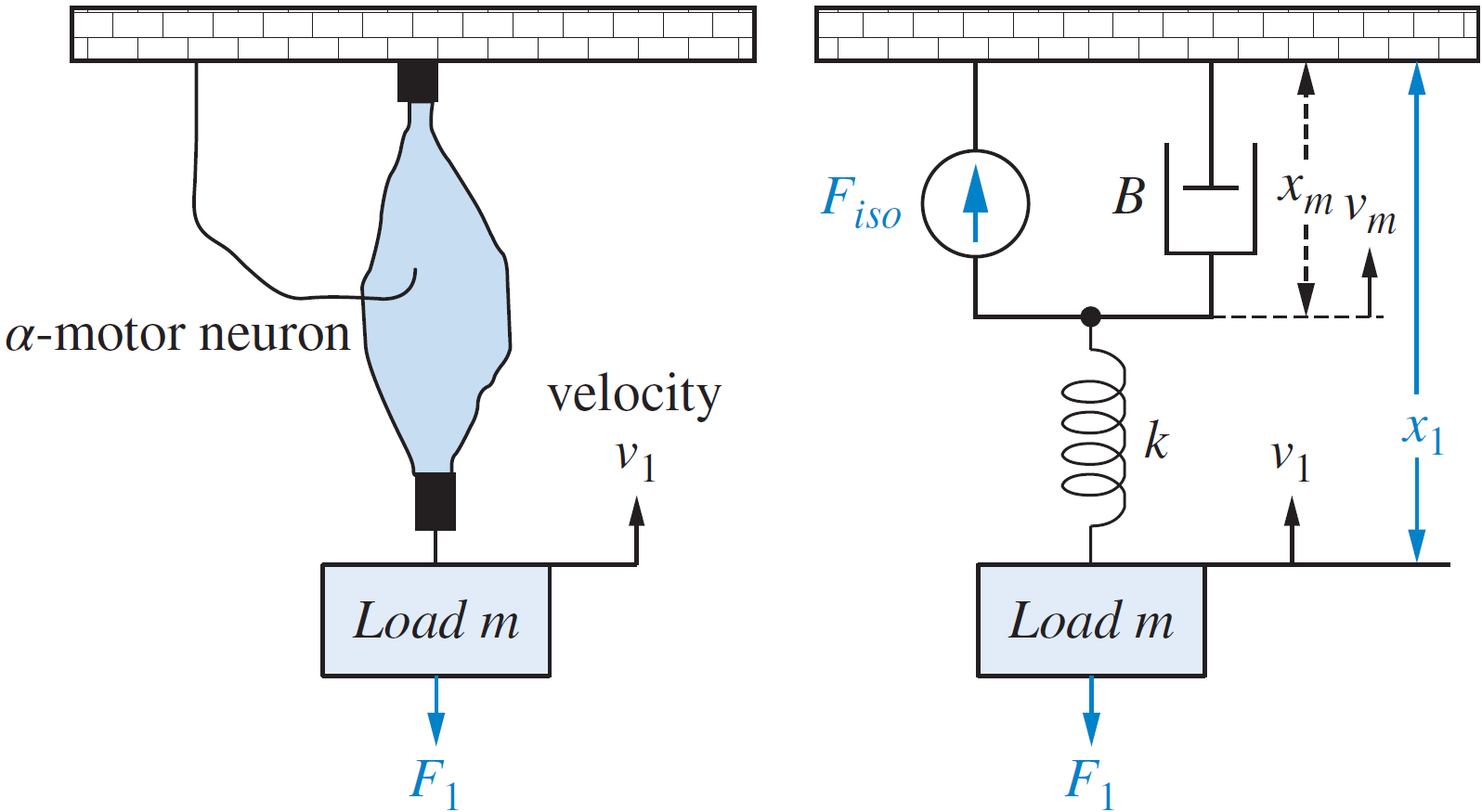
pero fue necesario hacer \(F_{iso}=0\)
pero fue necesario hacer \(F_1=0\)
pero fue necesario hacer \(F_{iso}=0\)
pero fue necesario hacer \(F_1=0\)
¿Y si queremos considerar ambas fuerzas? ¿O quisiéramos analizar qué pasa con \(x_1\) tanto como con \(x_2\)?
Problema: la perspectiva clásica sólo permite una entrada y una salida.
Información oculta
modelo mínimo de Bergman
glucemia
tasa de ingreso de insulina
ingesta de glucosa
Información oculta
modelo mínimo de Bergman
glucemia
tasa de ingreso de insulina
ingesta de glucosa
glucemia
tasa de ingreso de insulina
ingesta de glucosa
¿Y el resto de información?
glucemia
tasa de ingreso de insulina
ingesta de glucosa
¿Y el resto de información?
Problema: al plantear modelos entrada-salida, la perspectiva clásica se pierde de información interna del sistema.
Condiciones iniciales
modelo mínimo de Bergman
glucemia
tasa de ingreso de insulina
ingesta de glucosa
Con condiciones iniciales iguales a cero.
Con condiciones iniciales iguales a cero.
¡El paciente está muerto!
con condiciones iniciales iguales a cero
el paciente está muerto!
Problema: la perspectiva clásica no puede (o tiene una forma extraña de) lidiar con condiciones iniciales distintas a cero.
La abstracción de \(\mathcal{L}\)
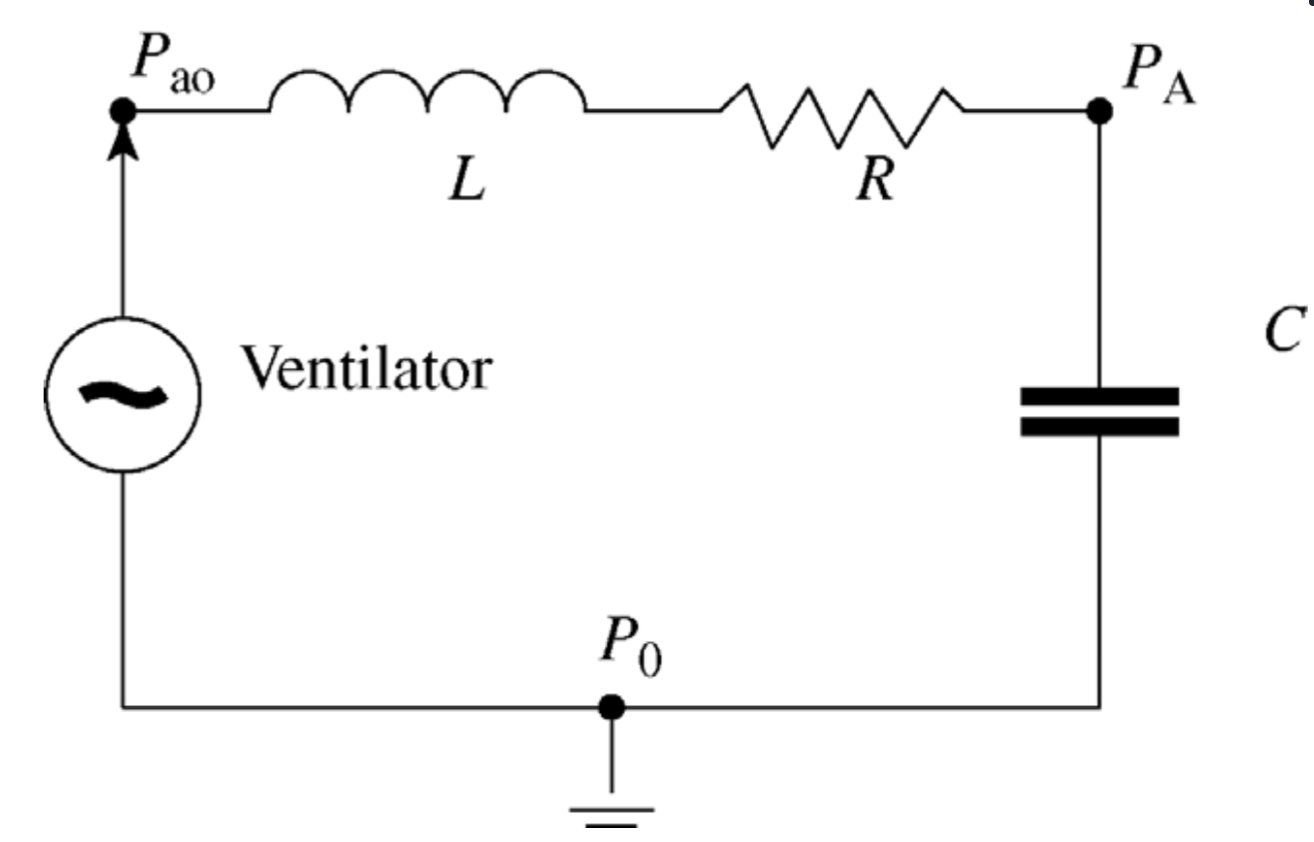
Para diseñar esquema de ventilación \(C_1(s)\) para paciente con neumonía severa.

El paciente presentó una mejoría significativa.

Sin embargo, luego de unos días, el esquema \(C_1(s)\) le causa hiperoxia.
El paciente presentó una mejoría significativa.

¿Qué pasó?
\(C_1(s)\) debería haber cambiado cuando el paciente pasó de \(G_1(s)\) a \(G_2(s)\).
El paciente presentó una mejoría significativa.
Sin embargo, luego de unos días, el esquema \(C_1(s)\) le causa hiperoxia.
Laplace se "come" al dominio de tiempo
Laplace se "come" al dominio de tiempo
Problema: la transformada de Laplace asume que los sistemas presentan un mismo comportamiento desde el inicio hasta el final del universo en términos de tiempo.
¿Cómo resolvemos estos problemas?
G = tf(-0.017892, [1, 0.2956, 0.00399588, 0]);
sys = ss(G)G = tf(-0.017892, [1, 0.2956, 0.00399588, 0]);
sys = ss(G)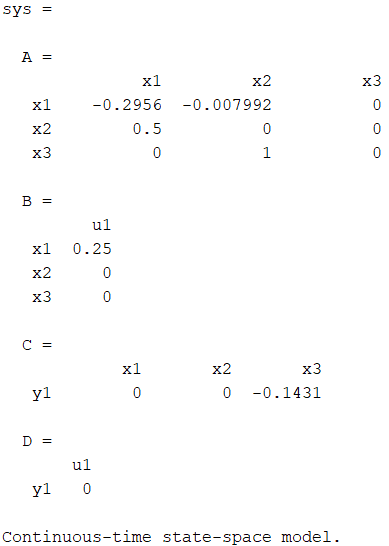
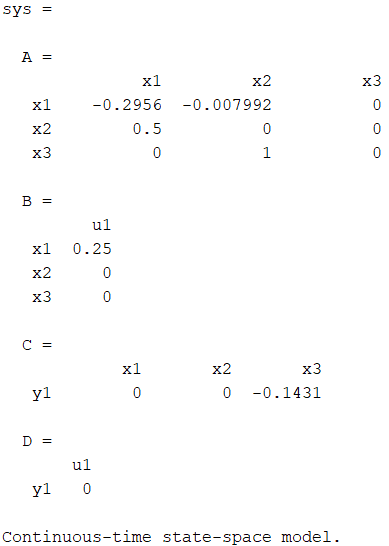
G = tf(-0.017892, [1, 0.2956, 0.00399588, 0]);
sys = ss(G)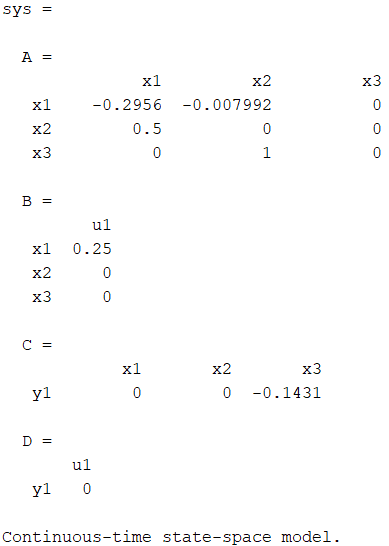
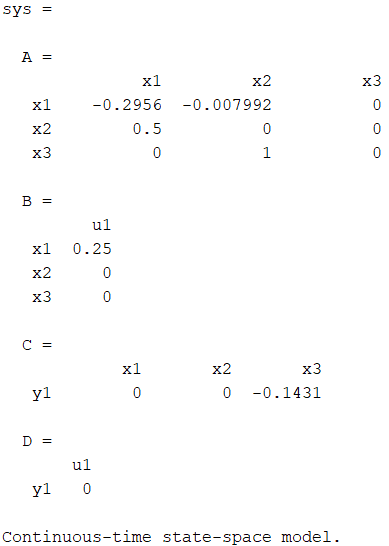
¿Qué es esto?
Es el mismo sistema pero en una representación distinta.
Representación en el Espacio de Estados
vector de entradas
vector de salidas
vector de estado
variables de estado
matrices del sistema
El estado de un sistema es una colección de variables (de estado) o cantidades físicas que caracteriza completamente (en la ausencia de excitaciones externas) su comportamiento actual y puede usarse para predecir su comportamiento futuro.
¿Ventajas de esta representación?
- Multivariable
- Perspectiva completa
- Condiciones iniciales arbitrarias
- Permite sistemas que varían en el tiempo
- Permite sistemas no lineales
- Se presta mejor a métodos computacionales
Repaso de conceptos matemáticos necesarios
Vectores
Un vector \(\mathbf{v}\) es una lista ordenada de números reales (escalares) \(v_1,v_2,...,v_n\) apilados verticalmente de la forma: $$\qquad$$ $$\mathbf{v}=\begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}=\begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix}^\top \in\mathbb{R}^n$$ $$\qquad$$
Puede emplearse la transpuesta para obtener un vector fila a partir de un vector columna.
Gráficamente, puede representarse a un vector como una flecha dirigida desde el origen hasta el punto situado en las coordenadas dadas por los elementos del vector.
Sin embargo, puede considerarse también al vector como el punto mismo dentro de algún espacio \(n\)-dimensional.

Escalamiento
Se reparte el escalar, \(\alpha\in\mathbb{R}\), elemento por elemento.
Si \(\alpha>0\) entonces la operación sólo cambia el tamaño del vector, mientras que si \(\alpha<0\) también le cambia el sentido.

Suma y resta
Se realiza elemento por elemento, sólo está definida entre vectores de la misma dimensión.
Claramente \(\mathbf{v}+\mathbf{w}\) no está definido, sin embargo

Producto interno
El producto interno entre dos vectores de la misma dimensión se define como la suma de los productos, elemento por elemento, de dos vectores \(\mathbf{v}, \mathbf{w} \in \mathbb{R}^n\).
Norma
El producto interno de un vector consigo mismo brinda una noción de magnitud denominada norma.
La más común es la norma Euclideana, la cual corresponde a la longitud del vector y se denota como:
Existen otras normas además de la Euclideana.
Se emplea el sub-índice para diferenciarlas entre sí.
Norma del valor absoluto (o Manhattan):
Norma infinito (o del supremo):
Propiedades del producto interno
\(\mathbf{v} \cdot \mathbf{w}=\mathbf{w} \cdot \mathbf{v}\)
\(\mathbf{v} \cdot (\alpha\mathbf{w})=\alpha(\mathbf{v} \cdot \mathbf{w})\)
\(\mathbf{u} \cdot (\mathbf{v}+\mathbf{w})=\mathbf{u} \cdot \mathbf{v}+\mathbf{u} \cdot \mathbf{w}\)
\( \|\mathbf{v} + \mathbf{w}\|^2 = \|\mathbf{v}\|^2+2(\mathbf{v}\cdot\mathbf{w})+\|\mathbf{w}\|^2\)
\( \|\mathbf{v} + \mathbf{w}\|\le \|\mathbf{v}\|+\|\mathbf{w}\|\) (desigualdad triangular)
\(\mathbf{v} \cdot \mathbf{w}=\|\mathbf{v}\|\|\mathbf{w}\|\cos\theta\)

Ortogonalidad
Si \(\mathbf{v}\in\mathbb{R}^n\) presenta \(\|\mathbf{v}\|=1\) entonces se conoce como vector unitario y puede denotarse como \(\hat{\mathbf{v}}\).
Puede obtenerse un vector unitario a partir de cualquier vector mediante la normalización \(\hat{\mathbf{w}}=\mathbf{w}/\|\mathbf{w}\|\).
Si el producto interno entre dos vectores es cero, entonces se dice que estos son ortogonales (si y sólo si).
Si, adicionalmente, dos vectores ortogonales tienen norma unitaria se dice que estos son ortonormales.

ortogonales más no ortonormales
ortonormales
Matrices
El segundo objeto de interés en el algebra lineal corresponde a las matrices, las cuales pueden considerarse como una generalización para los vectores.
Se define una matriz como un arreglo rectangular de elementos con \(m\) filas y \(n\) columnas.
Para cada elemento: \(a_{ij}\in\mathbb{R}\).
Si \(m=n\) se dice que la matriz es cuadrada.
Si ya sea \(n=1\) o \(m=1\) entonces se obtiene un vector columna o fila respectivamente.
Las operaciones de suma, resta y escalamiento funcionan igual para matrices que con vectores.
La operación de transposición intercambia las filas con las columnas de la matriz. Si \(\mathbf{A}\in\mathbb{R}^{m \times n}\) entonces \(\mathbf{A}^\top\in\mathbb{R}^{n \times m}\) y recibe el nombre de la transpuesta de \(\mathbf{A}\).
Multiplicación de matrices
Es una operación poco intuitiva ya que tiene que tomar en consideración la diversidad de dimensiones de las matrices.
Entonces se define la multiplicación \(\mathbf{A}\mathbf{B}\) entre matrices como
es decir, se efectúa el producto interno de cada fila de \(\mathbf{A}\) con cada columna de \(\mathbf{B}\).
Por lo tanto, para que la multiplicación entre matrices esté definida, el número de columnas de \(\mathbf{A}\) debe ser igual al número de filas de \(\mathbf{B}\).
De esto se concluye que la multiplicación entre matrices no es conmutativa.
Por ejemplo, si se tienen las matrices
claramente \(\mathbf{C}\mathbf{D}\) no está definida, sin embargo

Inversa de una matriz
Operación análoga a la división para escalares, bajo la definición de un recíproco o inverso multiplicativo.
Cumple con la relación
donde \(\mathbf{A}^{-1}\) se denomina la inversa de \(\mathbf{A}\).
Dado que la multiplicación por la inversa es conmutativa, se concluye que esta existe sólo para matrices cuadradas.
Sin embargo, no toda matriz cuadrada posee inversa y se refiere a ellas como singulares.
En general, los procedimientos analíticos para encontrar la inversa de una matriz son tediosos y complicados, especialmente para matrices de dimensiones superiores. Por esta razón, a menos que se trate de una matriz de \(2 \times 2\), se acudirá frecuentemente a métodos numéricos para determinarla.
Para una matriz de \(2 \times 2\) puede emplearse la fórmula:
Matrices cuadradas de importancia
Matriz cero
Matrices diagonales
Matriz identidad (el "uno" matricial)
Matrices simétricas
Matrices antisimétricas
Matrices triangulares superiores
Matrices ortogonales
Matrices triangulares inferiores
Determinante
Permite obtener un escalar a partir de una matriz cuadrada.
Se emplea en la solucion de sistemas de ecuaciones lineales, para definir una fórmula general para invertir matrices y para determinar el factor de escalamiento de una transformación lineal.
No existe una fórmula general para el determinante ya que la complejidad de determinar el mismo depende de la dimensión de la matriz.
Sin embargo, existen las siguientes fórmulas:
Algunas identidades
\(\mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}\)
\(\mathbf{A}\mathbf{B}\ne \mathbf{B}\mathbf{A}\)
\(\mathbf{A}+(\mathbf{B}+\mathbf{C})=(\mathbf{A}+\mathbf{B})+\mathbf{C}\)
\(\mathbf{A}(\mathbf{B}\mathbf{C})=(\mathbf{A}\mathbf{B})\mathbf{C}\)
\((\mathbf{A}+\mathbf{B})^\top=\mathbf{A}^\top+\mathbf{B}^\top\)
\((\mathbf{A}\mathbf{B})^\top=\mathbf{B}^\top\mathbf{A}^\top\)
\((\mathbf{A}+\mathbf{B})^{-1}\ne \mathbf{A}^{-1}+\mathbf{B}^{-1}\)
\((\mathbf{A}\mathbf{B})^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1}\)
\(\left(\mathbf{A}^{-1}\right)^{-1}=\mathbf{A}\)
\(\mathrm{det}(\mathbf{A}\mathbf{B})=\mathrm{det}(\mathbf{A})\mathrm{det}(\mathbf{B})\)
\(\mathrm{det}\left(\mathbf{A}^\top\right)=\mathrm{det}(\mathbf{A})\)
\(\mathrm{det}\left(\mathbf{A}^{-1}\right)=1/\mathrm{det}(\mathbf{A})\)
Eigenvalores y eigenvectores
Si se tiene una matriz \(\mathbf{A}\in\mathbb{R}^{n\times n}\) entonces su polinomio característico está dado por:
Los eigenvalores de \(\mathbf{A}\) son las soluciones de la ecuación característica:
son por lo general complejos y \(\mathbf{A}\) (en este caso) siempre tendrá \(n\) eigenvalores (puede que algunos se repitan).
Se llama espectro de \(\mathbf{A}\) al conjunto formado por todos los eigenvalores de \(\mathbf{A}\) y se denota como
Los eigenvalores resuelven el problema de eigenvalores en álgebra lineal:
donde \(\mathbf{v}_i\in\mathbb{R}^n\) se conocen como eigenvectores y hay uno asociado a cada eigenvalor de \(\mathbf{A}\). En otras palabras, los eigenvectores son aquellos a los cuales la aplicación de la matriz \(\mathbf{A}\) es equivalente a un escalamiento de magnitud igual a los eigenvalores.
Cálculo vectorial y matricial
Sea \(\mathbf{x}\in \mathbb{R}^n\). Una función escalar multivariable está definida como \(f:\mathbb{R}^n \to \mathbb{R}\) tal que
donde \(x_i\) corresponde a los elementos de \(\mathbf{x}\). Se define el gradiente de la función escalar como el vector columna dado por:
Un campo vectorial (o función vectorial) está definido como
\(\mathbf{f}:\mathbb{R}^n \to \mathbb{R}^m\) tal que
en donde \(f_1,f_2,...,f_m\) son funciones escalares multivariable.
Se define el jacobiano del campo vectorial como la matriz tal que
El jacobiano es, efectivamente, la derivada del campo vectorial.
Si \(\mathbf{A}(t)\) es una matriz que depende del tiempo tal que
entonces, se definen