Repaso de álgebra lineal

BE3027 - Robótica Médica
el alto grado de movilidad que presenta la gran mayoría de robots hace prácticamente imposible resolver analíticamente problemas de aplicación no triviales
¿Por qué
¿Por qué
debe recurrirse frecuentemente a métodos numéricos que implican múltiples operaciones entre matrices y vectores, por ende, álgebra lineal
el álgebra lineal también estudia a los espacios vectoriales y las transformaciones lineales que pueden realizarse sobre ellos, lo cual brindará una notación estándar de importancia en robótica
¿Por qué
Vectores y espacios vectoriales
un vector \(\mathbf{v}\) es una lista ordenada de números reales (escalares) \(v_1,v_2,...,v_n\) apilados verticalmente de la forma:
puede emplearse la transpuesta para obtener un vector fila a partir de un vector columna.
gráficamente, puede representarse a un vector como una flecha dirigida desde el origen hasta el punto situado en las coordenadas dadas por los elementos del vector

gráficamente, puede representarse a un vector como una flecha dirigida desde el origen hasta el punto situado en las coordenadas dadas por los elementos del vector

sin embargo, puede considerarse también al vector como un objeto (el punto mismo) dentro de algún espacio \(n\)-dimensional
se reparte el escalar, \(\alpha\in\mathbb{R}\), elemento por elemento

Escalamiento
se reparte el escalar, \(\alpha\in\mathbb{R}\), elemento por elemento

Escalamiento
si \(\alpha>0\) entonces la operación sólo cambia el tamaño del vector, mientras que si \(\alpha<0\) también le cambia el sentido
elemento por elemento, sólo está definida entre vectores de la misma dimensión
Suma y resta
claramente \(\mathbf{v}+\mathbf{w}\) no está definido, sin embargo

se define como la suma de los productos, elemento por elemento, de dos vectores \(\mathbf{v}, \mathbf{w} \in \mathbb{R}^n\) de la misma dimensión
Producto interno
el producto interno de un vector consigo mismo brinda una noción de magnitud denominada norma, la más común es la norma Euclideana (longitud del vector) y se denota como
Norma
existen otras normas además de la Euclideana y se emplea el sub-índice para diferenciarlas entre sí
norma del valor absoluto:
norma uniforme (o del supremo):
\(\mathbf{v} \cdot \mathbf{w}=\mathbf{w} \cdot \mathbf{v}\)
\(\mathbf{v} \cdot (\alpha\mathbf{w})=\alpha(\mathbf{v} \cdot \mathbf{w})\)
\(\mathbf{u} \cdot (\mathbf{v}+\mathbf{w})=\mathbf{u} \cdot \mathbf{v}+\mathbf{u} \cdot \mathbf{w}\)
\( \|\mathbf{v} + \mathbf{w}\|^2 = \|\mathbf{v}\|^2+2(\mathbf{v}\cdot\mathbf{w})+\|\mathbf{w}\|^2\)
\( \|\mathbf{v} + \mathbf{w}\|\le \|\mathbf{v}\|+\|\mathbf{w}\|\)
\(\mathbf{v} \cdot \mathbf{w}=\|\mathbf{v}\|\|\mathbf{w}\|\cos\theta\)

Propiedades del producto interno
si \(\mathbf{v}\in\mathbb{R}^n\) presenta \(\|\mathbf{v}\|=1\) entonces se conoce como vector unitario y puede denotarse como \(\hat{\mathbf{v}}\)
puede obtenerse un vector unitario a partir de cualquier vector mediante la normalización \(\hat{\mathbf{w}}=\mathbf{w}/\|\mathbf{w}\|\)
Ortogonalidad
si el producto interno entre dos vectores es cero, entonces se dice que estos son ortogonales
si, adicionalmente, dos vectores ortogonales tienen norma unitaria se dice que estos son ortonormales
Ortogonalidad

ortogonales más no ortonormales
ortonormales

el resultado es un vector que es ortogonal a los vectores empleados para generarlo, esta operación se encuentra definida exclusivamente para vectores en \(\mathbb{R}^3\) de la forma
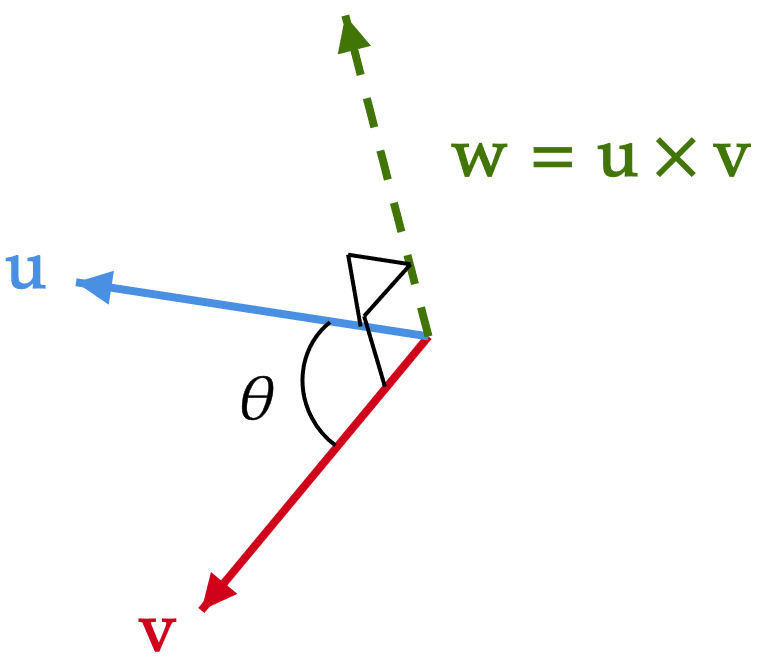
Producto cruz
por ejemplo:
en donde puede verse que:
las operaciones de suma y escalamiento toman uno o mas vectores en \(\mathbb{R}^n\) y retornan otro vector en \(\mathbb{R}^n\), el concepto abstracto detrás de esto nos permite defnir una estructura llamada grupo, el cual requiere un conjunto de objetos \(\mathcal{G}\) y una operación entre ellos \(\cdot\) que cumplan con los llamados axiomas de grupo
Grupos
clausura
para todo \(a,b \in \mathcal{G}\), el resultado de la operación \(a \cdot b\) también se encuentra dentro de \(\mathcal{G}\)
asociatividad
para todo \(a, b, c \in \mathcal{G}\) se cumple que \((a \cdot b)\cdot c=a \cdot (b \cdot c)\)
Grupos
identidad
existe un unico elemento \(e \in \mathcal{G}\) tal que \(a \cdot e=e \cdot a=a\)
inversa
para cada \(a \in \mathcal{G}\) existe un elemento \(b \in \mathcal{G}\), denotado
\(b = a^{-1}\) (o \(b = -a\) si se emplea la suma), tal que
\(a \cdot b=b \cdot a = e\)
Grupos
toma lo observado con vectores, su adición y su escalamiento para refinar la definición de grupo
se define un espacio vectorial (sobre los reales) como un conjunto \(\mathcal{V}\) para el cual se definen dos operaciones, la multiplicación por un escalar y la suma de vectores, que cumplan con las siguientes 10 propiedades
Espacios vectoriales
1. \(\mathbf{x} + \mathbf{y} \in \mathcal{V}\) para todo \(\mathbf{x}, \mathbf{y} \in \mathcal{V}\).
2. \(\mathbf{x} + \mathbf{y} = \mathbf{y} + \mathbf{x}\) para todo \(\mathbf{x}, \mathbf{y} \in \mathcal{V}\).
3. \((\mathbf{x} + \mathbf{y}) + \mathbf{z} = \mathbf{x} + (\mathbf{y} + \mathbf{z})\) para todo \(\mathbf{x}, \mathbf{y}, \mathbf{z} \in \mathcal{V}\).
4. Existe un elemento \(\mathbf{0} \in \mathcal{V}\) tal que \(\mathbf{x} + \mathbf{0} = \mathbf{x}\) para todo \(\mathbf{x} \in \mathcal{V}\).
5. Para cada \(\mathbf{x} \in \mathcal{V}\), existe un elemento \(-\mathbf{x} \in \mathcal{V}\) tal que \(\mathbf{x} + (-\mathbf{x}) = \mathbf{0}\).
6. \(\alpha\mathbf{x} \in \mathcal{V}\) para todo \(\alpha \in \mathbb{R}\) y todo \(\mathbf{x} \in \mathcal{V}\).
7. \((\alpha\beta)\mathbf{x}=\alpha(\beta\mathbf{x})\) para todo \(\alpha,\beta \in \mathbb{R}\) y todo \(\mathbf{x} \in \mathcal{V}\).
8. \((\alpha+\beta)\mathbf{x}=\alpha\mathbf{x}+\beta\mathbf{x}\) para todo \(\alpha,\beta \in \mathbb{R}\) y todo \(\mathbf{x} \in \mathcal{V}\).
9. \(\alpha(\mathbf{x}+\mathbf{y})=\alpha\mathbf{x}+\alpha\mathbf{y}\) para todo \(\alpha \in \mathbb{R}\) y todo \(\mathbf{x},\mathbf{y} \in \mathcal{V}\).
10. \(1\mathbf{x}=\mathbf{x}\) para todo \(\mathbf{x}\in\mathcal{V}\).
nótese que el conjunto de vectores en \(\mathbb{R}^n\) corresponde, junto con la suma vectorial y el escalamiento, a un espacio vectorial canónico
se denomina subespacio (ya que también es un espacio vectorial) a un subconjunto de un espacio vectorial más grande
un conjunto de vectores \(\mathbf{x}_1,...,\mathbf{x}_k\) es linealmente independiente si (\(\alpha_j\in\mathbb{R}\))
Independencia lineal
NOTA: \(\mathbf{x}_1,...,\mathbf{x}_k\) NO pueden ser el vector cero \(\mathbf{0}\)
dado un conjunto de vectores \(\{\mathbf{x}_1,...,\mathbf{x}_k\}\) en \(\mathbb{R}^n\), el conjunto generador o span de los vectores, denotado como \(\mathrm{span}\{\mathbf{x}_1,...,\mathbf{x}_k\}\), es el set de vectores \(\mathbf{y}\) en \(\mathbb{R}^n\) tal que
Conjunto generador
para \(\alpha_1,...,\alpha_k\) escalares
en general es un subespacio de \(\mathbb{R}^n\), con dimensión \(\mathrm{dim}(\mathcal{V})\) igual al número de vectores linealmente independientes dentro del conjunto de vectores
sólo es igual a \(\mathbb{R}^n\) cuando \(k=n\) y todos los vectores son linealmente independientes, en cuyo caso los vectores conforman una base para \(\mathbb{R}^n\)
dentro de un espacio vectorial, es posible expresar vectores mediante una combinación lineal de otros vectores
por ejemplo, el vector \(\begin{bmatrix} x & y \end{bmatrix}^\top\in\mathbb{R}^2\) puede representarse como:
Bases
en donde \(\mathbf{e}_1,\mathbf{e}_2\) son los vectores de base
nos referimos al conjunto \(\{\mathbf{e}_1,\mathbf{e}_2\}\) como una base para \(\mathbb{R}^2\) ya que al variar los escalares \(x, y\) en la combinación lineal puede generarse todo vector contenido dentro de \(\mathbb{R}^2\)
en este caso particular, los vectores \(\mathbf{e}_1, \mathbf{e}_2\) forman una base ortonormal
Matrices y transformaciones lineales
se define una matriz como un arreglo rectangular de elementos con \(m\) filas y \(n\) columnas, estas pueden considerarse como una generalización para los vectores
para cada elemento: \(a_{ij}\in\mathbb{R}\)
si \(m=n\) se dice que la matriz es cuadrada
si ya sea \(n=1\) o \(m=1\) entonces se obtiene un vector columna o fila respectivamente
las operaciones de suma, resta y escalamiento funcionan igual para matrices que con vectores
la operación de transposición intercambia las filas con las columnas de la matriz
si \(\mathbf{A}\in\mathbb{R}^{m \times n}\) entonces \(\mathbf{A}^\top\in\mathbb{R}^{n \times m}\) y recibe el nombre de la transpuesta de \(\mathbf{A}\)
Multiplicación de matrices
se define la multiplicación \(\mathbf{A}\mathbf{B}\) entre matrices como
es decir, se efectúa el producto interno de cada fila de \(\mathbf{A}\) con cada columna de \(\mathbf{B}\)
por lo tanto, para que la multiplicación entre matrices esté definida, el número de columnas de \(\mathbf{A}\) debe ser igual al número de filas de \(\mathbf{B}\)
de esto se concluye que la multiplicación entre matrices no es conmutativa
por ejemplo, si se tienen las matrices

claramente \(\mathbf{C}\mathbf{D}\) no está definida, sin embargo
"división entre matrices" pero bajo la definición de un recíproco o inverso multiplicativo, que cumple con
Inversa
donde \(\mathbf{A}^{-1}\) se denomina la inversa de \(\mathbf{A}\)
dado que la multiplicación por la inversa es conmutativa, se concluye que esta existe sólo para matrices cuadradas
"división entre matrices" pero bajo la definición de un recíproco o inverso multiplicativo, que cumple con
Inversa
donde \(\mathbf{A}^{-1}\) se denomina la inversa de \(\mathbf{A}\)
sin embargo, no toda matriz cuadrada posee inversa y se refiere a ellas como singulares
en general, los procedimientos analíticos para encontrar la inversa de una matriz son tediosos y complicados, especialmente para matrices de dimensiones superiores
por esta razón, a menos que se trate de una matriz de \(2 \times 2\), se acudirá frecuentemente a métodos numéricos para determinarla
Matrices cuadradas de importancia
matriz cero
matriz identidad
matrices diagonales
matrices simétricas
matrices antisimétricas
matrices ortogonales
matrices triangulares superiores
matrices triangulares inferiores
permite obtener un escalar a partir de una matriz cuadrada
se emplea en la solucion de sistemas de ecuaciones lineales, para definir una fórmula general para invertir matrices y para determinar el factor de escalamiento de una transformación lineal
Determinante
no existe una fórmula general para el determinante ya que la complejidad de determinar el mismo depende de la dimensión de la matriz, sin embargo, existen las siguientes fórmulas
\(\mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}\).
\(\mathbf{A}\mathbf{B}\ne \mathbf{B}\mathbf{A}\).
\(\mathbf{A}+(\mathbf{B}+\mathbf{C})=(\mathbf{A}+\mathbf{B})+\mathbf{C}\).
\(\mathbf{A}(\mathbf{B}\mathbf{C})=(\mathbf{A}\mathbf{B})\mathbf{C}\).
\((\mathbf{A}+\mathbf{B})^\top=\mathbf{A}^\top+\mathbf{B}^\top\).
\((\mathbf{A}\mathbf{B})^\top=\mathbf{B}^\top\mathbf{A}^\top\).
Algunas identidades
\((\mathbf{A}+\mathbf{B})^{-1}\ne \mathbf{A}^{-1}+\mathbf{B}^{-1}\).
\((\mathbf{A}\mathbf{B})^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1}\).
\(\left(\mathbf{A}^{-1}\right)^{-1}=\mathbf{A}\).
\(\mathrm{det}(\mathbf{A}\mathbf{B})=\mathrm{det}(\mathbf{A})\mathrm{det}(\mathbf{B})\).
\(\mathrm{det}\left(\mathbf{A}^\top\right)=\mathrm{det}(\mathbf{A})\).
\(\mathrm{det}\left(\mathbf{A}^{-1}\right)=1/\mathrm{det}(\mathbf{A})\).
una transformación lineal es una función \(\mathcal{T}: \mathcal{V}_1 \to \mathcal{V}_2\), es decir, una función que toma elementos del espacio vectorial \(\mathcal{V}_1\) y los mapea a elementos del espacio vectorial \(\mathcal{V}_2\), que satisface:
Transformaciones lineales
para todos \(\alpha,\beta\in\mathbb{R}\) y \(\mathbf{v},\mathbf{w}\in\mathcal{V}_1\)
\(\mathcal{T}\{\mathbf{v}\}\) y \(\mathcal{T}\{\mathbf{w}\}\) son entonces elementos que pertenecen al espacio vectorial \(\mathcal{V}_2\)
algunos ejemplos
escalamiento
proyección
reflección
una observación importante sobre las transformaciones lineales es que si se representa un vector (que pertenece a un espacio vectorial) mediante una base para el mismo, por ejemplo \(\mathbb{R}^n\)
es posible emplear la definición para determinar que
\(\mathcal{T}\{\mathbf{e}_1\},\mathcal{T}\{\mathbf{e}_2\},...,\mathcal{T}\{\mathbf{e}_n\}\) son vectores (columna) que pertenecen a otro espacio vectorial
por lo tanto, puede definirse una matriz \(\mathbf{T}\) tal que
por lo que se llega a la conclusión que
es decir, una transformacion lineal \(\mathcal{T}\) siempre tendrá asociada una matriz \(\mathbf{T}\) y la aplicación de la primera es equivalente a una multiplicación matriz-vector con la segunda
de manera sencilla, las transformaciones lineales son matrices
por ejemplo, si se tiene la siguiente transformación lineal
y se representa al vector \(\begin{bmatrix} x & y \end{bmatrix}^\top\) mediante la base canónica de \(\mathbb{R}^2\), es decir, si
entonces
lo cual es equivalente a
sabiendo que las transformaciones lineales tienen matrices asociadas es sencillo definir la composición entre ellas mediante multiplicación de matrices
adicionalmente, se denomina rígida a toda transformación lineal (puede ser también afín) que no modifica la norma del vector al que transforma, es decir \(\mathrm{det}(\mathbf{T})\)=1
si \(\mathbf{V}\in\mathbb{R}^{n \times n}\) y \(\mathbf{x}\in\mathbb{R}^n\) entonces pueden definirse ciertos subespacios de importancia según los resultados del mapeo de la transformación lineal
espacio nulo: el subespacio de todos los vectores que son mapeados al vector cero
Subespacios de importancia
espacio imagen: el subespacio de todos los vectores (distintos de cero) producidos por la aplicación de la transformación lineal
se cumple que
y se obtiene uno de los resultados más importantes del álgebra lineal
\(\mathbf{V}\) es invertible \(\Leftrightarrow \mathcal{N}(\mathbf{V})=\{\mathbf{0}\} \Leftrightarrow \mathcal{R}\{\mathbf{V}\}=\mathbb{R}^n\)
\(\Leftrightarrow \) las columnas de \(\mathbf{V}\) son linealmente independientes \(\Leftrightarrow \mathrm{det}(\mathbf{V})\ne0\)
Referencia MATLAB
x = [1; 2; 3]v = [-1, 0, 1, 2]w = [0.5, -8, 1]'x(2)x(1:2)x(end)x + wx' * wnorm(x, 2)cross(x, w)A = [1, 0, -1; -2, 3, 0; 0, 0, -0.5]A(2, 3)A(:, 2:end)A'det(A)I = eye(3)zeros(2, 5)A^(-1)
I/A
inv(A)A * IA = [1, 0, -1; -2, 3, 0; 0, 0, -0.5]null(A)orth(A)rank(A)