Cinemática de cuerpos rígidos

BE3027 - Robótica Médica

¿Por qué?

{^I}\mathbf{T}_B= \begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix}

¿Qué es la transformación homogénea?

{^I}\mathbf{T}_B= \begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix}

matriz de rotación

orientación de \(\{B\}\) con respecto a \(\{I\}\)

vectores de los ejes de coordenadas para \(\{B\}\)

{^I}\mathbf{T}_B= \begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix}

vector de traslación

posición de \(\{B\}\) con respecto a \(\{I\}\)

coordenadas del origen de \(\{B\}\)

{^I}\mathbf{T}_B= \begin{bmatrix} {^I}\mathbf{R}_B & {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix}

ajuste por coordenadas homogéneas

¿Coordenadas homogéneas?

{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{ {^B}\mathbf{p} \right\}
\equiv {^I}\tilde{\mathbf{p}}={^I}\mathbf{T}_B {^B}\tilde{\mathbf{p}}

¿Coordenadas homogéneas?

{^I}\mathbf{p}={^I}\mathcal{T}_B\left\{ {^B}\mathbf{p} \right\}
\equiv {^I}\tilde{\mathbf{p}}={^I}\mathbf{T}_B {^B}\tilde{\mathbf{p}}

vectores en coordenadas homogéneas

\tilde{\mathbf{p}}=\begin{bmatrix} \mathbf{p} \\ 1 \end{bmatrix}

Las matrices de rotación junto con la multiplicación de matrices forman el grupo especial ortogonal

caso 2D

caso 3D

{^I}\mathbf{R}_B \in
SO(2) \subset \mathbb{R}^{2 \times 2}
SO(3) \subset \mathbb{R}^{3 \times 3}
{^I}\mathbf{R}_B {^B}\mathbf{R}_C = {^I}\mathbf{R}_C

multiplicación entre rotaciones produce rotaciones

\left({^I}\mathbf{R}_B\right)^{-1}={^I}\mathbf{R}_B^\top\equiv {^B}\mathbf{R}_I
\mathrm{det}\left({^I}\mathbf{R}_B\right)=1

son matrices ortogonales

Las matrices de transformación homogénea junto con la multiplicación de matrices forman el grupo especial euclideano

caso 2D

caso 3D

{^I}\mathbf{T}_B \in
SE(2) \subset \mathbb{R}^{3 \times 3}
SE(3) \subset \mathbb{R}^{4 \times 4}
{^I}\mathbf{T}_B {^B}\mathbf{T}_C = {^I}\mathbf{T}_C

multiplicación entre transformaciones produce transformaciones

NO son matrices ortogonales

{^B}\mathbf{T}_I \equiv \left({^I}\mathbf{T}_B\right)^{-1} = \begin{bmatrix} {^I}\mathbf{R}_B^\top & -{^I}\mathbf{R}_B^\top {^I}\mathbf{o}_B \\ \mathbf{0} & 1 \end{bmatrix} \ne {^I}\mathbf{T}_B^\top

Cinemática de cuerpos rígidos en 2D

x
y
\{I\}
x_B
y_B
\{B\}
(x,y)
\theta
{^I}\mathbf{T}_B=\begin{bmatrix} \cos\theta & -\sin\theta & x \\ \sin\theta & \cos\theta & y \\ 0 & 0 & 1 \end{bmatrix}

3 grados de libertad

\in \mathbb{R}^{3 \times 3}
IT_B = [ cos(theta), -sin(theta), x; 
         sin(theta),  cos(theta), y; 
                  0,           0, 1 ];
                  
IT_B = transl2(x, y) * trot2(theta); % Robotics Toolbox

Ejemplo

Suponga que un sensor de distancia instalado en un vehículo detecta una señal de tránsito en la posición \(\begin{bmatrix} 1 & 3 \end{bmatrix}^\top\). Este vehículo se encuentra en la posición \(\begin{bmatrix} 2 & 0 \end{bmatrix}^\top\) en el marco inercial (o global) con una orientación de \(\pi/3\). ¿Cuáles son las coordenadas globales de la señal de tránsito?​

>> be3027_clase2_vehiculo2d.mlx

Cinemática de cuerpos rígidos en 3D

{^I}\mathbf{T}_B=\begin{bmatrix} r_{11} & r_{12} & r_{13} & x \\ r_{21} & r_{22} & r_{23} & y \\ r_{31} & r_{32} & r_{33} & z \\ 0 & 0 & 0 & 1 \end{bmatrix}
{^I}\mathbf{T}_B=\begin{bmatrix} r_{11} & r_{12} & r_{13} & x \\ r_{21} & r_{22} & r_{23} & y \\ r_{31} & r_{32} & r_{33} & z \\ 0 & 0 & 0 & 1 \end{bmatrix}

extensión lógica al caso 3D

{^I}\mathbf{T}_B=\begin{bmatrix} r_{11} & r_{12} & r_{13} & x \\ r_{21} & r_{22} & r_{23} & y \\ r_{31} & r_{32} & r_{33} & z \\ 0 & 0 & 0 & 1 \end{bmatrix}

extensión lógica al caso 3D

ya NO tiene interpretación (única)

{^I}\mathbf{T}_B=\begin{bmatrix} r_{11} & r_{12} & r_{13} & x \\ r_{21} & r_{22} & r_{23} & y \\ r_{31} & r_{32} & r_{33} & z \\ 0 & 0 & 0 & 1 \end{bmatrix}

extensión lógica al caso 3D

ya NO tiene interpretación (única)

próxima clase

Aún cuando no podamos interpretar la rotación, podemos generar la transformación mediante transformaciones (activas) elementales

\mathbf{T}_x(a)=\begin{bmatrix} 1 & 0 & 0 & a \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Tx = transl(a, 0, 0)
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_x(a)

Traslación en \(x\)

\mathbf{T}_y(a)=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & a \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Ty = transl(0, a, 0)
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_y(a)

Traslación en \(y\)

\mathbf{T}_z(a)=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & a \\ 0 & 0 & 0 & 1 \end{bmatrix}
Tz = transl(0, 0, a)
\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_z(a)

Traslación en \(z\)

\mathbf{T}_{R_x}(\theta)=\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Trx = trotx(theta)
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_{r_x}(\theta)

Rotación en \(x\)

\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\mathbf{T}_{r_y}(\theta)=\begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta & 0 & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Try = troty(theta)
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_{r_y}(\theta)

Rotación en \(y\)

\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}
\mathbf{T}_{r_z}(\theta)=\begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \\ \sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
Trz = trotz(theta)
{^I}\mathbf{T}_B={^I}\mathbf{T}_A\mathbf{T}_{r_z}(\theta)

Rotación en \(z\)

\{A\}
x_A
y_A
z_A
x_B
y_B
z_B
\{B\}

¿Cuál es la pose de \(\{B\}\) con respecto de \(\{A\}\)?

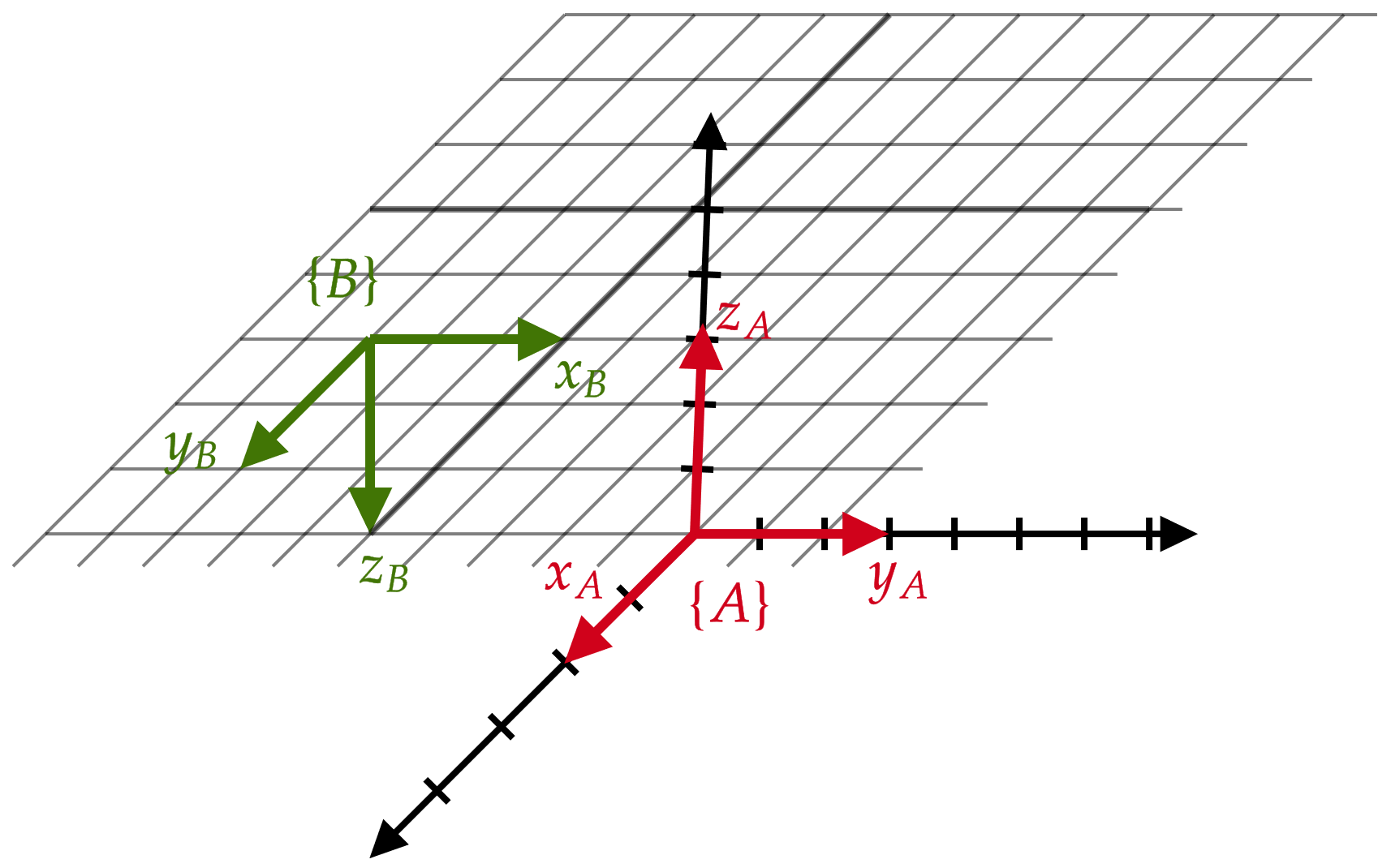
>> be3027_clase2_transformaciones.m