BE3027 - Lecture 7 (2024)

\mathbf{q}

\mathbf{q}

\mathcal{K}\left(\mathbf{q}\right) \subseteq {^B}\mathbf{T}_E(\mathbf{q})

\mathcal{K}\left(\mathbf{q}\right) \subseteq {^B}\mathbf{T}_E(\mathbf{q})

\mathcal{K}:\mathcal{C}\to \mathcal{T}

\mathcal{K}:\mathcal{C}\to \mathcal{T}

cinemática directa

\dot{\mathbf{q}}

\dot{\mathbf{q}}

{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}

{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}

{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}

{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}

cinemática diferencial

\dot{\mathbf{q}}

\dot{\mathbf{q}}

{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}

{^B}\mathcal{V}_E=\begin{bmatrix} {^B}\mathbf{v}_E \\ {^B}\boldsymbol{\omega}_{BE} \end{bmatrix}

{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}

{^B}\mathcal{V}_E=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}

cinemática diferencial

¿A qué queremos llegar?

\mathbf{q}

\mathbf{q}

\subseteq {^B}\mathbf{T}_E(\mathbf{q})

\subseteq {^B}\mathbf{T}_E(\mathbf{q})

\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}

\mathcal{K}^{-1}:\mathcal{T}\to \mathcal{C}

cinemática inversa

especificación de la tarea

(se tiene)

referencias para los servos

(se quiere)

A pesar que el planteamiento es claro, se tiene un problema considerable

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

A pesar que el planteamiento es claro, se tiene un problema considerable

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

\mathcal{K}(\mathbf{q})

\mathcal{K}(\mathbf{q})

(en general) función extremadamente no lineal de la configuración

A pesar que el planteamiento es claro, se tiene un problema considerable

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

\mathcal{K}^{-1}\left( \mathcal{K}(\mathbf{q})\right)=\mathbf{q}

\mathcal{K}^{-1}

\mathcal{K}^{-1}

encontrar este mapeo resulta muy difícil y en muchos casos NO existe solución analítica

Ejemplo: cinemática inversa analítica

\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \end{bmatrix} \in \mathbb{R}^2

\mathbf{q}=\begin{bmatrix} q_1 \\ q_2 \end{bmatrix} \in \mathbb{R}^2

\mathcal{T} \sim (x,y) \subset SE(2)

\mathcal{T} \sim (x,y) \subset SE(2)

espacio de configuración

espacio de tarea

Ejemplo: cinemática inversa analítica

\begin{array}{c|c|c|c} \theta_j & d_j & a_j & \alpha_j \\ \hline q_1 & 0 & a_1 & 0 \\ \hline q_2 & 0 & a_2 & 0 \\ \end{array}

\begin{array}{c|c|c|c} \theta_j & d_j & a_j & \alpha_j \\ \hline q_1 & 0 & a_1 & 0 \\ \hline q_2 & 0 & a_2 & 0 \\ \end{array}

R

manipulador RR

{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

\mathbf{J}(\mathbf{q})= \begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}

\mathbf{J}(\mathbf{q})= \begin{bmatrix} -a_1\sin(q_1)-a_2\sin(q_1 + q_2) & -a_2\sin(q_1 + q_2) \\ a_1\cos(q_1)+a_2\cos(q_1 + q_2) & a_2\cos(q_1 + q_2) \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 1 \end{bmatrix}

{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

{^B}\mathbf{T}_E(\mathbf{q})=\begin{bmatrix} \cos(q_1+q_2) & -\sin(q_1+q_2) & 0 & a_2\cos(q_1+q_2)+a_1\cos(q_1) \\ \sin(q_1+q_2) & \cos(q_1+q_2) & 0 & a_2\sin(q_1+q_2)+a_1\sin(q_1) \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}

\mathcal{K}\left(\mathbf{q}\right)= {^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}= \begin{bmatrix} a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ a_1\sin(q_1)+a_2\sin(q_1+q_2) \end{bmatrix}

\mathcal{K}\left(\mathbf{q}\right)= {^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}= \begin{bmatrix} a_1\cos(q_1)+a_2\cos(q_1+q_2) \\ a_1\sin(q_1)+a_2\sin(q_1+q_2) \end{bmatrix}

\Rightarrow \mathbf{q}= \mathcal{K}^{-1}\left({^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}\right)

\Rightarrow \mathbf{q}= \mathcal{K}^{-1}\left({^B}\begin{bmatrix} x_E(\mathbf{q}) \\ y_E(\mathbf{q}) \end{bmatrix}\right)

empleando trigonometría y métodos algebráicos

q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)

q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)

q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)

q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)

empleando trigonometría y métodos algebráicos

q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)

q_1=\mathrm{atan2}\left(\dfrac{y_E}{x_E}\right)-\mathrm{atan2}\left(\dfrac{a_2\sin(q_2)}{a_1+a_2\cos(q_2)}\right)

q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)

q_2=\arccos\left( \dfrac{x_E^2+y_E^2-a_1^2-a_2^2}{2 a_1a_2}\right)

$\arctan$ pero válida en $(-\pi, \pi]$ (programación)

las expresiones trigonométricas muestran múltiples soluciones al problema

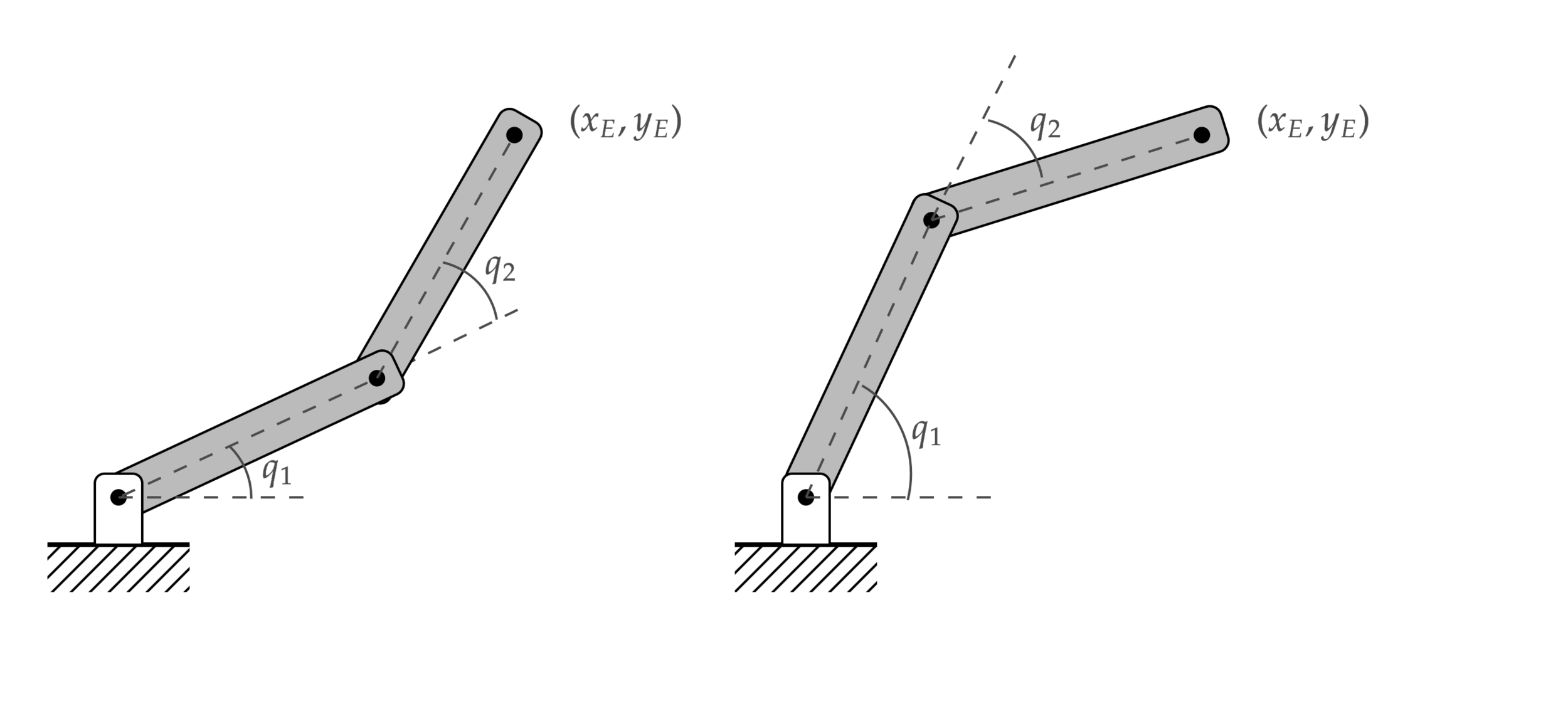
si bien hay casos en donde podemos encontrar la solución analítica, hacerlo no es tan buena idea

$\to$ expresiones complejas e individuales, incluso para manipuladores triviales

$\to$ solución dada en lazo abierto (no corrige errores)

¿Qué hacemos entonces?

emplear algoritmos basados en control (lazo cerrado) para encontrar la cinemática inversa de forma numérica

>> be3027_clase7_robotRR_ik.mlx

\mathbf{q}_0

\mathbf{q}_0

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_f

\mathbf{q}_f

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_f

\mathbf{q}_f

ikine

{^B}\mathbf{T}_E \to \mathbf{T}_d

{^B}\mathbf{T}_E \to \mathbf{T}_d

(en general)

\mathbf{q} \to \mathbf{q}_d

\mathbf{q} \to \mathbf{q}_d

NO necesariamente

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_f

\mathbf{q}_f

ikine

{^B}\mathbf{T}_E \to \mathbf{T}_d

{^B}\mathbf{T}_E \to \mathbf{T}_d

(en general)

\mathbf{q} \to \mathbf{q}_d

\mathbf{q} \to \mathbf{q}_d

NO necesariamente

Para que el problema tenga solución y se acople a los GDL del robot, la Robotics Toolbox emplea la noción de máscaras

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_0

\mathbf{q}_0

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_0={^B}\mathbf{T}_E(\mathbf{q}_0)= \begin{bmatrix} {^B}\mathbf{R}_E(\mathbf{q}_0) & {^B}\mathbf{o}_E(\mathbf{q}_0) \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{q}_f

\mathbf{q}_f

ikine

{^B}\mathbf{T}_E \to \mathbf{T}_d

{^B}\mathbf{T}_E \to \mathbf{T}_d

(en general)

\mathbf{q} \to \mathbf{q}_d

\mathbf{q} \to \mathbf{q}_d

NO necesariamente

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

\mathbf{T}_d={^B}\mathbf{T}_E(\mathbf{q}_d)\\ =\begin{bmatrix} \mathbf{R}_d & \mathbf{o}_d \\ \mathbf{0} & 1 \end{bmatrix}

>> be3027_clase7_p560ik.m

idea fundamental (prestando atención sólo a la posición)

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

idea fundamental (prestando atención sólo a la posición)

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

\Delta {^B}\mathbf{o}_E=\mathbf{J}_v(\mathbf{q}) \Delta \mathbf{q}

\Delta {^B}\mathbf{o}_E=\mathbf{J}_v(\mathbf{q}) \Delta \mathbf{q}

\Rightarrow \Delta \mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}) \Delta {^B}\mathbf{o}_E

\Rightarrow \Delta \mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}) \Delta {^B}\mathbf{o}_E

idea fundamental (prestando atención sólo a la posición)

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

{^B}\mathbf{v}_E=\mathbf{J}_v(\mathbf{q})\dot{\mathbf{q}}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

\dfrac{\Delta {^B}\mathbf{o}_E}{\Delta t}=\mathbf{J}_v(\mathbf{q}) \dfrac{\Delta \mathbf{q}}{\Delta t}

\Delta {^B}\mathbf{o}_E=\mathbf{J}_v(\mathbf{q}) \Delta \mathbf{q}

\Delta {^B}\mathbf{o}_E=\mathbf{J}_v(\mathbf{q}) \Delta \mathbf{q}

\Rightarrow \Delta \mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}) \Delta {^B}\mathbf{o}_E

\Rightarrow \Delta \mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}) \Delta {^B}\mathbf{o}_E

pseudo-inversa del jacobiano >> pinv(Jv)

$\mathbf{T}_d\equiv$ meta

${^B}\mathbf{T}_E(\mathbf{q})$

efector final

el algoritmo debe llevar al efector final a la pose deseada o "meta"

$\mathbf{T}_d\equiv$ meta

${^B}\mathbf{T}_E(\mathbf{q})$

efector final

Nota 1: el robot sólo puede cambiar su configuración

Nota 2: por el momento nos interesa sólo la posición

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

¿Cuál es la discrepancia entre la posición deseada y la posición actual?

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

¿Cuál es la discrepancia entre la posición deseada y la posición actual?

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1)

¿Cuál es la discrepancia entre la posición deseada y la posición actual?

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1) \sim \Delta {^B}\mathbf{o}_E

\mathbf{e}_p=\mathbf{o}_d-{^B}\mathbf{o}_E(\mathbf{q}_1) \sim \Delta {^B}\mathbf{o}_E

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

¿Hacia dónde, potencialmente, puede moverse el robot?

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

configuración actual: $\mathbf{q}_1$

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

entonces el robot hace un movimiento pequeño tomando todo en consideración

configuración actual: $\mathbf{q}_2$

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

entonces el robot hace un movimiento pequeño tomando todo en consideración

configuración actual: $\mathbf{q}_2$

\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}

\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}

\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\ \Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p

\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\ \Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p

{^B}\mathbf{o}_E(\mathbf{q}_1)

{^B}\mathbf{o}_E(\mathbf{q}_1)

\mathbf{o}_d

\mathbf{o}_d

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

\mathbf{A}_v^{-1}(\mathbf{q}_1)=\left(\mathbf{J}_v(\mathbf{q}_1)\mathbf{J}^\top_v(\mathbf{q}_1)\right)^{-1}

entonces el robot hace un movimiento pequeño tomando todo en consideración

configuración actual: $\mathbf{q}_2$

\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}

\mathbf{q}_2=\mathbf{q}_1+\Delta\mathbf{q}

\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\ \Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p

\Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \Delta {^B}\mathbf{o}_E \\ \Delta\mathbf{q}=\mathbf{J}^\dagger_v(\mathbf{q}_1) \mathbf{e}_p

\mathbf{q}_2=\mathbf{q}_1+\mathbf{J}^\dagger_v(\mathbf{q}_1)\mathbf{e}_p

\mathbf{q}_2=\mathbf{q}_1+\mathbf{J}^\dagger_v(\mathbf{q}_1)\mathbf{e}_p

y se repite el proceso hasta que el error/discrepancia sea lo suficientemente pequeño

pueden obtenerse algoritmos similares pero para la orientación o la pose completa

\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger\left(\mathbf{q}_k\right)\mathbf{e}_k

\mathbf{q}_{k+1}=\mathbf{q}_k+\mathbf{J}^\dagger\left(\mathbf{q}_k\right)\mathbf{e}_k

Todo algoritmo de cinemática inversa cumple con la estructura

donde $\mathbf{q}_{k+1} \to \mathbf{q}_d$ conforme incrementa el número de iteraciones