Formación de imágenes

MT3006 - Robótica 2

¿Por qué?

Imágenes y pixeles






pixel
picture element
dos tipos de información
- Información espacial:
- ¿Qué implica la posición 2D del pixel con respecto de la situación real en 3D?
- ¿Qué información se conserva y cuál se pierde?
- Información sensorial:
- ¿Qué valores puede tomar un pixel?
- ¿Cuál es la relación de este valor con respecto del color?
La geometría detrás de la formación de imágenes
Una primera idea
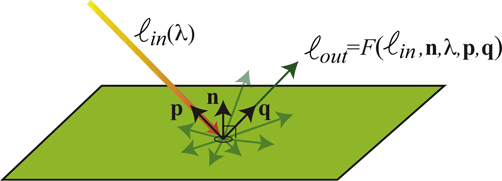
Una primera idea
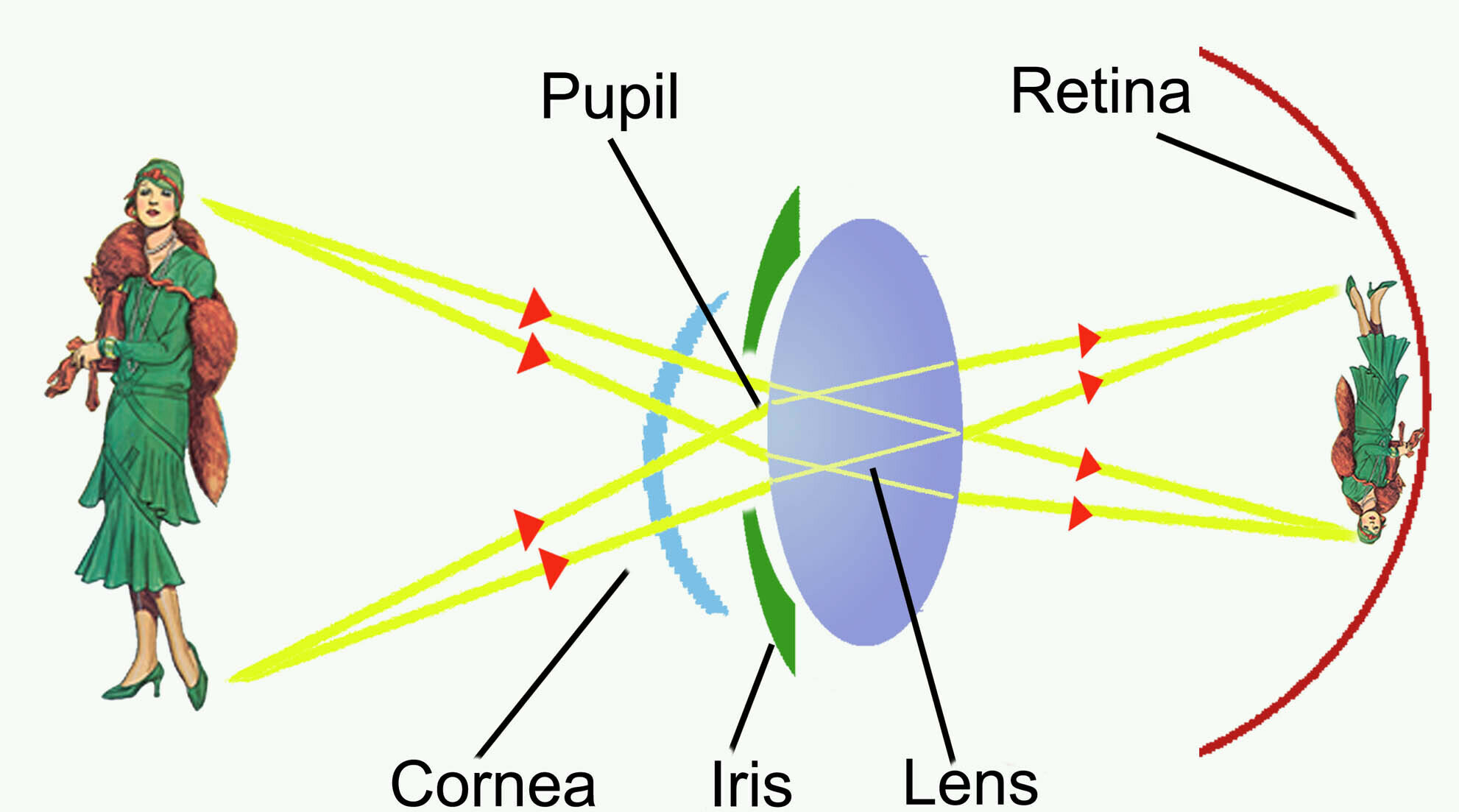
plano de imagen
pinhole
Pinhole camera o camera obscura

Formalizando esta situación
(arbitrario)
plano de imagen en \(\lambda z = -1\)
\(\Rightarrow \lambda = -1/z\)
coordenadas en el plano de imagen, pero invertidas
imagen no invertida
imagen invertida
proyección de perspectiva
Mejorando el modelo
pinhole
distancia focal \(f\)
para lentes delgados
distancia hacia el objeto
distancia hacia el plano de imagen
si el objeto se encuentra lejos del lente
Cámara de lente delgado
pixeles
metros
Cámara de lente delgado
Detalles adicionales
pixeles a metros
[m/px]
cambio de centro
\(\mathbf{C}\) - matriz de cámara
\(\begin{bmatrix} f/\rho_w & 0 & u_0 & 0 \\ 0 & f/\rho_h & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \) - matriz de parámetros intrínsecos
\({^C}\mathbf{T}_I \) - matriz de parámetros extrínsecos
>> mt3006_clase1_modelo_camara.m
¿Aún más detalles?

barrel radial distortion
pincushion radial distortion



Calibración de cámara
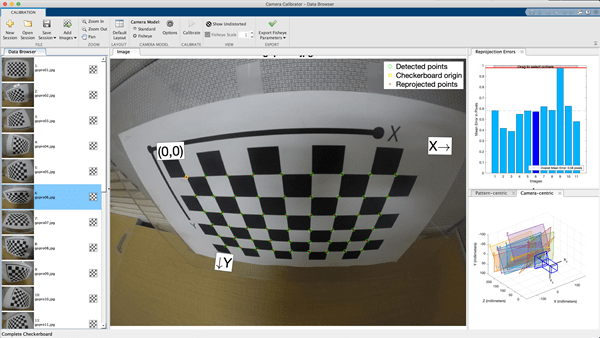
Calibración de cámara

Perspective-\(n\)-Point
(en general)
Consecuencias del mapeo

Consecuencias del mapeo

- 3D a 2D (pérdida de información).
- Rectas a rectas.
- Paralelas se intersecan en el horizonte.
- No se conserva el tamaño.
- Cónicas a cónicas.
- Mapeo NO es 1 a 1, \(\mathbf{C}\in\mathbb{R}^{3 \times 4}\).
- No preserva la forma.
¿Qué ocurre con el color?
Sensores de imagen



filtro (mosaico) de Bayer




Escala de grises


resolución de 8 bits
(uint8)
Escala de grises
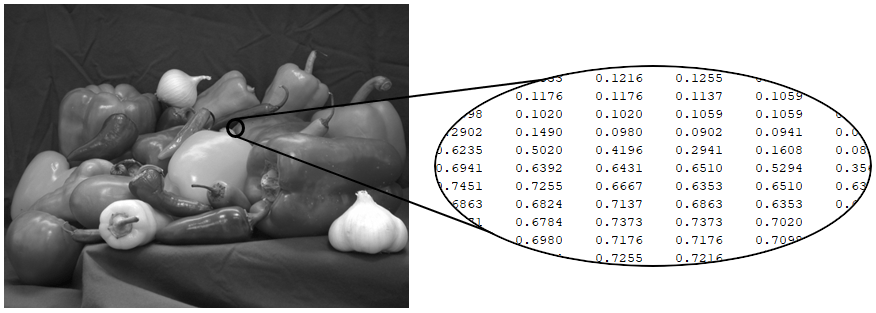

resolución de 8 bits
(uint8)
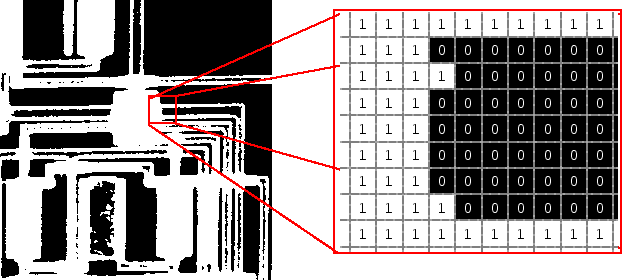
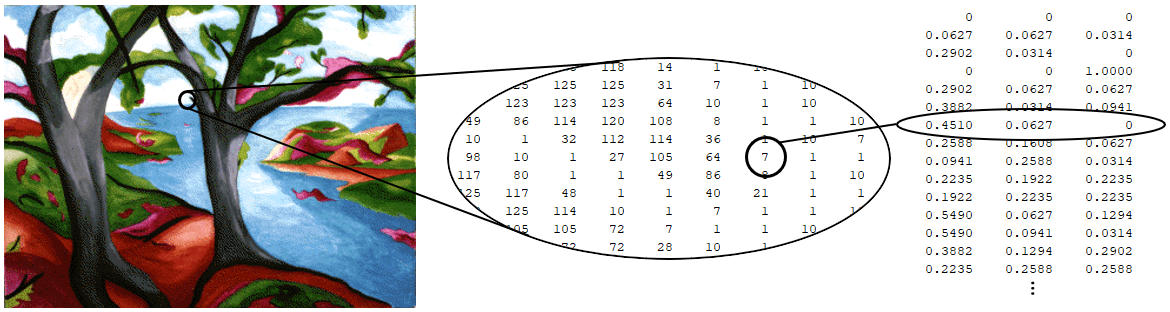
imágenes binarias
mapas de color
Imágenes a color y espacios de color


resolución de 24 bits
espacio de color RGB
Otros espacios de color



HSV
HSL
Entre otros como:
- CMYK
- YCbCr
- CIELAB (L*a*b*)
Referencias
- A. Torralba et al., Foundations of Computer Vision, bloques I y II.
- R. Klette, Concise Computer Vision, capítulo 6.