El filtro de Kalman y sus variantes

MT3006 - Robótica 2

¿Por qué no es suficiente el filtro complementario?

Necesitamos una herramienta que lidie directamente con la naturaleza estocástica del problema
Un flashback a control moderno
controlador lineal
state feedback
retroalimentación negativa
observador de estado
¿Qué es?
¿Cuándo funciona?
(valor) estimado del estado
Un flashback a control moderno
es un estimador
sistema que genera estimados | estimaciones
Según Luenberger
Un flashback a control moderno
Observadores de Luenberger
predicción
emplea lo que se conoce del sistema
corrección
emplea las mediciones para corregir la predicción
matriz de ganancias \(\in\mathbb{R}^{n \times p}\)
mediciones
salida según el modelo LTI \(\hat{\mathbf{y}}=\mathbf{C}\hat{\mathbf{x}}\)
Pero existe otra manera de interpretar el problema, desde una perspectiva de estimación
¿Estimación?
considera dos problemas
considera dos problemas
smoothing
¿Estimación?
considera dos problemas
smoothing
filtering
¿Estimación?
considera dos problemas
smoothing
filtering
queremos que sea en tiempo real
¿Estimación?
puede ser una ventana
Filtrado bajo la propiedad de Markov
Filtrado bajo la propiedad de Markov
toda la información del pasado está contenida en el estado (memoria)
permite entonces mediante la regla de Bayes
Filtrado bajo la propiedad de Markov
toda la información del pasado está contenida en el estado (memoria)
permite entonces mediante la regla de Bayes
Filtrado bajo la propiedad de Markov
toda la información del pasado está contenida en el estado (memoria)
modelo de medición
permite entonces mediante la regla de Bayes
Filtrado bajo la propiedad de Markov
toda la información del pasado está contenida en el estado (memoria)
permite entonces mediante la regla de Bayes
Filtrado bajo la propiedad de Markov
toda la información del pasado está contenida en el estado (memoria)
dinámica o modelo de proceso
Entonces, el filtro de Kalman puede interpretarse tanto como un observador de estado como un filtro Bayesiano
Entonces, el filtro de Kalman puede interpretarse tanto como un observador de estado como un filtro Bayesiano
veamos los detalles...
Una situación familiar...
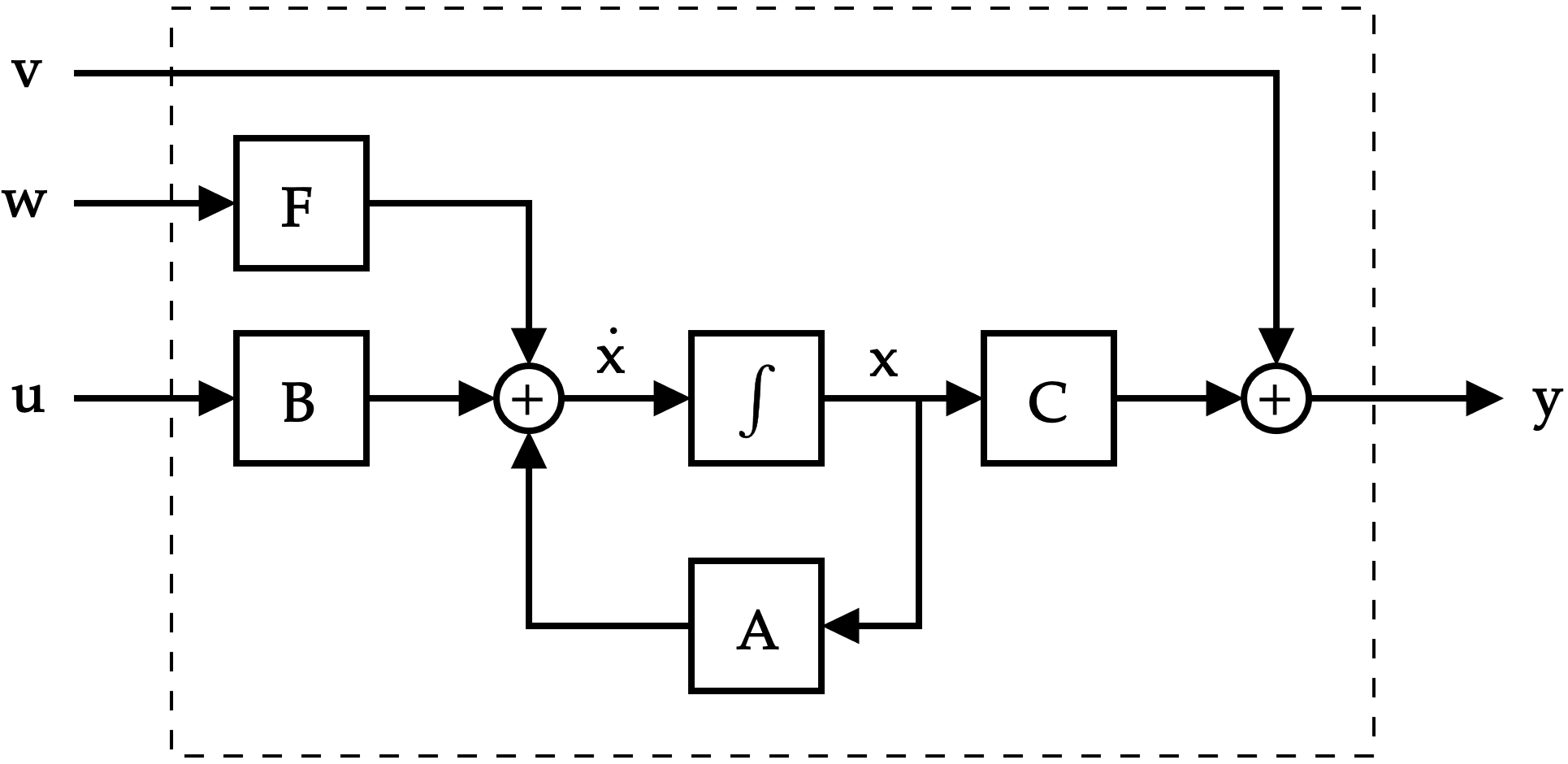
Una situación familiar...
...pero en tiempo discreto
permite matrices variantes en el tiempo
...pero en tiempo discreto
ruido de proceso
vector de ruido blanco
ruido de medición
vector de ruido blanco
...pero en tiempo discreto
aunque se permite que cambie la varianza en el tiempo, no es lo típico
...pero en tiempo discreto
aunque se permite que cambie la varianza en el tiempo, no es lo típico
¿Por qué tiempo discreto?
Porque el filtro puede separarse en etapas: predicción + corrección


el filtro devuelve

el filtro devuelve

encontrando la ganancia de Kalman \(\mathbf{L}_k\) que minimiza la varianza \(\mathbf{P}_k\) del error de estimación
\(\mathbf{e}_k=\hat{\mathbf{x}}-\mathbf{x}_k\)

se separa a \(\hat{\mathbf{x}}_k\) en dos (igual que a \(\mathbf{P}_k\)):
\(\hat{\mathbf{x}}_{k|k-1}\) a-priori (sin mediciones)
\(\hat{\mathbf{x}}_{k|k}\) a-posteriori (con mediciones)

condición inicial (si se conoce) o un estimado de la misma

certeza con la que se conoce la condición inicial
\(\mathbf{P}_{0|0}=E\left\{\mathbf{x}_0\mathbf{x}_0^\top\right\}=\sigma_e^2\mathbf{I}\)


innovación
\(\mathbf{z}_k=\mathbf{y}_k-\mathbf{C}[k]\hat{\mathbf{x}}_{k|k-1}\)

covarianza de la innovación
\(\mathbf{S}[k]=\mathbf{Q}_v[k]+\mathbf{C}[k]\mathbf{P}_{k|k-1}\mathbf{C}[k]^\top\)

intuición: >> mt3006_clase11_kalman1d.m

ejemplo: >> mt3006_clase11_kalman_fusion.mlx
El filtro de Kalman Extendido (EKF)
extiende el filtro al caso no lineal
redefiniendo la predicción y corrección de estado y generando las matrices \(\mathbf{A}, \mathbf{B}, \mathbf{F}, \mathbf{C}\) mediante linealización (jacobianos)


Regresando a fusión de sensores
Predicción
Corrección
medición
sensores propioceptivos
sensores exteroceptivos
filtro de Kalman
Predicción
Corrección
medición
sensores propioceptivos
sensores exteroceptivos
filtro de Kalman
ambos son modelos de medición (sensores)*
ambos son modelos de medición (sensores)*
Predicción
Corrección
medición
sensores propioceptivos
sensores exteroceptivos
filtro de Kalman
* se colocan los propioceptivos en la predicción dado que estos típicamente miden cantidades diferenciales | incrementales, por lo mismo presentan "dinámica".
supongamos que quiere encontrarse cierta cantidad \(z\) y la misma se mide con dos sensores
Ejemplo
Referencias
- MT3006 - Localización y mapeo en robótica móvil.pdf
- Kok et. al, Using Inertial Sensors for Position and Orientation Estimation.
Predicción
Corrección
medición
sensores propioceptivos
sensores exteroceptivos
filtro de Kalman
IMPORTANTE: diferenciar el uso del filtro como filtro vs como observador