Localización empleando odometría, sensores inerciales y sistemas de posicionamiento I

MT3006 - Robótica 2

¿Qué estamos buscando?

plantear el problema de localización bajo la perspectiva del filtro de Kalman
plantear el problema de localización bajo la perspectiva del filtro de Kalman
estimación de pose
plantear el problema de localización bajo la perspectiva del filtro de Kalman
predicción + corrección
estimación de pose
plantear el problema de localización bajo la perspectiva del filtro de Kalman
predicción + corrección
propiocepción
exterocepción
estimación de pose
plantear el problema de localización bajo la perspectiva del filtro de Kalman
predicción + corrección
propiocepción
exterocepción
estimación de pose
Predicción de pose empleando dead-reckoning
Dead-reckoning
emplea la combinación de una posición (o pose) previamente determinada junto a un estimado de la velocidad (o aceleración) del robot para estimar la posición (o pose) actual del mismo
\(\equiv\) integración de recorrido
Dead-reckoning
consideraremos dos esquemas para efectuarlo, uno empleando odometría y otro típico en fusión de sensores inerciales
\(\equiv\) integración de recorrido
Odometría para robots con ruedas

Odometría para robots con ruedas



encoder rotacional magnético

\(r: \quad \) radio de la rueda
\(\ell: \quad\) distancia entre ruedas
\(\Delta\mathrm{tick}_R: \quad\) conteo diferencial de "muescas"
\(N: \quad \) número de "muescas" por revolución (debe tomar en consideración la caja reductora)
\(\delta_\rho: \quad\) distancia lineal recorrida
\(\delta_\theta: \quad\) distancia angular recorrida
¿Problema?
NO estamos tomando en consideración el posible drift en los encoders


puede reconstruirse la distancia lineal desde las revoluciones de la rueda
las irregularidades hacen que la rueda presente más revoluciones que las que debería


puede reconstruirse la distancia lineal desde las revoluciones de la rueda
las irregularidades hacen que la rueda presente más revoluciones que las que debería
¿Solución?
Modelar estas irregularidades como ruido (de proceso)
(se requiere un EKF)
Otros tipos de odometría
visual (cámaras)
láser (LiDAR)


Dead-reckoning con sensores inerciales
velocidad angular
fuerza externa específica
aceleración
posición
orientación
rotar
remover gravedad
Dead-reckoning con sensores inerciales
velocidad angular
fuerza externa específica
aceleración
posición
orientación
rotar
remover gravedad
predicción
(con propiocepción)
Dead-reckoning con sensores inerciales
velocidad angular
fuerza externa específica
aceleración
posición
orientación
rotar
remover gravedad
próxima clase...
corrección
(con exterocepción)
Estimando posición con acelerómetros
la IMU más simple
= 3 acelerómetros
+ 3 giroscopios
Estimando posición con acelerómetros
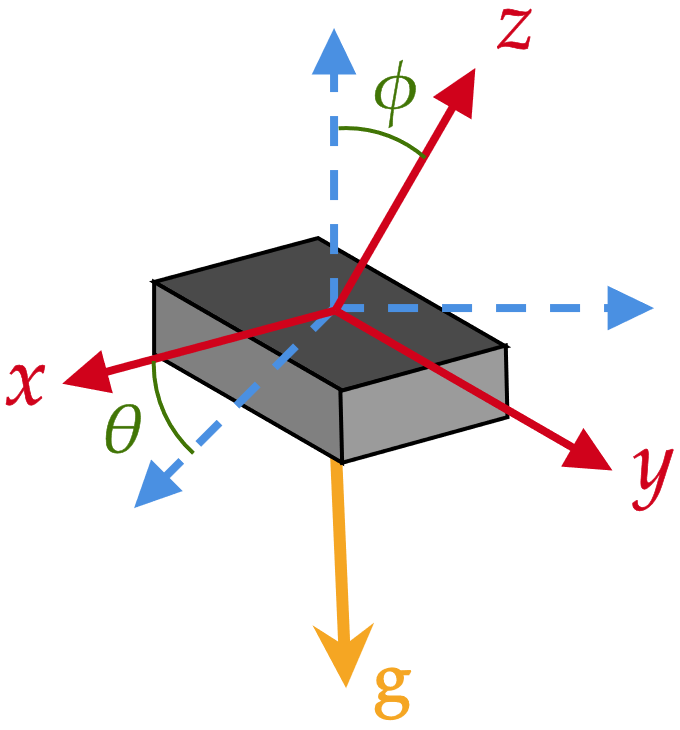
modelo considerado para un acelerómetro de tres ejes
ruido de medición
bias o deriva
Estimando posición con acelerómetros
modelo considerado para un acelerómetro de tres ejes
ruido de medición
bias o deriva
OJO
Estimando posición con acelerómetros
modelo considerado para un acelerómetro de tres ejes
ruido de medición
bias o deriva
OJO
claramente esta aceleración NO puede sólo integrarse
\(\Rightarrow\) se emplea un truco para poder encontrar un "modelo de proceso" que genere las mediciones
mediciones como entrada
necesita la orientación
necesita el bias \(\to\) puede estimarse
si se considera por aparte (estados | procesos distintos) la estimación de orientación, esto (discretizado) corresponde a las matrices \(\mathbf{A}[k], \mathbf{B}[k]\) y \(\mathbf{F}[k]\) de un sistema LTV, y se emplea el filtro de Kalman para la fusión de sensores
si se considera en conjunto la estimación de posición y orientación, entonces esto (discretizado) es no lineal y deberá emplearse un EKF con los jacobianos de la dinámica del proceso
Estimando orientación con giroscopios
modelo considerado para un giroscopio de tres ejes
ruido de medición
bias o deriva
+ discretización...
*
+ discretización...
cuidado, no es el mejor modelo* porque asume ángulos de roll, pitch y yaw
una mejor opción es emplear cuaterniones unitarios (con rotación referenciada con respecto al marco del sensor)
+ discretización y recordando re-normalizar los cuaterniones para que sean unitarios
+ discretización y recordando re-normalizar los cuaterniones para que sean unitarios
esto funciona sin problemas, pero la tendencia actual es emplear un algoritmo de optimización llamado filtro de Madgwick para estimar la orientación
¿Por qué no podemos quedarnos sólo con estas mediciones?
se necesita hacer corrección empleando sensores exteroceptivos
Referencias
- MT3006 - Localización y mapeo en robótica móvil.pdf
- Kok et. al, Using Inertial Sensors for Position and Orientation Estimation.
- https://ahrs.readthedocs.io/en/latest/filters.html.