Técnicas clásicas de visión por computadora I

MT3006 - Robótica 2

¿Por qué?

Procesamiento a nivel pixel
Thresholding

imagen binaria
(forma una máscara)
Thresholding

threshold
Thresholding
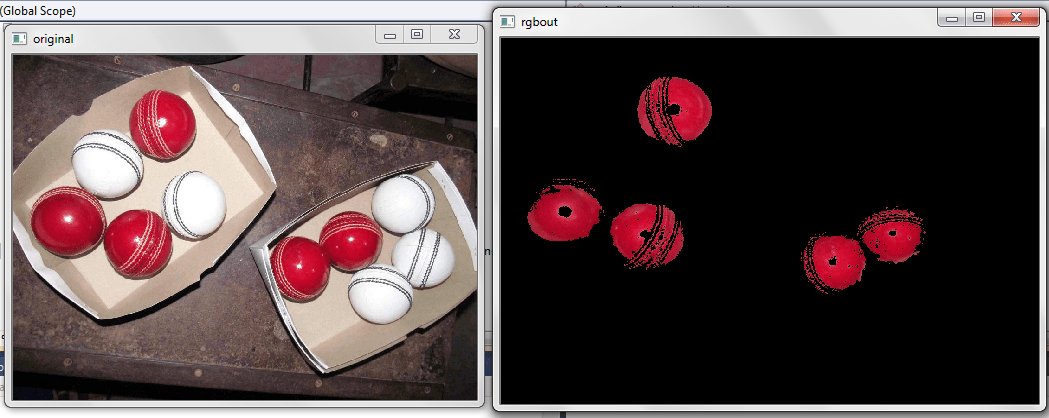
imagen luego de aplicar la máscara de color
Thresholding

imagen luego de aplicar la máscara de color
Thresholding

o bien (por ejemplo)
Thresholding

o bien (por ejemplo)
color de interés

Histogramas

Equalización de histograma

Equalización de histograma

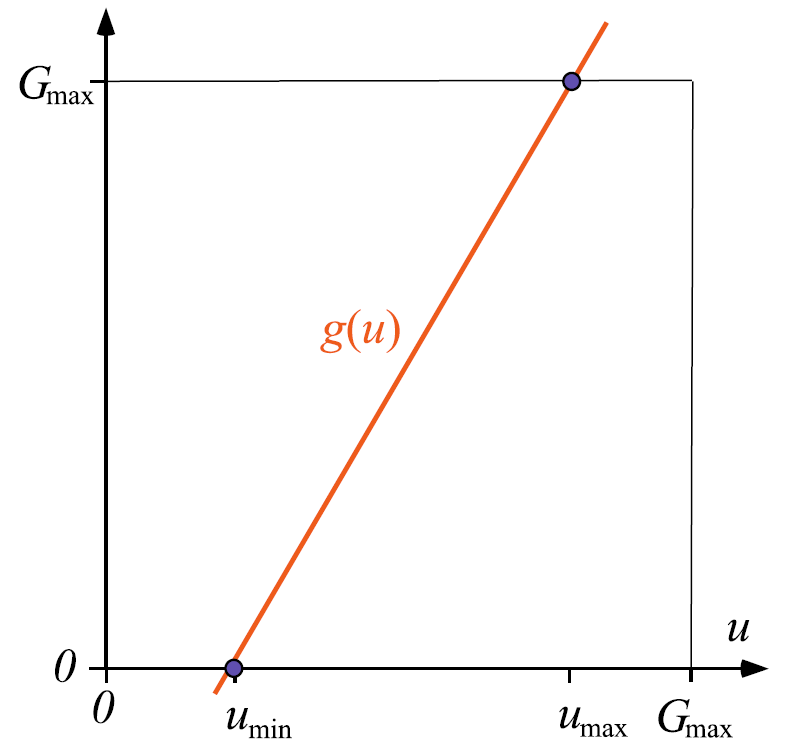
Procesamiento a nivel local
Estadísticas básicas

también aplican a nivel global
Filtrado LTI \(\equiv\) Convolución


Filtrado LTI \(\equiv\) Convolución


kernel de \((2k+1)\times(2k+1)\)
factor de escalamiento tal que \(\displaystyle \sum_i \sum_j |w_{ij}|=S\)
Filtrado LTI \(\equiv\) Convolución


kernel de \((2k+1)\times(2k+1)\)
factor de escalamiento tal que \(\displaystyle \sum_i \sum_j |w_{ij}|=S\)
si el kernel es simétrico entonces
correlación cruzada en 2D
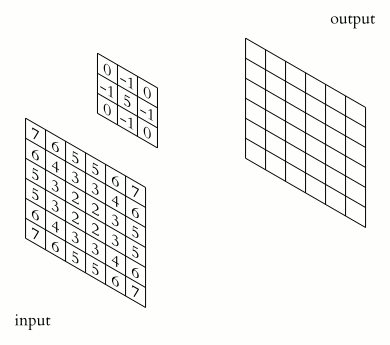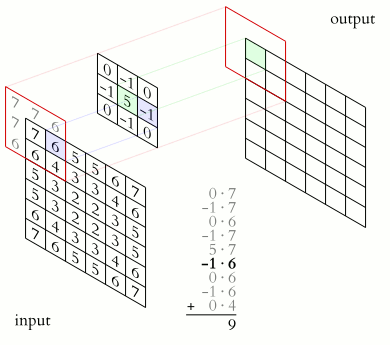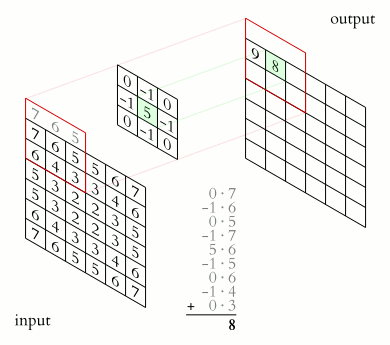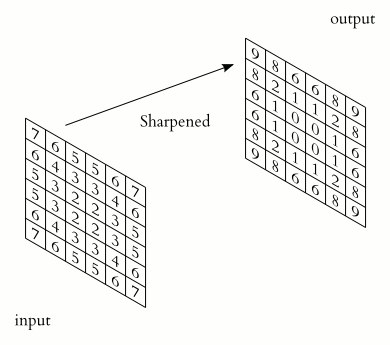
Procedimiento
Padding (efectos en los bordes)

Convolución vs correlación
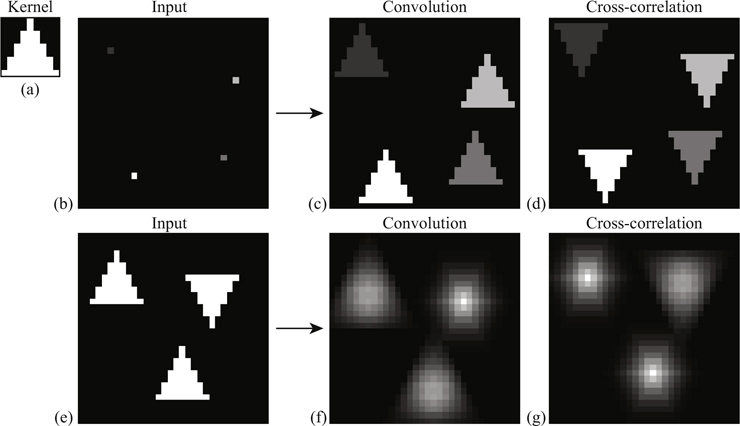
Convolución vs correlación

puede emplearse (normalizada) para hacer template matching
Kernels para suavizado (smoothing)
box filter

ej: \(3\times 3\)
\(S=9\) en este caso
Kernels para suavizado (smoothing)
Gaussian filter
bajo esta perspectiva el box filter corresponde a una distribución uniforme, también pueden emplearse otras distribuciones como la binomial

Aplicaciones de suavizado
de-noising


remoción de detalles
\(\Rightarrow\) suavizado \(\equiv\) filtrado pasa-bajas
Afilado (sharpening)
operación contraria al suavizado
\(\equiv\) filtrado pasa-altas \(\approx\) resaltado de detalles

sharpen filter (ejemplo)


puede emplearse suavizado para obtener afilado mediante unsharp masking
factor de escalamiento
versión suavizada de \(I\)
residual:

De detalles a bordes
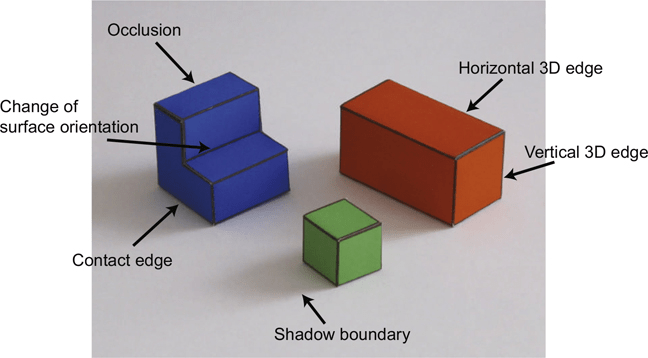

perfiles de intensidad
De detalles a bordes


perfiles de intensidad
discontinuidades \(\Rightarrow\) bordes
entonces pueden emplearse derivadas para detectarlos

gradiente
Laplaciano
Kernels para calcular derivadas
en imágenes el \(\delta\) más pequeño es 1, es decir, un pixel
Kernels para calcular derivadas
en imágenes el \(\delta\) más pequeño es 1, es decir, un pixel
kernels de Roberts
Derivadas y ruido

Roberts
Suavizado + Roberts
\(\Rightarrow\) Sobel
Kernels para calcular derivadas
kernels de Sobel
= derivada con \(\delta=2\) + suavizado con binomial


simple y decente, pero con bordes "de más" con diferente intensidad
¿Ideal? Imagen binaria sólo con los bordes más fuertes y con un grosor uniforme \(\Rightarrow\) detector de bordes de Canny
Canny edge detection

Canny edge detection
- Estimación del gradiente de la imagen.
- Se calcula la magnitud y la fase por pixel.
- La fase se aproxima | cuantifica a múltiplos de \(\pi/4\).
- Se realiza una supresión (local) de no-máximos para la magnitud, en la dirección de la fase.
- Se realiza una etapa de seguimiento de borde mediante thresholding e histéresis.
Canny edge detection
- Estimación del gradiente de la imagen.
- Se calcula la magnitud y la fase por pixel.
- La fase se aproxima | cuantifica a múltiplos de \(\pi/4\).
- Se realiza una supresión (local) de no-máximos para la magnitud, en la dirección de la fase.
- Se realiza una etapa de seguimiento de borde mediante thresholding e histéresis.
a pesar de haber detectores de bordes más modernos, el de Canny continúa siendo de los más útlies

Análisis de regiones y extracción (simple) de características
Análisis de regiones
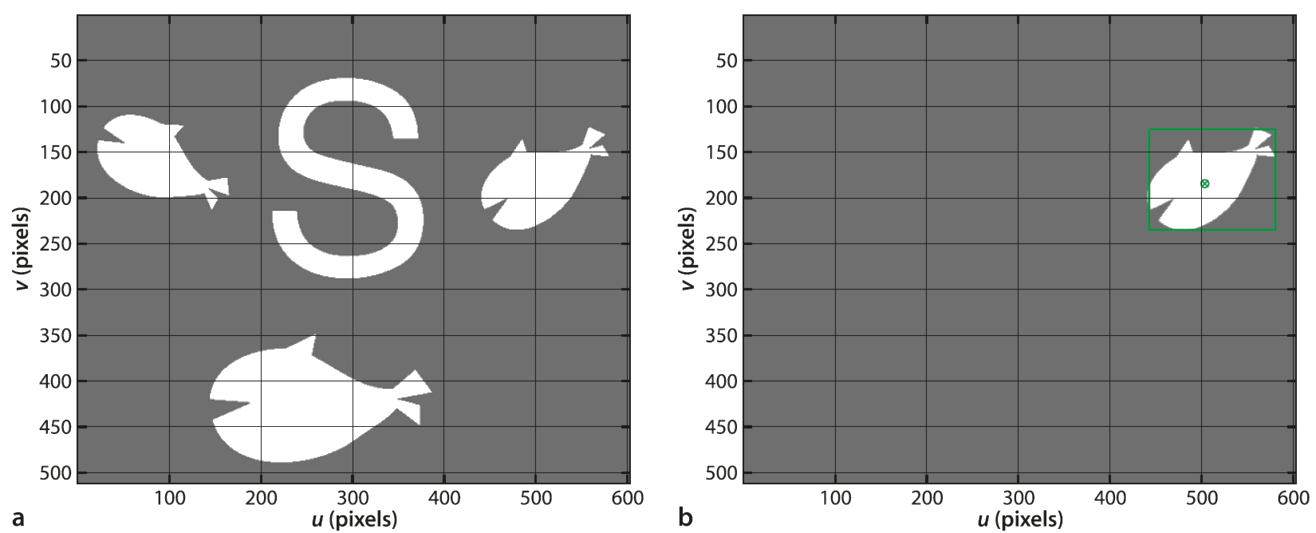
Análisis de regiones


imagen binaria
regiones
conformadas por conjuntos máximos de pixeles conectados
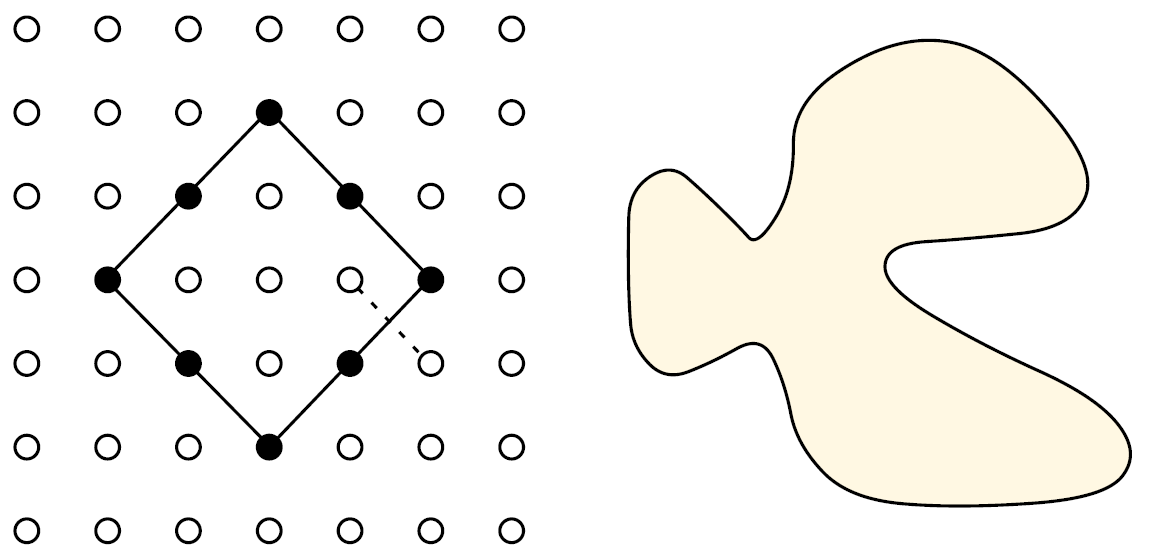
Conectividad y adyacencia

Conectividad y adyacencia

conjuntos de adyacencia
vecindarios
Conectividad y adyacencia

conjuntos de adyacencia
vecindarios
- El número de regiones puede cambiar dependiendo del tipo de conectividad considerada.
-
La topología de las regiones algunas veces no tiene "sentido" Euclideano.
Conteo según conectividad

Topología "extraña"


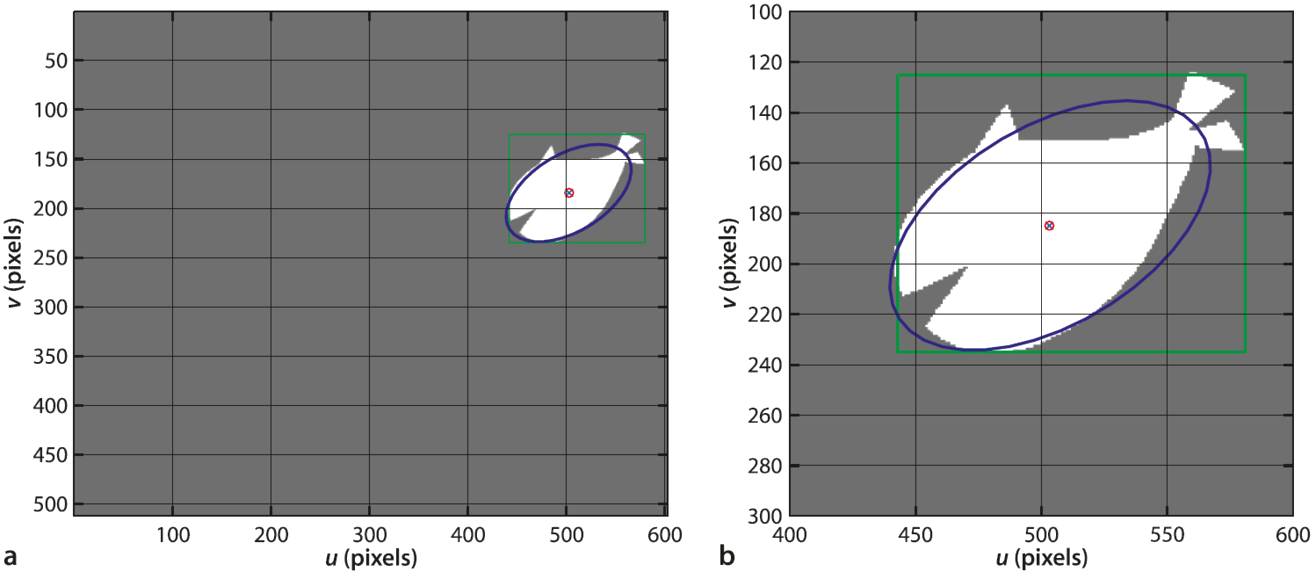
Análisis empleando momentos
Detección de líneas y círculos
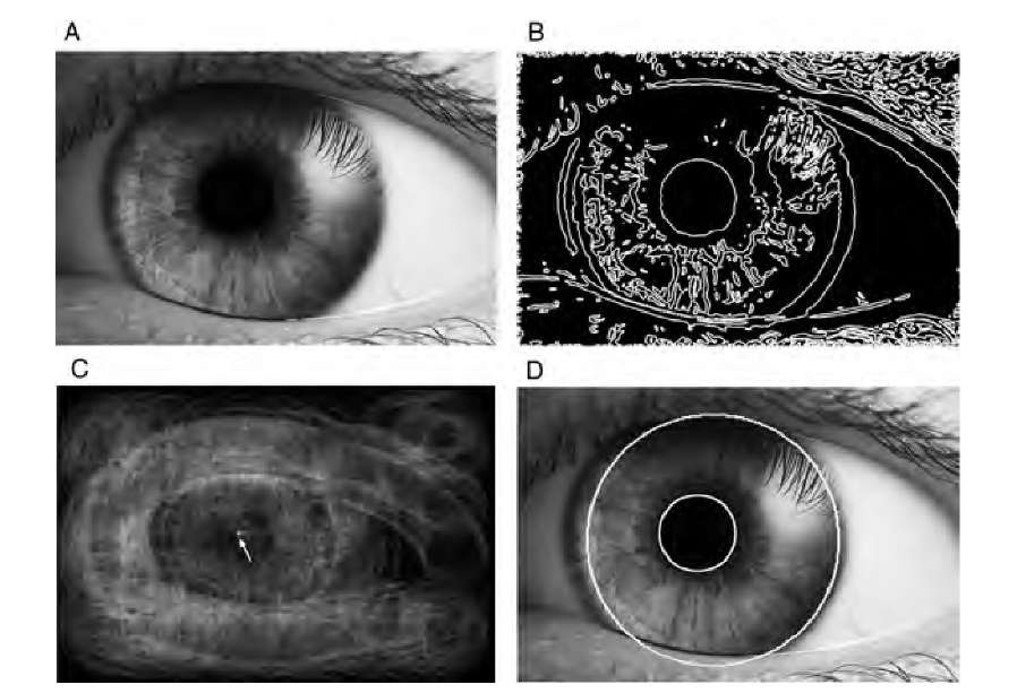

Transformada de Hough
Transformada de Hough para líneas
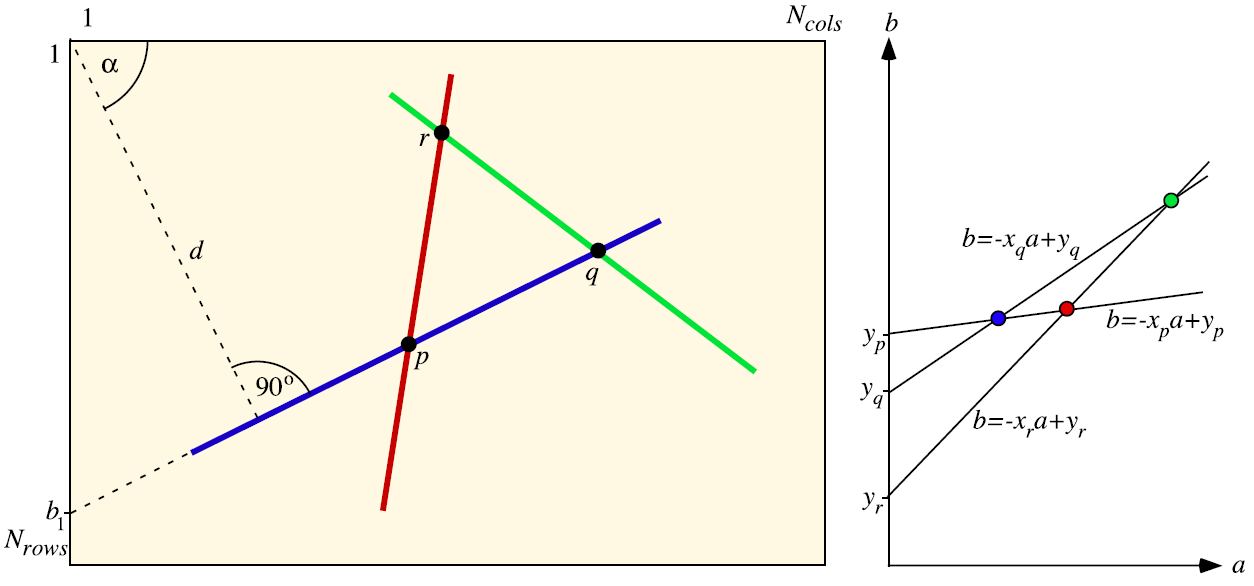
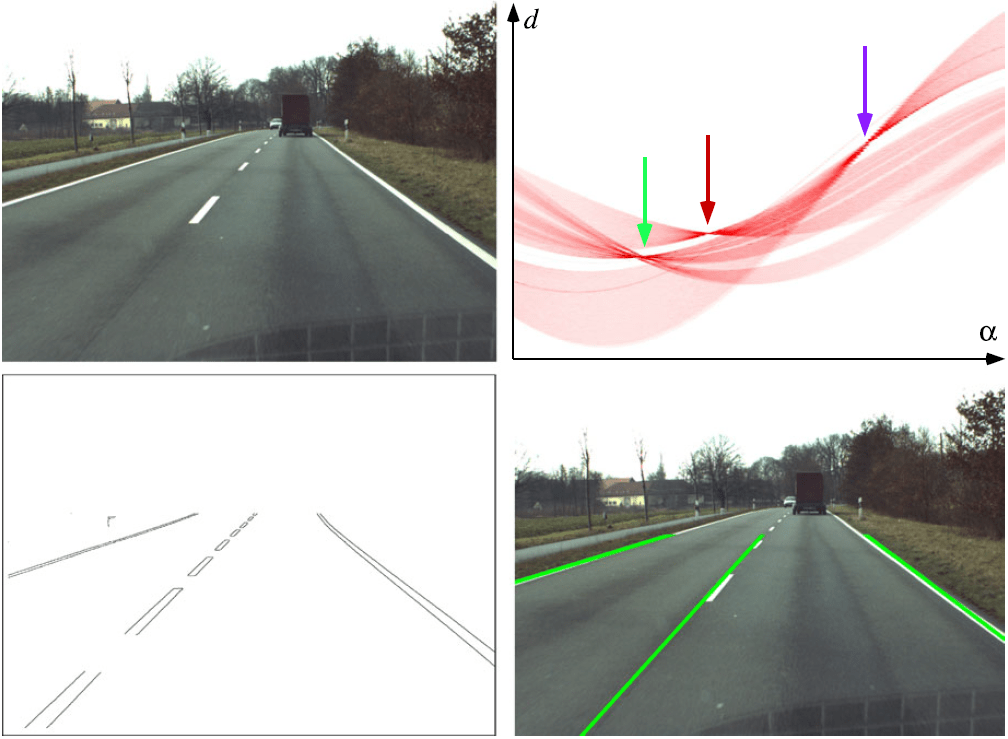
Segmentación


Referencias
- A. Torralba et al., Foundations of Computer Vision, bloques IV y V.
- R. Klette, Concise Computer Vision, capítulos 2, 3 y 5.
Detector de esquinas de Harris
