Control basado en visión

MT3006 - Robótica 2

¿Por qué?

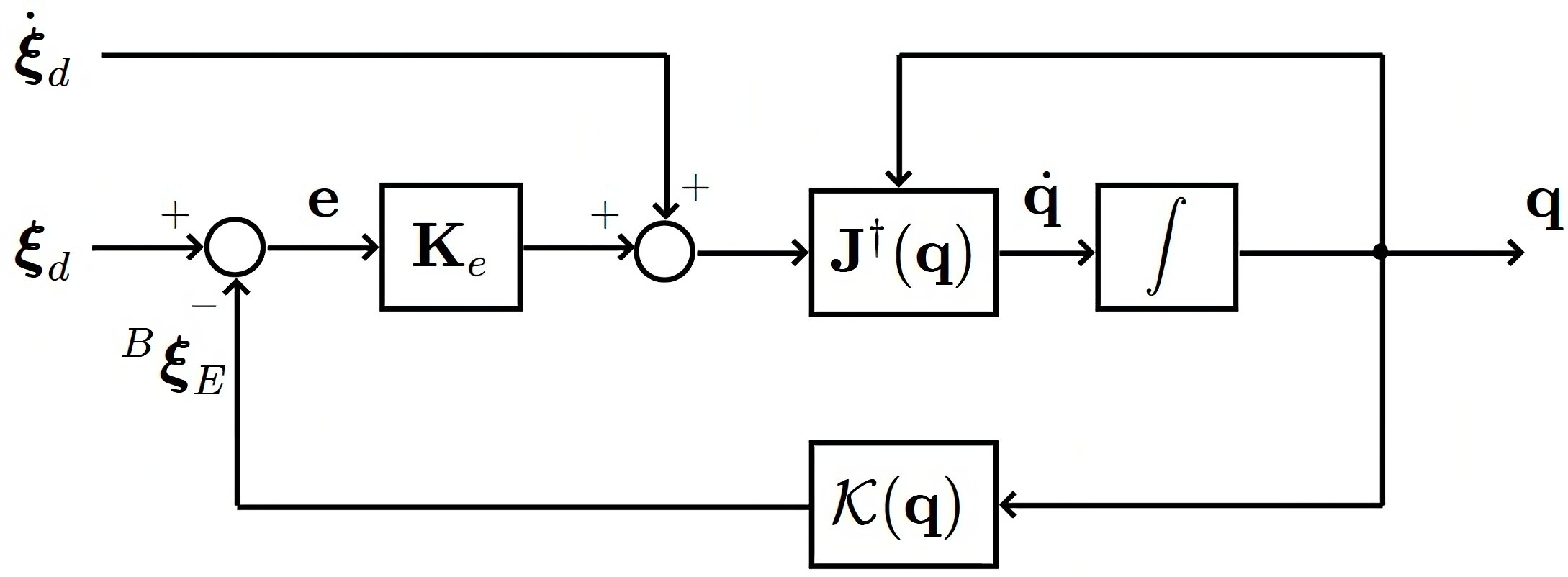
recordemos uno de los principales resultados del control cinemático de manipuladores
recordemos uno de los principales resultados del control cinemático de manipuladores
"inversa" del Jacobiano
recordemos uno de los principales resultados del control cinemático de manipuladores
pose deseada
"inversa" del Jacobiano
cinemática directa
recordemos uno de los principales resultados del control cinemático de manipuladores
pose deseada
"inversa" del Jacobiano
cinemática directa
¿Cuál es el problema con esto?

no es realmente un sensor

¿Qué podemos hacer al respecto?
Control basado en visión
(visual servoing)

cámara + visión por computadora
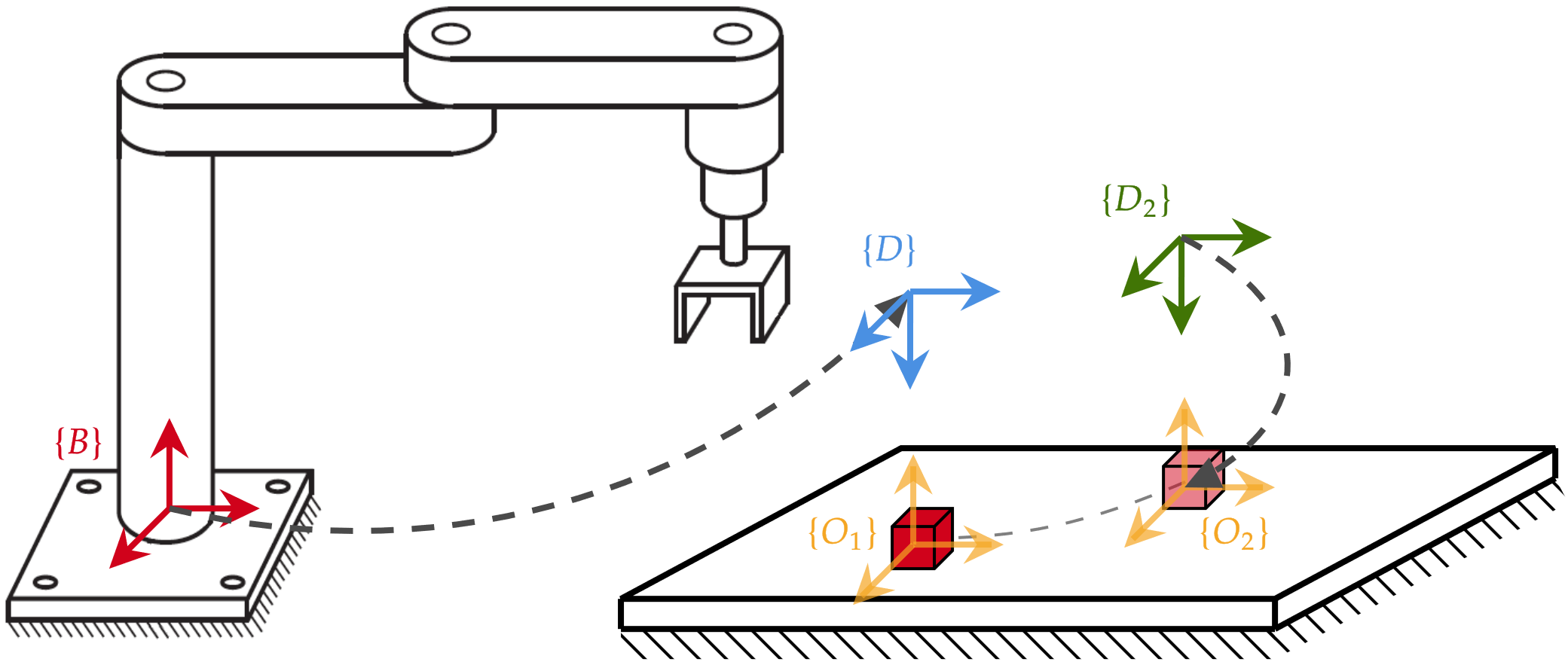
Visual servoing basado en posiciones (PBVS)
- planta = robot, sensor = cámara
- problema de control en el espacio de tarea (3D)
Visual servoing basado en imágenes (IBVS)
- planta = robot + cámara
- problema de control en el plano de imagen (2D)
Position Based Visual Servoing (PBVS)
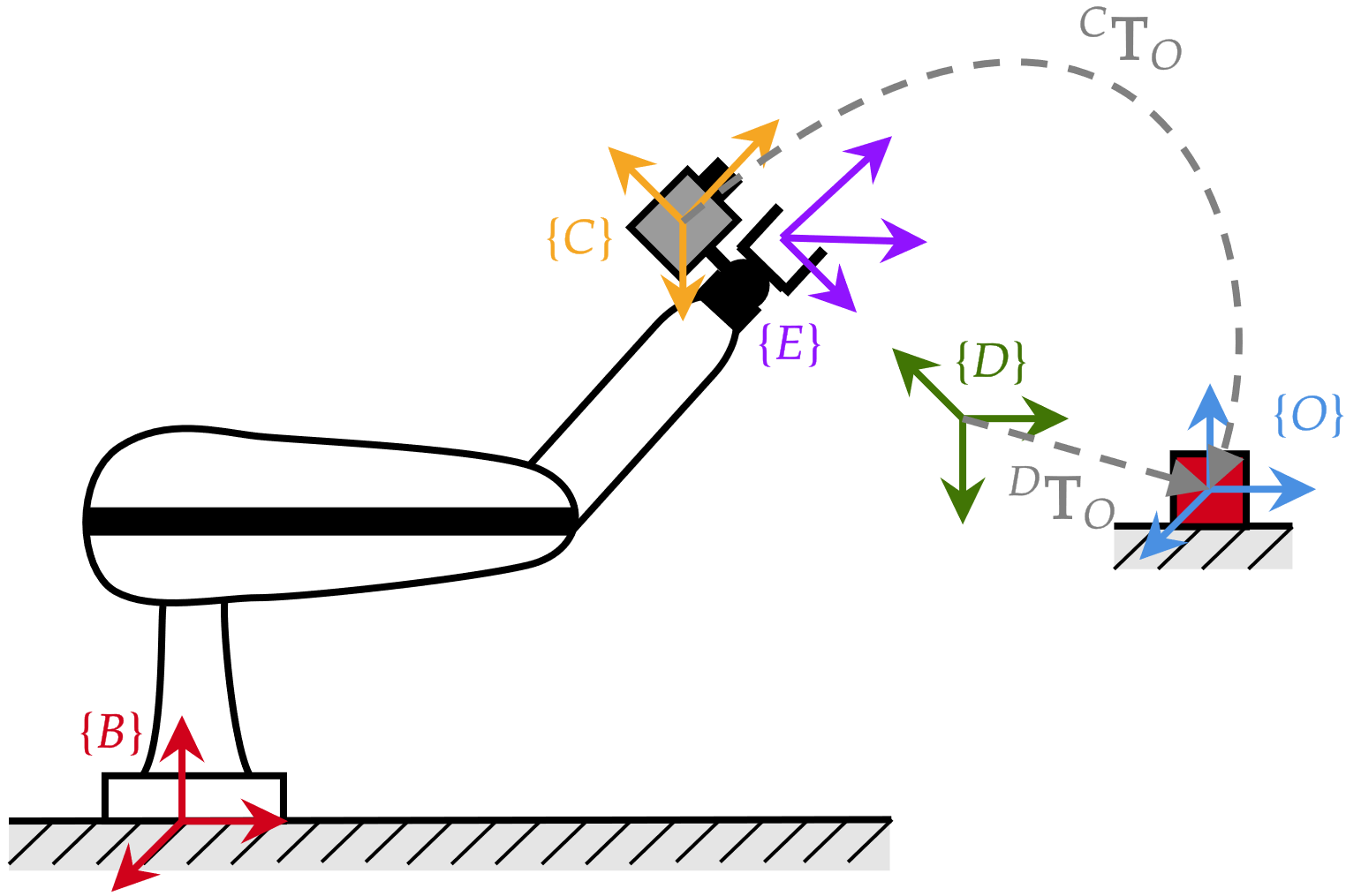
Position Based Visual Servoing (PBVS)

pose deseada del efector final \(\mathbf{T}_d\)
eye-in-hand
Position Based Visual Servoing (PBVS)

pose deseada del efector final \(\mathbf{T}_d\)
objetivo
sin usar poses absolutas
eye-in-hand


...cinemática inversa!
estimación de pose
\({^B}\mathbf{J}\left(\mathbf{q}_k\right)\) Jacobiano "normal"
asume \(\{C\}=\{E\}\)
\({^B}\mathbf{J}\left(\mathbf{q}_k\right)\) Jacobiano "normal"
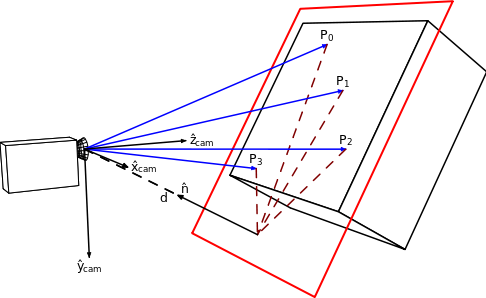
Estimación de pose


Ejemplo: estimación de pose con homografía

>> mt3006_clase4_estimacion_pose.m
P4P con DLT
Una idea más simple: (fiducial) markers


Image Based Visual Servoing (IBVS)

Image Based Visual Servoing (IBVS)

plano de imagen
feature vector
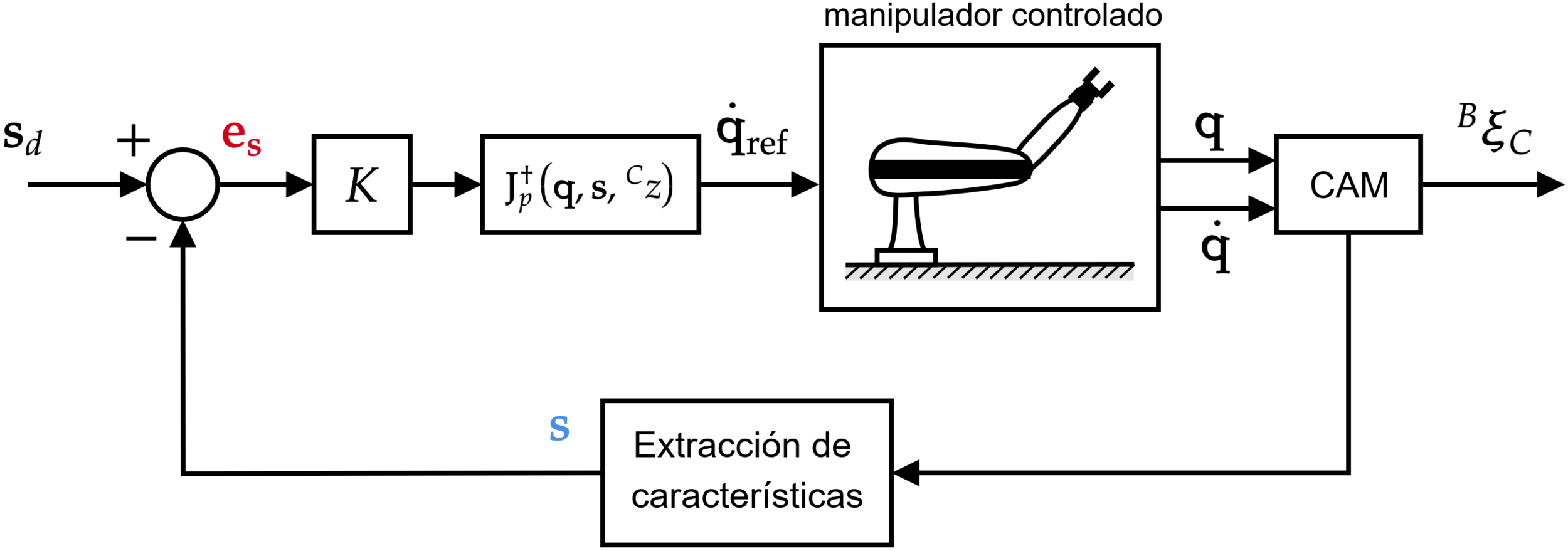

...cinemática inversa otra vez!

>> mt3006_clase4_ibvs_manipulador.m
(asume \(\mathbf{s}_d\) constante)
(asume \(\mathbf{s}_d\) constante)
?
asume \(\{C\}=\{E\}\)
matriz de interacción (depende del tipo de feature)
Feature = punto
Feature = línea
Feature = línea
entre otras, puede revisarse el libro de Corke para ejemplos de más features
Múltiples features
Ejemplo: \(N\) puntos
Múltiples features
Ejemplo: \(N\) puntos
para múltiples features se apilan las matrices de interacción individuales
¿Qué ocurre con los robots móviles con ruedas?
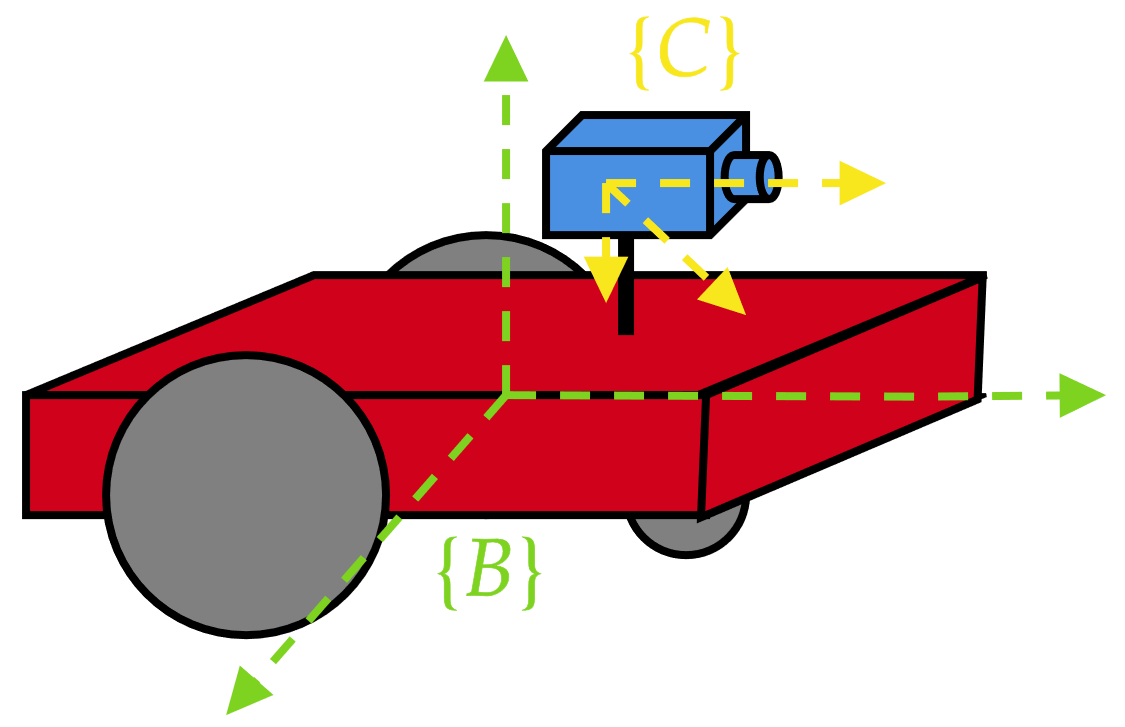
\({^B}\mathbf{v}_B\ne\mathbf{0}\) pero se tiene la ventaja que \({^B}\mathbf{T}_C\) no cambia
Position Based Visual Servoing (PBVS)
objetivo
Position Based Visual Servoing (PBVS)
objetivo
\(\psi_d\) si se tiene control de pose
Position Based Visual Servoing (PBVS)
la estimación de pose se hace una única vez si \(\{O\}\) está fijo
objetivo
Image Based Visual Servoing (IBVS)
Puede extraerse la dinámica en el plano de imagen desde la matriz de interacción ya que el robot móvil sí puede cambiar directamente sus velocidades
Ejemplo: feature = punto
Image Based Visual Servoing (IBVS)
Puede extraerse la dinámica en el plano de imagen desde la matriz de interacción ya que el robot móvil sí puede cambiar directamente sus velocidades
Image Based Visual Servoing (IBVS)
¿Por qué se seleccionaron esas velocidades?
Image Based Visual Servoing (IBVS)
¿Por qué se seleccionaron esas velocidades?
cuidado con la notación, ya que se está empleando \(v\) tanto para la coordenada vertical como para la velocidad lineal
Image Based Visual Servoing (IBVS)
¿Por qué se seleccionaron esas velocidades?
(por ejemplo)
El único problema al emplear IBVS es que se requiere \({^C}z\), el cual se pierde en el mapeo de la cámara. ¿Qué puede hacerse?
- Asumir un valor cte. para la profundidad.
- Añadir un sensor de distancia.
- Estimar la profundidad mediante mínimos cuadrados (libro de Corke).
Aunque en muchos casos pueden no sólo diseñarse controladores sin conocer los parámetros de la cámara y la profundidad, sino también desacoplar la dinámica de los ejes en el plano de imagen
Ejemplo: "encarando" a un punto
se quiere
\(u\to u_0 \equiv \bar{u}\to 0\)
*cuidado con la notación
Ejemplo: "encarando" a un punto
>> mt3006_clase4_ibvs_robotmovil.m
Esta forma de trabajar IBVS con robots móviles puede extrapolarse fácilmente a casos más complicados como UAVs o UUVs siempre que la dimensión del vector de features sea mayor o igual al número de velocidades que pueden controlarse
Referencias
- P. Corke, Robotics Vision and Control Fundamental Algorithms in MATLAB, capítulos 15 y 16.
- B. Siciliano, Robotics: Modelling, Planning and Control, capítulo 10.