El perceptrón y redes neuronales

(no profundas)

MT3006 - Robótica 2

El perceptrón como bloque fundamental

¿Cómo?

entradas

pesos

suma

\displaystyle \hat{y}=g\left(\sum_{j=1}^{d} w_jx_j+w_0\right)=g\left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)
\tilde{\mathbf{x}}=\begin{bmatrix} 1 \\ \mathbf{x} \end{bmatrix}=\begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}

entradas

pesos

suma

\displaystyle \hat{y}=g\left(\sum_{j=1}^{d} w_jx_j+w_0\right)=g\left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)
\tilde{\mathbf{x}}=\begin{bmatrix} 1 \\ \mathbf{x} \end{bmatrix}=\begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}

término de bias

entradas

pesos

suma

\displaystyle \hat{y}=g\left(\sum_{j=1}^{d} w_jx_j+w_0\right)=g\left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)
\tilde{\mathbf{x}}=\begin{bmatrix} 1 \\ \mathbf{x} \end{bmatrix}=\begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}

término de bias

pensemos sobre realmente qué es esto y cuáles son sus limitantes

entradas

pesos

suma

función de activación

(no linealidad)

\displaystyle \hat{y}=g\left(\sum_{j=1}^{d} w_jx_j+w_0\right)=g\left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)
\tilde{\mathbf{x}}=\begin{bmatrix} 1 \\ \mathbf{x} \end{bmatrix}=\begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}

entradas

pesos

suma

salida

\displaystyle \hat{y}=g\left(\sum_{j=1}^{d} w_jx_j+w_0\right)=g\left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)
\tilde{\mathbf{x}}=\begin{bmatrix} 1 \\ \mathbf{x} \end{bmatrix}=\begin{bmatrix} 1 \\ x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}

hipótesis

función de activación

(no linealidad)

Funciones de activación "comunes"

Funciones de activación "comunes"

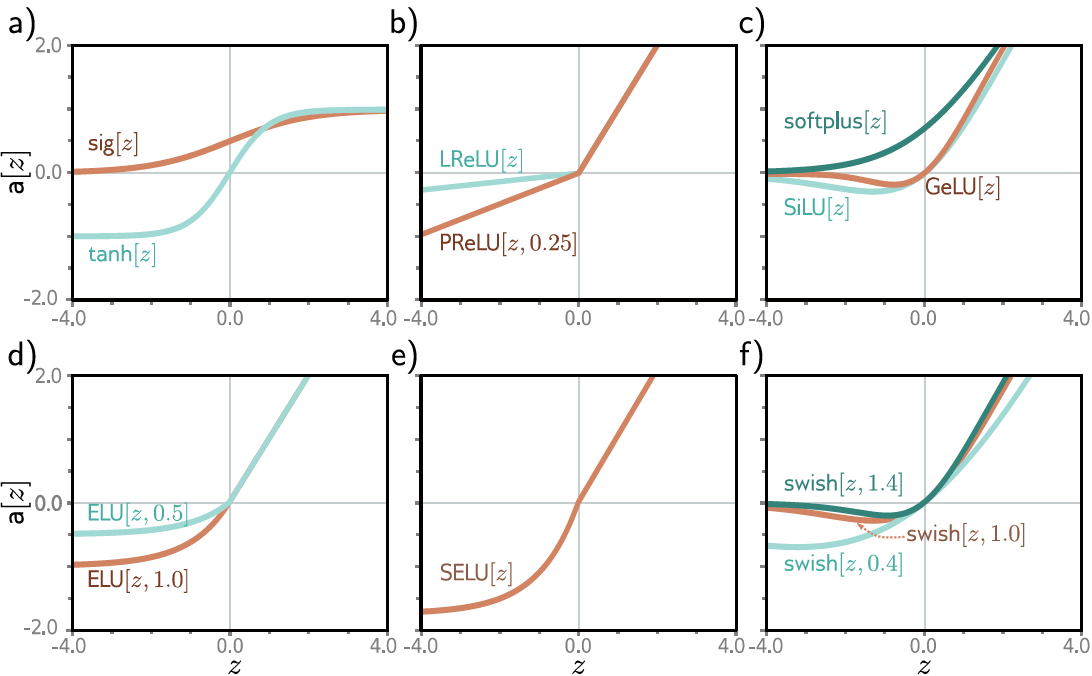
el perceptrón original empleaba el escalón unitario

\hat{y}=f\left(\mathbf{x},\mathbf{w}\right)=\mathbf{1} \left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)=\begin{cases} 1 & \text{ si } \mathbf{w}^\top \tilde{\mathbf{x}}\ge0 \\ 0 & \text{ si } \mathbf{w}^\top \tilde{\mathbf{x}}<0 \end{cases}

el perceptrón original empleaba el escalón unitario

\hat{y}=f\left(\mathbf{x},\mathbf{w}\right)=\mathbf{1} \left(\mathbf{w}^\top \tilde{\mathbf{x}}\right)=\begin{cases} 1 & \text{ si } \mathbf{w}^\top \tilde{\mathbf{x}}\ge0 \\ 0 & \text{ si } \mathbf{w}^\top \tilde{\mathbf{x}}<0 \end{cases}

mapa lineal \(\equiv\) hiperplano en \(\mathbb{R}^d\)

la función de activación introduce la no linealidad que hace posible la clasificación binaria

Ejemplo

\displaystyle L(\mathbf{w})=\dfrac{1}{2} \sum_{i=1}^{n} \left[y^{(i)}-f(\mathbf{x}^{(i)},\mathbf{w})\right]^2

>> mt3006_clase6_perceptron.m

función de activación sigmoide

\(f=\sigma\)

Ejemplo

\displaystyle \mathbf{w}^\star=\begin{bmatrix} w_0^\star \\ w_1^\star \\ w_2^\star \end{bmatrix}=\arg\min_{\mathbf{w}} L(\mathbf{w})

hiperplano separador

=\begin{bmatrix} -3.8383 \\ 2.0384 \\ 2.0087\end{bmatrix}
x_2=mx_1+b=-\dfrac{w_1^\star}{w_2^\star}x_1-\dfrac{w_0^\star}{w_2^\star}

Ejemplo

\displaystyle \mathbf{w}^\star=\begin{bmatrix} w_0^\star \\ w_1^\star \\ w_2^\star \end{bmatrix}=\arg\min_{\mathbf{w}} L(\mathbf{w})

hiperplano separador

=\begin{bmatrix} -3.8383 \\ 2.0384 \\ 2.0087\end{bmatrix}
x_2=mx_1+b=-\dfrac{w_1^\star}{w_2^\star}x_1-\dfrac{w_0^\star}{w_2^\star}

¿Cuándo falla el perceptrón?

Ejemplo: XOR

A B A XOR B
0 0 0
0 1 1
1 0 1
1 1 0

A

B

0

1

1

Ejemplo: XOR

A B A XOR B
0 0 0
0 1 1
1 0 1
1 1 0

A

B

0

1

1

La data no es linealmente separable

Ejemplo: XOR

A B A XOR B
0 0 0
0 1 1
1 0 1
1 1 0

A

B

0

1

1

La data no es linealmente separable

?

¿Solución?

\equiv
z=\mathbf{w}^\top\tilde{\mathbf{x}}

¿Solución?

z=\mathbf{w}^\top\tilde{\mathbf{x}}
g(\cdot)

¿Solución?

¿Solución?

dense layer

\displaystyle z_m=g\left( \sum_{j=1}^{d} w_{j,m} x_j+w_{0,m} \right)=g\left( \mathbf{w}_m^\top\tilde{\mathbf{x}} \right)
\mathbf{w}_m=\begin{bmatrix} w_{0,m} \\ w_{1,m} \\ \vdots \\ w_{d,m} \end{bmatrix}
\mathbf{W}=\begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 \end{bmatrix}

¿Solución?

\cdots
\cdots

Red neuronal (de una capa)

\cdots
\cdots
\displaystyle z_m=g\left(\sum_{j=1}^{d} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right) \\ =g\left(\mathbf{w}^{(1)\top}_m \tilde{\mathbf{x}}\right)

entradas

salidas

capa oculta

\tilde{\mathbf{z}}=\begin{bmatrix} 1 \\ \mathbf{z} \end{bmatrix}=\begin{bmatrix} 1 \\ g\left(\mathbf{w}^{(1)\top}_1 \tilde{\mathbf{x}}\right) \\ \vdots \\ g\left(\mathbf{w}^{(1)\top}_{M_1} \tilde{\mathbf{x}}\right) \end{bmatrix}
\displaystyle z_m=g\left(\sum_{j=1}^{d} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right) \\ =g\left(\mathbf{w}^{(1)\top}_m \tilde{\mathbf{x}}\right)

entradas

salidas

capa oculta

\displaystyle \hat{y}_k=g\left(\sum_{m=1}^{M_1} w_{m,k}^{(2)} z_m+w_{0,k}^{(2)}\right)\\ =g\left(\mathbf{w}_k^{(2)\top}\tilde{\mathbf{z}}\right)
\displaystyle z_m=g\left(\sum_{j=1}^{d} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right) \\ =g\left(\mathbf{w}^{(1)\top}_m \tilde{\mathbf{x}}\right)

entradas

salidas

capa oculta

\displaystyle \hat{y}_k=g\left(\sum_{m=1}^{M_1} w_{m,k}^{(2)} z_m+w_{0,k}^{(2)}\right)\\ =g\left(\mathbf{w}_k^{(2)\top}\tilde{\mathbf{z}}\right)

¿Por qué?

El teorema de aproximación universal

Establece que una red neuronal de una sola capa, también conocido como perceptrón multicapa (MLP), con una función de activación no lineal adecuada, puede aproximar cualquier función continua definida en un espacio compacto con una precisión arbitraria, siempre y cuando se le permita tener un número suficiente de neuronas en la capa oculta.

- ChatGPT 4o

Una justificación retroactiva

Una justificación retroactiva

Una justificación retroactiva

a)

b)

c)

Una justificación retroactiva

d)

e)

f)

Una justificación retroactiva

g)

h)

i)

Una justificación retroactiva

j)

Una justificación retroactiva

j)

otros posibles modelos con parámetros distintos

Una justificación retroactiva

¿Qué ocurre conforme se añaden nodos a la capa oculta?

Entrenando la red neuronal

Algunos problemas prácticos

A pesar que se tiene un fundamento teórico del porqué las redes neuronales deberían de funcionar, aún falta encontrar el cómo resolver los problemas prácticos de su implementación.

Principalmente, cómo resolver de manera práctica el problema de optimización.

Un ejemplo de impracticidad

red neuronal de una capa

dataset MNIST

28x28 pixeles = 784 + 1 features

800 nodos \(\Rightarrow\) 801 "features"

10 categorías

\mathbf{W}^\star=\displaystyle \argmin_{\mathbf{W}} \sum_{i=1}^{n} \sum_{k=1}^{10} \left[y_k^{(i)}-g\left(\sum_{m=1}^{800} w_{m,k}^{(2)} g\left(\sum_{j=1}^{784} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right)+w_{0,k}^{(2)}\right)\right]^2
\mathbf{W}^\star=\displaystyle \argmin_{\mathbf{W}} \sum_{i=1}^{n} \sum_{k=1}^{10} \left[y_k^{(i)}-g\left(\sum_{m=1}^{800} w_{m,k}^{(2)} g\left(\sum_{j=1}^{784} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right)+w_{0,k}^{(2)}\right)\right]^2

pérdida de error cuadrático

636010 variables de decisión

\mathbf{W}^\star=\displaystyle \argmin_{\mathbf{W}} \sum_{i=1}^{n} \sum_{k=1}^{10} \left[y_k^{(i)}-g\left(\sum_{m=1}^{800} w_{m,k}^{(2)} g\left(\sum_{j=1}^{784} w_{j,m}^{(1)} x_j+w_{0,m}^{(1)}\right)+w_{0,k}^{(2)}\right)\right]^2

pérdida de error cuadrático

636010 variables de decisión

problema de optimización (no) convexo de escala masiva

*aunque con la ventaja que no presenta restricciones

Resolviendo estos problemas

Gradient descent

\mathbf{x}_{r+1}=\mathbf{x}_r-\alpha_r\nabla f\left(\mathbf{x}_r\right)
\mathbf{x}^\star=\displaystyle \argmin_{\mathbf{x}} f(\mathbf{x})
\displaystyle \lim_{r\to\infty} \mathbf{x}_r=\mathbf{x}^\star

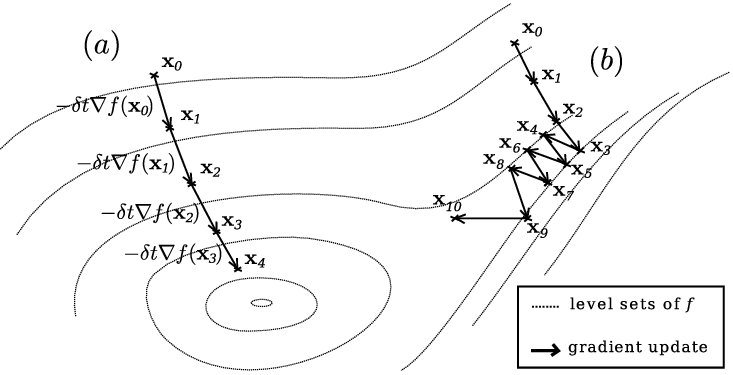
Una forma de resolver problemas de optimización no lineales sin restricciones es mediante el método del descenso del gradiente.

Gradient descent

\mathbf{x}_{r+1}=\mathbf{x}_r-\alpha_r\nabla f\left(\mathbf{x}_r\right)
\mathbf{x}^\star=\displaystyle \argmin_{\mathbf{x}} f(\mathbf{x})
\displaystyle \lim_{r\to\infty} \mathbf{x}_r=\mathbf{x}^\star

learning rate

Una forma de resolver problemas de optimización no lineales sin restricciones es mediante el método del descenso del gradiente.

>> mt3006_clase6_gradientdescent.m

Gradient descent

Por el tipo de problema, sin embargo, la solución puede ser sólo un mínimo local.

loss landscape

Aplicando esto al caso de la red neuronal de una capa:

\mathbf{W}_{r+1}=\mathbf{W}_r-\alpha_r\nabla L\left(\mathbf{W}_r\right)
\displaystyle L(\mathbf{w})=\sum_{i=1}^{n} \sum_{k=1}^{K} \ell\left(y_k^{(i)}-f_k(\mathbf{x}^{(i)},\mathbf{w})\right) =\sum_{i=1}^{n} \sum_{k=1}^{K} \ell\left(y_k^{(i)}-g\left(\mathbf{w}_k^{(2)\top}\tilde{\mathbf{z}}^{(i)}\right)\right)
\nabla L(\mathbf{w})=

Aplicando esto al caso de la red neuronal de una capa:

\mathbf{W}_{r+1}=\mathbf{W}_r-\alpha_r\nabla L\left(\mathbf{W}_r\right)
\displaystyle L(\mathbf{w})=\sum_{i=1}^{n} \sum_{k=1}^{K} \ell\left(y_k^{(i)}-f_k(\mathbf{x}^{(i)},\mathbf{w})\right) =\sum_{i=1}^{n} \sum_{k=1}^{K} \ell\left(y_k^{(i)}-g\left(\mathbf{w}_k^{(2)\top}\tilde{\mathbf{z}}^{(i)}\right)\right)
\nabla L(\mathbf{w})=

???

demasiado complicado

Consideremos un caso más simple como ejemplo (misma función de activación con pérdida cuadrática):

\hat{y}
z
x_1
x_2
L(\mathbf{w})=\dfrac{1}{2}\sum_{i=1}^{n}\left[y^{(i)}-g\left(w_2^{(2)}z_0^{(i)}+w_1^{(2)}g\left(w_0^{(1)}x_0^{(i)}+w_1^{(1)}x_1^{(i)}+w_2^{(1)}x_2^{(i)}\right)\right)\right]^2
z_1^{(i)}=g\left(w_0^{(1)}x_0^{(i)}+w_1^{(1)}x_1^{(i)}+w_2^{(1)}x_2^{(i)}\right)
\hat{y}^{(i)}=g\left(w_0^{(2)}z_0^{(i)}+w_1^{(2)}z_1^{(i)}\right)
x_0^{(i)}=z_0^{(i)}=1

Consideremos un caso más simple como ejemplo (misma función de activación con pérdida cuadrática):

\hat{y}
z
x_1
x_2
z_1^{(i)}=g\left(w_0^{(1)}x_0^{(i)}+w_1^{(1)}x_1^{(i)}+w_2^{(1)}x_2^{(i)}\right)
\hat{y}^{(i)}=g\left(w_0^{(2)}z_0^{(i)}+w_1^{(2)}z_1^{(i)}\right)
\dfrac{\partial L(\mathbf{w})}{\partial w_j^{(2)}}= -\sum_{i=1}^{n}\left(y^{(i)}-\hat{y}^{(i)}\right)g'\left(w_0^{(2)}z_0^{(i)}+w_1^{(2)}z_1^{(i)}\right)z_j^{(i)} =-\sum_{i=1}^{n} \delta^{(i)} z_j^{(i)}
x_0^{(i)}=z_0^{(i)}=1

Consideremos un caso más simple como ejemplo (misma función de activación con pérdida cuadrática):

\hat{y}
z
x_1
x_2
z_1^{(i)}=g\left(w_0^{(1)}x_0^{(i)}+w_1^{(1)}x_1^{(i)}+w_2^{(1)}x_2^{(i)}\right)
\hat{y}^{(i)}=g\left(w_0^{(2)}z_0^{(i)}+w_1^{(2)}z_1^{(i)}\right)
\dfrac{\partial L(\mathbf{w})}{\partial w_j^{(1)}}= -\sum_{i=1}^{n}\left(y^{(i)}-\hat{y}^{(i)}\right)g'\left(w_0^{(2)}z_0^{(i)}+w_1^{(2)}z_1^{(i)}\right) \cdots \\ \cdots w_j^{(2)}g'\left(w_0^{(1)}x_0^{(i)}+w_1^{(1)}x_1^{(i)}+w_2^{(1)}x_2^{(i)}\right) x_j^{(i)} =-\sum_{i=1}^{n} s\left(\delta^{(i)}, w_j^{(2)} \right) x_j^{(i)}=-\sum_{i=1}^{n} s^{(i)} x_j^{(i)}
x_0^{(i)}=z_0^{(i)}=1

Por lo tanto

w_j^{(2)}[r+1]=w_j^{(2)}[r]+\alpha\sum_{i=1}^{n} \delta^{(i)} z_j^{(i)}
w_j^{(1)}[r+1]=w_j^{(1)}[r]+\alpha\sum_{i=1}^{n} s^{(i)} x_j^{(i)}

Por lo tanto

w_j^{(2)}[r+1]=w_j^{(2)}[r]+\alpha\sum_{i=1}^{n} \delta^{(i)} z_j^{(i)}
w_j^{(1)}[r+1]=w_j^{(1)}[r]+\alpha\sum_{i=1}^{n} s^{(i)} x_j^{(i)}

Adicionalmente, ¿Qué ocurre si en lugar del set completo de entrenamiento sólo seleccionamos un ejemplo (aleatorio)? \(\Rightarrow\) Stochastic Gradient Descent (SGD)

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}
z^{(i)}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}
z^{(i)}
\hat{y}^{(i)}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r
\mathbf{W}_r

forward propagation

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}
z^{(i)}
\hat{y}^{(i)}
\delta^{(i)}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r
\mathbf{W}_r

forward propagation

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}
z^{(i)}
\hat{y}^{(i)}
\delta^{(i)}
s^{(i)}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r
\mathbf{W}_r

forward propagation

\mathbf{W}_{r+1}

Estas fórmulas esconden un algoritmo altamente eficiente para la actualización de parámetros

\hat{y}
z
x_1
x_2
\mathbf{x}^{(i)}
z^{(i)}
\hat{y}^{(i)}
\delta^{(i)}
s^{(i)}
\mathbf{W}_{r+1}

\(i-\)ésimo ejemplo (aleatorio)

\mathbf{W}_r
\mathbf{W}_r

forward propagation

back propagation

\mathbf{W}_{r+1}
  1. Más allá de ser un "hack", el SGD hace que la trayectoria de los parámetros óptimos evite mínimos locales.
  2. El entrenar ejemplo-por-ejemplo permite entrenar a la red neuronal de forma online.

  3. A pesar de haber encontrado fórmulas, esto es igualmente complicado. ¿Qué hacemos para más capas, o para arquitecturas más complejas?

Algunas consideraciones

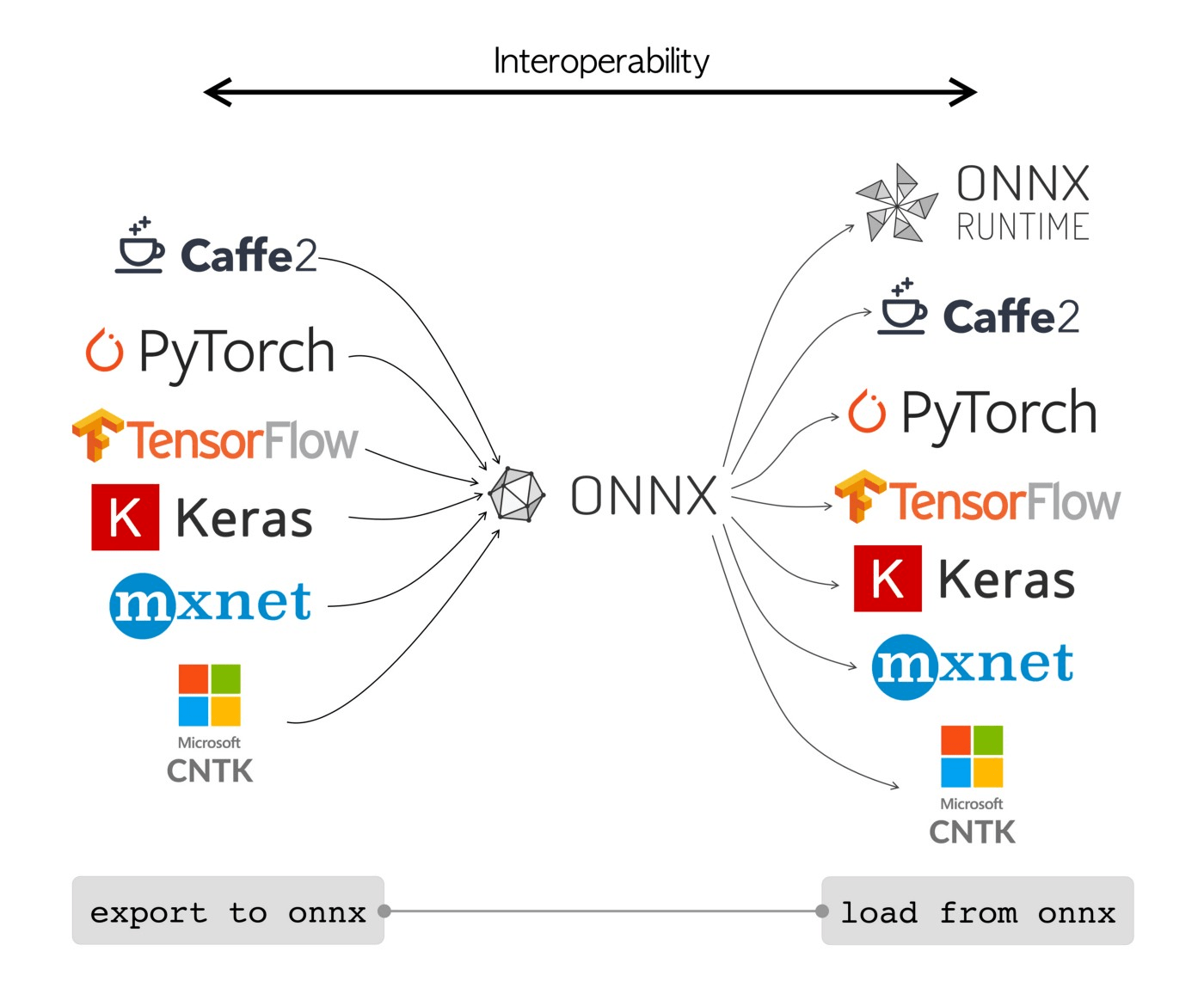
Frameworks para deep learning

fáciles, útiles para prototipado

más populares para implementación

Referencias

  1. S. Prince, Understanding Deep Learning, capítulo 3.
import tensorflow as tf
from tf.keras import Sequential
from tf.keras.layers import Dense

# Se define el modelo
hidden_layer = Dense(M1, activation = 'sigmoid')
output_layer = Dense(2, activation = 'relu')
model = Sequential([hidden_layer, output_layer])

# O bien:
model = Sequential()
model.add(hidden_layer)
model.add(output_layer)

# Se compila y entrena el modelo
model.compile(loss = 'mean_squared_error', optimizer = 'SGD')
model.fit(trainSet, trainLabels, epochs = 100)