Redes neuronales convolucionales

MT3006 - Robótica 2

¿Por qué?

De MLPs a redes especializadas
Supongamos que se tiene una aplicación en donde deben clasificarse imágenes a color en dos categorías
De MLPs a redes especializadas
¿Cuáles deberían ser las especificaciones típicas de una red neuronal para esto, formada por perceptrones?
¿Dimensión de cada ejemplo? (asumiendo que se emplean las imágenes en bruto)
\(\dim(\mathbf{x})=224 \times 224 \times 3=150528\)
¿Nodos por capa? Típicamente, las redes que funcionan contienen más nodos que entradas
\(\left(D \ge \dim(\mathbf{x})\right) \times K\) capas \(\sim D^K\)
Inclusive en el caso mínimo de una única capa oculta, esto implica una cantidad impráctica de parámetros
\(\dim(\mathbf{W}) \sim 150528(150529) + 150529\approx 23\) billones
Inclusive en el caso mínimo de una única capa oculta, esto implica una cantidad impráctica de parámetros
\(\dim(\mathbf{W}) \sim 150528(150529) + 150529\approx 23\) billones
A parte de ser un modelo innecesariamente gigante, también conlleva otras implicaciones:
- Un rule of thumb establece \(\approx 10\times\) la cantidad de parámetros del modelo, es decir \(\approx\) un cuarto de trillón.
- De manera más conservadora, si se quisiera muestrear con una densidad del 1% del rango permisible por pixel se requerirían \(\approx 3\) ejemplos por dimensión de entrada, es decir \(3^{150528}\) que es mayor al número de partículas en el universo (\(3.28\times 10^{80}\)). Esto se conoce como el curse of dimensionality.
Número requerido de ejemplos
- Para imágenes (interpretables por humanos) sabemos que los pixeles cercanos se encuentran estadísticamente relacionados. Sin embargo, la red con perceptrones no considera esto y trata a cada pixel como independiente (y forma relaciones densas entre los mismos y las neuronas).
- Las imágenes presentan ciertas simetrías particulares, como invarianza y equivarianza, que hacen que, por ejemplo, un árbol sea un árbol sin importar su orientación o escala.
Particularidades de la data a procesar
Invarianza

perro
Invarianza


perro
Invarianza


perro
perro
Debería dar un flashback a sistemas LTI


perro
perro
Equivarianza


Equivarianza



Equivarianza




Equivarianza




¿Solución?
Capas| redes convolucionales (CNNs)
entrada \(\mathbf{X}\)
(imagen)
pesos \(\mathbf{W}\) (matriz)
salida \(\mathbf{Y}\)
(imagen)
entrada \(\mathbf{X}\)
(imagen)
pesos \(\mathbf{W}\) (matriz) \(\equiv\) kernel
salida \(\mathbf{Y}\)
(imagen)
ReLU
(típicamente)
Recordando algunos detalles sobre la convolución en imágenes

(0)(1) + (-1)(1) + (0)(3)
+ (-1)(1) + (5)(1) + (-1)(3) + (0)(2) + (-1)(2) + (0)(1) = -2
padding
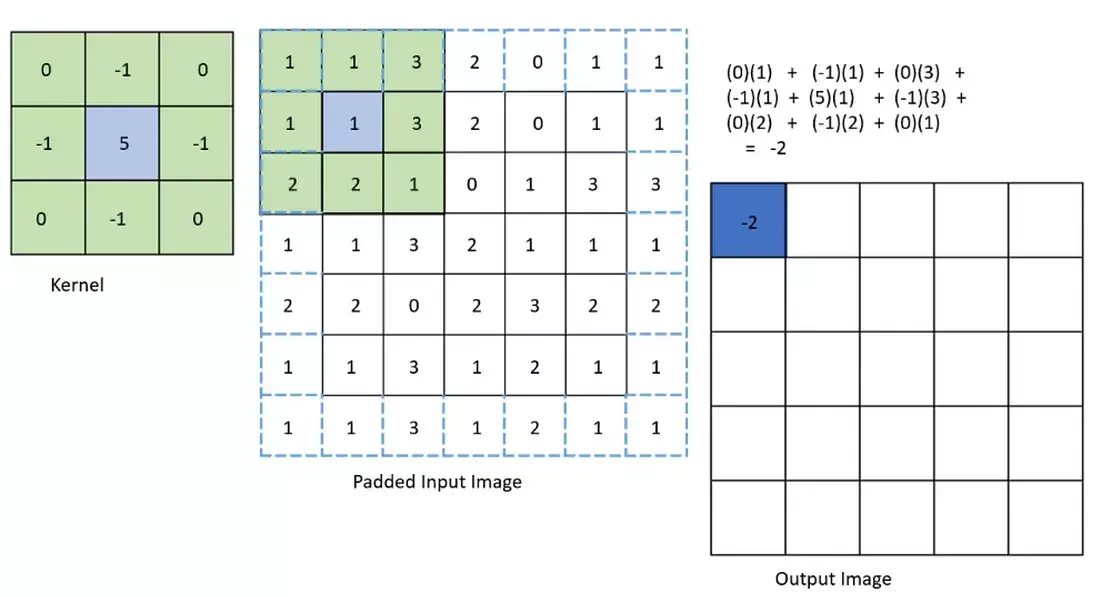
kernel size

salto entre pixeles o stride
El stride reduce la dimensión de la salida
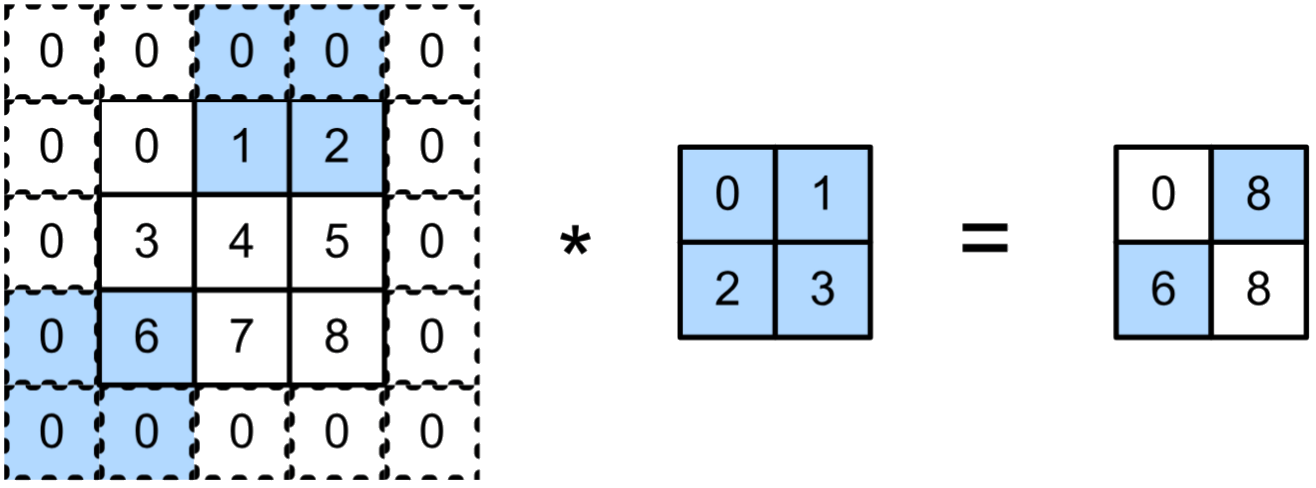
Stride horizontal de 2 y vertical de 3
entrada
kernel
salida
Template matching



Template matching



Regresando a redes convolucionales
¿Ventaja sobre perceptrones?
El explotar las particularidades en imágenes permite conexiones menos densas (o más dispersas) entre nodos. Por ejemplo:
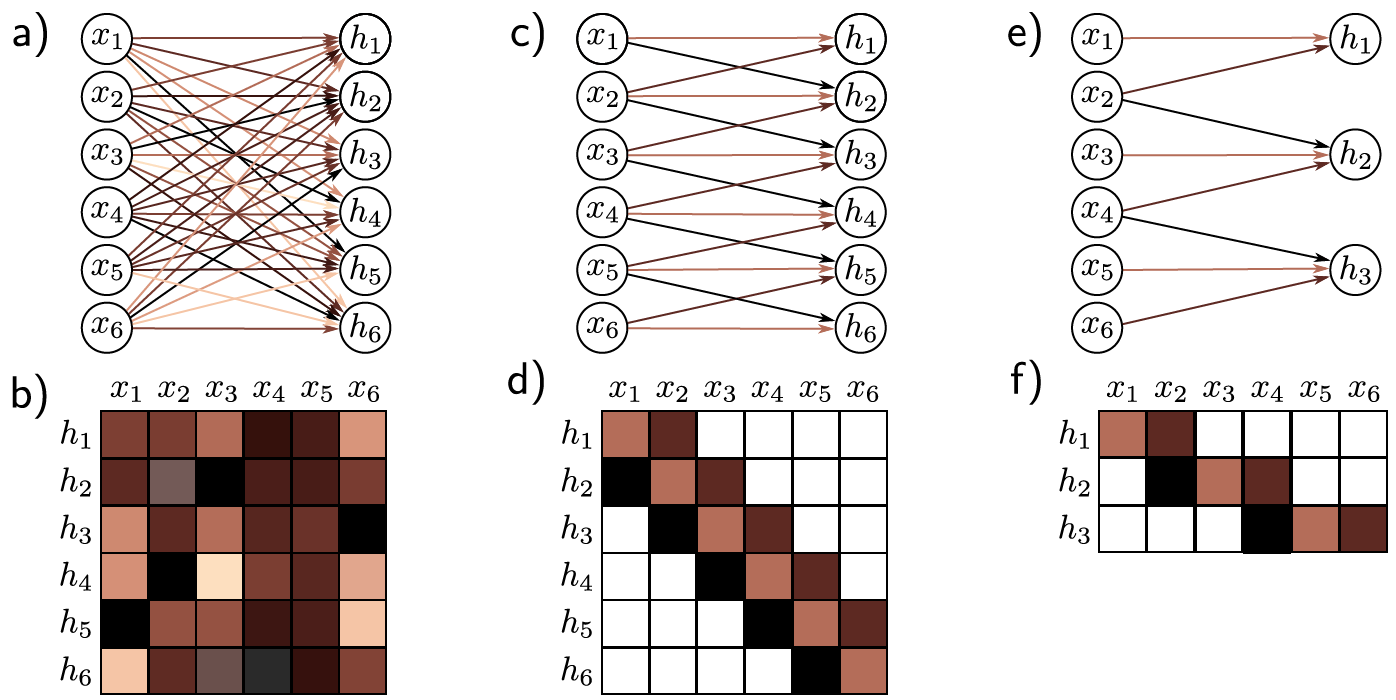
capa convolucional 1D
matriz de pesos
stride = 2
¿Ventaja sobre perceptrones?
El emplear capas | redes especializadas también aporta en qué tanto puede "explicarse" el comportamiento del modelo de aprendizaje.
¿Ventaja sobre perceptrones?
El emplear capas | redes especializadas también aporta en qué tanto puede "explicarse" el comportamiento del modelo de aprendizaje.
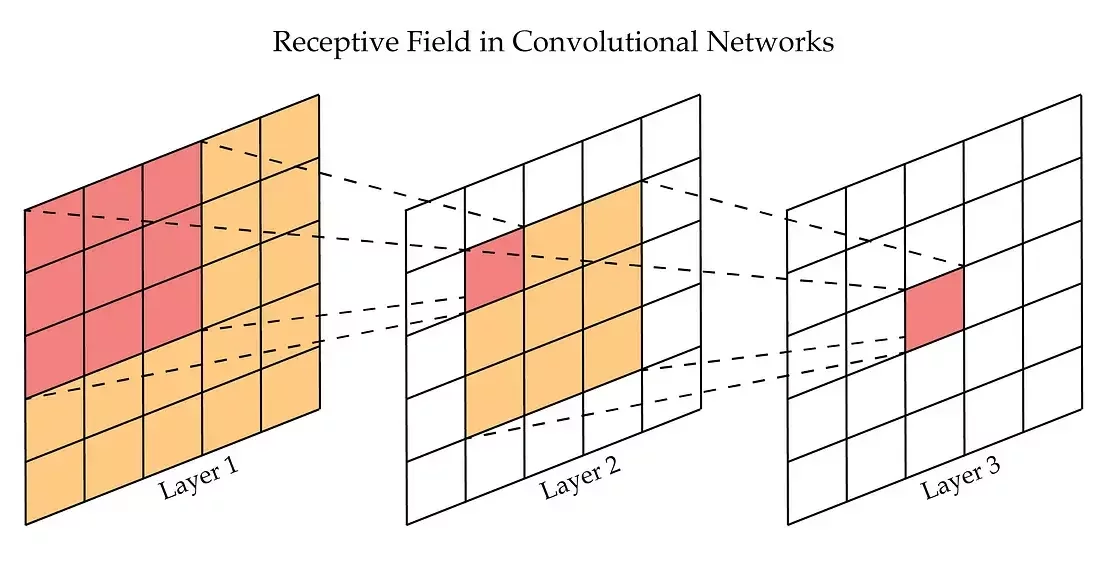
Por ejemplo, las CNNs se asemejan a la manera en que funciona el córtex visual de diversos animales (incluyendo humanos), empleando la noción conocida como campos receptivos (receptive fields).
Feature maps y receptive fields
Puede incrementarse la "apertura" del kernel mediante el parámetro de dilatación (dilation), donde se "incrementa" (artificialmente) su tamaño insertando ceros.
Feature maps y receptive fields
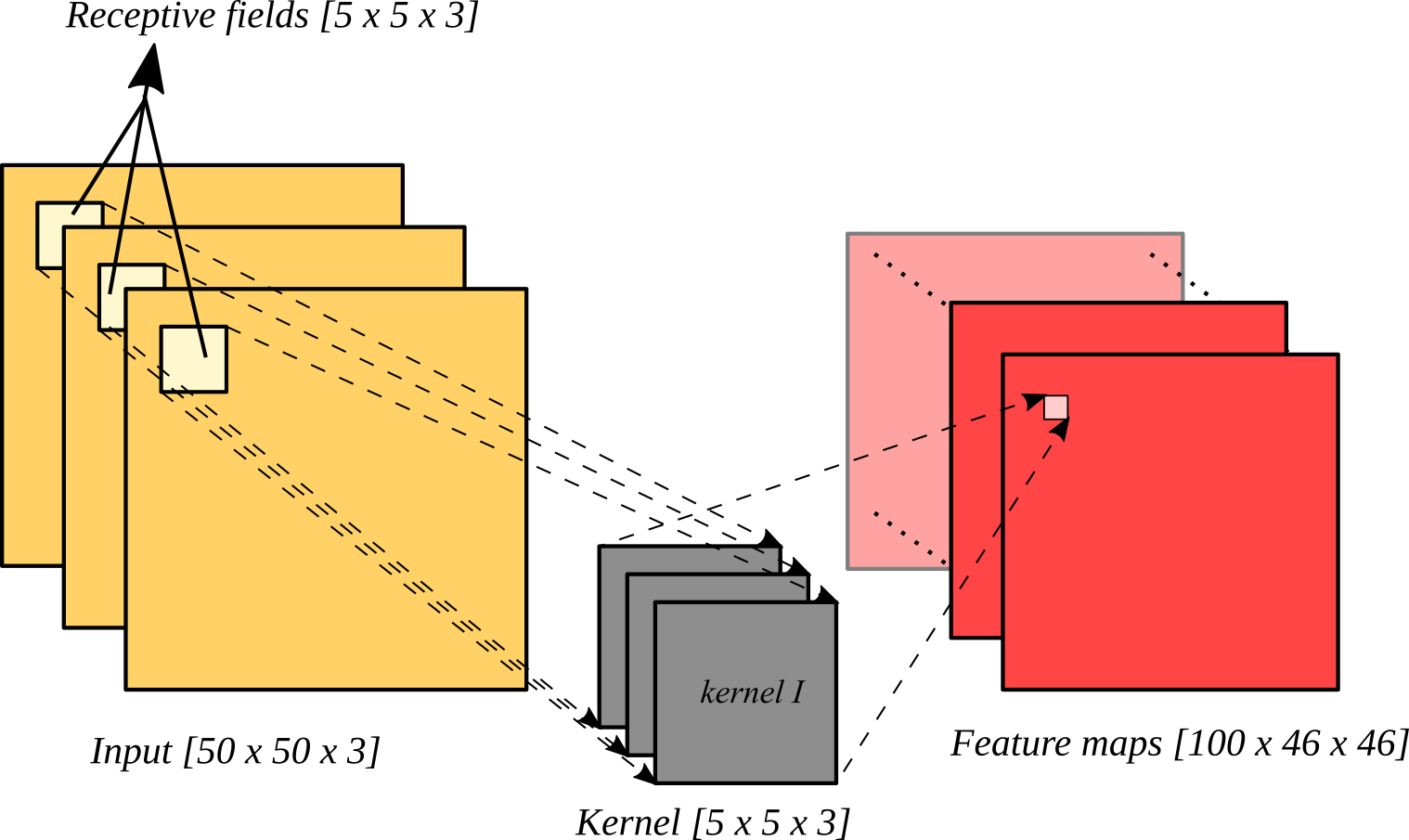
Feature maps y receptive fields
La "primera" CNN influyente
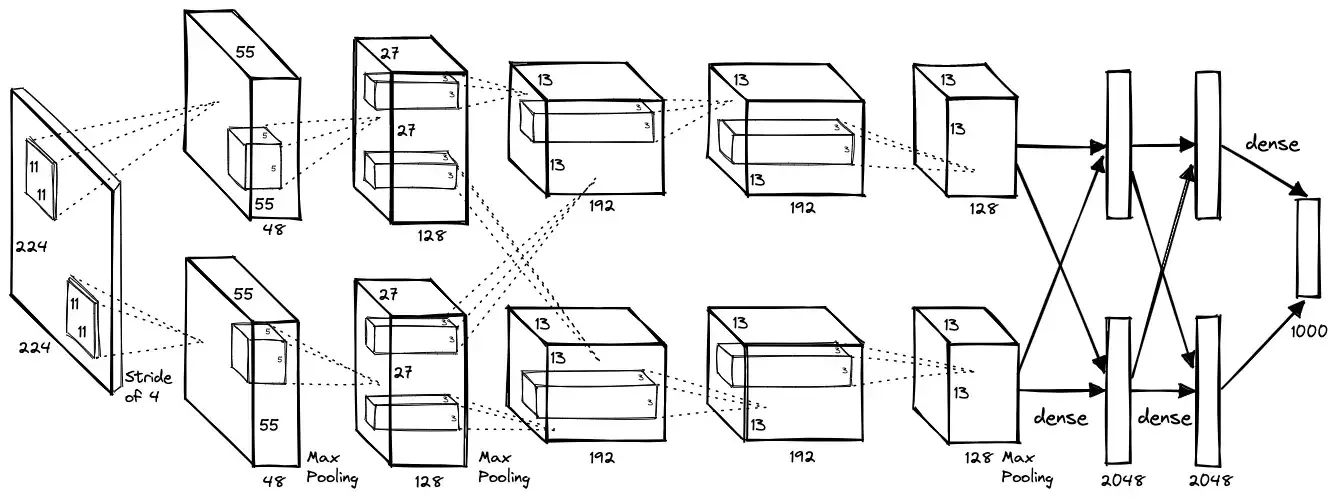
AlexNet gana la ImageNet Challenge en 2012
https://www.image-net.org/challenges/LSVRC/2012/results.html
La "primera" CNN influyente

AlexNet gana la ImageNet Challenge en 2012
https://www.image-net.org/challenges/LSVRC/2012/results.html
Presenta una arquitectura típica para CNNs
Arquitectura prototípica
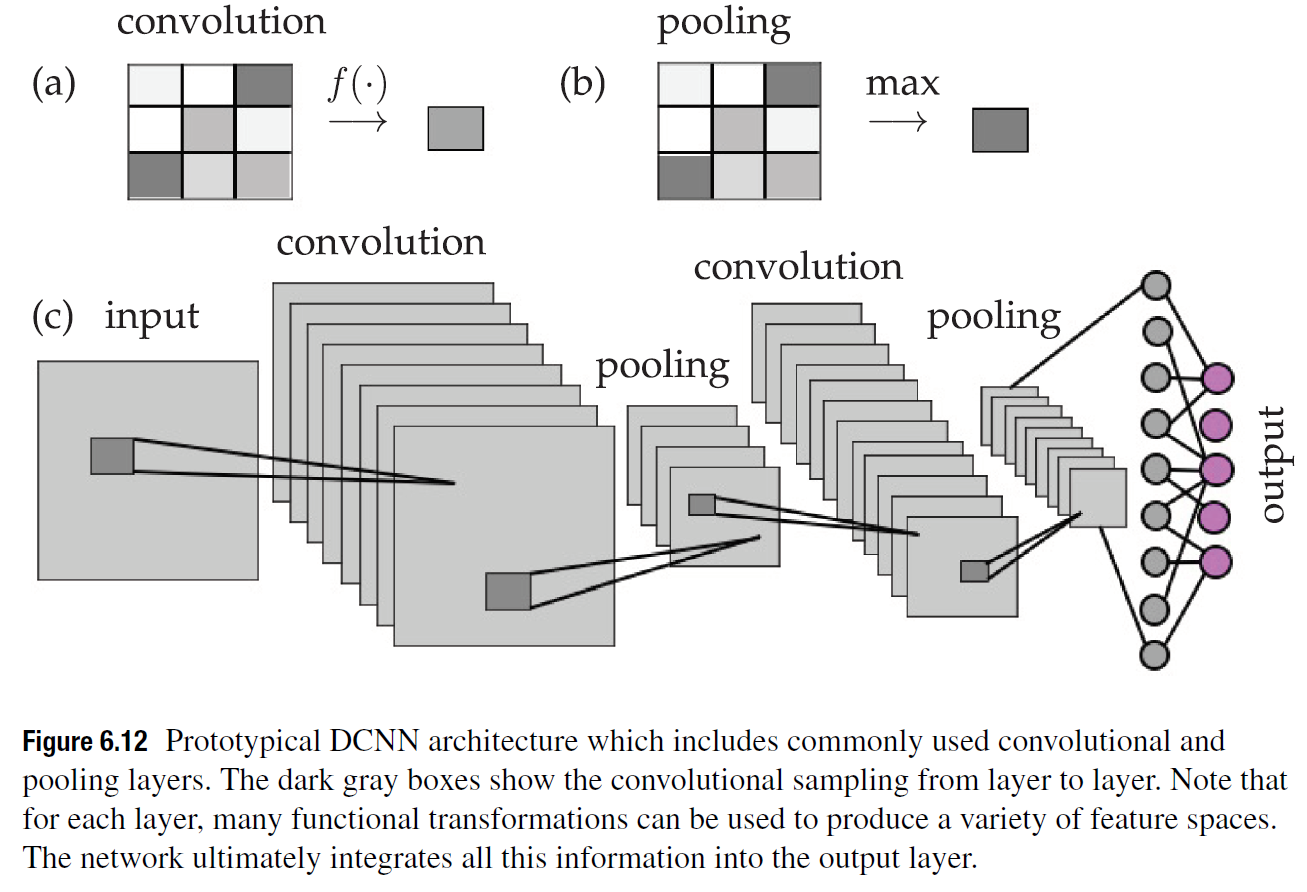
Arquitectura prototípica

???
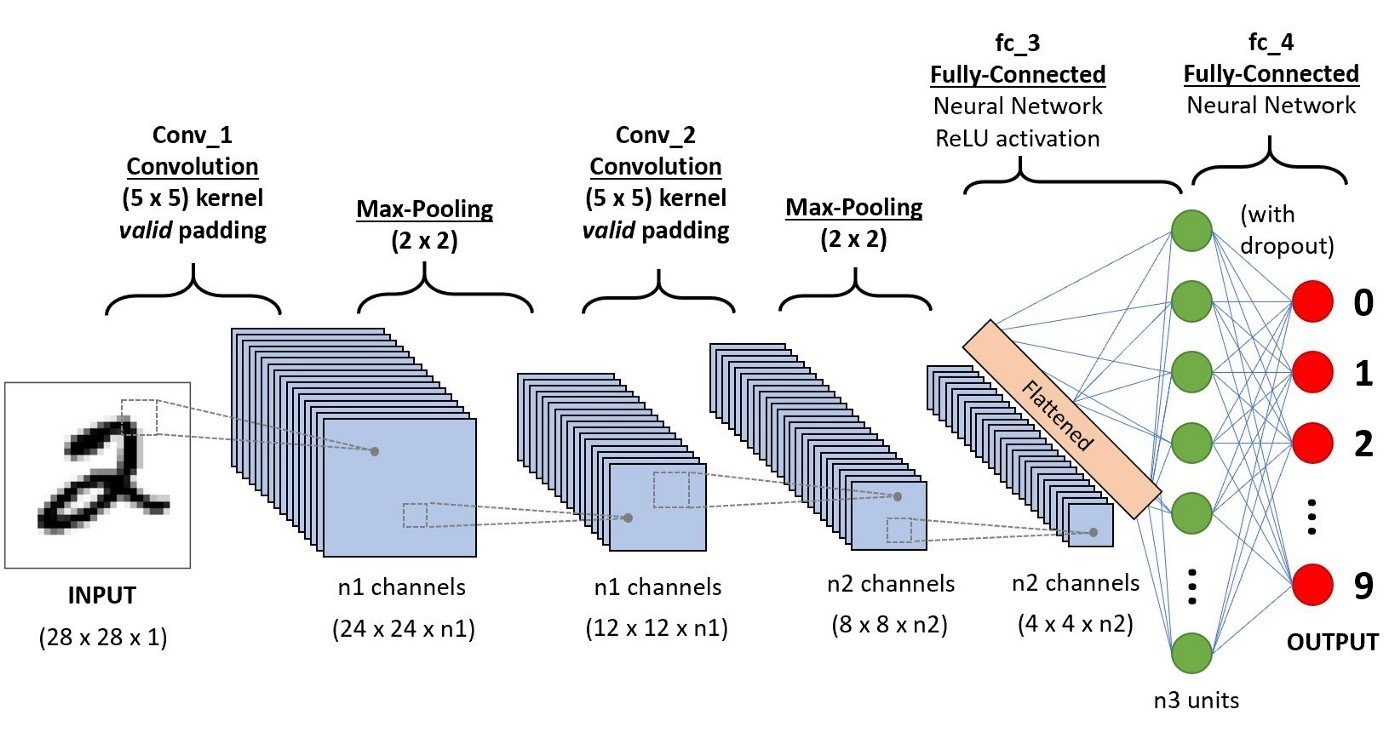
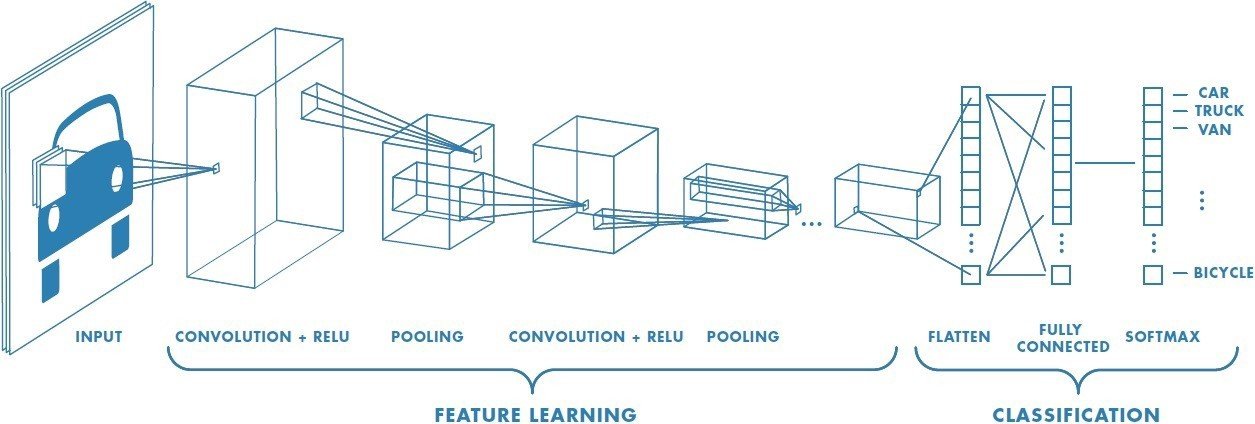
Ejemplo SOTA: You Only Look Once
Algunos últimos detalles relevantes para CNNs
Data Augmentation

Transfer learning
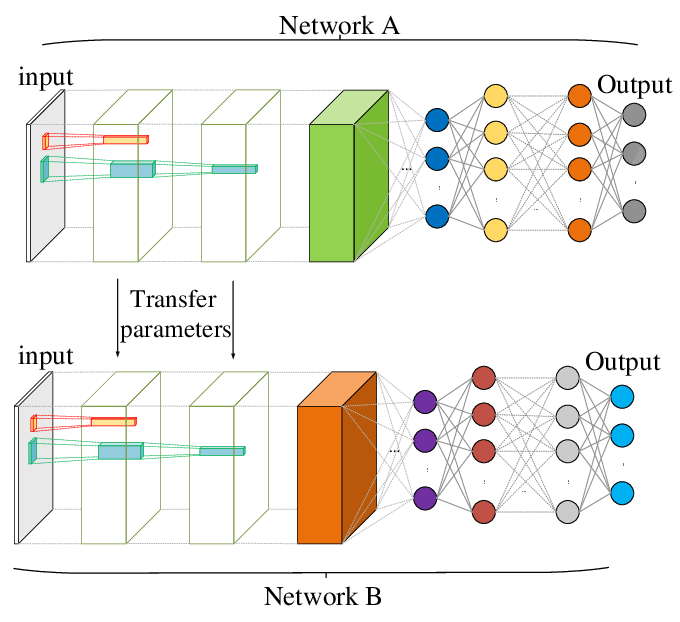
red A
(pre-entrenada)
Transfer learning

red A
(pre-entrenada)
Transfer learning

red A
(pre-entrenada)
red B
(a entrenar)
Transfer learning

red A
(pre-entrenada)
red B
(a entrenar)
Transfer learning

red A
(pre-entrenada)
red B
(a entrenar)
nuevas categorías
nuevos ejemplos
Transfer learning

red A
(pre-entrenada)
red B
(a entrenar)
nuevas categorías
nuevos ejemplos
queda constante, no hay que volver a entrenar
Transfer learning

red A
(pre-entrenada)
red B
(a entrenar)
nuevas categorías
nuevos ejemplos
sólo se entrena esto
Finetuning

red A
(pre-entrenada)
Finetuning

red A
(pre-entrenada)
nuevas categorías
Finetuning

red A
(pre-entrenada)
nuevas categorías
nuevos ejemplos
se re-entrena la red completa, empleando los pesos pre-entrenados como "valor inicial"
Otros ejemplos de redes especializadas (dentro de muchas, muchas, muchas más)
Residual Networks (ResNets)
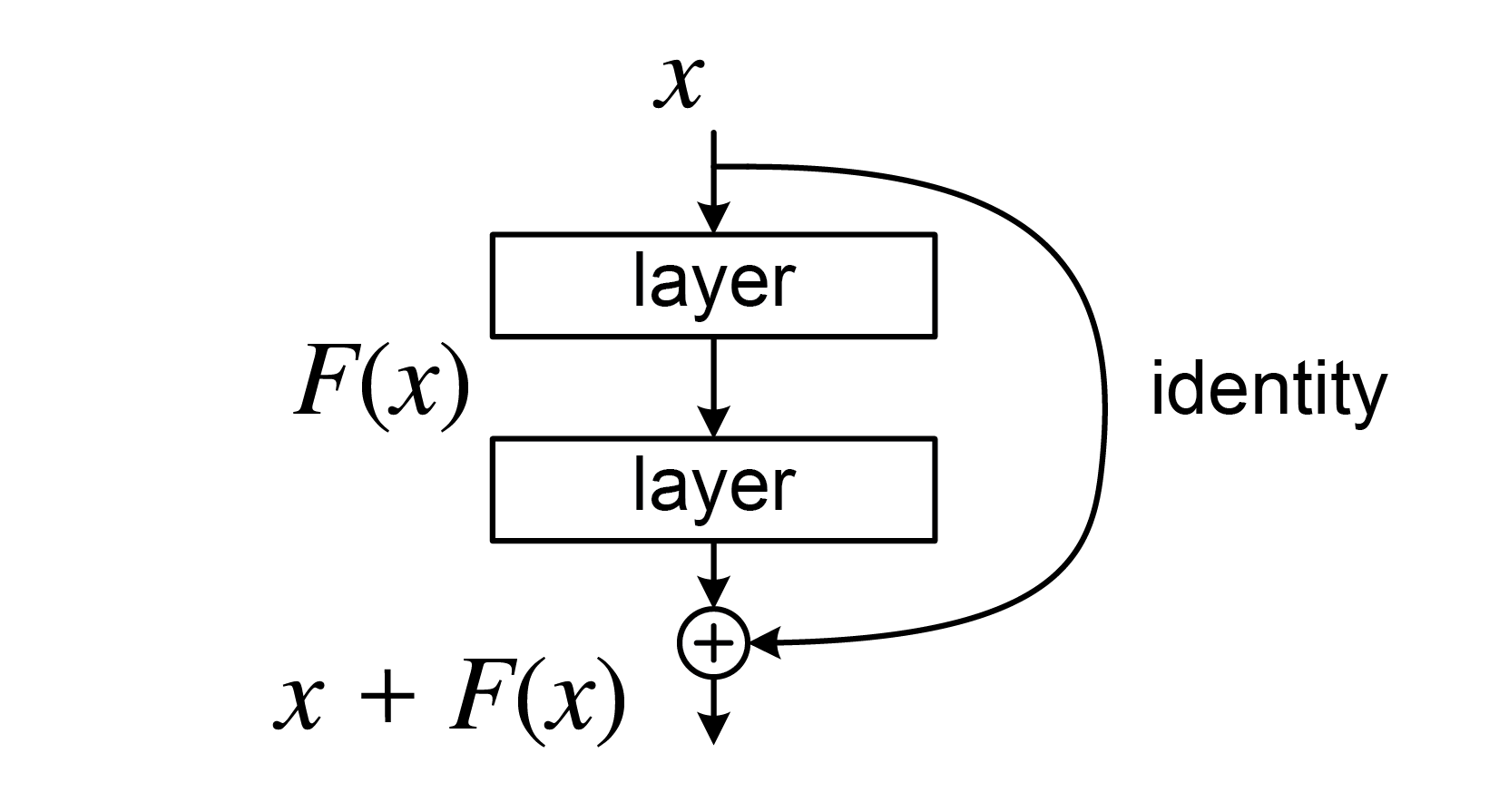
Transformer Networks (ej. ChatGPT)
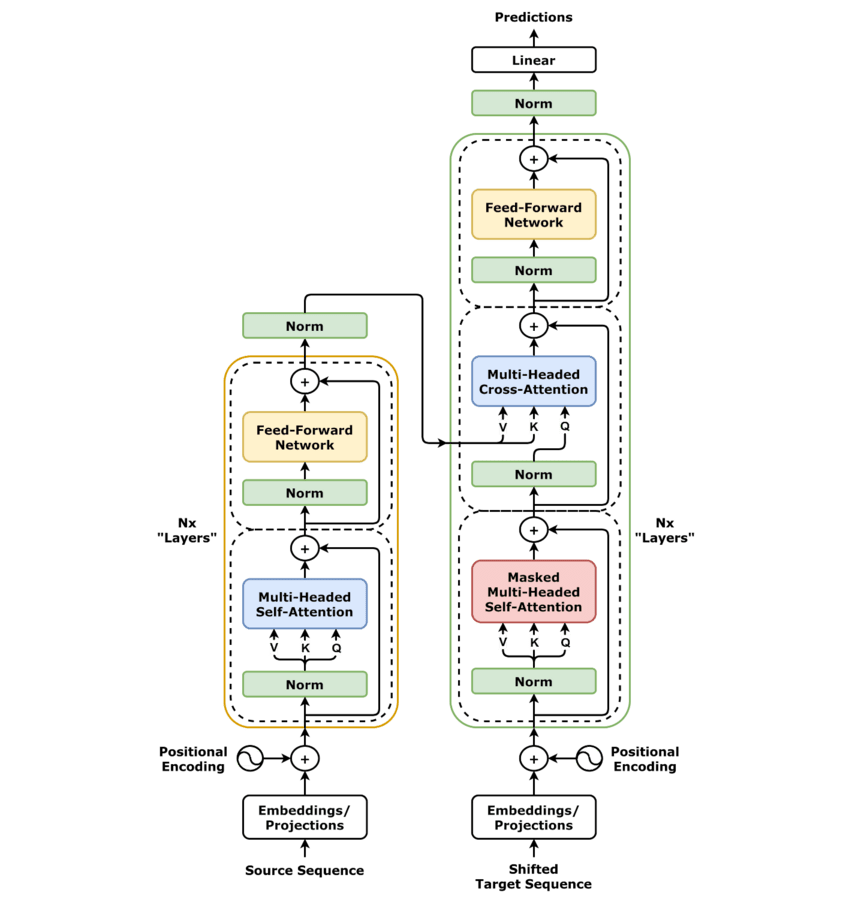
Referencias
- S. Prince, Understanding Deep Learning, capítulo 10.
- https://d2l.ai/chapter_convolutional-neural-networks/index.html
- https://d2l.ai/chapter_convolutional-modern/index.html