Attention Mechanisms
December 2, 2020



Marcos V. Treviso
Deep Structured Learning
Fall 2020
Acknowledgments
Neural Attention Mechanisms by Ben Peters
Learning with Sparse Latent Structure by Vlad Niculae
Seq2Seq and Attention by Lena Voita
The elephant in the interpretability room by Jasmijn Bastings
The illustrated transformer
http://jalammar.github.io/illustrated-transformer/
The annotated transformer
http://nlp.seas.harvard.edu/2018/04/03/attention.html
Łukasz Kaiser’s presentation
https://www.youtube.com/watch?v=rBCqOTEfxvg
⚙️
🎩
🖼
📖
Summary
Quick recap on RNN-based seq2seq models
Self-attention networks
Attention and its different flavors
Attention interpretability
🗞
🍭
🤳
🔍
dense • sparse • soft • hard • structured
The Transformer
Can we consider attention maps as explanation?
Why attention?
- Attention is a recent and important component to the success of modern neural networks
- We want neural nets that automatically weigh relevance of the input and use these weights to perform a task
- Main advantages:
- performance gain
- none or few parameters
- fast (easy to parallelize)
- drop-in implementation
- tool for "interpreting" predictions
🎯
☁️
⚡️
⚓️
🔍
Example

Example

Brief history
- "first" introduced in NLP for Machine Translation by Bahdanau et al. (2015)
"dynamic alignments"
"biological retina" glimples
"visual attention"
"inner attention"
"word attention"
"memory networks"
Brief history
- "first" introduced in NLP for Machine Translation by Bahdanau et al. (2015)
"dynamic alignments"
"biological retina" glimpes
"visual attention"
"inner attention"
"word attention"
"memory networks"
🌟
📸 Vision
⠇
🎙 Speech
⠇
📄 NLP
⠇
Attention in NLP

RNN-based seq2seq
context vector
Encoder
Decoder
↺
↺
BiLSTM
LSTM
$$x_1 \, x_2 \,...\, x_n$$
$$y_1 \, y_2 \,...\, y_m$$
RNN-based seq2seq
Encoder
Decoder
↺
↺
BiLSTM
LSTM
$$x_1 \, x_2 \,...\, x_n$$
$$y_1 \, y_2 \,...\, y_m$$
this bottleneck is problematic!
context vector
RNN-based seq2seq
Encoder
Decoder
BiLSTM
LSTM
$$x_1 \, x_2 \,...\, x_n$$
context vector
$$y_1 \, y_2 \,...\, y_m$$
↺
↺
RNN-based seq2seq
Encoder
Decoder
BiLSTM
LSTM
$$x_1 \, x_2 \,...\, x_n$$
context vector
$$y_1 \, y_2 \,...\, y_m$$
↺
↺
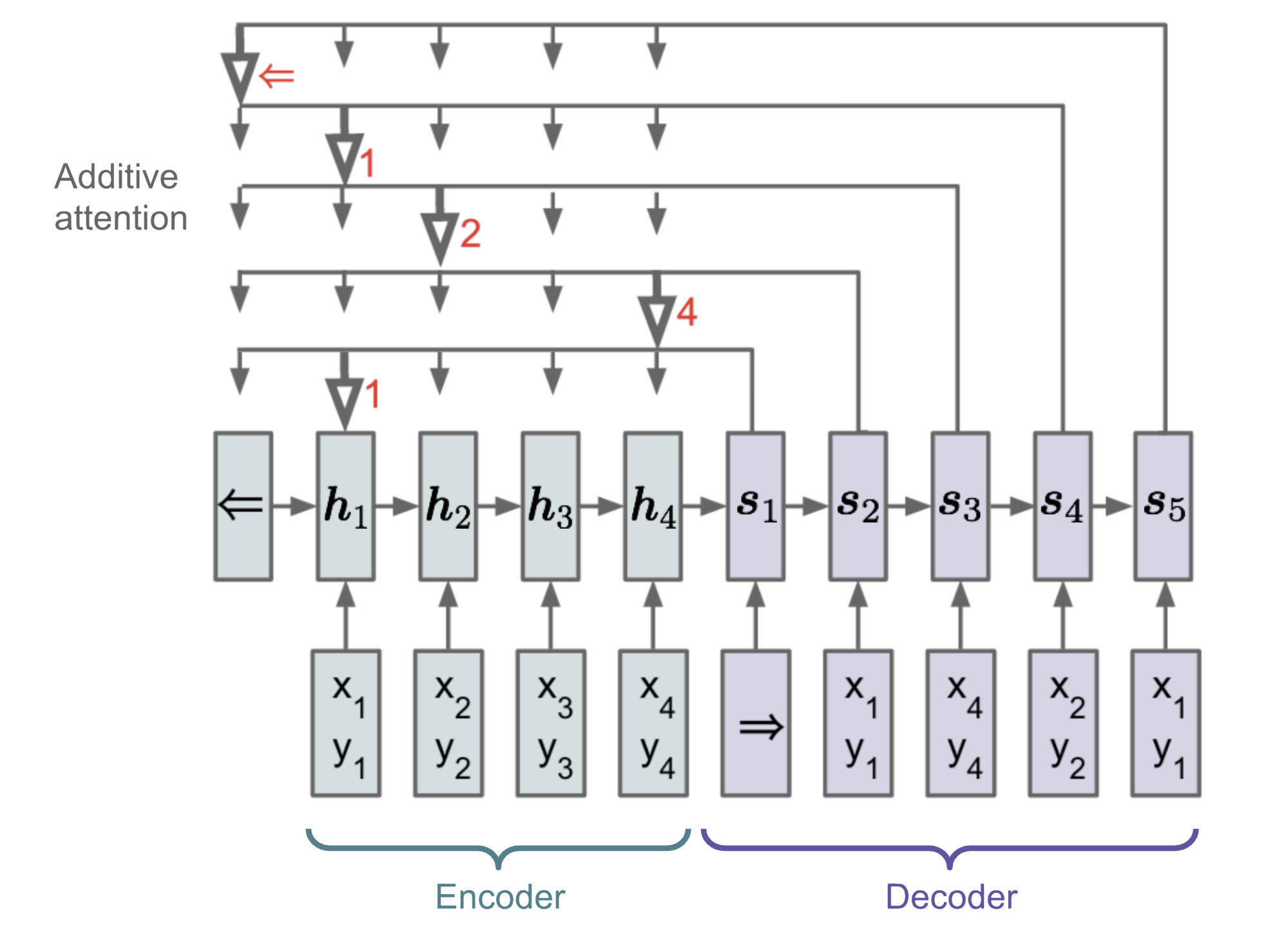
Attention Mechanism!
Attention mechanism
$$h_1$$
$$h_2$$
$$h_i$$
$$h_n$$
$$x_1$$
$$x_2$$
$$x_i$$
$$x_n$$
...
...
...
...
$$y_{j-1}$$
$$y_j$$
...
...
$$\mathrm{Attention}$$
$$q_{j-1}$$
$$q_j$$
$$c_j$$
- Bahdanau et al. (2015)
Attention mechanism
$$\mathrm{score\ function}$$
$$h_1 \, ...\,h_i \,...\, h_n$$
$$q_{j-1}$$
$$\theta_1 \, ...\,\theta_i \,...\, \theta_n$$
$$\mathrm{softmax}$$
$$p_1 \, ...\,p_i \,...\, p_n$$
$$c_j$$
$$\mathrm{weighted\ sum}$$
$$h_1$$
$$h_2$$
$$h_i$$
$$h_n$$
$$x_1$$
$$x_2$$
$$x_i$$
$$x_n$$
...
...
...
...
$$y_{j-1}$$
$$y_j$$
...
...
$$\mathrm{Attention}$$
$$q_{j-1}$$
$$q_j$$
$$c_j$$
- Bahdanau et al. (2015)
Attention mechanism
- Bahdanau et al. (2015)
$$\mathrm{score\ function}$$
$$h_1 \, ...\,h_i \,...\, h_n$$
$$q_{j-1}$$
$$\mathrm{softmax}$$
$$p_1 \, ...\,p_i \,...\, p_n$$
$$c_j$$
$$\mathrm{weighted\ sum}$$
query
keys
values
$$\theta_1 \, ...\,\theta_i \,...\, \theta_n$$
$$h_1$$
$$h_2$$
$$h_i$$
$$h_n$$
$$x_1$$
$$x_2$$
$$x_i$$
$$x_n$$
...
...
...
...
$$y_{j-1}$$
$$y_j$$
...
...
$$\mathrm{Attention}$$
$$q_{j-1}$$
$$q_j$$
$$c_j$$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
dot-product:
bilinear:
additive:
neural net:
$$\mathbf{k}_j^\top \mathbf{q}, \quad (d_q == d_k)$$
$$\mathbf{k}_j^\top \mathbf{W} \mathbf{q}, \quad \mathbf{W} \in \mathbb{R}^{d_k \times d_q}$$
$$\mathbf{v}^\top \mathrm{tanh}(\mathbf{W}_1 \mathbf{k}_j + \mathbf{W}_2 \mathbf{q})$$
$$\mathrm{MLP}(\mathbf{q}, \mathbf{k}_j); \quad \mathrm{CNN}(\mathbf{q}, \mathbf{K}); \quad ...$$
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
2. Map scores to probabilities
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
$$\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
2. Map scores to probabilities
softmax:
sparsemax:
$$ \exp(\boldsymbol{\theta}_j) / \sum_k \exp(\boldsymbol{\theta}_k) $$
$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \boldsymbol{\theta}||_2^2 $$
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
$$\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
2. Map scores to probabilities
3. Combine values
$$\mathbf{z} = \mathbf{V}^\top \mathbf{p} =\sum\limits_{i=1}^{m} \mathbf{V}_i \mathbf{p}_i \in \mathbb{R}^{d_v}$$
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
$$\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
2. Map scores to probabilities
3. Combine values
$$\mathbf{z} = \mathbf{V}^\top \mathbf{p} =\sum\limits_{i=1}^{m} \mathbf{V}_i \mathbf{p}_i \in \mathbb{R}^{d_v}$$
not necessarily in the simplex! e.g.
$$\mathbf{p} = \mathrm{sigmoid}(\boldsymbol{\theta}) $$
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
$$\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} $$
Attention mechanism
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\boldsymbol{\theta} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} $$
3. Combine values
$$\mathbf{z} = \mathbf{V}^\top \mathbf{p} =\sum\limits_{i=1}^{m} \mathbf{V}_i \mathbf{p}_i \in \mathbb{R}^{d_v}$$
but in this lecture:
$$\sum_i \mathbf{p}_i = 1 \, \\ \forall i, \mathbf{p}_i \geq 0$$
Attention mechanism
def attention(query, keys, values=None):
"""
query.shape is (batch_size, 1, d)
keys.shape is (batch_size, n, d)
values.shape is (batch_size, n, d)
"""
# use keys as values
if values is None:
values = keys
# STEP 1. scores.shape is (batch_size, 1, n)
scores = torch.matmul(query, keys.transpose(-1, -2))
# STEP 2. probas.shape is (batch_size, 1, n)
probas = torch.softmax(scores, dim=-1)
# STEP 3. c_vector.shape is (batch_size, 1, d)
c_vector = torch.matmul(probas, values)
return c_vector
Attention flavors
- Interaction between \( \mathbf{q}, \mathbf{K}, \mathbf{V} \):
- Self-attention: \(\mathbf{q} = \mathbf{k}_j\)

Attention flavors
- Interaction between \( \mathbf{q}, \mathbf{K}, \mathbf{V} \):
- Hierarchical:
- word-level \(\mathbf{q}_w, \mathbf{K}_w\)
- sentence-level \(\mathbf{q}_s, \mathbf{K}_s\)
- Hierarchical:

Dense vs Sparse
Dense: \( |\mathrm{supp}(\mathbf{p})| = n\)
- \(\mathbf{p} = \pi(\boldsymbol{\theta}) \in \triangle^{n} \)


Sparse: \( |\mathrm{supp}(\mathbf{p})| < n\)
Variational form of argmax
Fundamental Thm. Lin. Prog.
(Dantzig et al., 1955)
Variational form of argmax
1
1
$$n=2$$
$$\boldsymbol{\theta} = [0.4, 1.4]$$
Fundamental Thm. Lin. Prog.
(Dantzig et al., 1955)
Variational form of argmax
1
1
$$n=2$$
$$\boldsymbol{\theta} = [0.4, 1.4]$$
$$\mathbf{p}^\star = [0,1]$$
Fundamental Thm. Lin. Prog.
(Dantzig et al., 1955)
Variational form of argmax
1
1
$$n=2$$
1
1
1
$$n=3$$
$$\boldsymbol{\theta} = [0.4, 1.4]$$
$$\mathbf{p}^\star = [0,1]$$
$$\boldsymbol{\theta} = [0.3, 0.1, 1.5]$$
Fundamental Thm. Lin. Prog.
(Dantzig et al., 1955)
Variational form of argmax
1
1
$$n=2$$
1
1
1
$$n=3$$
$$\boldsymbol{\theta} = [0.4, 1.4]$$
$$\mathbf{p}^\star = [0,1]$$
$$\mathbf{p}^\star = [0,0,1]$$
$$\boldsymbol{\theta} = [0.3, 0.1, 1.5]$$
Fundamental Thm. Lin. Prog.
(Dantzig et al., 1955)
Smoothed max operators
$$\triangle^3$$
argmax:
Smoothed max operators
$$\triangle^3$$
argmax:
softmax:
Smoothed max operators
$$\triangle^3$$
argmax:
softmax:
sparsemax:
Smoothed max operators
$$\triangle^3$$
argmax:
softmax:
sparsemax:
\(\alpha\)-entmax:
Sparsemax and α-entmax
sparsemax
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Sparsemax and α-entmax
sparsemax
α-entmax
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Sparsemax and α-entmax
sparsemax
α-entmax
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Jacobian:
Sparsemax and α-entmax
sparsemax
α-entmax
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
Just compute \(\boldsymbol{\tau}\):
\(O(n\log n)\) or \(O(n)\)*
(Martins and Astudillo, 2016)
* (Peters, Niculae, and Martins, 2019)
Jacobian:
\(p^\star = [.99, .01, 0] \implies \mathbf{s}=[1,1,0]\)
\(p^\star = [.50, .50, 0] \implies \mathbf{s}=[1,1,0]\)
The Jacobian of sparsemax (\(\alpha=2\)) depends only on the support and not on the actual values of \(\mathbf{p}^\star\)
Sparsemax and α-entmax

Tsallis α-entropy regularizer
\(\theta\)
Sparsemax and α-entmax

softmax
sparsemax
Soft attention
differentiable node
e.g. softmax/sparsemax
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
\(\boldsymbol{\theta}\)
Hard attention
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
argmax node
\(\boldsymbol{\theta}\)
Hard attention
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
argmax node
\(\boldsymbol{\theta}\)
Hard attention
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
argmax node
\(\boldsymbol{\theta}\)
Hard attention
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
argmax node
\(\boldsymbol{\theta}\)
Hard attention
Encoder
Decoder
BiLSTM
LSTM
↺
↺
\(\mathbf{p}\)
\(\theta_3\)
\(p_3\)
argmax node
\(\boldsymbol{\theta}\)
Soft vs Hard
Soft
"smooth selection"
Continuous representation
"soft" decisions
Differentiable
Just backprop!
Hard
"subset selection"
Discrete representation
"binary" decisions
Non differentiable
REINFORCE / surrogate gradients / reparameterization trick / perturb-and-MAP / etc.
Structured attention
- Structural biases?
- When you generate “Vou”, where do you attend?
- Can we consider the sequential structure of our input/output?
- Note: \(\boldsymbol{\pi}(\boldsymbol{\theta}) \in \triangle^n\)
I am going to the store → Vou à loja
I am going to the store → Vou à loja
I am going to the store → Vou à loja
I am going to the store → Vou à loja
Fusedmax
$$\triangle^3$$
argmax:
softmax:
sparsemax:
\(\alpha\)-entmax:
fusedmax:
Fusedmax
$$\triangle^3$$
argmax:
softmax:
sparsemax:
\(\alpha\)-entmax:
fusedmax:
penalize weight differences between adjacent positions
Fusedmax

Latent structured attention

- Consider binary variables (sigmoids) \(z_i\) instead of \(\boldsymbol{\pi}(\boldsymbol{\theta})\)
- Structured: linear dependencies on \(z_i\)
- Linear-chain CRF
- Use marginals from forward-backward
\(\pi(\theta)\)
independent \(z_i\)
linear dependencies on \(z_i\)
Latent structured attention

- Consider binary variables (sigmoids) instead of \(\boldsymbol{\pi}(\boldsymbol{\theta})\)
- Structured: linear dependencies on \(z_i\)
- Linear-chain CRF
- Use marginals from forward-backward
\(\pi(\theta)\)
independent \(z_i\)
linear dependencies on \(z_i\)
Cons:
no sparsity
specialized backprop implementation
Latent structured attention

- Consider binary variables (sigmoids) instead of \(\boldsymbol{\pi}(\boldsymbol{\theta})\)
- Structured: linear dependencies on \(z_i\)
- Linear-chain CRF
- Use marginals from forward-backward
\(\pi(\theta)\)
independent \(z_i\)
linear dependencies on \(z_i\)
Cons:
no sparsity
specialized backprop implementation
An alternative: SparseMAP
structured counterpart of sparsemax
model any kind of structure (just need MAP)
plug & play implemenation
Drawbacks of RNNs
- Sequential mechanism prohibits parallelization
- Long-range dependencies are tricky, despite gating
$$x_1$$
$$x_2$$
...
$$x_n$$
$$x_1 \quad x_2 \quad x_3 \quad x_4 \quad x_5 \quad x_6 \quad x_7 \quad x_8 \quad x_9 \quad ... \quad x_{n-1} \quad x_{n}$$
Beyond RNN-based seq2seq
- Neural Turing Machines
- Memory networks
- Pointer networks
- Transformer

(finite-tape) Turing Machine
Pointer network
Pause
☕️ 🥪 🍃
Self-attention networks
Transformer

Transformer

Transformer
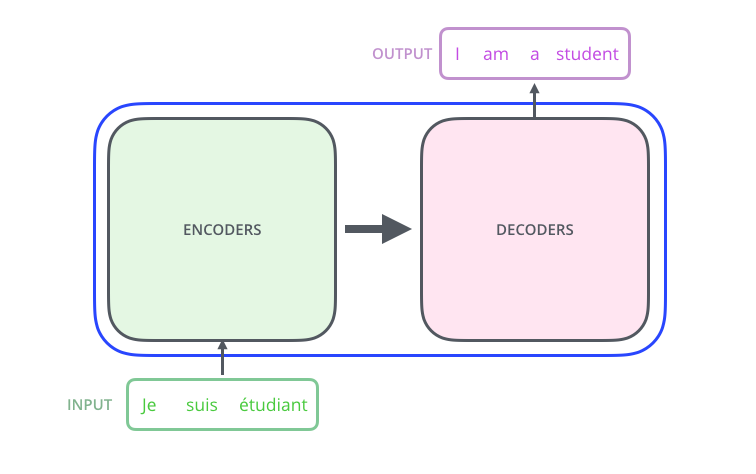
$$x_1 \, x_2 \,...\, x_n$$
$$\mathbf{r}_1 \, \mathbf{r}_2 \,...\, \mathbf{r}_n$$
$$y_1 \, y_2 \,...\, y_m$$
encode
decode
Transformer

Transformer
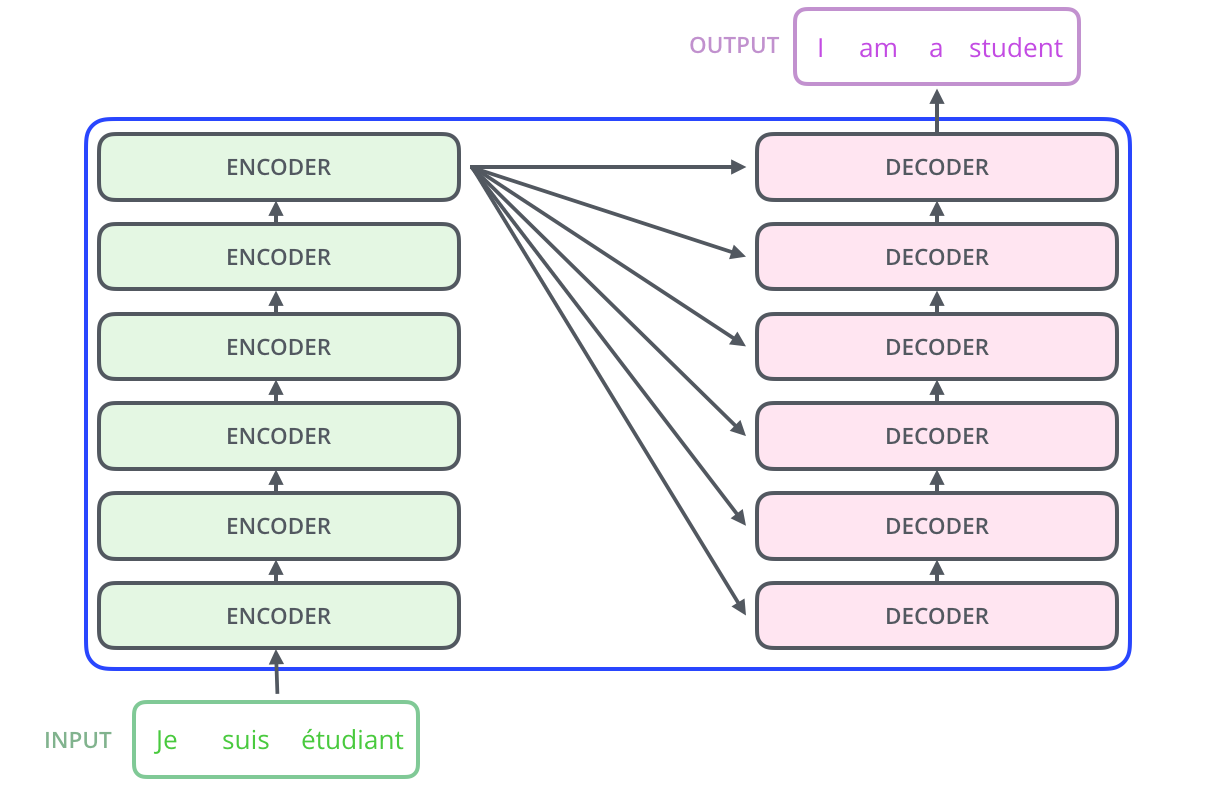
Transformer blocks
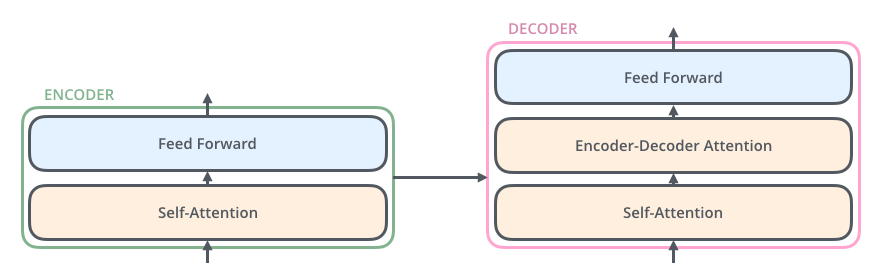
The encoder
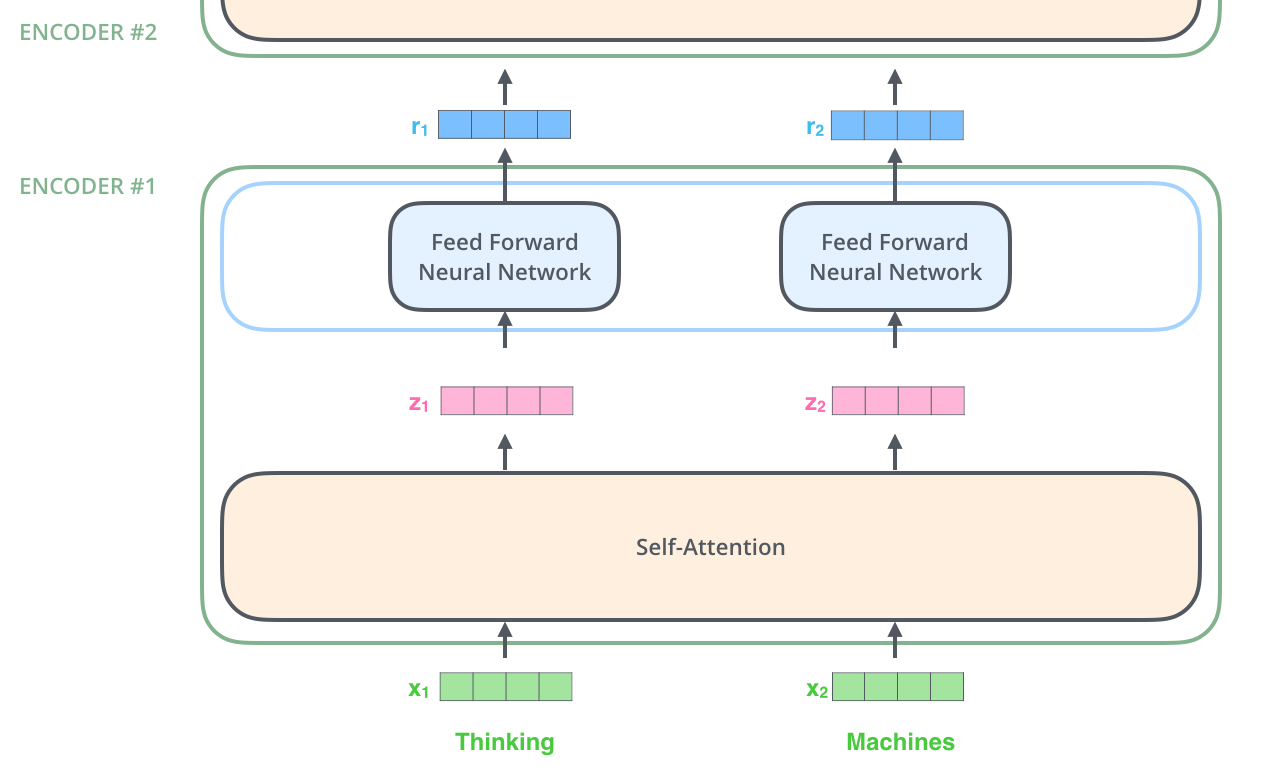
Self-attention

"The animal didn't cross the street because it was too tired"
Self-attention

"The animal didn't cross the street because it was too tired"
$$\mathbf{Q}_j = \mathbf{K}_j = \mathbf{V}_j \in \mathbb{R}^{d} \quad \iff$$
dot-product scorer!
Transformer self-attention
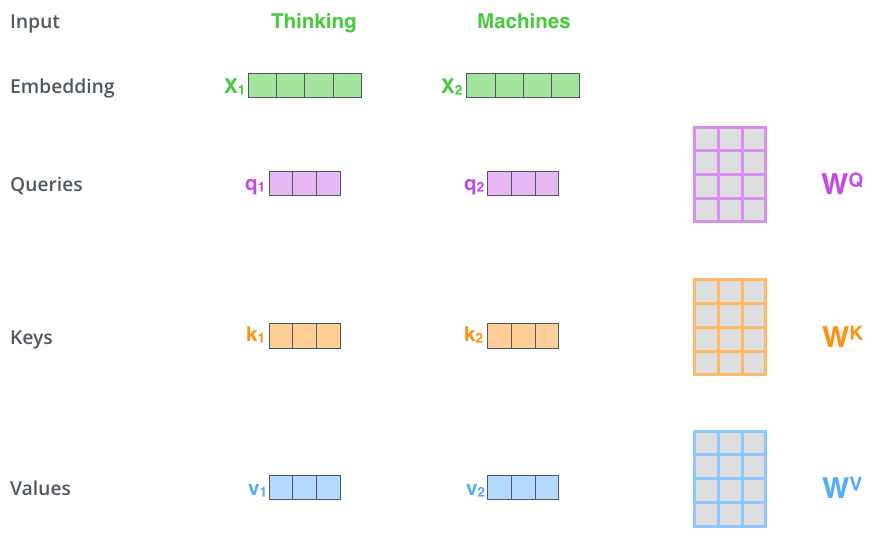
Transformer self-attention
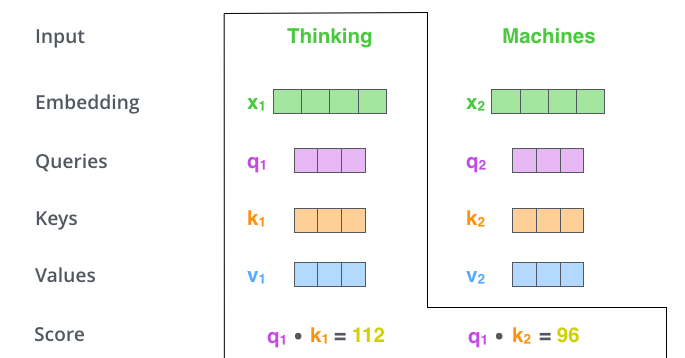
Transformer self-attention
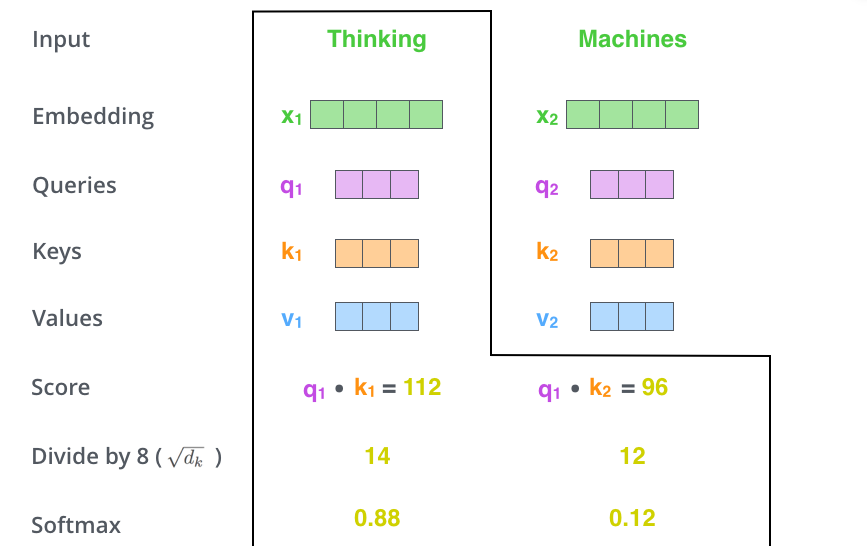
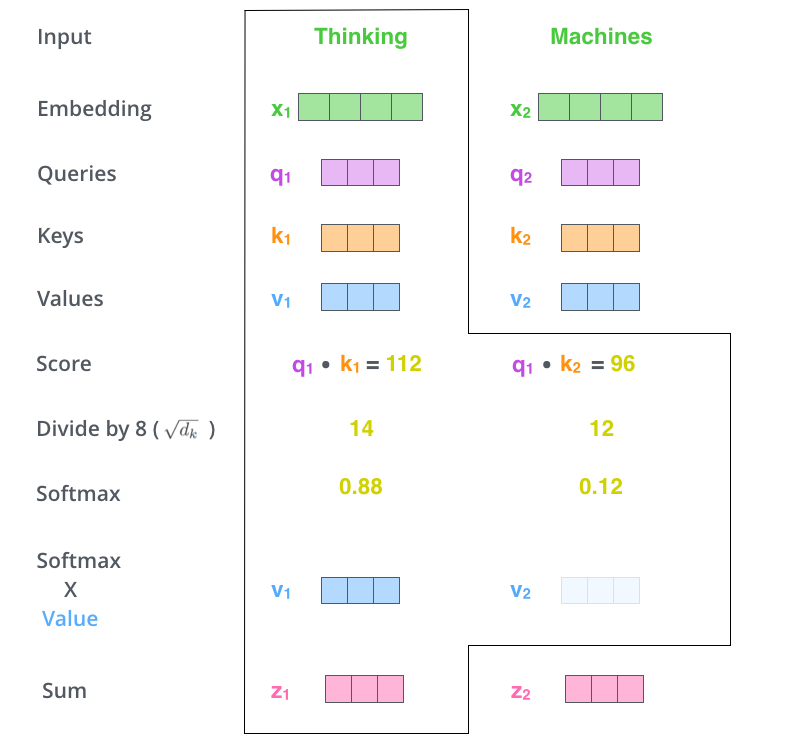
Matrix calculation
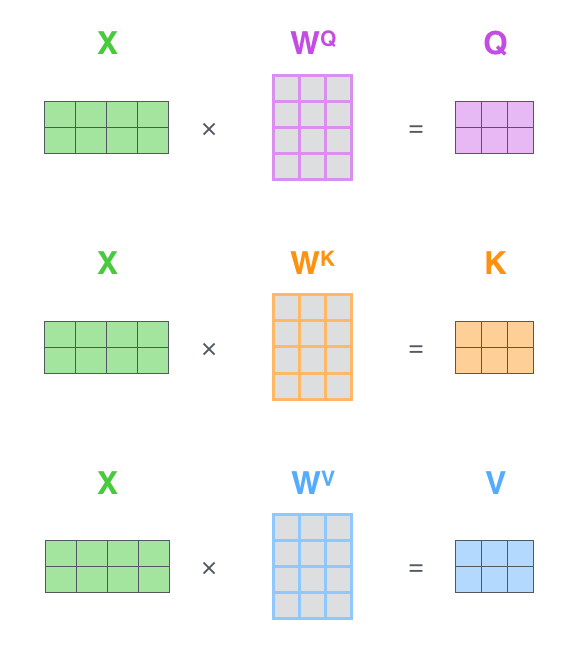
Matrix calculation
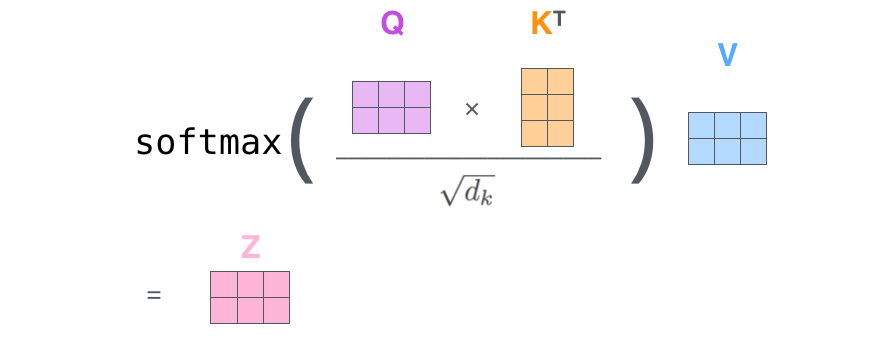
Matrix calculation
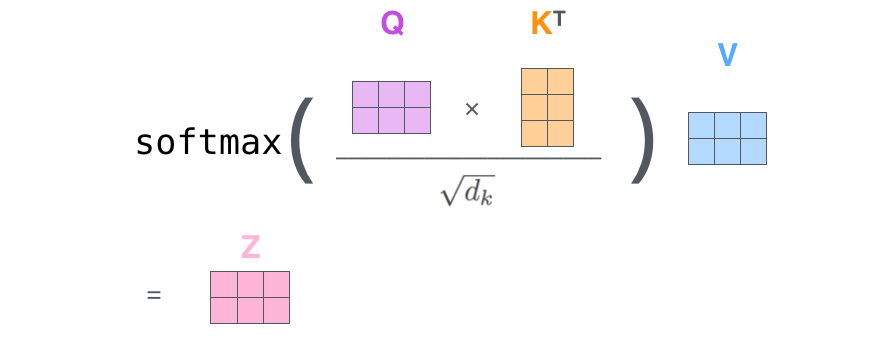
$$\mathbf{S} = \mathrm{score}(\mathbf{Q}, \mathbf{K}) \in \mathbb{R}^{n \times n} $$
$$\mathbf{P} = \pi(\mathbf{S}) \in \triangle^{n \times n} $$
$$\mathbf{Z} = \mathbf{P} \mathbf{V} \in \mathbb{R}^{n \times d}$$
$$\mathbf{Z} = \mathrm{softmax}\Big(\frac{\mathbf{Q} \mathbf{K}^\top}{\sqrt{d_k}}\Big) \mathbf{V} $$
$$\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{n \times d}$$
Problem of self-attention

- Convolution: a different linear transformation for each relative position
> Allows you to distinguish what information came from where
- Self-attention: a weighted average :(
Fix: multi-head attention
- Multiple attention layers (heads) in parallel
- Each head uses different linear transformations
- Attention layer with multiple “representation subspaces”

Multi-head attention

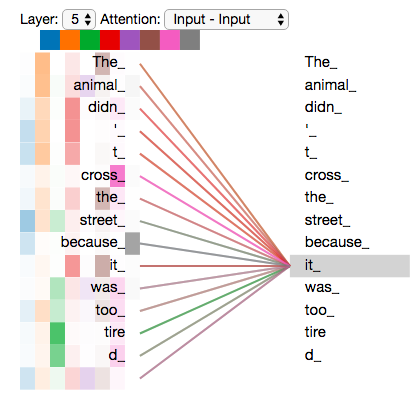
2 heads
all heads (8)
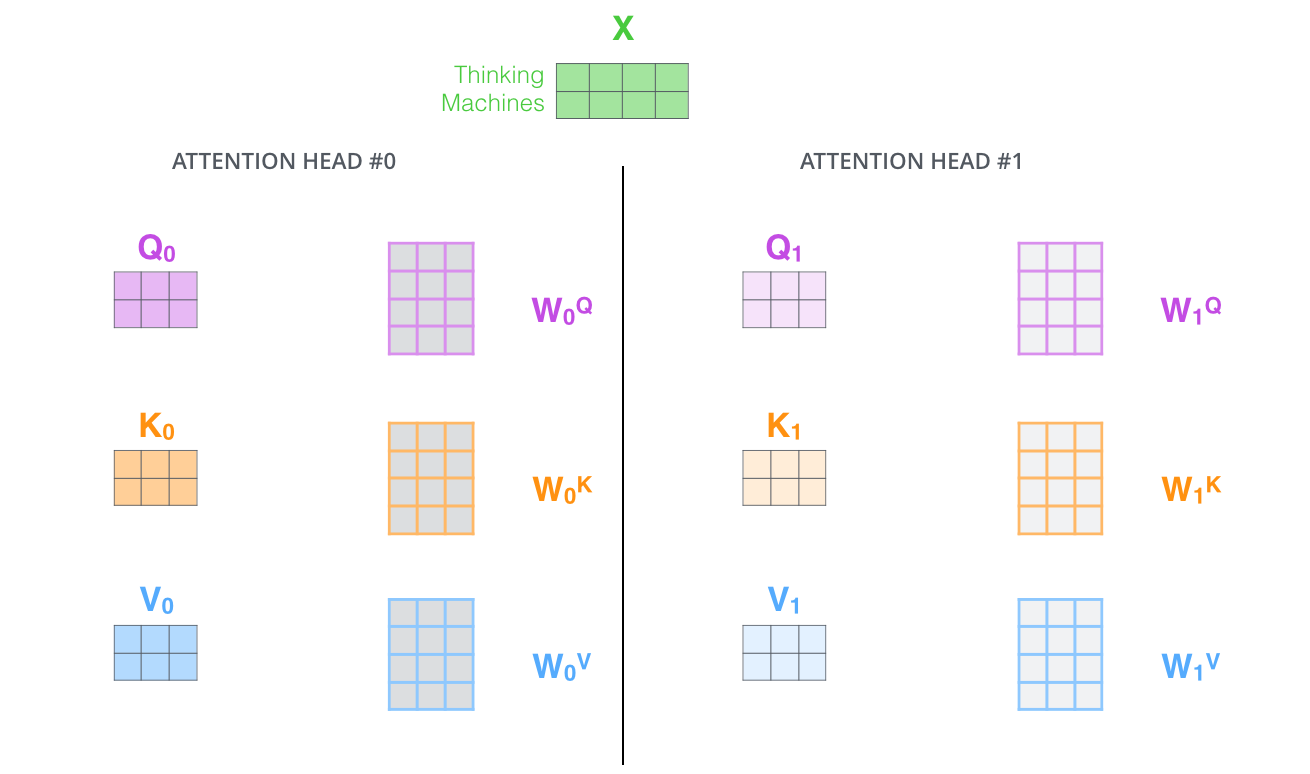
Multi-head attention
Multi-head attention
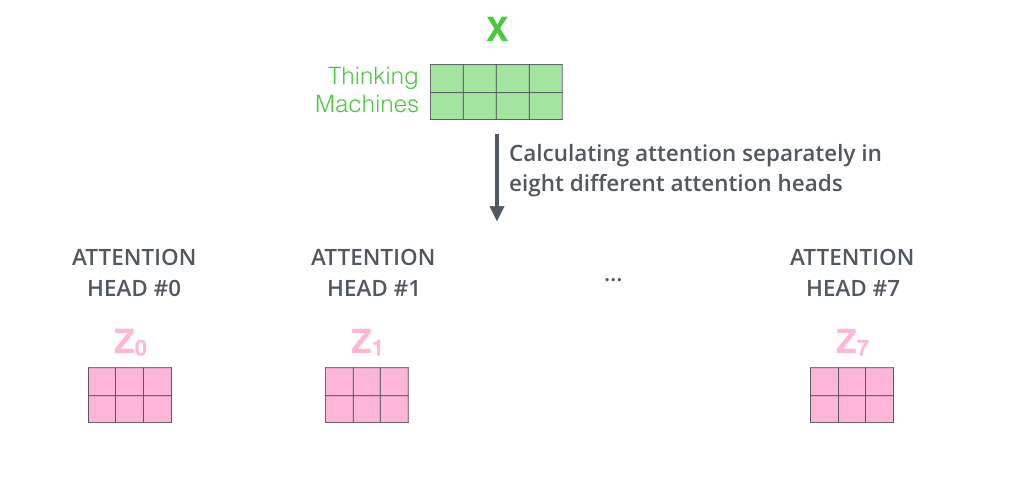
Multi-head attention
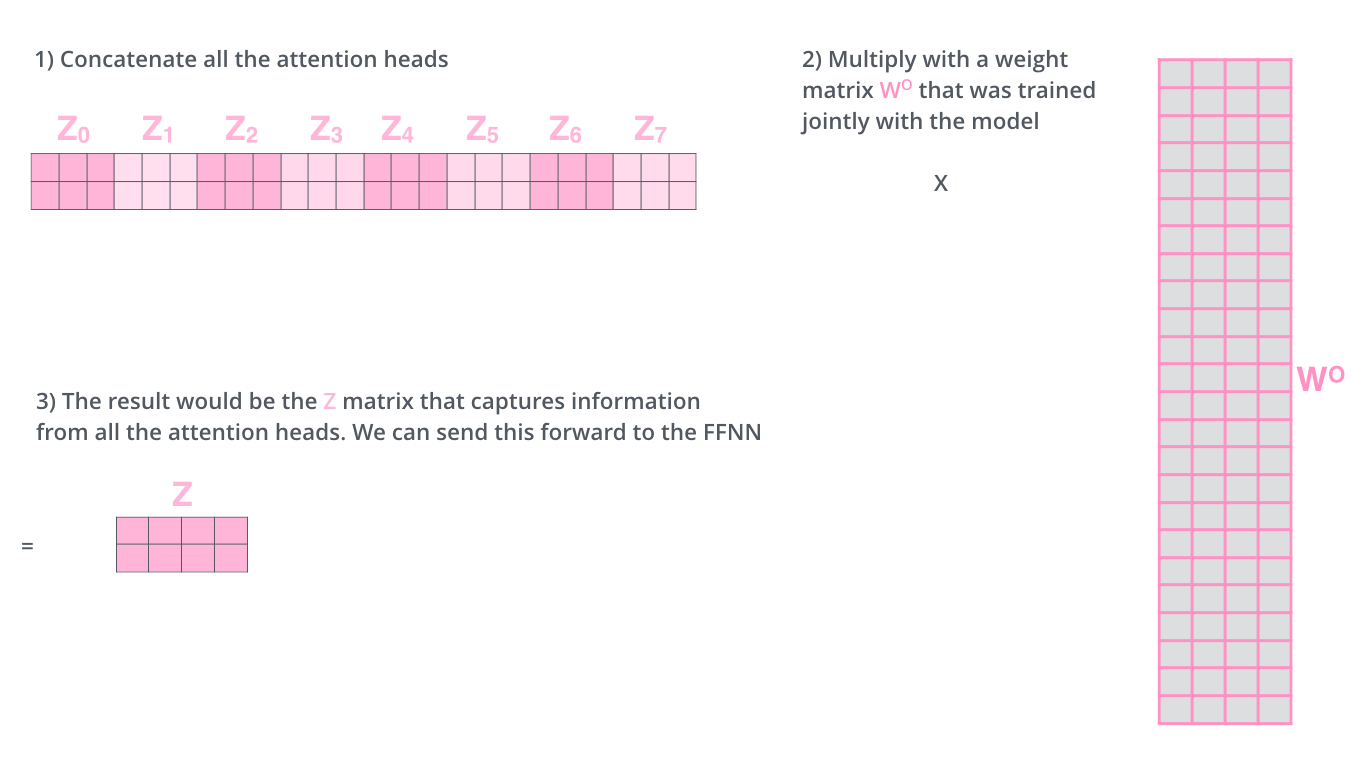
Multi-head attention

Multi-head attention
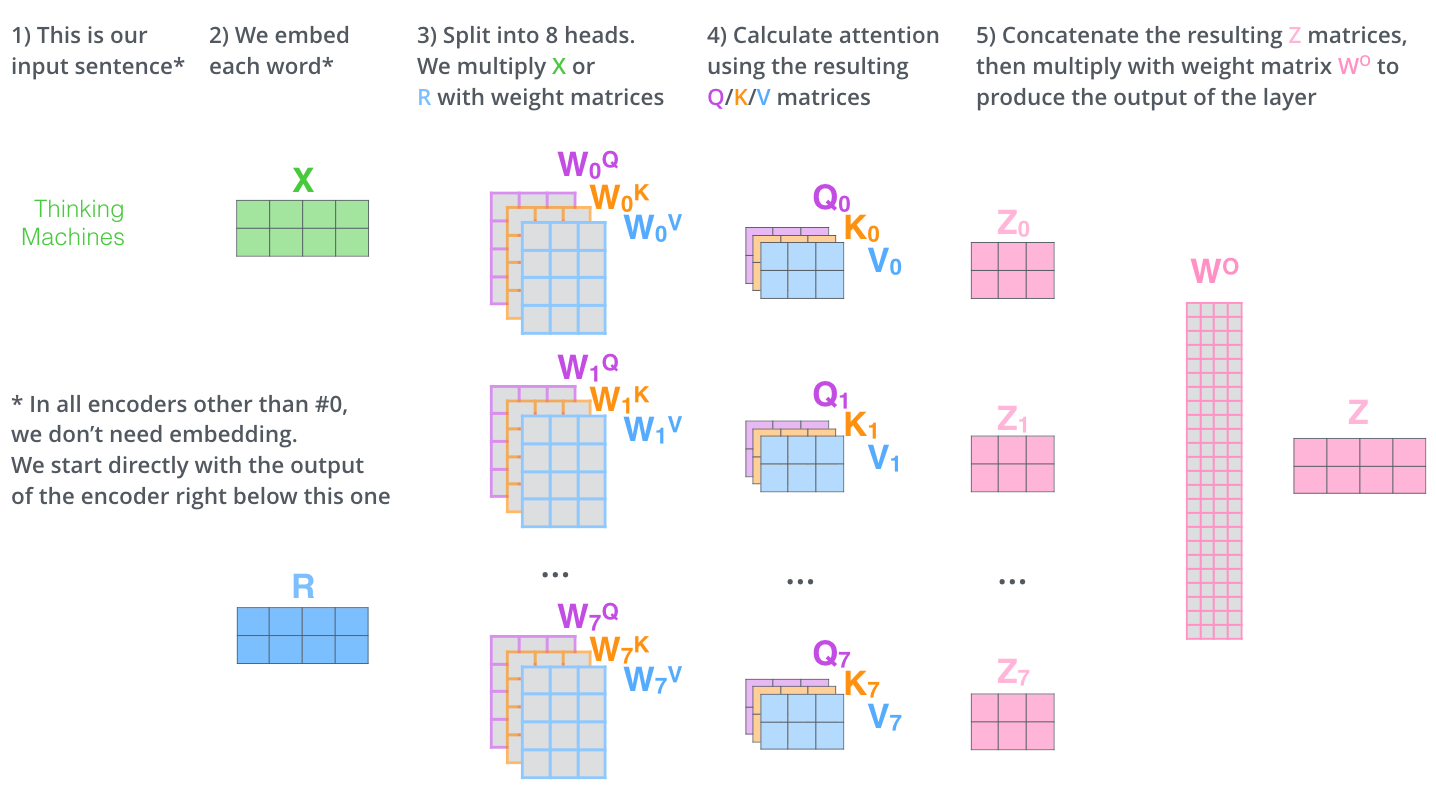
Implementation
class MultiHeadAttention(nn.Module)
def __init__(self, d_size, num_heads, dropout=0.0):
assert d_size % num_heads == 0
self.num_heads = num_heads
self.h_size = d_size // num_heads
self.linear_q = nn.Linear(d_size, self.h_size)
self.linear_k = nn.Linear(d_size, self.h_size)
self.linear_v = nn.Linear(d_size, self.h_size)
self.linear_o = nn.Linear(d_size, d_size)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values=None):
"""
queries.shape is (batch_size, m, d)
keys.shape is (batch_size, n, d)
values.shape is (batch_size, n, d)
"""
# use keys as values
if values is None:
values = keys
# do all linear projections
queries = self.linear_q(queries)
keys = self.linear_k(keys)
values = self.linear_v(values)
# split heads
batch_size = queries.shape[0]
queries = queries.view(batch_size, -1, self.num_heads, self.h_size).transpose(1, 2)
keys = keys.view(batch_size, -1, self.num_heads, self.h_size).transpose(1, 2)
values = values.view(batch_size, -1, self.num_heads, self.h_size).transpose(1, 2)
# new shapes:
# queries (batch_size, num_heads, m, h_size)
# keys (batch_size, num_heads, n, h_size)
# values (batch_size, num_heads, n, h_size)
# scores.shape is (batch_size, num_heads, m, n)
scores = torch.matmul(queries, keys.transpose(-1, -2)) / sqrt(self.h_size)
# probas.shape is (batch_size, num_heads, m, n)
probas = torch.softmax(scores, dim=-1)
probas = self.dropout(probas)
# cvector.shape is (batch_size, num_heads, m, h_size)
c_vector = torch.matmul(probas, values)
# reshape c_vector to (batch_size, m, d)
c_vector = c_vector.transpose(1, 2).reshape(batch_size, -1, self.num_heads * self.h_size)
# apply final linear projection
c_vector = self.linear_o(c_vector)
return c_vector
Positional encoding
- A way to account for the order of the words in the seq.
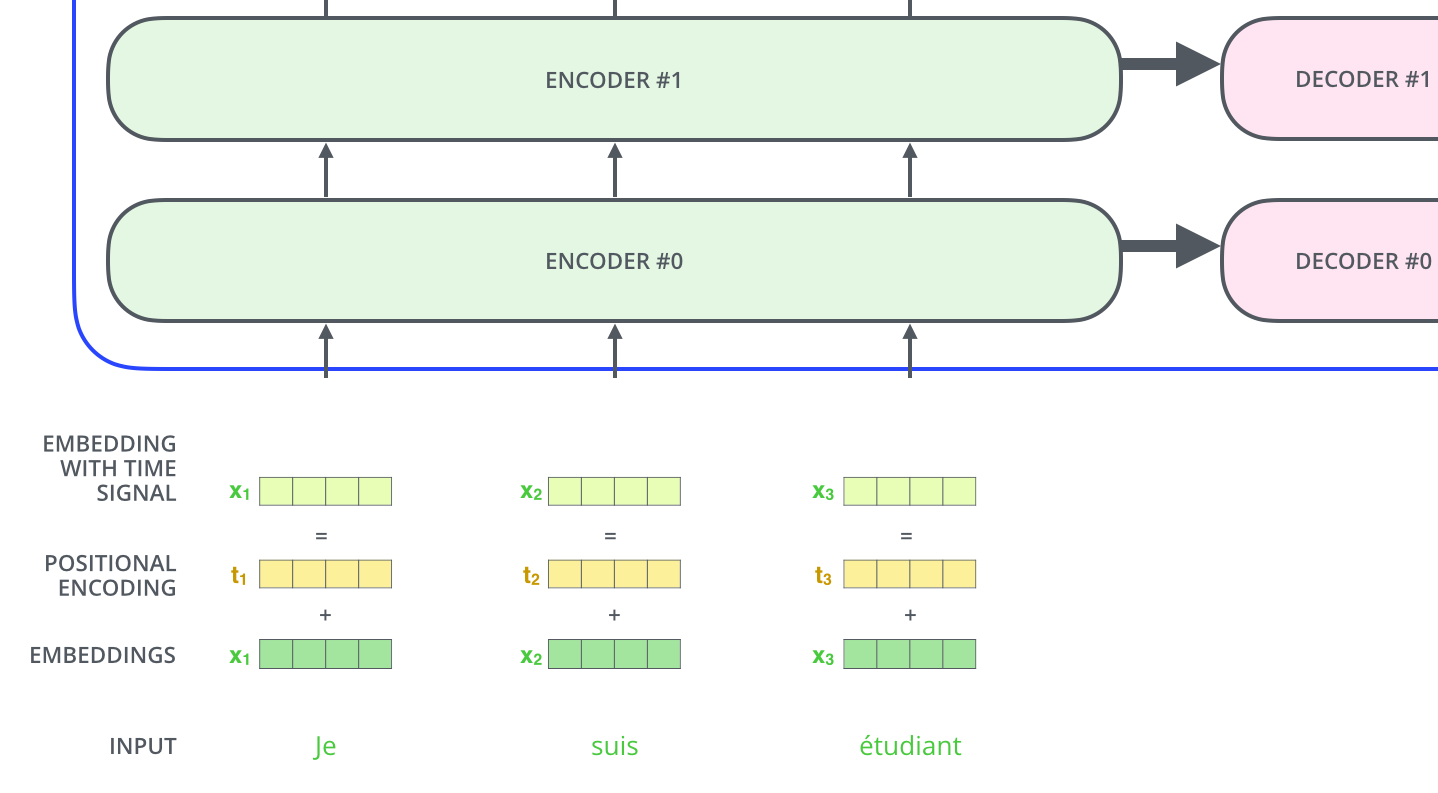
Positional encoding
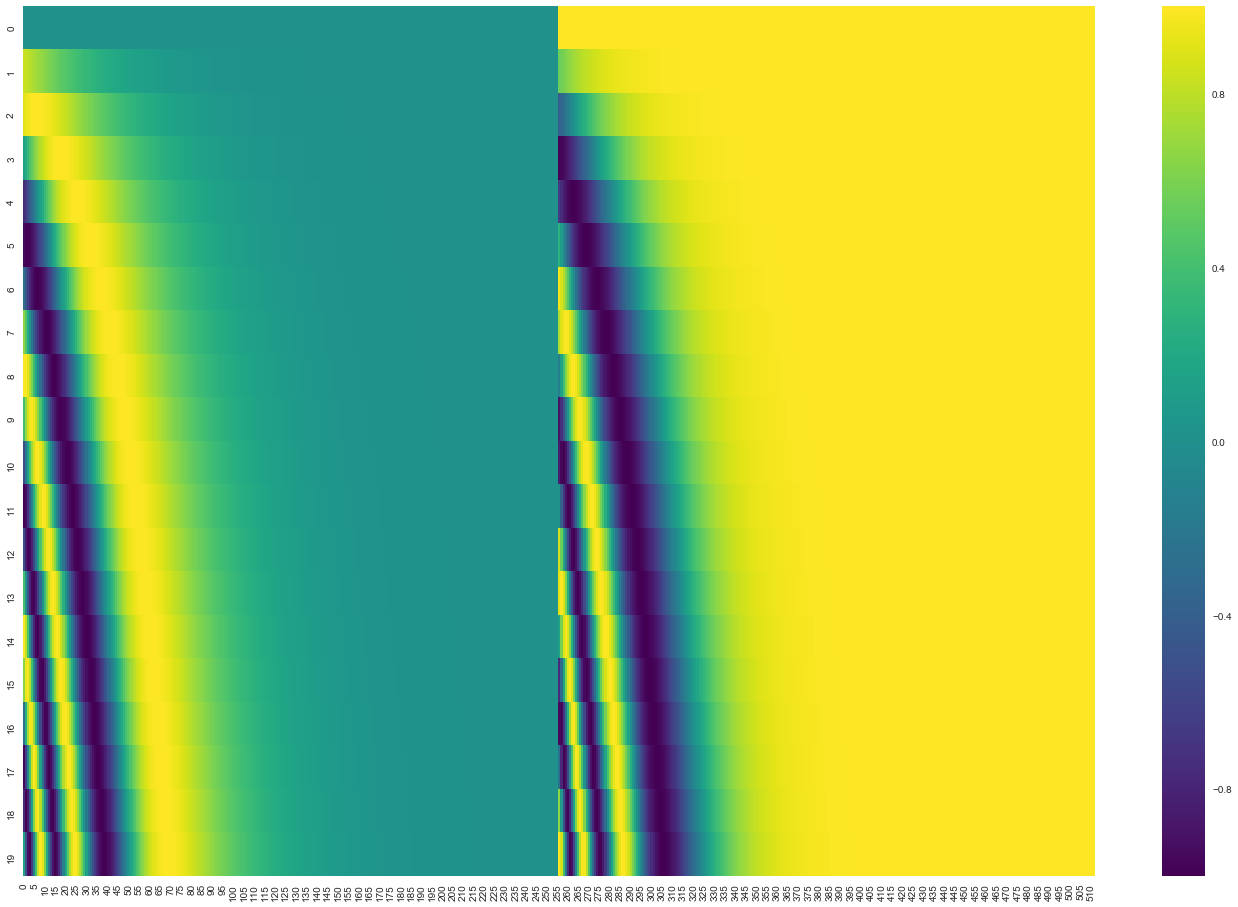
Positional encoding
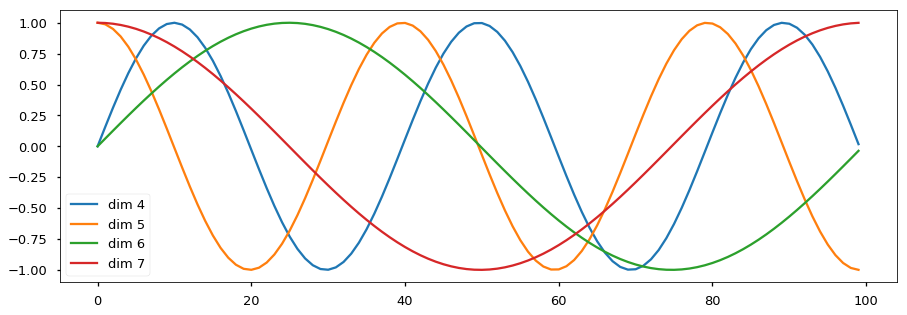
Residuals & LayerNorm
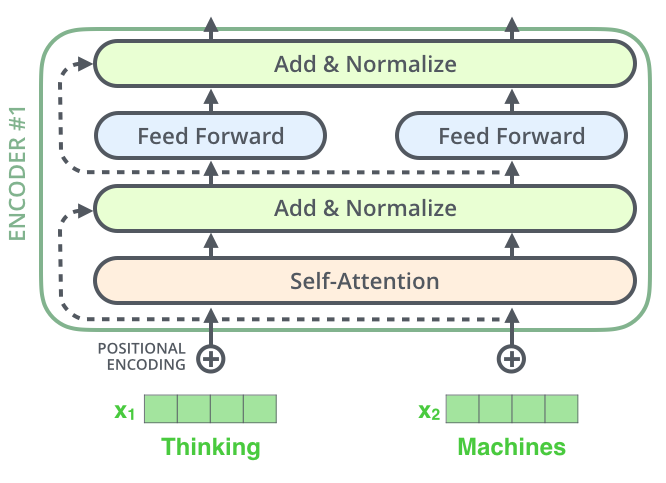
Residuals & LayerNorm
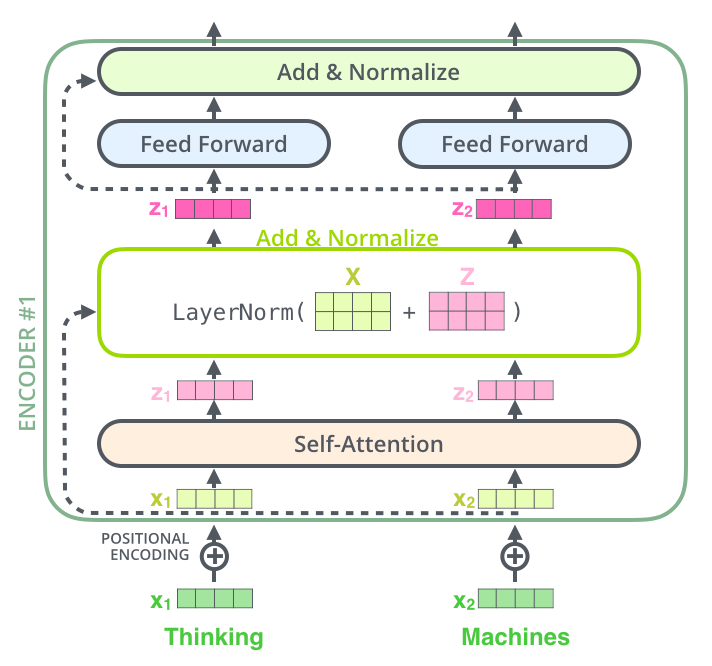
Residuals & LayerNorm
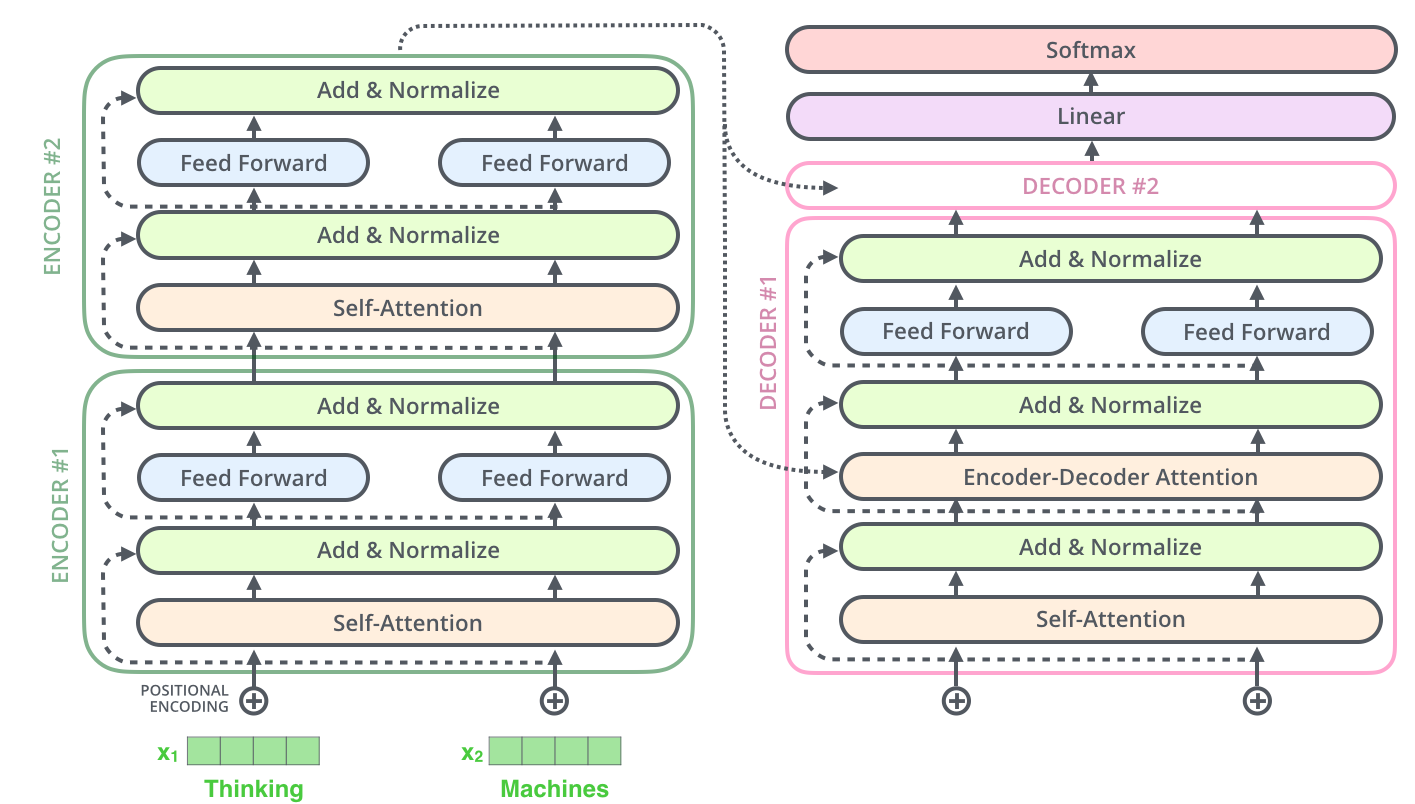
The decoder

encoder self-attn
The decoder


encoder self-attn
The decoder


encoder self-attn
decoder self-attn (masked)

The decoder


encoder self-attn
decoder self-attn (masked)

- Mask subsequent positions (before softmax)
scores.masked_fill_(~mask, float('-inf'))- In PyTorch
The decoder



encoder self-attn
context attention
decoder self-attn (masked)

The decoder



encoder self-attn
context attention
- Use the encoder output as keys and values
$$\mathbf{S} = \mathrm{score}(\mathbf{Q}, \mathbf{R}_{enc}) \in \mathbb{R}^{m \times n} $$
$$\mathbf{P} = \pi(\mathbf{S}) \in \triangle^{m \times n} $$
$$\mathbf{Z} = \mathbf{P} \mathbf{R}_{enc} \in \mathbb{R}^{m \times d}$$
decoder self-attn (masked)
$$\mathbf{R}_{enc} = \mathrm{Encoder}(\mathbf{x}) \in \mathbb{R}^{n \times d} $$
The decoder
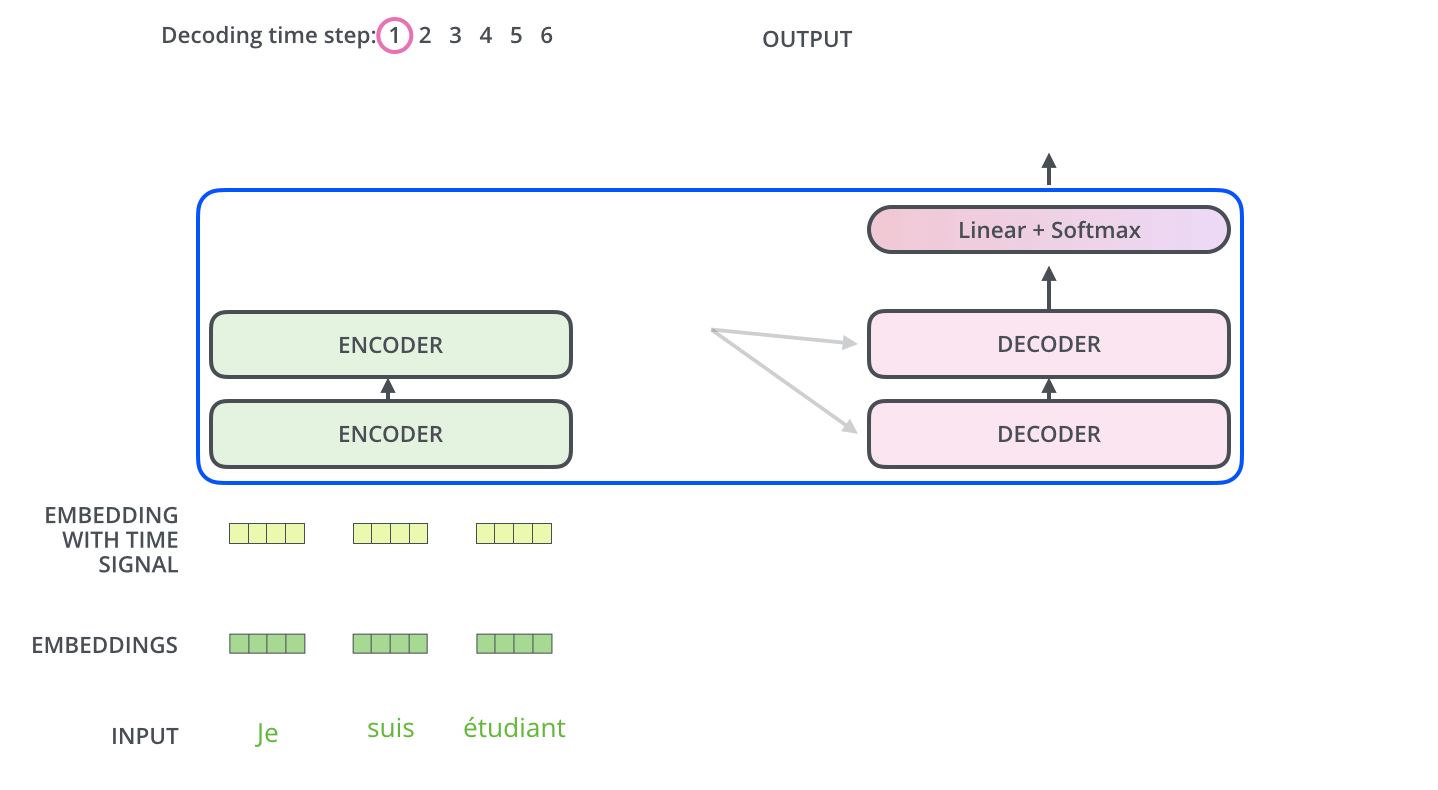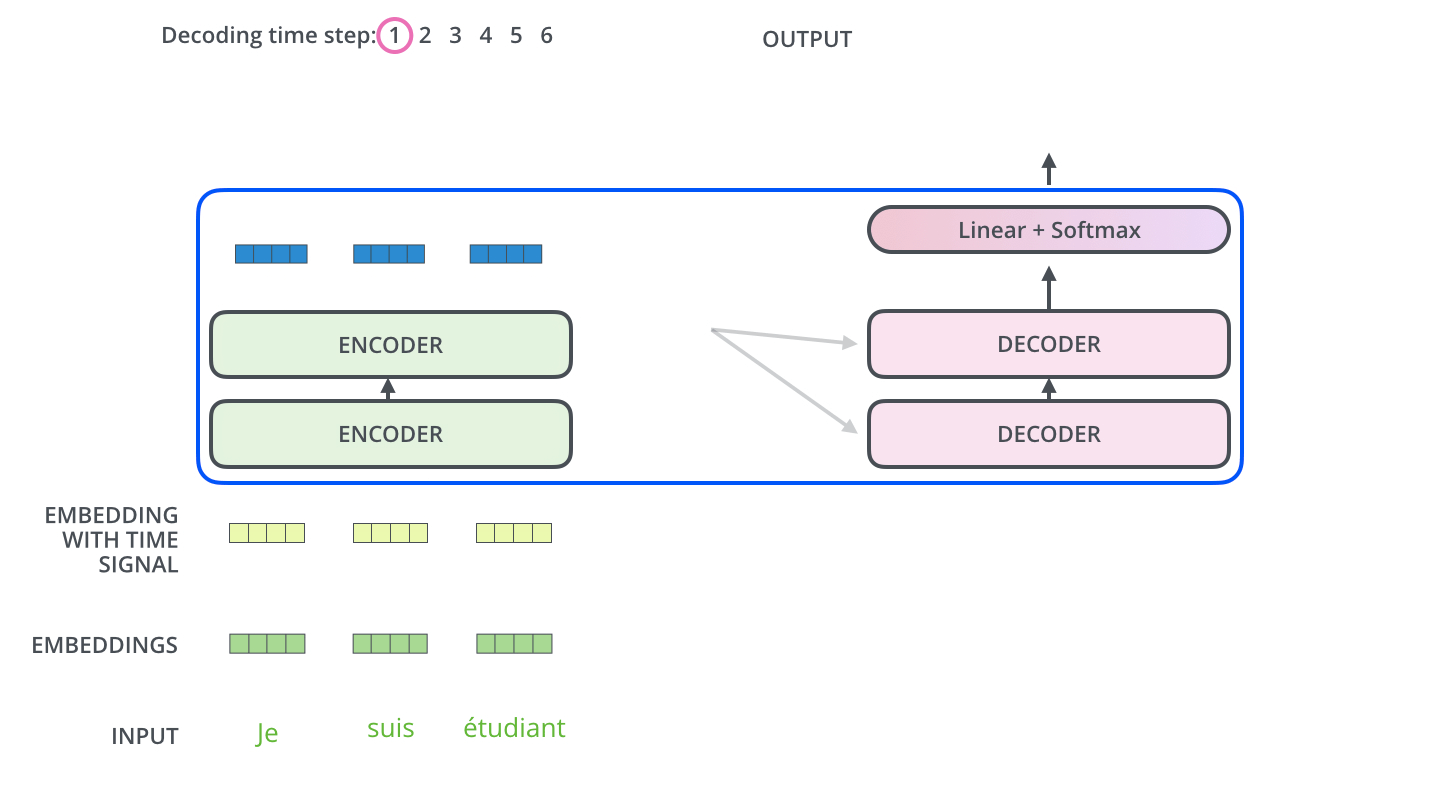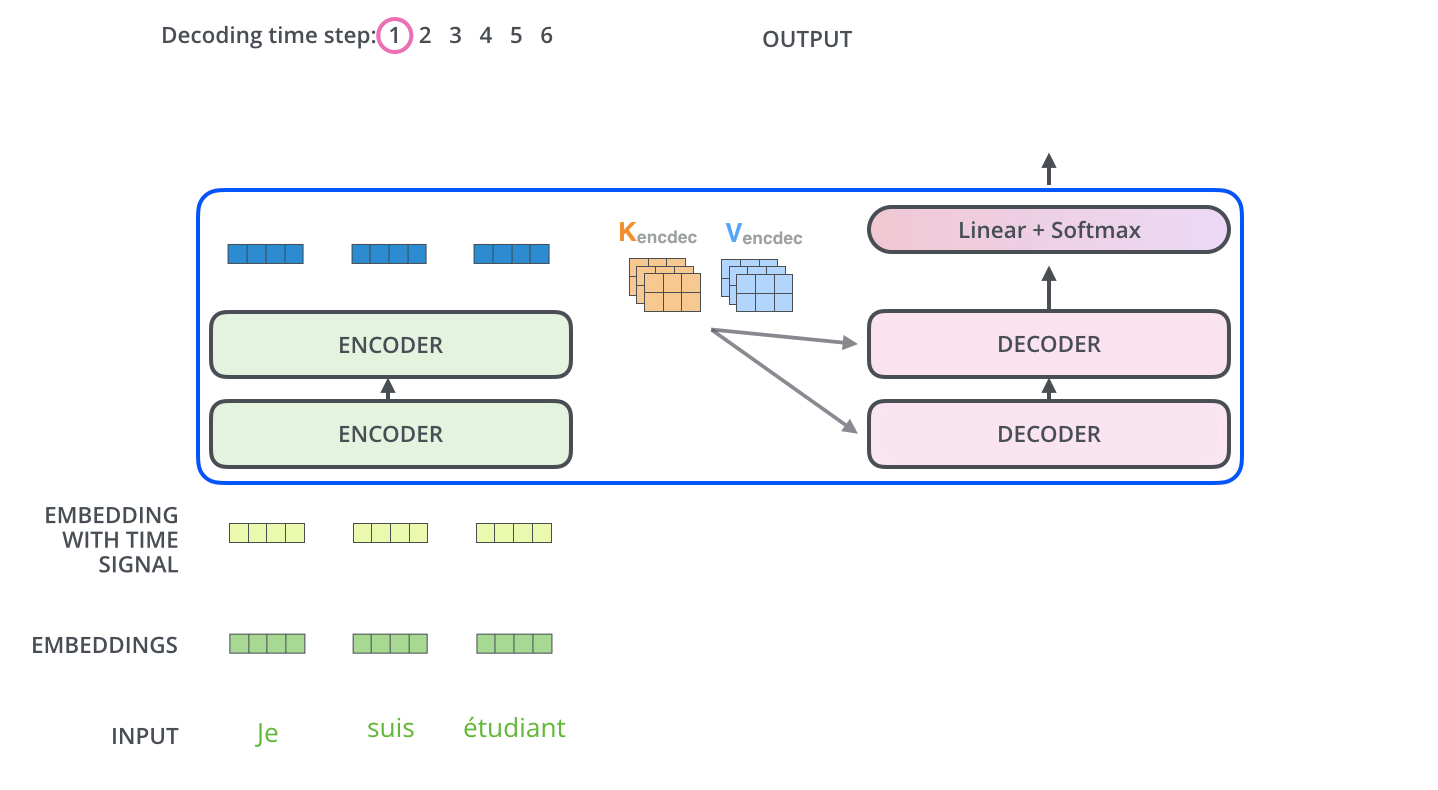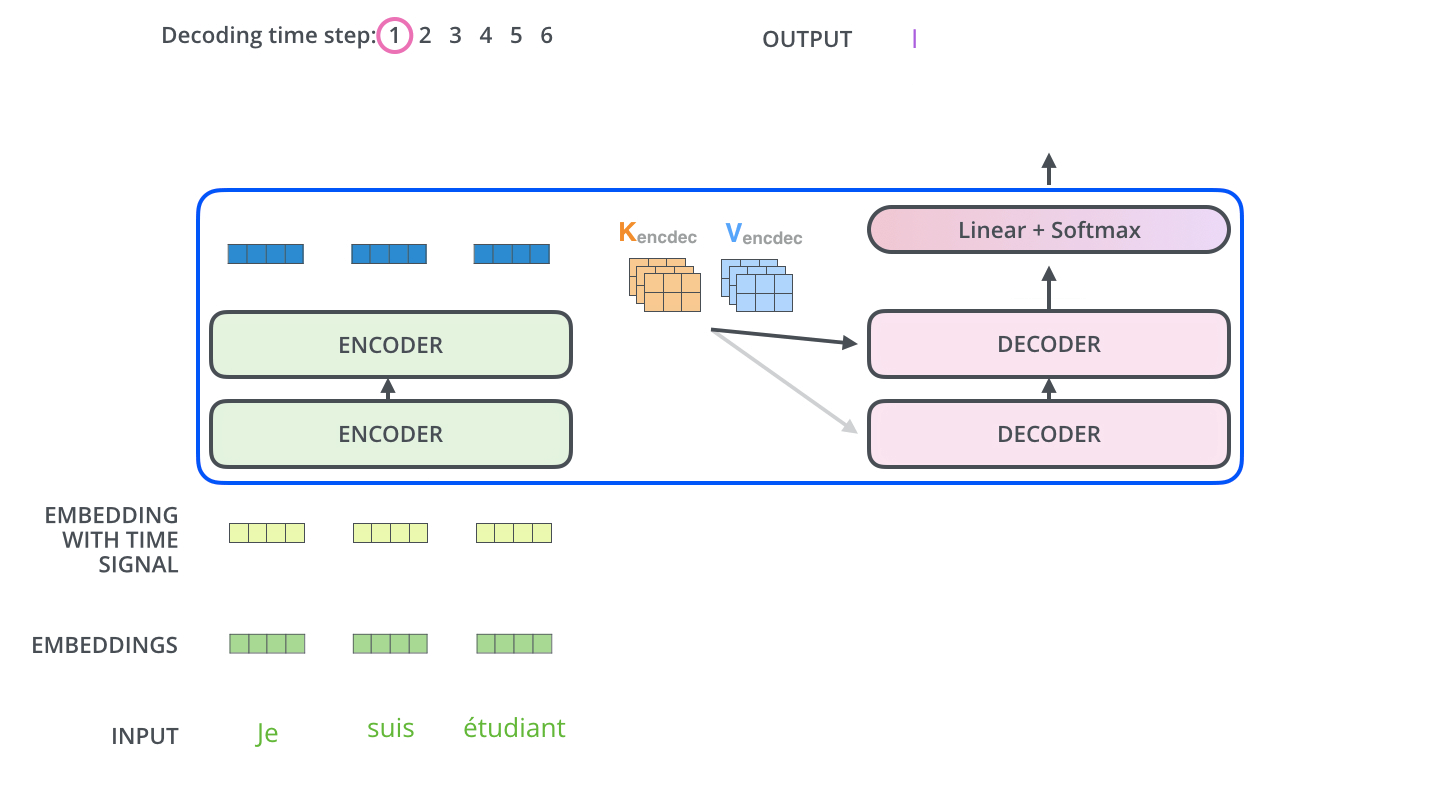
The decoder
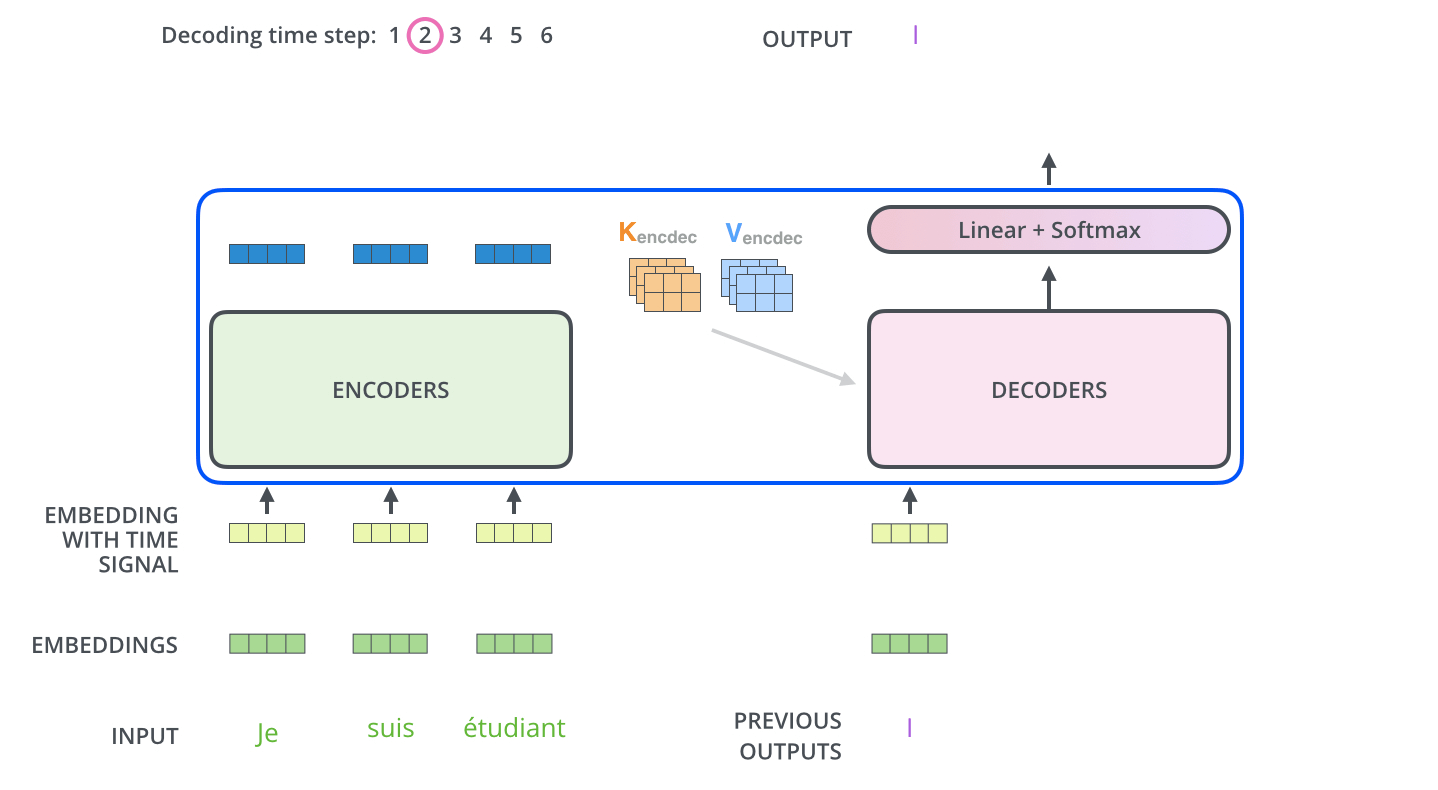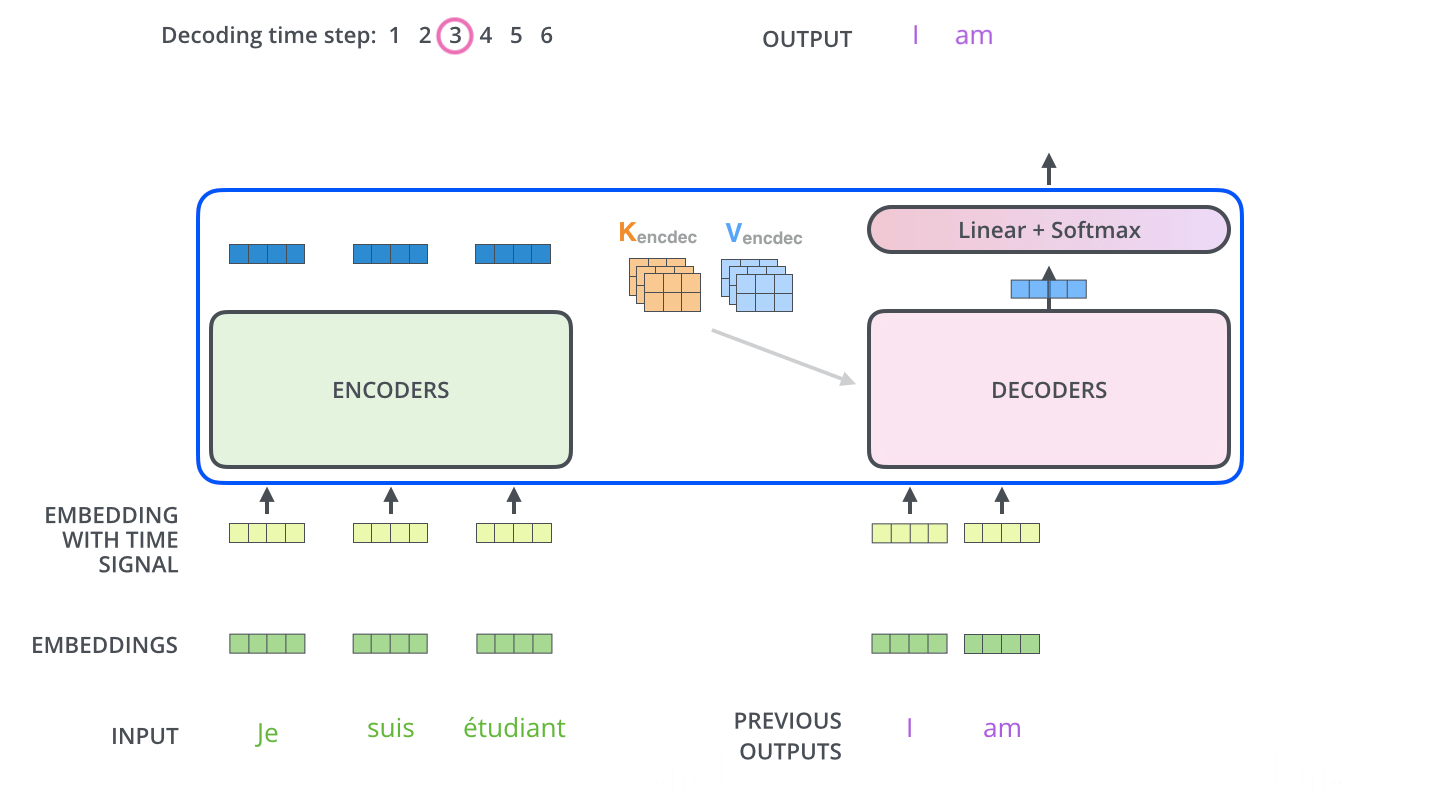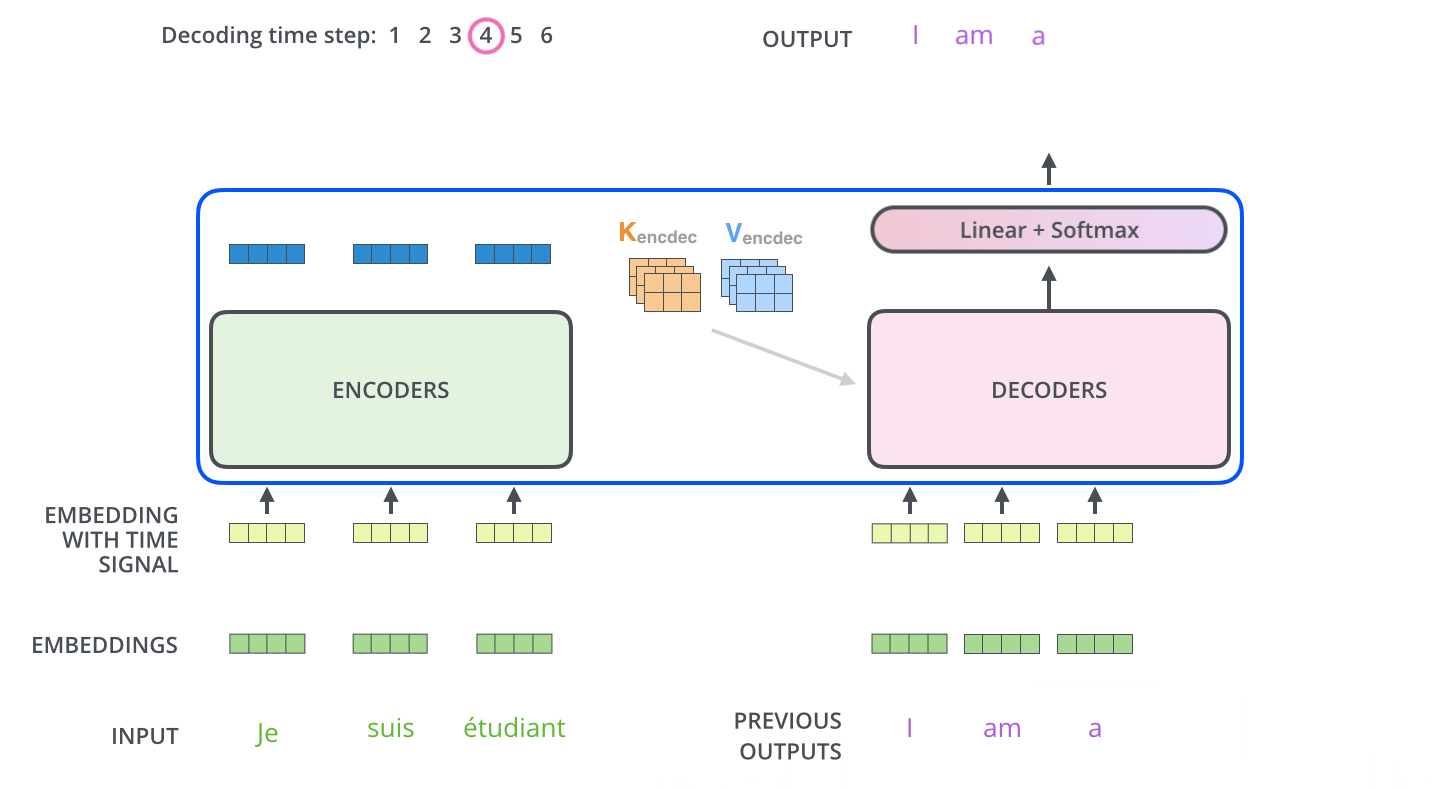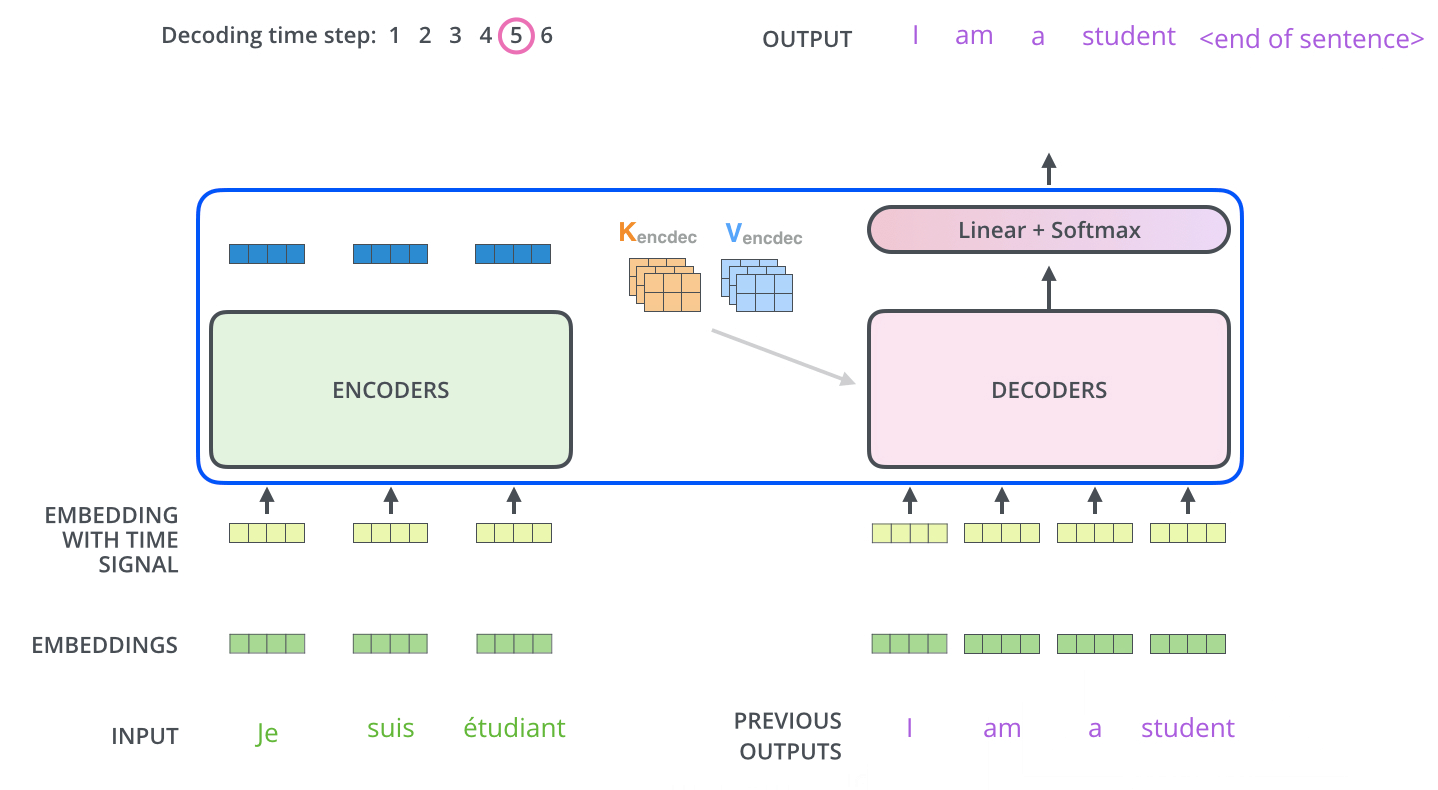
Computational cost

\(n\) = seq. length \(d\) = hidden dim \(k\) = kernel size
Other tricks 🔮
- Training Transformers is like black-magic. There are a bunch of other tricks:
- Label smoothing
- Dropout at every layer before residuals
- Beam search with length penalty
- Subword units - BPEs
- Adam optimizer with learning-rate decay
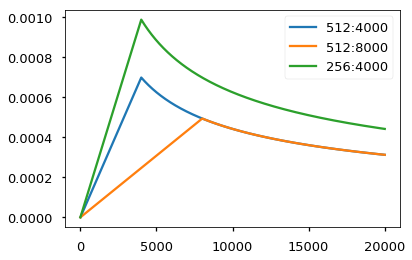
Replacing recurrence
- Self‐attention is the only place where positions interact
- What do we gain over RNN‐based models?
- What do we lose?
Coding & training tips
- Sasha Rush's post is a really good starting point:
http://nlp.seas.harvard.edu/2018/04/03/attention.html
- OpenNMT-py implementation:
encoder part | decoder part
on the "good" order of LayerNorm and Residuals
- PyTorch has a built-in implementation since August, 2019
torch.nn.Transformer
- Training Tips for the Transformer Model
https://arxiv.org/pdf/1804.00247
What else?
- BERT uses only the encoder side (Devlin et al., 2018)
- GPT-3 uses only the decoder side (Brown et al., 2020)
- Absolute vs relative positional encoding (Shaw et al., 2018)
- Use previous encoded states as memory
- Transformer-XL (Dai et al., 2019)
- Compressive Transformer (Rae et al., 2019)
- Induce sparsity
- Sparse Transformer (Child et al., 2019)
- Span Transformer (Sukhbaatar et al., 2019)
- Adap. Sparse Transformer (Correia et al., 2019)
learn an \(\alpha\) in entmax for each head:
Subquadratic self-attention
🔥 very active research topic! why?
+🚀 -💾 ⟹ -💰 +🚀 -💾 ⟹ +🌱
$$O(n^2) \quad \dots \quad O(n\log n) \quad \dots \quad O(n)$$
Subquadratic self-attention

Subquadratic self-attention

Subquadratic self-attention

Subquadratic self-attention

High Performance NLP - EMNLP 2020 (Ilharco et al., 2020)
Pause
🚰
Attention interpretability
🦕 an early example in NLP: alignments ⇄ attention

Attention interpretability
-
What is explainability? interpretability? transparency?
- See this recent work: (Verma et al., 2020)
- See Explainable AI Tutorial - AAAI 2020
- What is the overall goal of the explanation by attention?
expose which tokens are the most important ones for a particular prediction => saliency map
-
To whom are we explaining?
👶👶 Non-experts
👩💼👨💼 Investors
👩💻👨💻 Model developers
Attention debate

BiLSTM with attention - basic architecture for text classification tasks
Attention is not explanation
- Do attention weights correlate with gradient and leave-one-out measures?
Gradient:
Leave-one-out:
$$\nabla_{\mathbf{x}_i} f(\mathbf{x}_{1:n}) \cdot \mathbf{x}_i$$
- First-order Taylor expansion near \(\mathbf{x}_i\)
- Linear model: gradient=coefficients
- First-order Taylor expansion near \(\mathbf{x}_i\)
- Linear model: gradient=coefficients
$$ f(\mathbf{x}_{1:n}) - f(\mathbf{x}_{-i})$$
Attention is not explanation
- Do attention weights correlate with gradient and leave-one-out measures? No!

Attention is not explanation
- Do attention weights correlate with gradient and leave-one-out measures? No!
- Can we find alternative attention distributions \(\tilde{\alpha}\) that yield the same prediction as the original \(\alpha^\star\)?
Adversarial attention:
$$\max_{\tilde{\alpha} \in \triangle^n} f_{\tilde{\alpha}}(\mathbf{x}_{1:n})$$
$$\mathrm{s.t.} \quad |f_{\tilde{\alpha}(\mathbf{x}_{1:n})} - f_{\alpha^\star}(\mathbf{x}_{1:n})| < \epsilon$$
Attention is not explanation
- Do attention weights correlate with gradient and leave-one-out measures? No!
- Can we find alternative attention distributions \(\tilde{\alpha}\) that yield the same prediction as the original \(\alpha^\star\)? Yes! Easily!

Is attention interpretable?
- What happens if we erase the highest attention weight and re-normalize the distribution? Does the decision flips?

Is attention interpretable?
- What happens if we erase the highest attention weight and re-normalize the distribution? Does the decision flips? No!


Fraction of original attention weights removed before first decision flip
Is attention interpretable?
- What happens if we erase the highest attention weight and re-normalize the distribution? Does the decision flips? No!


Fraction of original attention weights removed before first decision flip
"the number of zeroed attended items is often too large to be helpful as an explanation"
Learning to deceive
- Setup tasks such that it is known, a priori, which tokens are useful for prediction
- e.g. edit examples of occupation role detection such that "female" tokens would imply a specific label

Learning to deceive
- Train by trying to neglect impermissible tokens \(\mathbf{m}\)
- \(\mathbf{m}_i = 1\) if \(x_i\) is impermissible and \(0\) otherwise
Learning to deceive
- Train by trying to neglect impermissible tokens \(\mathbf{m}\)
- \(\mathbf{m}_i = 1\) if \(x_i\) is impermissible and \(0\) otherwise
Overall, attention can be manipulated with a negligible drop of performance
Learning to deceive
- Train by trying to neglect impermissible tokens \(\mathbf{m}\)
- \(\mathbf{m}_i = 1\) if \(x_i\) is impermissible and \(0\) otherwise
- Models find interesting alternative workarounds!
- RNN-based leak information via recurrent connections
- Embed-based leak information via vector norms
Overall, attention can be manipulated with a negligible drop of performance
Learning to deceive
- RNN-based leak information via recurrent connections
- Embed-based leak information via vector norms

Attention is not not explanation
- Questions the conclusions of the previous papers and proposes various explainability tests
- Incomplete adversarial attention experiment
- Plausible vs faithful explanation
"we hold that attention scores are used as providing an explanation; not the explanation."
"Jain and Wallace provide alternative distributions which may result in similar predictions, but [...] (ignore the) fact that the model was trained to attend to the tokens it chose"
Attention is not not explanation
"Train an adversary that minimizes change in prediction scores, while maximizing changes in the learned attention distributions "
Attention is not not explanation
"Train an adversary that minimizes change in prediction scores, while maximizing changes in the learned attention distributions "


Attention is not not explanation
"Train an adversary that minimizes change in prediction scores, while maximizing changes in the learned attention distributions "


😄 🙁
Attention is not not explanation
- Plausible vs faithful explanation
- Plausibility: how convincing the explanation is to humans 🤓
-
Faithfulness: how accurately it reflects the true reasoning process of the model 🤖
- For attention to be faithful, it should:
- Be necessary
- Hard to manipulate
- Work out of contextualized setting
- Attention is not causation:
- "attention is not explanation by definition, if a causal explanation is assumed" <===> faithfulness
Towards faithful models?
- Graded notion of faithfulness
- An entire faithful explanation might be impossible
- Instead, consider the scale of faithfulness
Towards faithful models?
- Graded notion of faithfulness
- An entire faithful explanation might be impossible
- Instead, consider the scale of faithfulness
-
Rudin (2018) defines explainability as a plausible (but not necessarily faithful) reconstruction of the decision-making process
- Riedl (2019) argues that explainability mimics what humans do when rationalizing past actions

Plausibility is also important 🤓
- "Do you believe that highlighted tokens capture the model’s prediction?"
- Manipulated attentions received a much lower rating than non-manipulated ones
- Attention from BiRNN are very similar to human's attentions (for all evaluated metrics)
- But as length increases, they become less similar
- But as length increases, they become less similar
- For text classification, humans find attention explanations informative enough to correct predictions
- But not for natural language inference
Perhaps, we can ask more
- Should attention weights correlate with erasure and gradient measures?
- Can we regard them as groundtruth for explainability?
- Are they reliable? (Kindermans et al., 2017)
- Are we evaluating on the right task?
- Attention is a key piece in tasks like MT and ASR!
- Attention is a key piece in tasks like MT and ASR!
- Are we analyzing the right models?
- What if we limit/increase the contextualization?
- What if we have latent variables?
- What are the mechanisms that affect interpretability?
Circumventing attention issues
- Contextualized hidden vectors are very similar

Circumventing attention issues
- Contextualized hidden vectors are very similar

Circumventing attention issues
-
Horizontal issue: contextual vectors leak information
- Vertical issue: hidden states lose information about the original input \(h_i \iff w_i\)
hidden state
word embedding
predicted words
masked words
Circumventing attention issues
- Faithfulness by construction: rationalizers
masked selection!
generator \((\phi)\)
predictor \((\theta)\)
- Encourage compact and contiguous explanations
Circumventing attention issues
- Faithfulness by construction: rationalizers
- Training is done with REINFORCE
- unbiased but high variance estimator
- unbiased but high variance estimator
- HardKuma instead of Bernoulli variables
- reparameterization trick & controlled sparsity
- reparameterization trick & controlled sparsity
- Or... we can use α-entmax as z
lower bound on the log-likelihood
penalties
Interpreting Transformers
-
Probing
- Are linguistic structure encoded in the representations?
-
"Recent" area but growing fast
- Analyzing attention heads
- Analyzing attention flow
- Analyzing token identifiability across layers
Interpreting Transformers
- Specialized head: focus on rare tokens

Interpreting Transformers
- Specialized head: focus on neighbor tokens

Interpreting Transformers
- Specialized head: merge subword units

Interpreting Transformers
- Attention flow: consider the Transformer as a DAG structure: attention in \(\ell=1\) is not the same as in \(\ell > 1\)

-
Vertices are tokens
-
Edges are connections between \(\mathbf{q}_i\) and \(\mathbf{k}_j\)
- Weights are the attention weights \(\alpha\)
Interpreting Transformers
- Attention flow: consider the Transformer as a DAG structure: attention in \(\ell=1\) is not the same as in \(\ell > 1\)

Interpreting Transformers
- Attention flow: which tokens can be ignored as layers go up such that the task performance remains the "same"?

Interpreting Transformers

input gating
Interpreting Transformers

input gating
Q: Where did the broncos practice for the Super Bowl?
---
A: The Panthers used the San Jose State practice facility and stayed at the San Jose Marriott. The Broncos practiced at Stanford University and stayed at the Santa Clara Marriott.
Interpreting Transformers

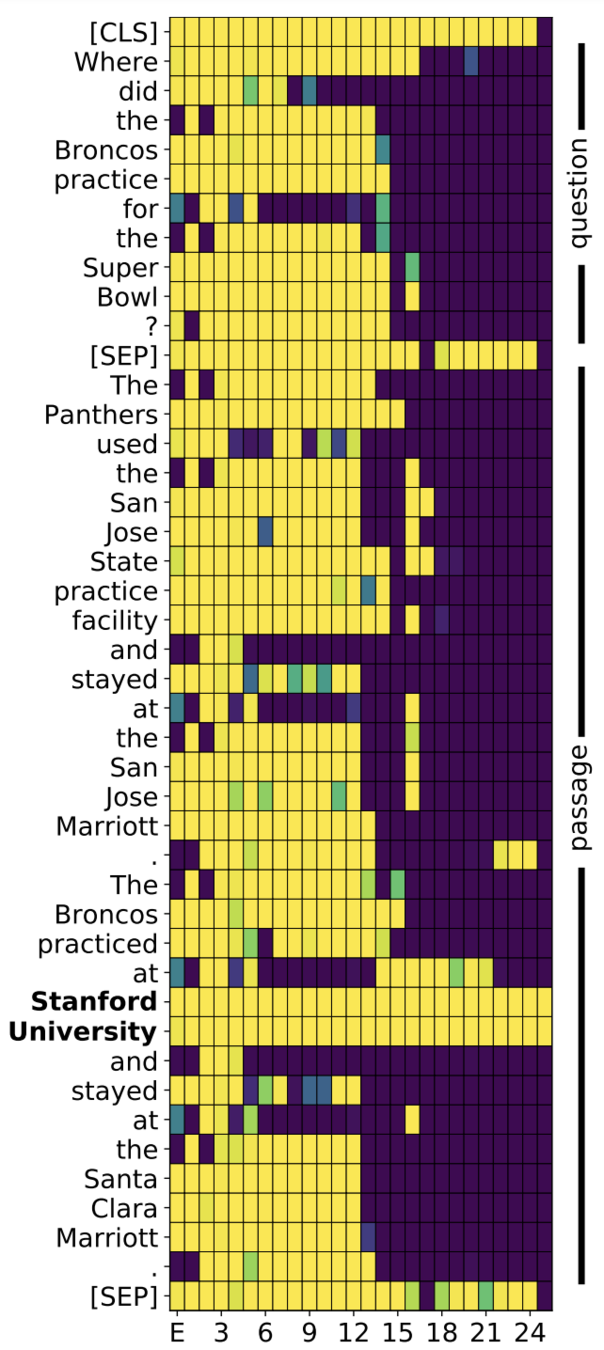
input gating
hidden states gating
Interpreting Transformers


input gating
hidden states gating
special tokens!
Interpreting Transformers
- Analyzing token identifiability across layers

Interpreting Transformers
- Analyzing token identifiability across layers
"when the sequence length is larger than the attention head dimension (\(n > d\)), self-attention is not unique"
Interpreting Transformers
- Hot research area!
- In 2020: Interpretability track for ACL and EMNLP!
- BlackboxNLP workshop:
https://blackboxnlp.github.io/
- There are still many contributions to be made!
Conclusions
- Attention is a key ingredient of neural nets
- Attention has many variants with different advantages
- Transformers are "not" just a bunch of self-attention
- Transformers can be improved in terms of speed and memory
- active research area
- active research area
- Attention plots can be misleading. Make more analysis!
- be careful with attention claims
- active research area
- open debate situation