Learning Space Partitions for Nearest Neighbor Search
Instituto de Telecomunicações
March 17, 2020

Brief look into the future
- Nearest Neighbor Search (NNS) paper
-
Based on space partitions of \(\mathbb{R}^d\)
- Balanced graph partitioning -> supervised classification
- Neural LSH
- Neural LSH
- Outperforms classical NNS methods
- Quantization-based
- Tree-based
- Data-oblivious LSH
Refs
- Alexandr Andoni's presentation:
http://www.cs.columbia.edu/~andoni/similaritySearch_simons.pdf
- Piotr Indyk's presentation:
https://people.csail.mit.edu/indyk/icm18.pdf
- Approximate Nearest Neighbor Search in High Dimensions (Andoni et. al, 2018)
https://arxiv.org/pdf/1806.09823.pdf
- Learning to Hash for Indexing Big Data - A Survey (Wang et al., 2015)
https://arxiv.org/pdf/1509.05472.pdf
Nearest Neighbor Search (NNS)
-
1D case
- \(P \in \mathbb{R}^{n \times 1}\) (dataset)
- query \(q \in \mathbb{R}\)
- Sort the dataset -> binary search!
- O(log n) time
- O(n) memory

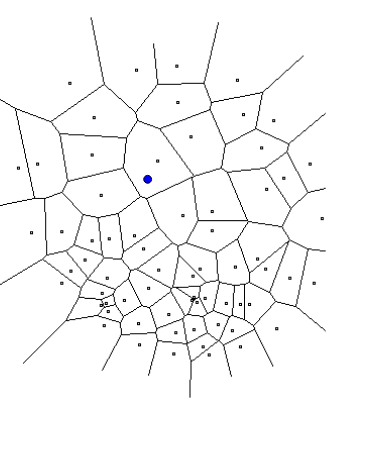
Nearest Neighbor Search (NNS)
-
2D case
- \(P \in \mathbb{R}^{n \times 2}\) (dataset)
- query \(q \in \mathbb{R^2}\)
- Build a Voronoi diagram
- O(log n) time
- O(n) memory
Nearest Neighbor Search (NNS)
-
3+D case
- \(P \in \mathbb{R}^{n \times d}\) (dataset)
- query \(q \in \mathbb{R^d}\)
- Build a Voronoi diagram
- \(n^{⌈d/2⌉}\) edges
- \(O(d + log n)\) time
- \(O(n^d)\) memory

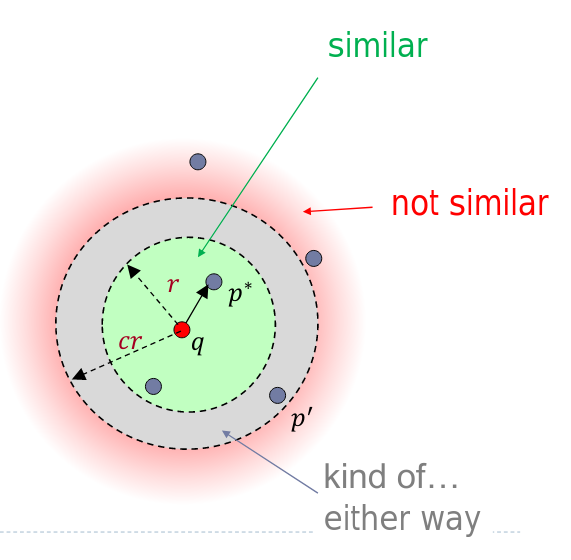
Approximated Near Neighbor Search
-
\((c,r)\)-approximate near neighbor: given a query \(q\), report a point \(p \in P\) s.t. \(||p' - q|| \leq cr\)
-
as long there is some
point within distance \(r\)
-
as long there is some
- Can get the nearest neighbor
\(||p^*-q|| \leq \min_p c||p-q||\)
-
Randomized algorithms:
each point reported with 90%
probability
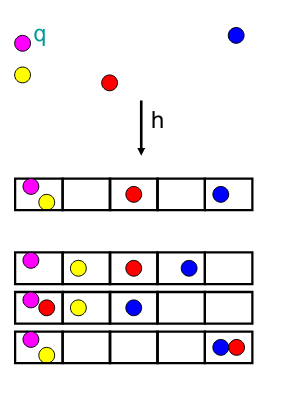
Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)
Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)

Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)

Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)

Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)

The best map
we can have in
terms of time and
memory complexity
\(O(n^{1/c^2})\) time
\(O(n^{1+1/c^2})\) memory
Locality Sensitive Hashing (LSH)
- Map points \(g(p)\) into "codes" s.t. similar points have the same code
- \(\mathrm{Pr}[g(p) = g(q)]\) is high
when \(||p-q|| \leq cr \)
- \(\mathrm{Pr}[g(p') = g(q)]\) is low
when \(||p'-q|| > cr\)
- Space partitions
- LSH (data independent map)
- This paper (data dependent map)

The best map
we can have in
terms of time and
memory complexity
\(O(n^{1/c^2})\) time
\(O(n^{1+1/c^2})\) memory
This paper (Neural LSH)
- Given:
- Dataset \(P \in \mathbb{R}^{n \times d}\)
-
\(m\) bins
- The goal is to find a partition \(\mathcal{R} \in \mathbb{R}^d\) into \(m\) bins
- Balanced: \(|\mathcal{R}| \approx n/m\)
- Locality sensitive: \( q \in \mathbb{R}^d, m_{q} \approx m_{\mathcal{N}(q)} \)
- Simple: the point location alg. should be efficient
Formulation
\min\limits_{\mathcal{R}} \, \mathbb{E}_q \Big[\sum_{p \in N_k(q)} [[\mathcal{R}(p) \neq \mathcal{R}(q)]] \Big]
\mathrm{s.t.} \qquad \forall_{p \in P} |\mathcal{R}(p)| \leq (1+\eta)\dfrac{n}{m}
\(q\) is sampled from the query distribution
\(N_k(q)\) is the set of \(k\) nearest neighbors of \(q\)
\(\eta\) is a balance parameter
\(\mathcal{R}(p)\) is the partition of \(P\) that contains \(p\)
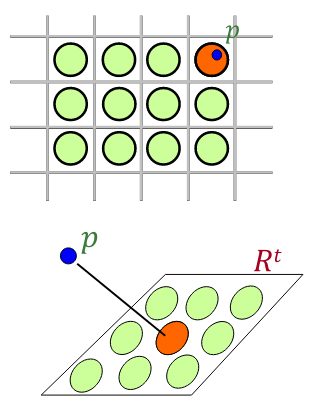
Building a graph
- Suppose that the query is sampled from the dataset \(q \sim P\)
- Let \(G\) be the \(k\)-NN graph
- each vertex is a data point \(p \in P\)
- edges connect nearest neighbors of \(p\)
- \(\implies\) partition vertices of \(G\) into \(m\) bins, such that
- each bin has roughly \(n/m\) vertices
- number of edges crossing bins is small as possible
Building a graph
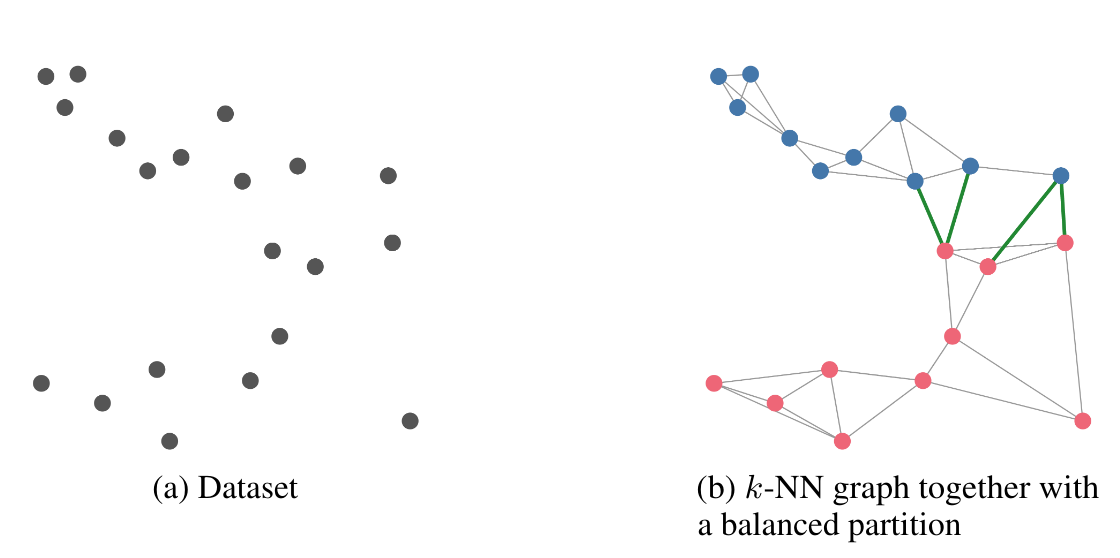
Learning partitions
- Suppose that the query is not sampled from the dataset:
- \( q \notin P \)
- \( q \notin P \)
- We need to extend the partition \(\tilde{\mathcal{R}}\) of \(G\) to a partition \(\mathcal{R}\) of the whole space \(\mathbb{R}^d\)
- Learn a partition in a supervised way:
- \(y_i = m_{\tilde{\mathcal{R}}(p_i)}\)
- \(\mathcal{R}(p) := f(p_i) \approx y_i \)
- \(f\) can be any classifier
Learning partitions
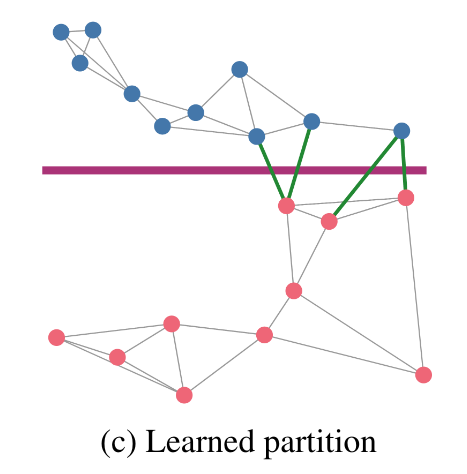
More ideas
-
Hierarchical partitions: If the number of bins \(m\) is large
- Create partitions recursively
-
Multi-probe querying: predict several bins!
- e.g. top-k softmax
- e.g. top-k softmax
- Soft labels: infer a probability distribution over bins
\(\mathcal{P} = (p_1, p_2, ..., p_m)\)
\(\mathcal{Q} = (q_1, q_2, ..., q_m)\)
\(\min D_{KL}(\mathcal{P}||\mathcal{Q})\)
Among \(S\) bins sampled uniformly from \(m_{N(p)} \cup m_p \)
For a point \(p\):
More ideas
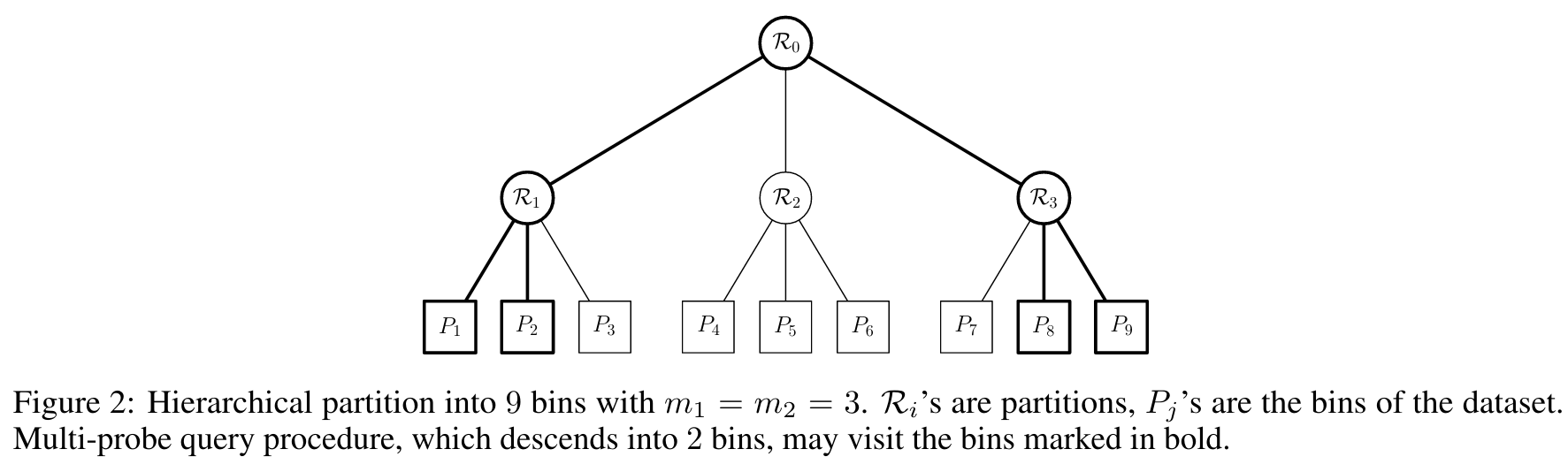

Experiments
- Standard datasets for ANN benchmarks:
- SIFT; Glove embeddings; MNIST
- SIFT; Glove embeddings; MNIST
- Metrics:
- top-k accuracy
- average number of candidates
- 0.95th quantile of the number of candidates
- Methods:
- Neural LSH: small neural net (3x512 and 2x390)
- Regression LSH: logistic regression
Results - neural net
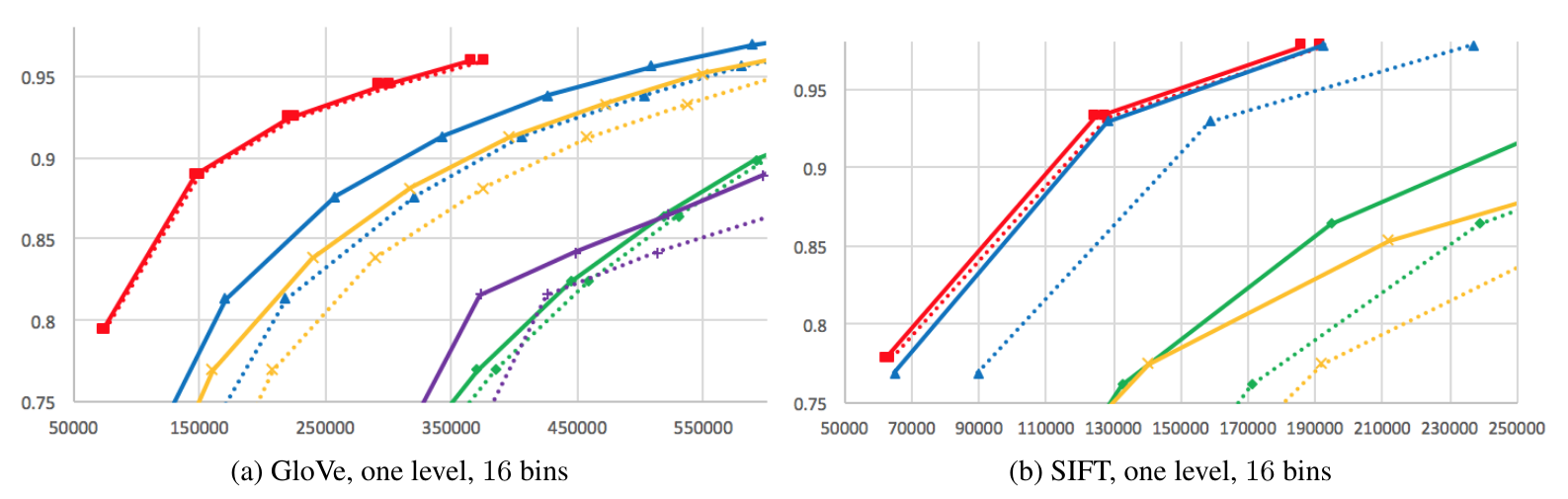
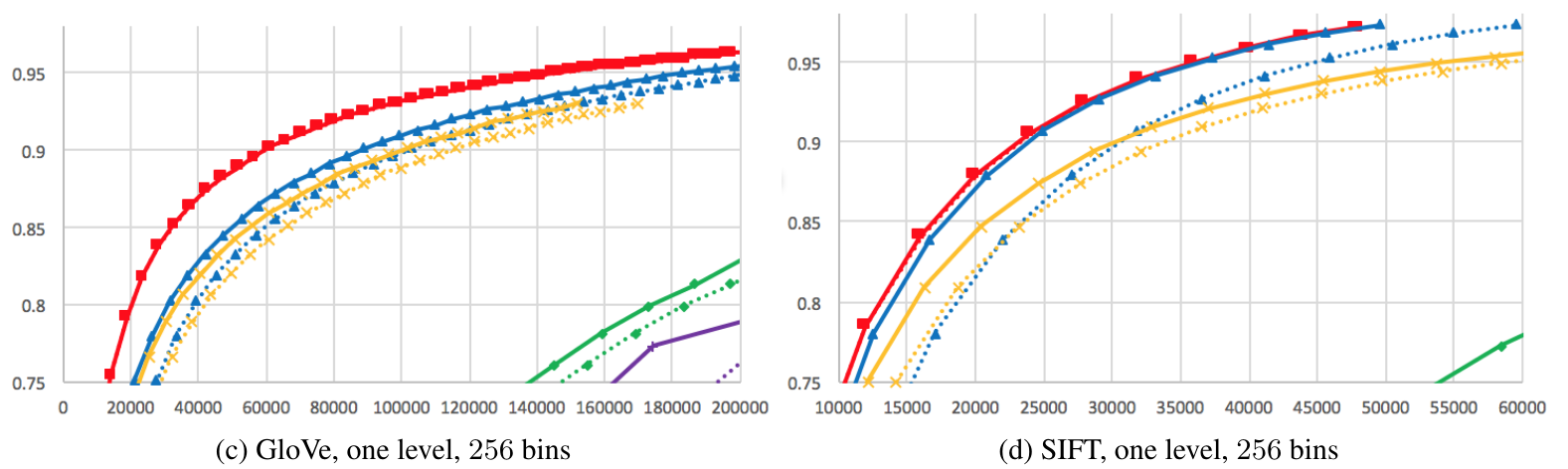
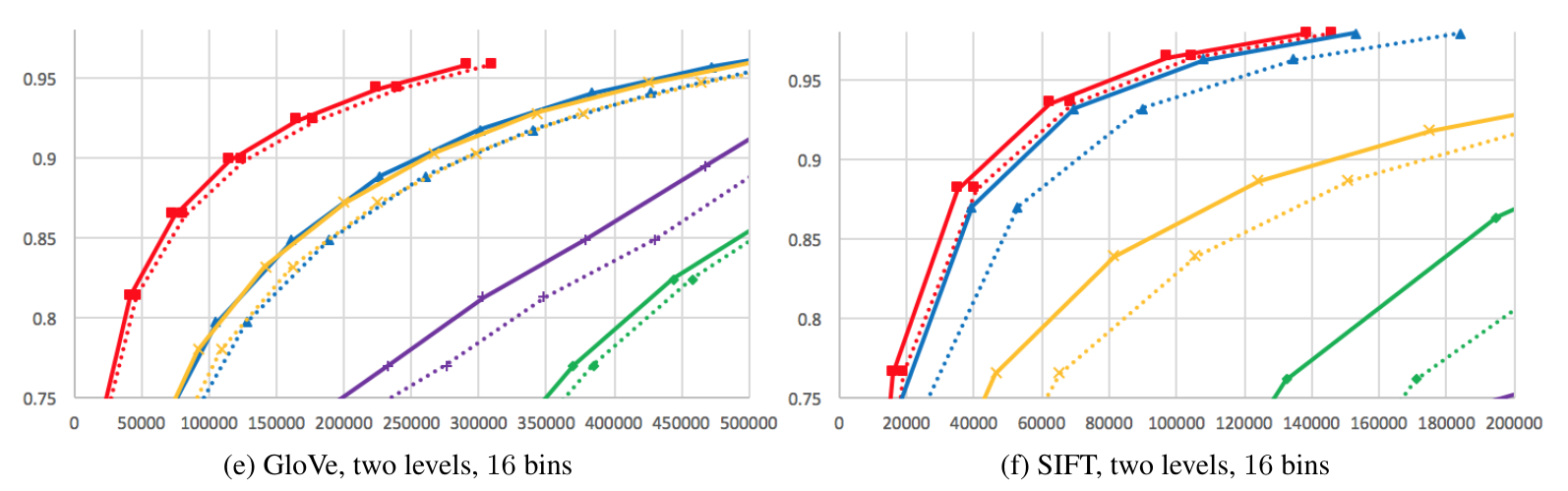
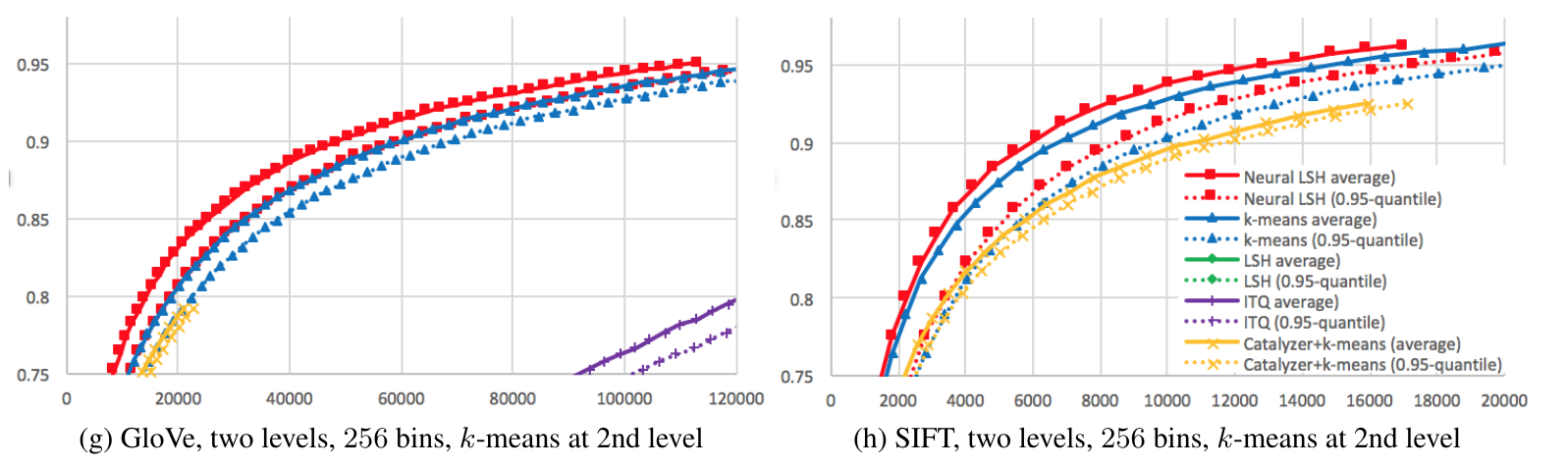
Results - neural net




Results - linear classifier
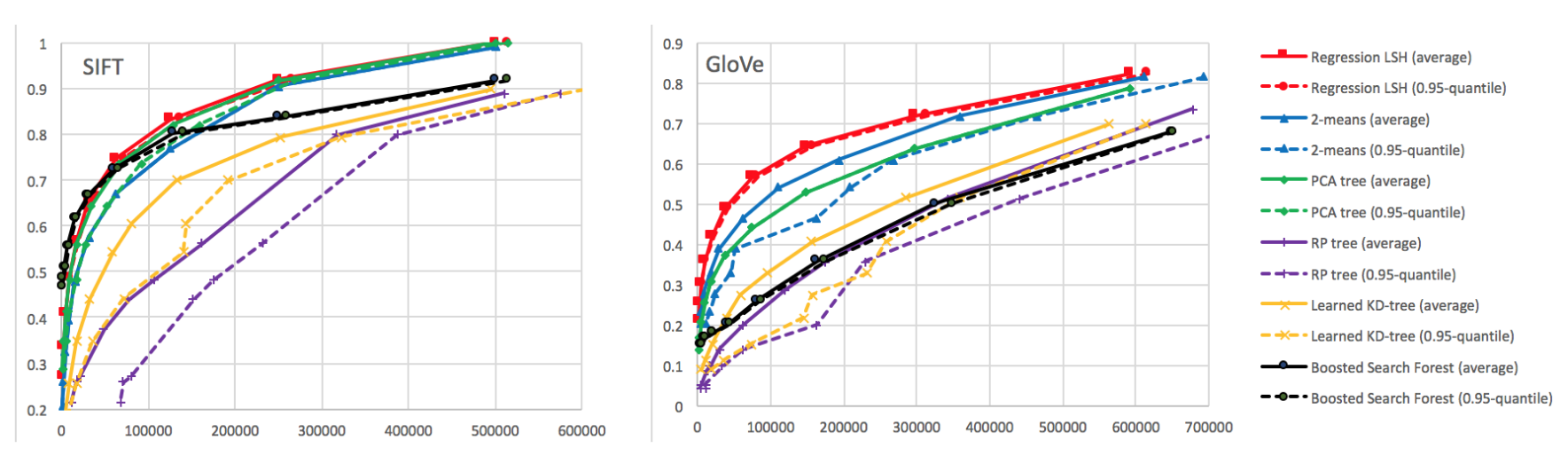

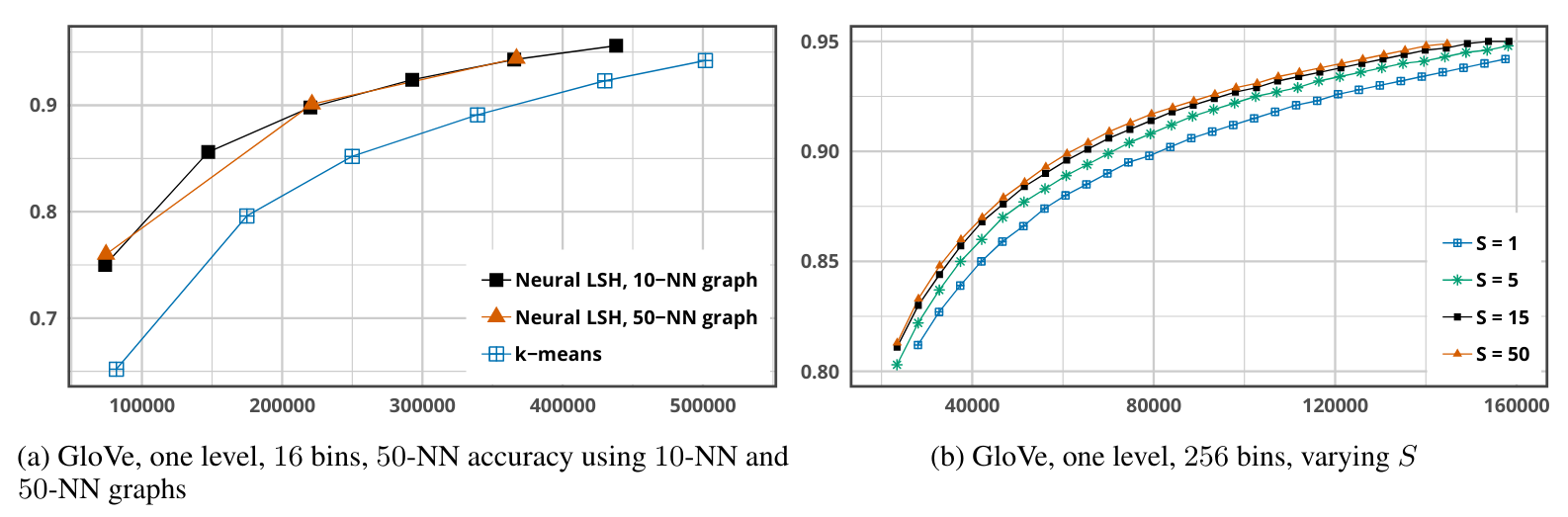
Results - hyperparams

Future ideas
- Other distances
- Edit distance
- Earth mover's distance
- Jointly optimize the graph partitioning & classifier
- What about graph-indexing based on neural nets?
- “continuous” sparsemax?