Predicting Attention Sparsity

in Transformers

May 27, 2022

Marcos Treviso

António Góis

Patrick Fernandes

Erick Fonseca

André F. T. Martins

DEEPSPIN

Interpretable heads

softmax transformer
(Voita et al., 2019)

rare tokens

Interpretable heads

softmax transformer
(Voita et al., 2019)

α-entmax transformer
(Correia et al., 2019)

rare tokens

neighboring tokens

Interpretable heads

softmax transformer
(Voita et al., 2019)

α-entmax transformer
(Correia et al., 2019)

rare tokens

neighboring tokens

both are $\mathcal{O}(n^2)$

Interpretable heads

softmax transformer
(Voita et al., 2019)

α-entmax transformer
(Correia et al., 2019)

rare tokens

neighboring tokens

can we save

computation?

$$O(n^2) \dots O(n) \dots O(1)$$

both are $\mathcal{O}(n^2)$

Subquadratic self-attention

Sparse transformer

Longformer

Subquadratic self-attention

Sparse transformer

Longformer

BigBird

Subquadratic self-attention

Sparse transformer

Longformer

BigBird

Reformer

Subquadratic self-attention

Sparse transformer

Longformer

BigBird

Routing transformer

Reformer

Subquadratic self-attention

Sparse transformer

Longformer

BigBird

Routing transformer

Reformer

Sparsefinder

Sparsefinder

$\mathcal{G}_h$

Sparsefinder

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$

$\bm{k}' = \bm{W}^Q_h \bm{k}$

distance to

negative pairs

distance to

positive pairs

margin

lower
dimensionality

$\mathcal{G}_h$

Sparsefinder

distance-based $\mathcal{O}(n^2)$

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}$

bucketing $\mathcal{O}(n\sqrt{n})$

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid f(\bm{q}'_i) \cap f(\bm{k}'_j) \neq \emptyset\}$

clustering $\mathcal{O}(n\sqrt{n})$

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid c(\bm{q}'_i) = c(\bm{k}'_j) \}$

$f$ yields bucket ids element-wise

$c$ yields a cluster id

$\mathcal{G}_h$

Sparsefinder

$\mathcal{G}_h$

α-entmax graph

• $\mathcal{G}$: gold $\alpha$-entmax graph

• $\hat{\mathcal{G}}$: predicted graph

• $|\mathcal{G}|$: number of edges

e.g.,

$\mathcal{G}$: gold $\alpha$-entmax graph

e.g.,

$\hat{\mathcal{G}}$: predicted graph

α-entmax graph

• $\mathcal{G}$: gold $\alpha$-entmax graph

• $\hat{\mathcal{G}}$: predicted graph

• $|\mathcal{G}|$: number of edges

recall($\mathcal{G}, \hat{\mathcal{G}})$

$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$

recall($\mathcal{G}, \hat{\mathcal{G}})$

$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$

sparse consistency property

if $\mathcal{G} \subseteq \hat{\mathcal{G}}$,

recall($\mathcal{G}, \hat{\mathcal{G}}) = 100\%$

α-entmax graph

• $\mathcal{G}$: gold $\alpha$-entmax graph

• $\hat{\mathcal{G}}$: predicted graph

• $|\mathcal{G}|$: number of edges

recall($\mathcal{G}, \hat{\mathcal{G}})$

$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$

sparsity($\hat{\mathcal{G}})$

$$ 1 - \frac{|\hat{\mathcal{G}}|}{nm} $$

sparse consistency property

if $\mathcal{G} \subseteq \hat{\mathcal{G}}$,

recall($\mathcal{G}, \hat{\mathcal{G}}) = 100\%$

α-entmax graph

• $\mathcal{G}$: gold $\alpha$-entmax graph

• $\hat{\mathcal{G}}$: predicted graph

• $|\mathcal{G}|$: number of edges

recall($\mathcal{G}, \hat{\mathcal{G}})$

$$ \frac{|\mathcal{G} \cap \hat{\mathcal{G}}|}{|\mathcal{G}|} $$

sparsity($\hat{\mathcal{G}})$

$$ 1 - \frac{|\hat{\mathcal{G}}|}{nm} $$

sparse consistency property

if $\mathcal{G} \subseteq \hat{\mathcal{G}}$,

recall($\mathcal{G}, \hat{\mathcal{G}}) = 100\%$

efficiency

as sparsity($\hat{\mathcal{G}}$) $\to 1$,

save computation (theoretically)

α-entmax graph

• $\mathcal{G}$: gold $\alpha$-entmax graph

• $\hat{\mathcal{G}}$: predicted graph

• $|\mathcal{G}|$: number of edges

Experiments: MT and MLM

• MT: Transformer trained on IWSLT 2017 with $\alpha=1.5$

• MLM: RoBERTa finetuned on WikiText-103 with $\alpha=1.5$

• Evaluation: replace softmax attention by the approximation at test time

Experiments: MT and MLM

• MT: Transformer trained on IWSLT 2017 with $\alpha=1.5$

• MLM: RoBERTa finetuned on WikiText-103 with $\alpha=1.5$

• Evaluation: replace softmax attention by the approximation at test time

• Compare all methods with Pareto curves

- window size ∈ {0, 1, 3, 5, ..., 27}

- distance threshold ∈ {0.5, 1.0, 1.5, ..., 5.0}

- num. of buckets / clusters ∈ {2, 4, 6, ..., 20}

- num. of random blocks / global tokens ∈ {2, 4, 6, ..., 20}

Experiments: MT

EN→FR

Experiments: MT

EN→FR

Experiments: MT

EN→FR

Experiments: MT

EN→FR

Experiments: MT

EN→FR

Experiments: MT

EN→FR

EN→DE

Experiments: MT

• Attention head example

Ground-truth

Experiments: MT

• Attention head example

Sparsefinder k-means

Experiments: MT

• Attention head example

After applying 1.5-entmax

Experiments: Masked LM

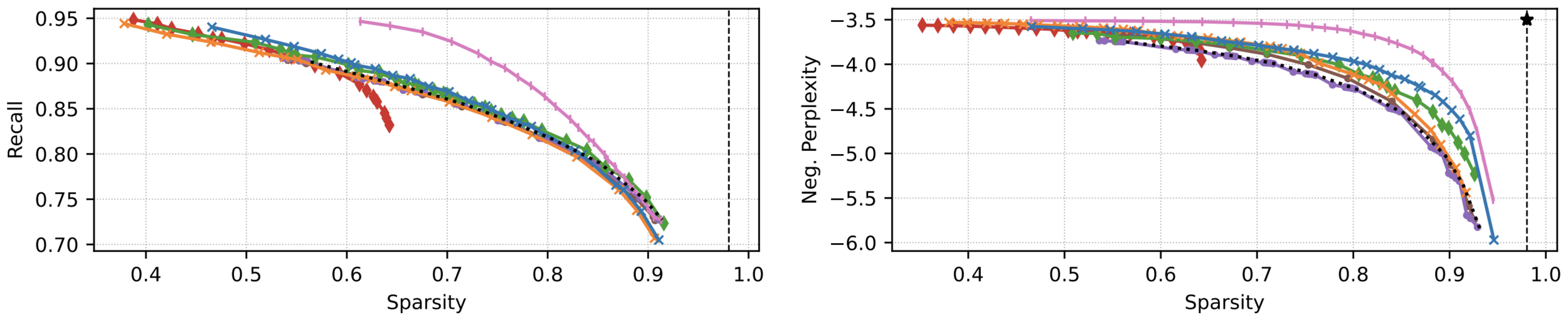
Experiments: Masked LM

• Attention head focusing on coreference tokens

Efficient Sparsefinder

• Learn projections of contiguous-chunked tokens: blocks!

Efficient Sparsefinder

• Learn projections of contiguous-chunked tokens: blocks!

• Resembles BigBird but random pattern is replaced by clustering

v1: top-k queries and keys closest to each centroid

v2: top-k queries for each clusters x top-k keys for each cluster

k = number of attended blocks

window size = 3

Efficient Sparsefinder

• Learn projections of contiguous-chunked tokens: blocks!

• Resembles BigBird but random pattern is replaced by clustering

v1: top-k queries and keys closest to each centroid

v2: top-k queries for each clusters x top-k keys for each cluster

k = number of attended blocks

window size = 3

Efficient Sparsefinder

• Learn projections of contiguous-chunked tokens: blocks!

• Resembles BigBird but random pattern is replaced by clustering

v1: top-k queries and keys closest to each centroid

v2: top-k queries for each clusters x top-k keys for each cluster

k = number of attended blocks

window size = 3

Final Remarks

Taxonomy of Efficient Transformer Architectures by (Tay et al., 2020)

Final Remarks

Taxonomy of Efficient Transformer Architectures by (Tay et al., 2020)

Sparsefinder

Final Remarks

• Avoid the full computation of the score matrix

- distance-based

- bucketing

- clustering

Final Remarks

• Avoid the full computation of the score matrix

- distance-based

- bucketing

- clustering

• Favorable sparsity-recall and sparsity-accuracy tradeoff curves

• Attention heads can remain interpretable

Final Remarks

• Avoid the full computation of the score matrix

- distance-based

- bucketing

- clustering

• Favorable sparsity-recall and sparsity-accuracy tradeoff curves

• Attention heads can remain interpretable

• Lower bound for computational sparsity

Thank you for your

attention!

Questions?

Quadratic self-attention

• Bottleneck in transformers:

...

1 2 3 4 n

$\to \mathcal{O}(n^2)$

Quadratic self-attention

$$O(n^2) \quad \dots \quad O(n\log n) \quad \dots \quad O(n)$$

• Bottleneck in transformers:

...

1 2 3 4 n

$\to \mathcal{O}(n^2)$

       -💰

+🚀 -💾                
       +🌱

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

margin

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

3️⃣ Group $\langle\bm{q},\bm{k}\rangle$ and compute attention within groups

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

margin

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

3️⃣ Group $\langle\bm{q},\bm{k}\rangle$ and compute attention within groups

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

distance-based

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}$

$\mathcal{O}(n^2)$

margin

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

3️⃣ Group $\langle\bm{q},\bm{k}\rangle$ and compute attention within groups

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

distance-based

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}$

$\mathcal{O}(n^2)$

bucketing

quantize each $1,...,r$ dim.
into $\beta$ bins of size $\lceil n/\beta\rceil$

$\mathcal{O}(n\sqrt{n})$

margin

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

3️⃣ Group $\langle\bm{q},\bm{k}\rangle$ and compute attention within groups

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

distance-based

$\hat{\mathcal{G}}_h = \{(\bm{q}_i, \bm{k}_j) \mid \|\bm{q}'_i - \bm{k}'_j\| \leq t\}$

$\mathcal{O}(n^2)$

bucketing

quantize each $1,...,r$ dim.
into $\beta$ bins of size $\lceil n/\beta\rceil$

$\mathcal{O}(n\sqrt{n})$

clustering

learn centroids ${\bm{c}_1, ..., \bm{c}_B}$ and set points to closest cluster

$\mathcal{O}(n\sqrt{n})$

margin

Sparsefinder

1️⃣ Extract heads from a pre-trained $\alpha$-entmax transformer

2️⃣ Learn lower dimensionality projections

3️⃣ Group $\langle\bm{q},\bm{k}\rangle$ and compute attention within groups

4️⃣ Add window and global patterns to $\hat{\mathcal{G}}$

\mathcal{L}_\theta(\mathcal{G}_h) = \Big[ \omega + \|\bm{q}' - \bm{k}'_{\text{P}}\|^2_2 - \|\bm{q}' - \bm{k}'_{\text{N}}\|^2_2 \Big]_{+}

$\bm{q}' = \bm{W}^Q_h \bm{q}$
$\bm{k}' = \bm{W}^Q_h \bm{k}$

negative pair

positive pair

distance-based

bucketing

clustering

margin

Sparse-consistency property

$QK^\top$ scores

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

Sparse-consistency property

$QK^\top$ scores

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$QK^\top$ scores

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

$QK^\top$ scores

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

$QK^\top$ scores

Sparse-consistency property

$\alpha$-entmax

$\Bigg($

$\Bigg)$

$\mathcal{G}$: $\alpha$-entmax attention graph

$QK^\top$ scores

Experiments: Masked LM

• Distribution of part-of-speech tags on the validation set

- for each cluster

- for each head

Experiments: Masked LM

• Distribution of part-of-speech tags on the validation set

- for each cluster

- for each head

• verbs, nouns, auxiliary verbs attend to each other

Sparsefinder cost

$N = $ sequence length
$C = $ number of clusters
$T = \lceil N / C \rceil $ (max-size of balanced clusters)

$O(C \times T^2) = O(C \times N^2 / C^2) = O(N^2 / C)$

If $C = \sqrt{N}$, then

$O(N^2 / C) = O(N\sqrt{N})$

$N = 20 $, $C = 4 $, balanced clusters