The Explanation Game:
Towards Prediction Explainability through Sparse Communication
June 23, 2020



Marcos V. Treviso
André F. T. Martins
- Motivations for Explainability
- Definitions and Works on NLP
- Explainability Techniques and Classic Feature Selection
- Embedded Sparse Attention
- Explainability as Communication
- Experiments
- Human Evaluation
- Final Remarks
Agenda
Social Motivation: Critical Systems

Social Motivation: Critical Systems

Social Motivation: Critical Systems

- Standard ML models have lower precision to detect pedestrians crossing the road if they have dark skin [Wilson et al., 2019]
Social Motivation: Criminal Justice


Social Motivati


on: Criminal Justice
Social Motivation: Imagine
-
Military
-
Drones carrying explosives or weapons
-
Drones carrying explosives or weapons
- Recruiting
- ML models to streamline the process
-
Healthcare
- Responsibility?
- Confidentiality?



Insights Motivation
-
The Deep Patient case (Miotto et al., 2016)
- 700,000 patients / 78 diseases
- DL model with high accuracy for several diseases


Electronic Health Records

Insights Motivation
-
The Deep Patient case (Miotto et al., 2016)
- 700,000 patients / 78 diseases
- DL model with high accuracy for several diseases
- But doctors find very hard to antecipate schizophrenia


Electronic Health Records

Design Motivation
-
One pixel attack
- Why?
(Su et al., 2019)
Design Motivation

-
One pixel attack
- Why?
- Adversarial examples
- Why?
(Goodfellow et al., 2015)
Design Motivation
- Husky vs Wolf task

Design Motivation
- Husky vs Wolf task

Design Motivation
- Husky vs Wolf task

(Ribeiro et al., 2016)
Motivation: NLP
- Explanations in NLP

(Ribeiro et al., 2016)
Motivation: NLP
- Explanations in NLP

(Galassi et al., 2019)
Motivation: NLP
- Explanations in NLP

(Strobelt et al., 2018)
Motivation: NLP
- Explanations in NLP: Rationales
- "a short yet sufficient part of the input text"
(Lei et al., 2016; Bastings et al., 2019)
- "snippets that support the output"
(DeYoung et al., 2020)
- "a short yet sufficient part of the input text"
(Lei et al., 2016)


(DeYoung et al., 2020)
Definitions

Source: xaitutorial2020.github.io
- What is Trustable AI?
- What is explainability? interpretability? transparency?
- To whom we are trying to explain?
- Explain the model or the decision for a particular input?
Definitions
- What is Trustable AI?
- What is explainability? interpretability? transparency?
- To whom we are trying to explain?
- Explain the model or the decision for a particular input?
- Large body of work on analysis and interpretation of NNs!
- See (Doshi-Velez and Kim, 2017; Lipton, 2018; Gilpin et al., 2018; Miller, 2019).
- See AAAI 2020 Explainable AI Tutorial
Definitions
-
Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information
- attention mappings vs gradient probing information
attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions
Works on NLP
-
Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information
- attention mappings vs gradient probing information
-
Is attention interpretable? (Serrano and Smith, 2019)
- attention ablation study, looking for decision shifts
attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions
highest attention weights fail to have a large impact
need to erase a large set of att. weights to flip a decision
Works on NLP
-
Attention is not explanation (Jain and Wallace, 2019)
- attention mappings vs gradient probing information
- attention mappings vs gradient probing information
-
Is attention interpretable? (Serrano and Smith, 2019)
- attention ablation study, looking for decision shifts
Works on NLP
attention is uncorrelated with gradient-based measures
different attention weights yield equivalent predictions
highest attention weights fail to have a large impact
need to erase a large set of att. weights to flip a decision
- As a importance measure, it fails to explain model decisions
-
Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests
- questions the conclusions of the previous and proposes various explainability tests
Works on NLP
-
Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests
- questions the conclusions of the previous and proposes various explainability tests
-
How should we define and evaluate faithfulness? (Jacovi and Goldberg, 2020)
- Plausibility: how convincing the interpretation is to humans
- Faithfulness: how accurately it reflects the true reasoning process of the model
Works on NLP
-
Attention is not not explanation (Wiegreffe and Pinter, 2019)
- questions the conclusions of the previous and proposes various explainability tests
- questions the conclusions of the previous and proposes various explainability tests
-
How should we define and evaluate faithfulness? (Jacovi and Goldberg, 2020)
- Plausibility: how convincing the interpretation is to humans
-
Faithfulness: how accurately it reflects the true reasoning process of the model
- Graded notion of faithfulness
Works on NLP
- Rationalizer models
- Arguably more faithful
- Arguably more faithful
- Classifier \(f_\theta\) that, given latent
masks \(z\) and \(x\) as input, output \(y\)
Works on NLP

(Bastings et al., 2019)
- Rationale extractor \(g_\phi\) that generates masks \(z\)
(Bastings et al., 2019)
(Lei et al., 2016)
- Rationalizer models
- Arguably more faithful
- Arguably more faithful
- Stochastic gradients
- Reinforce
- Reparameterization trick
- Encourage sparsity and contiguity directly in the loss fn
Works on NLP
sparse
rationales
contiguous rationales

(Bastings et al., 2019)
class. loss
-
Comprehensive vs sufficient rationales (DeYoung et al., 2020)
- Com. have all necessary information to make a decision
- Suf. have enough information to make a decision
Works on NLP


Forest
Forest
Forest
- Classical feature selection
- Happens statically at run time
- After training, irrelevant features
are permanently deleted from the model
Revisiting Feature Selection
- Classical feature selection
- Happens statically at run time
- After training, irrelevant features
are permanently deleted from the model
- Prediction explainability
- Happens dynamically at run time
- A feature not relevant for a particular
input can be relevant for another
Revisiting Feature Selection
- Typology (Guyon and Elisseeff, 2003)
Revisiting Feature Selection



Wrappers: “utilize the learning machine of interest as a black box to score subsets of variable according to their predictive power” (e.g. forward selection)
Filters: decide to include/exclude a feature based on an importance metric (e.g. pairwise mutual information)
Embedded: embed feature selection within the learning algorithm by using a sparse regularizer
(e.g. ℓ1-norm)
- Static: feature selector & learning algorithm
- Dynamic: explainer & classifier
Revisiting Feature Selection
| static | dynamic | |
|---|---|---|
| wrapper | Forward selection Backward elimination |
Representation erasure Leave one out LIME |
- Static: feature selector & learning algorithm
- Dynamic: explainer & classifier
Revisiting Feature Selection
| static | dynamic | |
|---|---|---|
| wrapper | Forward selection Backward elimination |
Representation erasure Leave one out LIME |
| filter | Pointwise mutual information Recursive feature elimination |
Input gradient Top-k attention |
- Static: feature selector & learning algorithm
- Dynamic: explainer & classifier
Revisiting Feature Selection
| static | dynamic | |
|---|---|---|
| wrapper | Forward selection Backward elimination |
Representation erasure Leave one out LIME |
| filter | Pointwise mutual information Recursive feature elimination |
Input gradient Top-k attention |
| embedded | ℓ1-regularization elastic net |
Stochastic attention Sparse attention |
Attention
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$
Attention
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

(Niculae , 2018)
$$ \exp(\mathbf{s}_j) / \sum_k \exp(\mathbf{s}_k) $$
softmax:
Attention
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$
$$ \exp(\mathbf{s}_j) / \sum_k \exp(\mathbf{s}_k) $$
Dense
Less faithful
Not an embedded method!
softmax:
Attention
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$
$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \mathbf{s}||_2^2 $$
sparsemax:

(Niculae , 2018)
Attention
query keys values
$$\mathbf{q} \in \mathbb{R}^{ d_q}$$
$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$
$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$
1. Compute a score between q and each kj
$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$
2. Map scores to probabilities
$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$
$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \mathbf{s}||_2^2 $$
sparsemax:
Sparse
More faithful
An embedded method!
Sparse Attention
- More generally
- α-entmax transformation (Peters et al., 2019):
Tsallis α-entropy regularizer

(Peters et al. , 2019)
Explainability as Communication
- Ability of an explainer to communicate the rationale of a decision in terms that can be understood by a human
- + success of communication + plausability
- Human-grounded evaluation through forward simulation/prediction (Doshi-Velez and Kim, 2017, §3.2)

Communication Framework
- Classifier \(C\)
- \(\hat{y} = C(x) \approx y\)
- hidden representations \(h\)
- Explainer \(E\)
- \(m = E(x, \hat{y}, h)\)
- \(m \in \mathcal{M}\) is regarded as a “rationale” for \(\hat{y}\)
- Layperson \(L\)
- \(\tilde{y} = L(m)\)
- simple model (e.g., a linear classifier)

Communication Framework
Classifier
Explainer
Layperson
\(\hat{y} = C(x)\)
\(m = E(x, \hat{y}, h) \in \mathcal{M} \)
\(\tilde{y} = L(m)\)
- The communication is successful if \(\hat{y} = \tilde{y}\)
Communication Framework
Classifier
Explainer
Layperson
\(\hat{y} = C(x)\)
\(m = E(x, \hat{y}, h) \in \mathcal{M} \)
\(\tilde{y} = L(m)\)
- The communication is successful if \(\hat{y} = \tilde{y}\)
- Communication Success Rate (CSR)
- A quantifiable measure of explainability
\(\uparrow\) CSR \(\implies\) informative messages
Communication Framework
- Relation to filters and wrappers:
- \(C\) and \(E\) are separate components
- \(E\) works as a post-hoc explainer
- Relation to embedded methods:
- \(E\) is embedded as an internal component of \(C\)
- e.g. rationalizer models and sparse attention
Classifier
Explainer
Layperson
\(\hat{y} = C(x)\)
\(m = E(x, \hat{y}, h) \in \mathcal{M} \)
\(\tilde{y} = L(m)\)
Communication Framework
- Relation to filters and wrappers:
- \(C\) and \(E\) are separate components
- \(E\) works as a post-hoc explainer
- Relation to embedded methods:
- \(E\) is embedded as an internal component of \(C\)
- e.g. rationalizer models and sparse attention
Possible messages?
Possible explainers?
Classifier
Explainer
Layperson
\(\hat{y} = C(x)\)
\(m = E(x, \hat{y}, h) \in \mathcal{M} \)
\(\tilde{y} = L(m)\)
Comm. Framework: Messages
- Rationales
- BoW
- Word embeddings

Comm. Framework: Messages
- Rationales
- BoW
- Word embeddings
- Prototypes
- Criticisms
- ...
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
- Erasure
- Filters
- Gradient-based
- Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
- Erasure
- Filters
- Gradient-based
- Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
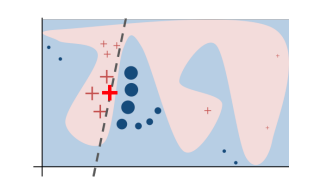
- Perturbation method
- Areas = complex decision boundaries
- Bold red cross = instance we want to explain
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
- Erasure
- Filters
- Gradient-based
- Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
why this movie is so bad ?
90%
80%
why movie is so bad ?
89%
why this movie is so ?
58%
this movie is so bad ?
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
-
Erasure
- Filters
- Gradient-based
- Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
why this movie is so bad ?
measure
(grad/attn)
why this movie is so bad ?
why this movie is so ?
why this movie is so ?
this movie is so ?
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
- Erasure
- Filters
- Gradient-based
-
Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
why this movie is so bad ?
measure
(grad/attn)
why this movie is so bad ?
why bad ?top k
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
- Erasure
- Filters
- Gradient-based
- Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
why this movie is so bad ?
measure
(grad/attn)
why movie bad ?
why this movie is so bad ?
Comm. Framework: Explainers
- Wrappers
- LIME
- Leave one out
-
Erasure
- Filters
- Gradient-based
-
Top-k attention
- Embedded
- Stochastic attention
- Sparse attention
Humans
Comm. Framework: Explainers
- So far
- \(E\) queries \(C\) multiple times
- Or \(E\) is embedded in \(C\) and we access \(m\)
- But
- \(E\) can be seen as a separate trainable model!

Comm. Framework: Explainers
- So far
- \(E\) queries \(C\) multiple times
- Or \(E\) is embedded in \(C\) and we access \(m\)
- But
- \(E\) can be seen as a separate trainable model!

Comm. Framework: Explainers
- Joint training of \(E\) and \(L\)
- Cooperative game
- Maximize CSR
- Let \(E_\theta\) and \(L_\phi\), and input \((x, \hat{y})\)
- Multitask objective
- Reconstruction term: \(\mathcal{L}(\phi, \theta) = -\log p_\phi(\hat{y} \mid m)\)
- Faithfulness term: \(\Omega(\theta) = \|\tilde{h}(E_{\theta}), h\|^2\)
\(\mathcal{L}_{\Omega}(\phi, \theta) := \mathcal{L}(\phi, \theta) + \lambda \Omega(\theta)\)
C's hidden reps.
E's predictions of h reps.
C's predictions are passed as input to E
message
Comm. Framework: Explainers
- Joint training of \(E\) and \(L\)
- Cooperative game
- Maximize CSR
- Let \(E_\theta\) and \(L_\phi\), and input \((x, \hat{y})\)
- Multitask objective
- Reconstruction term: \(\mathcal{L}(\phi, \theta) = -\log p_\phi(\hat{y} \mid m)\)
- Faithfulness term: \(\Omega(\theta) = \|\tilde{h}(E_{\theta}), h\|^2\)
\(\mathcal{L}_{\Omega}(\phi, \theta) := \mathcal{L}(\phi, \theta) + \lambda \Omega(\theta)\)
C's hidden reps.
E's predictions of h reps.
C's predictions are passed as input to E
message
Comm. Framework: Explainers
- Trivial protocol
why this movie is so bad ?
\(L\)
I think this is a good film
\(L\)
- Heuristics to avoid it
- Forbid stop words from being selected by \(E\)
- \(E\) will access \(\hat{y}\) with a chance of \(\beta\) (e.g. \(\beta=20\%\))
iter
\(\beta\)
20%
End of training
Experiments

Experiments

Experiments
- Classifier \(C\)
- Embedding
- BiLSTM
- Additive attention with \(\alpha \in \{1.0, \, 1.5, \, 2.0\}\)
- Linear output
- Explainer \(E\)
- \(m\) = BoWs
- \(m\) = BoWs
- Layperson \(L\)
- Linear
softmax
1.5-entmax
sparsemax
Experiments
IMDB
BoW
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
92%
90%
88%
86%
SNLI
BoW
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
84%
80%
76%
72%
68%
- Classifier results (accuracy)
Experiments
- Communication results (CSR)
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
Top-k Gradient
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
83% 81% 79% 77% 75%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Experiments
- Communication results (CSR)
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
Top-k Gradient
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
83% 81% 79% 77% 75%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Experiments
- Communication results (CSR)
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
Top-k Gradient
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
83% 81% 79% 77% 75%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Experiments
- Communication results (accuracy of \(L\))
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
75%
73%
71%
69%
67%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Top-k Gradient
Experiments
- Communication results (accuracy of \(L\))
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
75%
73%
71%
69%
67%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Top-k Gradient
Experiments
- Communication results (accuracy of \(L\))
IMDB
Random
Erasure
Top-k
ent
Top-k soft
95% 93% 91% 89% 87% 85%
68%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
Random
Erasure
Top-k
ent
Top-k soft
75%
73%
71%
69%
67%
Top-k
sparse
Select.
ent
Select.
sparse
Bernoulli
HardKuma
\(C_{soft}\)
\(C_{sparse}\)
\(C_{ent}\)
\(C_{bern}\)
\(C_{hk}\)
\(C_{soft}\)
\(C_{soft}\)
\(C_{ent}\)
\(C_{sparse}\)
\(C_{soft}\)
SNLI
Top-k Gradient
Top-k Gradient
Experiments
- Impact of the sparsity (length of the message)

IMDB
SNLI

emb. 1.5-entmax
emb. sparsemax
text length
emb. sparsemax
emb. 1.5-entmax
text length
Experiments
- Impact of the sparsity (length of the message)
CSR does not increase monotonically with k

IMDB
SNLI

Experiments
- Impact of the sparsity (length of the message)
IWSLT

\(k\)
Human Evaluation
- Joint \(E\) and \(L\) model
- Maximize the communication
- Maximize the communication
- Human \(L\)
- 200 random examples
- Explanations shuffled
- Human \(E\)
- e-SNLI corpus
- Human highlights
(nonneutral pairs only) - CSR = ACC always


Human Evaluation

Human Evaluation

Human Evaluation

Human Evaluation

Human Evaluation


Human Evaluation


Final Remarks
- A unified framework that regards explainability as a communication problem
- Flexibility between \(C\), \(E\) and \(L\)
- A link between classical feature selection and expl. methods
- Embedded method based on selective sparse attention
- Post-hoc explainer that is trained to optimize CSR
Final Remarks
- A unified framework that regards explainability as a communication problem
- Flexibility between \(C\), \(E\) and \(L\)
- A link between classical feature selection and expl. methods
- Embedded method based on selective sparse attention
-
Post-hoc explainer that is trained to optimize CSR
- Attention and erasure get higher CSR than gradient
- Embedded selective attention is effective while being simpler to train than rationalizers
Refs
- Benjamin Wilson, Judy Hoffman, and Jamie Morgenstern. Predictive inequity in object detection. arXiv preprint arXiv:1902.11097, 2019
- Riccardo Miotto, Li Li, Brian A Kidd, and Joel T Dudley. Deep patient: an unsupervised representation to predict the future of patients from the electronic health records.Scientific reports, 6:26094, 2016
- Su, Jiawei, Danilo Vasconcellos Vargas, and Kouichi Sakurai. "One pixel attack for fooling deep neural networks." IEEE Transactions on Evolutionary Computation 23.5 (2019): 828-841
- Goodfellow, Ian J., Jonathon Shlens, and Christian Szegedy. "Explaining and harnessing adversarial examples." arXiv preprint arXiv:1412.6572 (2014)
- Marco Tulio Ribeiro, Sameer Singh, and Carlos Guestrin. Why should i trust you? Explaining the predictions of any classifier. In Proceedings of the 22nd ACMSIGKDD international conference on knowledge discovery and data mining, pages 1135–1144. ACM, 2016
Refs
- Strobelt, Hendrik, et al. "Seq 2seq-vis: A visual debugging tool for sequence-to-sequence models." IEEE transactions on visualization and computer graphics 25.1 (2018): 353-363.
- Galassi, Andrea, Marco Lippi, and Paolo Torroni. "Attention in Natural Language Processing." 2019. Arxiv 1902.02181
- Niculae, Vlad. "Learning Deep Models with Linguistically-Inspired Structure." (2018).
- Ben Peters, Vlad Niculae, and Andre FT Martins. 2019. Sparse sequence-to-sequence models. Proc. ACL.
- Goncalo M Correia, Vlad Niculae, and Andre FT Martins. 2019. Adaptively sparse transformers. In Proc. EMNLP-IJCNLP, pages 2174–2184.
- Joost Bastings, Wilker Aziz, and Ivan Titov. 2019. Interpretable neural predictions with differentiable binary variables. In Proc. ACL.
Refs
- Jay DeYoung, Sarthak Jain, Nazneen Fatema Rajani, Eric Lehman, Caiming Xiong, Richard Socher, and Byron C Wallace. 2020. Eraser: A benchmark to evaluate rationalized nlp models. arXiv preprint arXiv:1911.03429.
- Leilani H Gilpin, David Bau, Ben Z Yuan, Ayesha Bajwa, Michael Specter, and Lalana Kagal. 2018. Explaining explanations: An overview of interpretability of machine learning. In Proc. DSAA, pages 80–89.
- Alon Jacovi and Yoav Goldberg. 2020. Towards faithfully interpretable nlp systems: How should we define and evaluate faithfulness? In Proc. of ACL.
- Sarthak Jain and Byron C Wallace. 2019. Attention is not explanation. In Proc. NAACL-HLT.
- Tao Lei, Regina Barzilay, and Tommi Jaakkola. 2016. Rationalizing neural predictions. In Proc. EMNLP, pages 107–117.
- Zachary C. Lipton. 2018. The mythos of model interpretability. Commun. ACM, 61(10):36–43.
Refs
- Tim Miller. 2019. Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence, 267:1–38.
- Cynthia Rudin. 2019. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 1(5):206–215.
- Sofia Serrano and Noah A Smith. 2019. Is attention interpretable? In Proc. ACL.
- Sarah Wiegreffe and Yuval Pinter. 2019. Attention is not not explanation. In Proc. EMNLP-IJCNLP.
- Mo Yu, Shiyu Chang, Yang Zhang, and Tommi Jaakkola. 2019. Rethinking cooperative rationalization: Introspective extraction and complement control. InProc. EMNLP-IJCNLP, pages 4085–4094.
Thank you for your attention!
marcos.treviso@tecnico.ulisboa.pt
Social Motivation: Critical Systems

Motivation: NLP
- Explanations in NLP: Rationales


(DeYoung et al., 2020)

Definitions
Source: xaitutorial2020.github.io

- What is Trustable AI?
- What is explainability? interpretability? transparency?
- To whom we are trying to explain?
- Explain the model or the decision for a particular input?
- Large body of work on analysis and interpretation of NNs!
- See (Doshi-Velez and Kim, 2017; Lipton, 2018; Gilpin et al., 2018; Miller, 2019).
- See AAAI 2020 Explainable AI Tutorial
Definitions
It's easier to poke holes in a study than to run one yourself.
COVID-19 Data Dives: The Takeaways From Seroprevalence Surveys.
Natalie E. Dean. May/2020. Medscape
Human Evaluation

