Transformers

Marcos V. Treviso

Instituto de Telecomunicações

December 19, 2019

Refs

Attention is all you need
https://arxiv.org/abs/1706.03762

 

The illustrated transformer
http://jalammar.github.io/illustrated-transformer/

 

The annotated transformer
http://nlp.seas.harvard.edu/2018/04/03/attention.html
 

Łukasz Kaiser’s presentation
https://www.youtube.com/watch?v=rBCqOTEfxvg

A high-level look

Encoder-Decoder

context vector

Encoder

Decoder

↺

↺

BiLSTM

LSTM

$$x_1 \, x_2 \,...\, x_n$$

$$y_1 \, y_2 \,...\, y_m$$

Encoder-Decoder

Encoder

Decoder

BiLSTM

LSTM

$$x_1 \, x_2 \,...\, x_n$$

context vector

$$y_1 \, y_2 \,...\, y_m$$

↺

↺

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1.  Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1.  Compute a score between q and each kj

           dot-product:

    bilinear:

 additive:

neural net:

$$\mathbf{k}_j^\top \mathbf{q}, \quad (d_q == d_k)$$

$$\mathbf{k}_j^\top \mathbf{W} \mathbf{q}, \quad \mathbf{W} \in \mathbb{R}^{d_k \times d_q}$$

$$\mathbf{v}^\top \mathrm{tanh}(\mathbf{W}_1 \mathbf{k}_j + \mathbf{W}_2 \mathbf{q})$$

$$\mathrm{MLP}(\mathbf{q}, \mathbf{k}_j); \quad \mathrm{CNN}(\mathbf{q}, \mathbf{K}); \quad ...$$

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1.  Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2.  Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1.  Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2.  Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

           softmax:

 

sparsemax:

$$ \exp(\mathbf{s}_j) / \sum_k \exp(\mathbf{s}_k) $$

$$ \mathrm{argmin}_{\mathbf{p} \in \triangle^n} \,||\mathbf{p} - \mathbf{s}||_2^2 $$

Attention

query                keys                 values

$$\mathbf{q} \in \mathbb{R}^{ d_q}$$

$$\mathbf{K} \in \mathbb{R}^{n \times d_k}$$

$$\mathbf{V} \in \mathbb{R}^{n \times d_v}$$

1.  Compute a score between q and each kj

$$\mathbf{s} = \mathrm{score}(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{n} $$

2.  Map scores to probabilities

$$\mathbf{p} = \pi(\mathbf{s}) \in \triangle^{n} $$

3.  Combine values via a weighted sum

$$\mathbf{z} = \sum\limits_{i=1}^{m} \mathbf{p}_i \mathbf{V}_i \in \mathbb{R}^{d_v}$$

Drawbacks of RNNs

  • Sequential mechanism prohibits parallelization

 

 

 

 

 

  • Long-range dependencies are tricky, despite gating

$$x_1$$

$$x_2$$

...

$$x_n$$

$$x_1 \quad x_2 \quad x_3 \quad x_4 \quad x_5 \quad x_6 \quad x_7 \quad x_8 \quad x_9 \quad ... \quad x_{n-1} \quad x_{n}$$

Transformer

Transformer

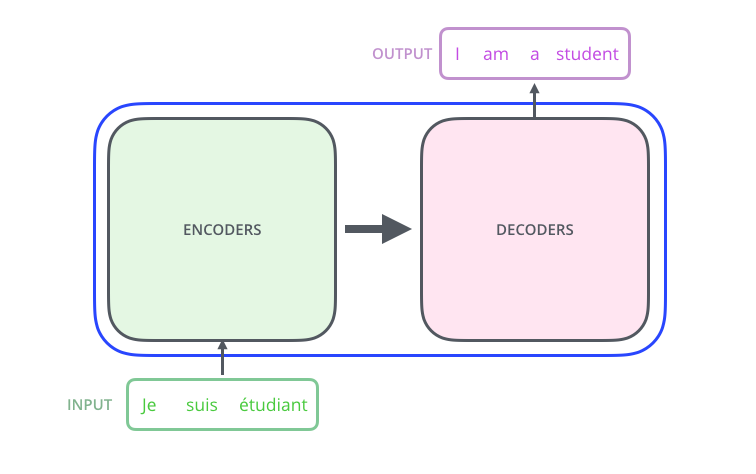
$$x_1 \, x_2 \,...\, x_n$$

$$\mathbf{r}_1 \, \mathbf{r}_2 \,...\, \mathbf{r}_n$$

$$y_1 \, y_2 \,...\, y_m$$

encode

decode

Transformer

Transformer

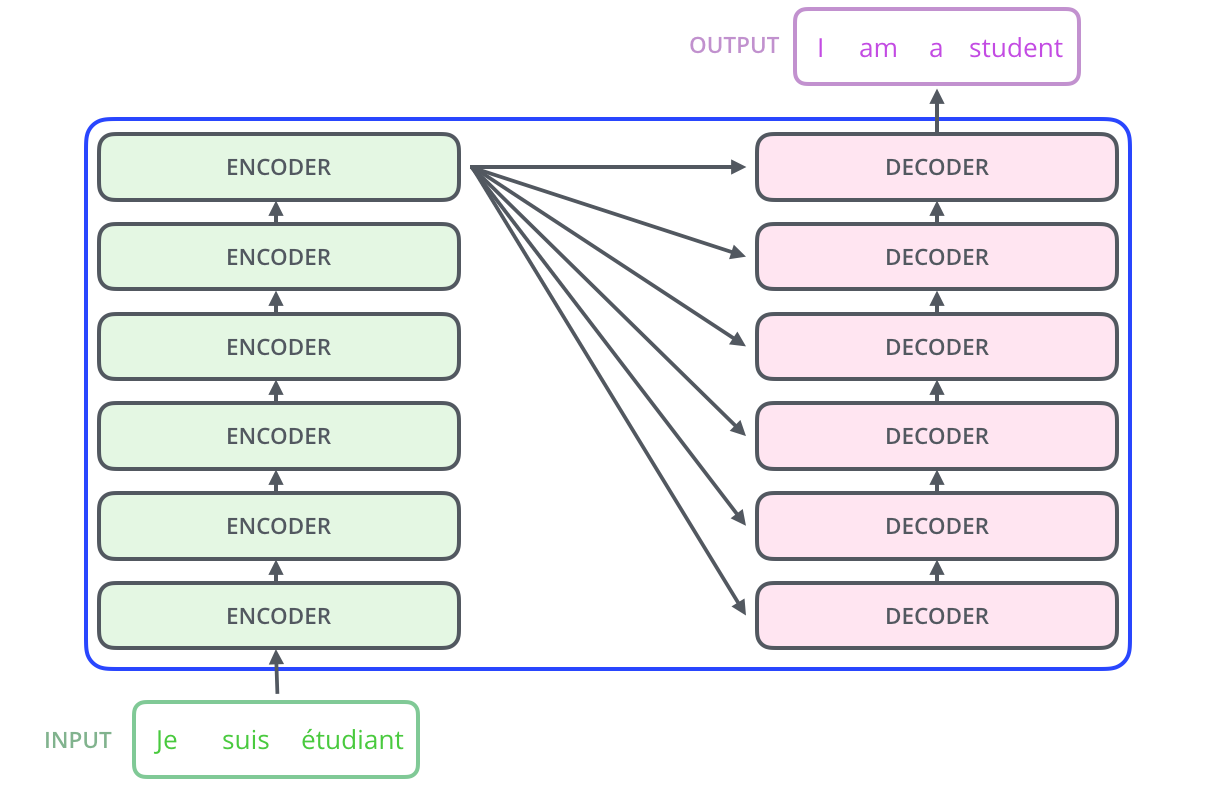
Transformer blocks

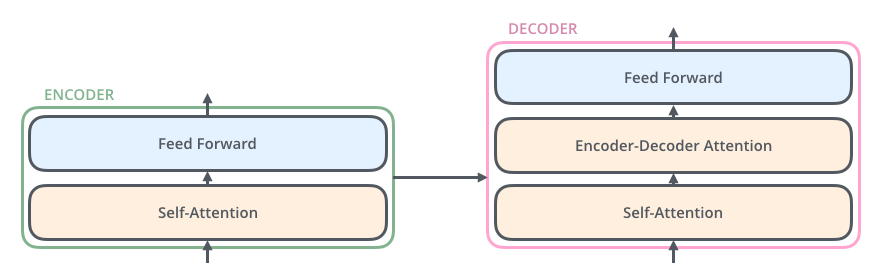
The encoder

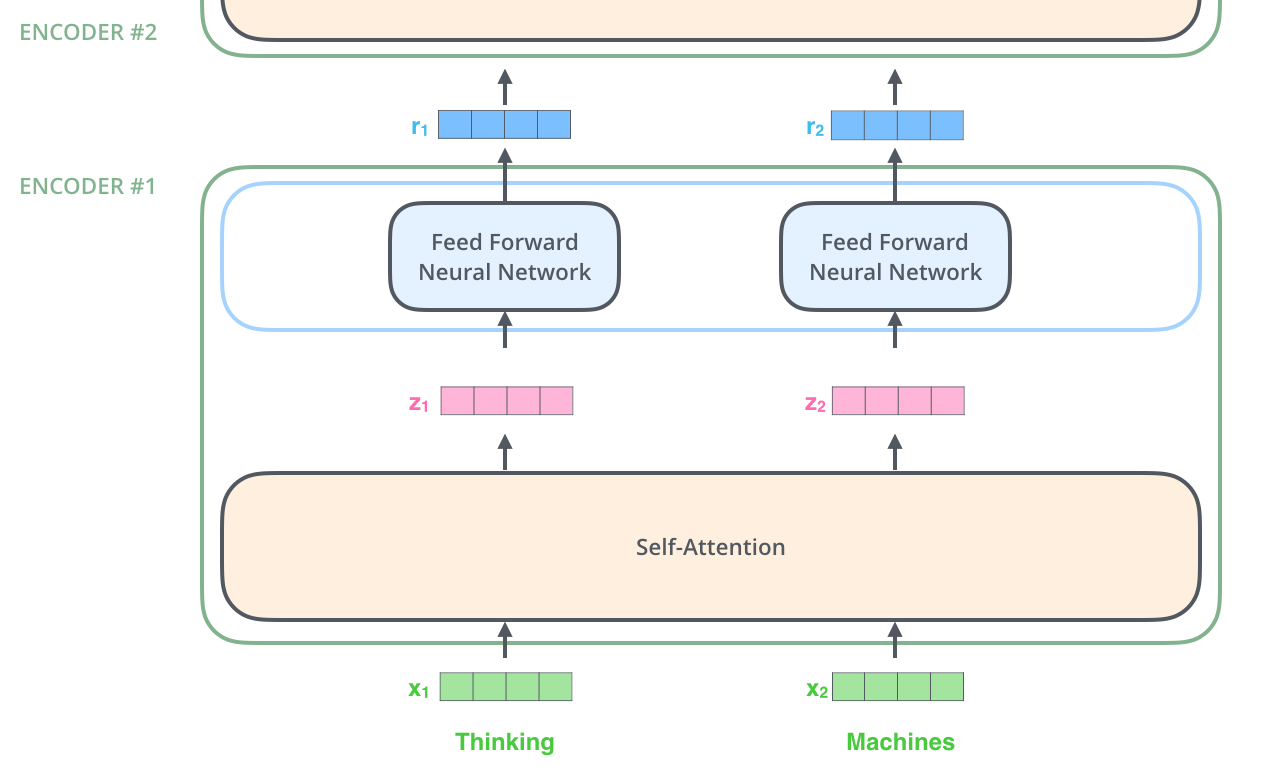
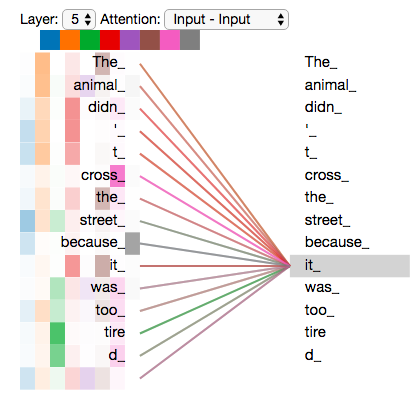
Self-attention

"The animal didn't cross the street because it was too tired"

Self-attention

"The animal didn't cross the street because it was too tired"

$$\mathbf{Q}_j = \mathbf{K}_j = \mathbf{V}_j \in \mathbb{R}^{d} \quad \iff$$

dot-product scorer!

Transformer self-attention

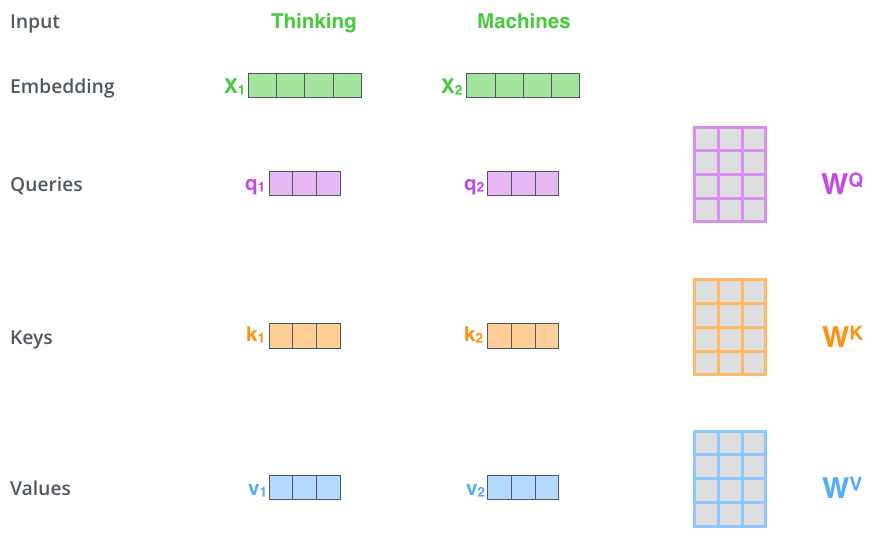
Transformer self-attention

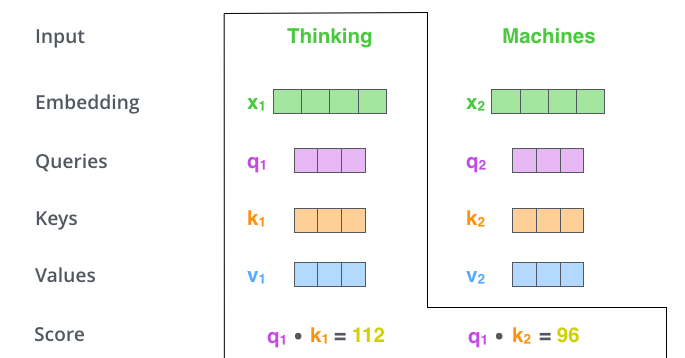
Transformer self-attention

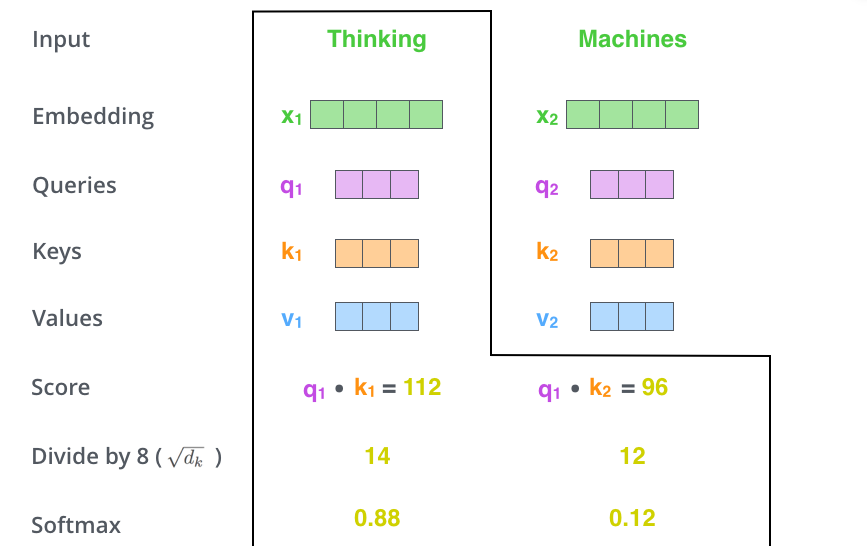
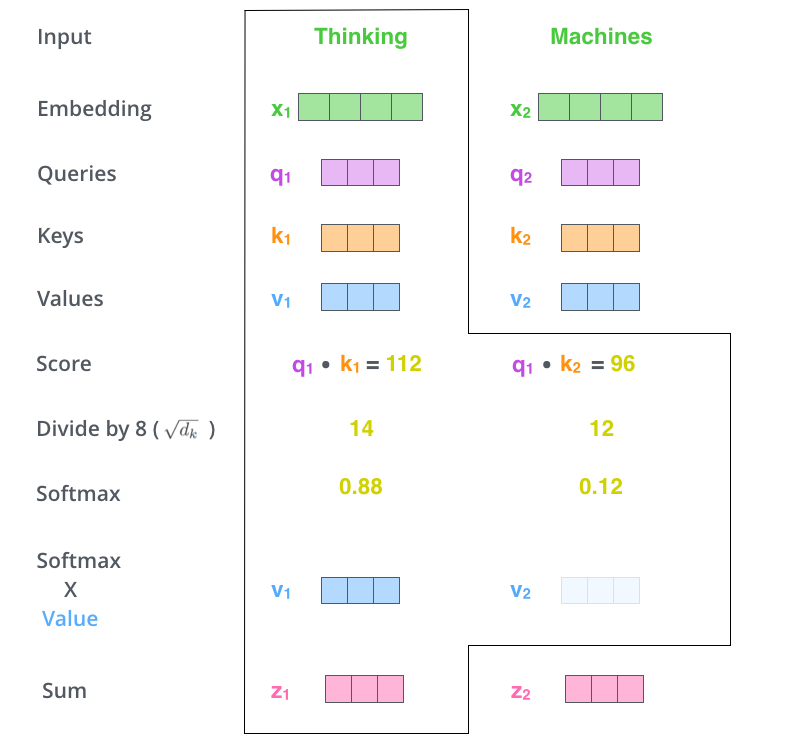
Matrix calculation

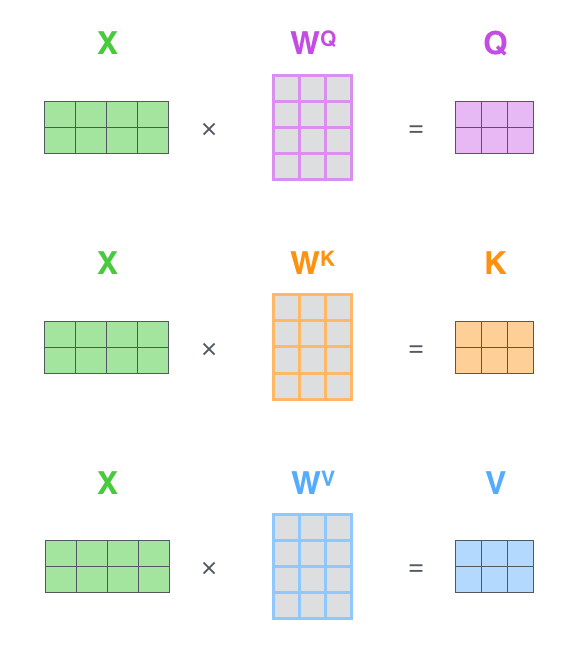
Matrix calculation

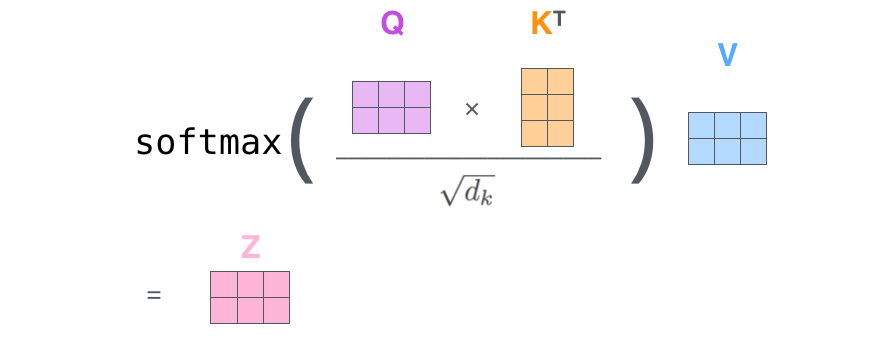
Matrix calculation

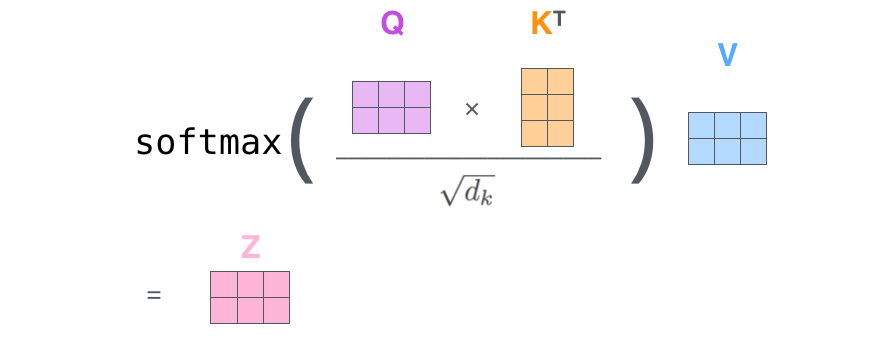
$$\mathbf{S} = \mathrm{score}(\mathbf{Q}, \mathbf{K}) \in \mathbb{R}^{n \times n} $$

$$\mathbf{P} = \pi(\mathbf{S}) \in \triangle^{n \times n} $$

$$\mathbf{Z} = \mathbf{P} \mathbf{V} \in \mathbb{R}^{n \times d}$$

$$\mathbf{Z} = \mathrm{softmax}\Big(\frac{\mathbf{Q} \mathbf{K}^\top}{\sqrt{d_k}}\Big) \mathbf{V} $$

\Bigg\{

$$\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{n \times d}$$

Problem of self-attention

  • Convolution: a different linear transformation for each relative position
           > Allows you to distinguish what information came from where

 

  • Self-attention: a weighted average :(

Fix: multi-head attention

  • Multiple attention layers (heads) in parallel
  • Each head uses different linear transformations
  • Attention layer with multiple “representation subspaces”

Multi-head attention

2 heads

all heads (8)

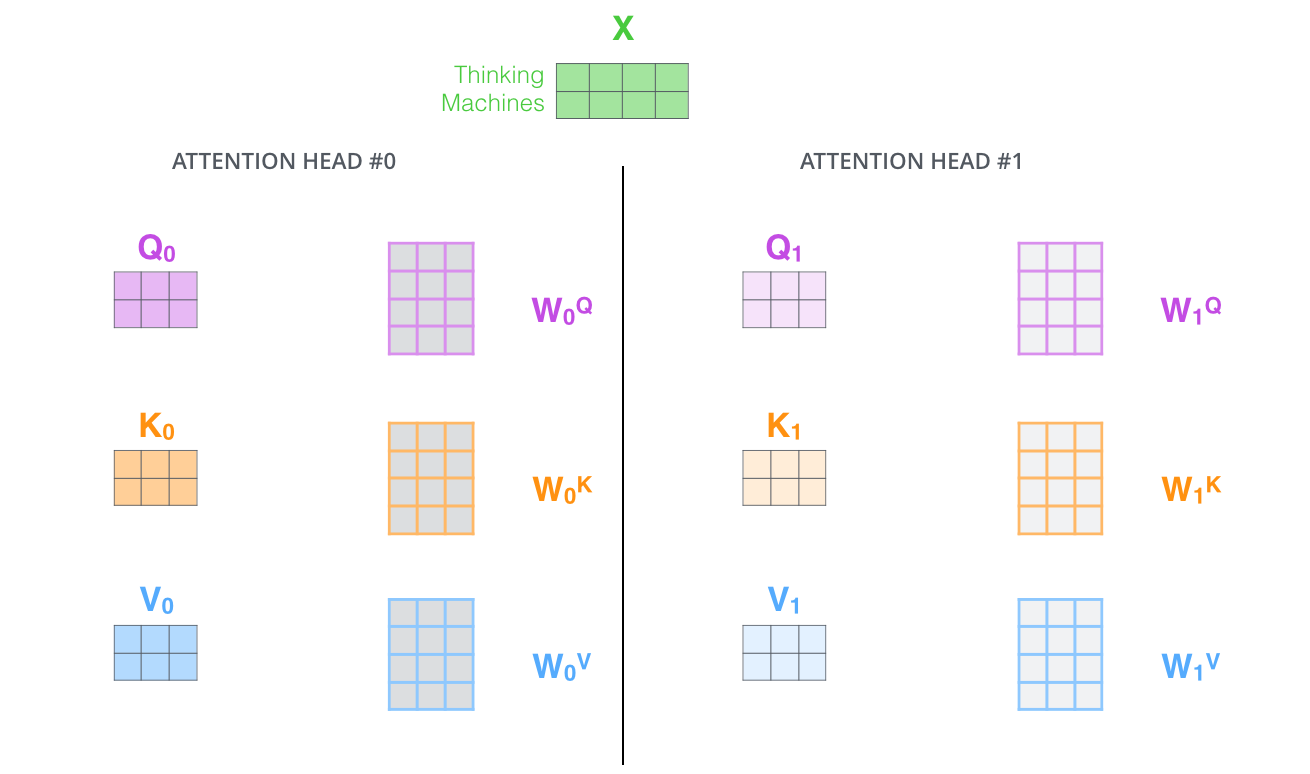
Multi-head attention

Multi-head attention

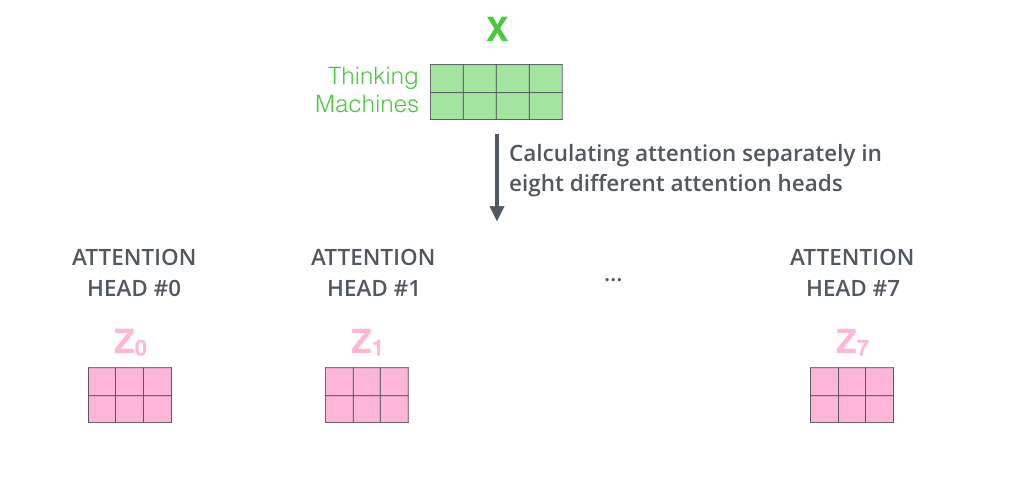
Multi-head attention

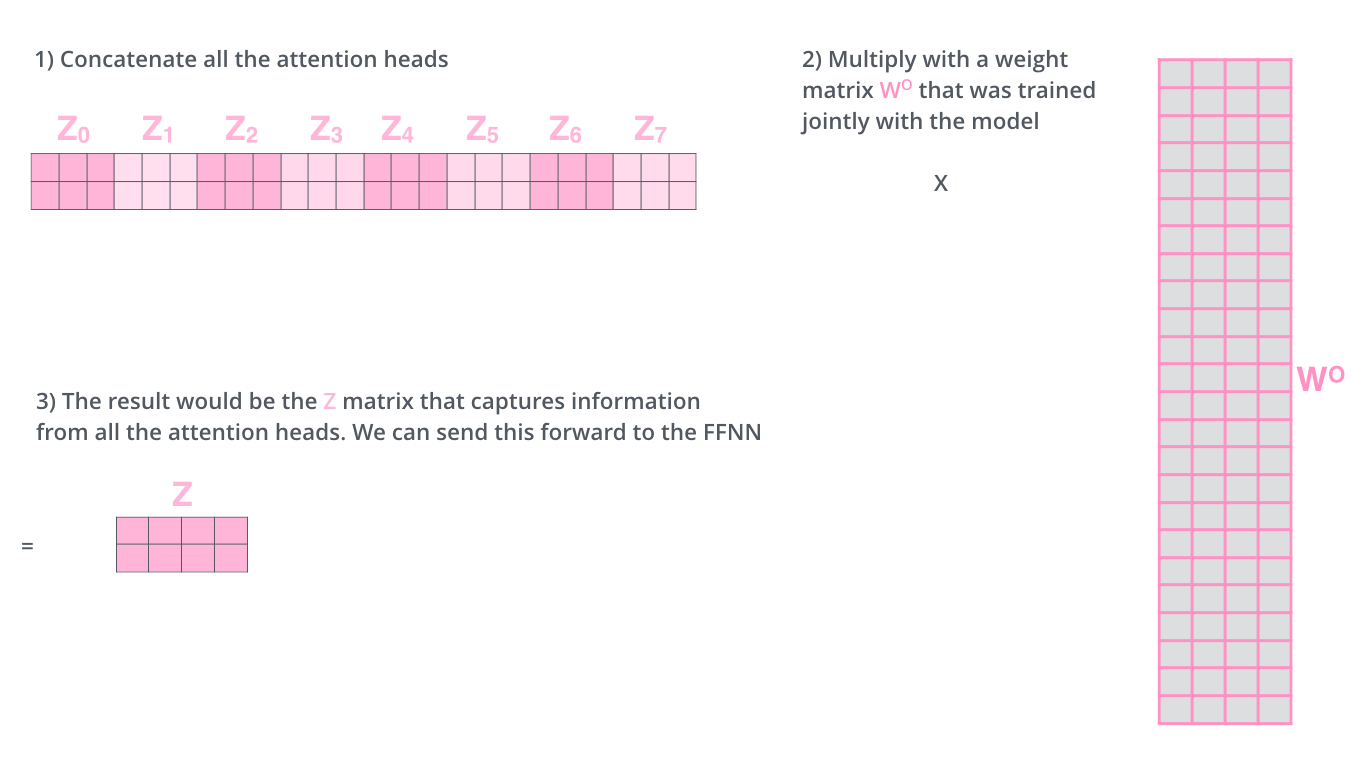
Multi-head attention

\mathrm{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \mathrm{Concat}(\mathbf{Z}_1, \mathbf{Z}_2, ..., \mathbf{Z}_h)\mathbf{W}^O
\mathbf{Z}_i = \mathrm{Attention}(\mathbf{Q}\mathbf{W}^Q_i, \mathbf{K}\mathbf{W}^K_i, \mathbf{V}\mathbf{W}^V_i)
\Big\{

Multi-head attention

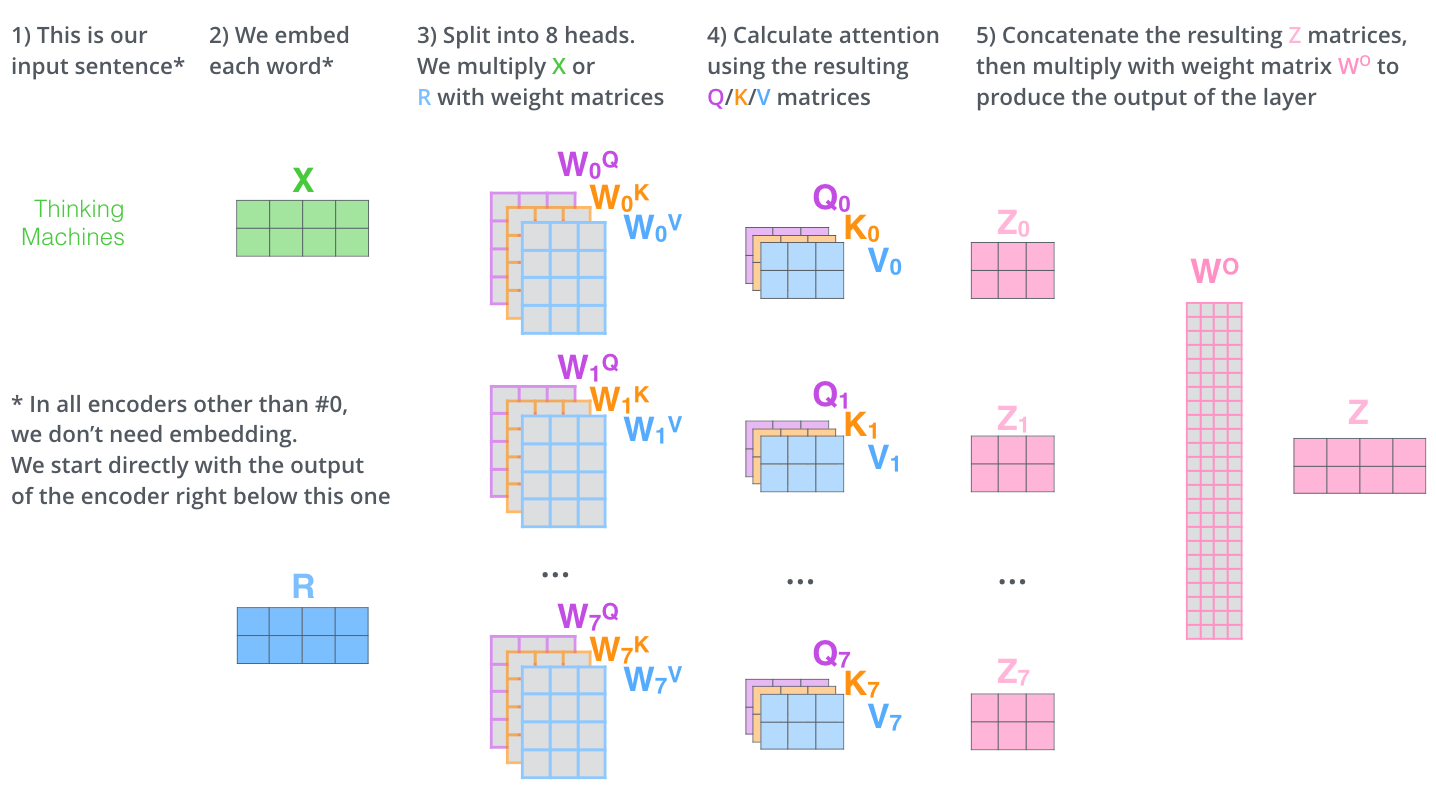
Positional encoding

  • A way to account for the order of the words in the seq.

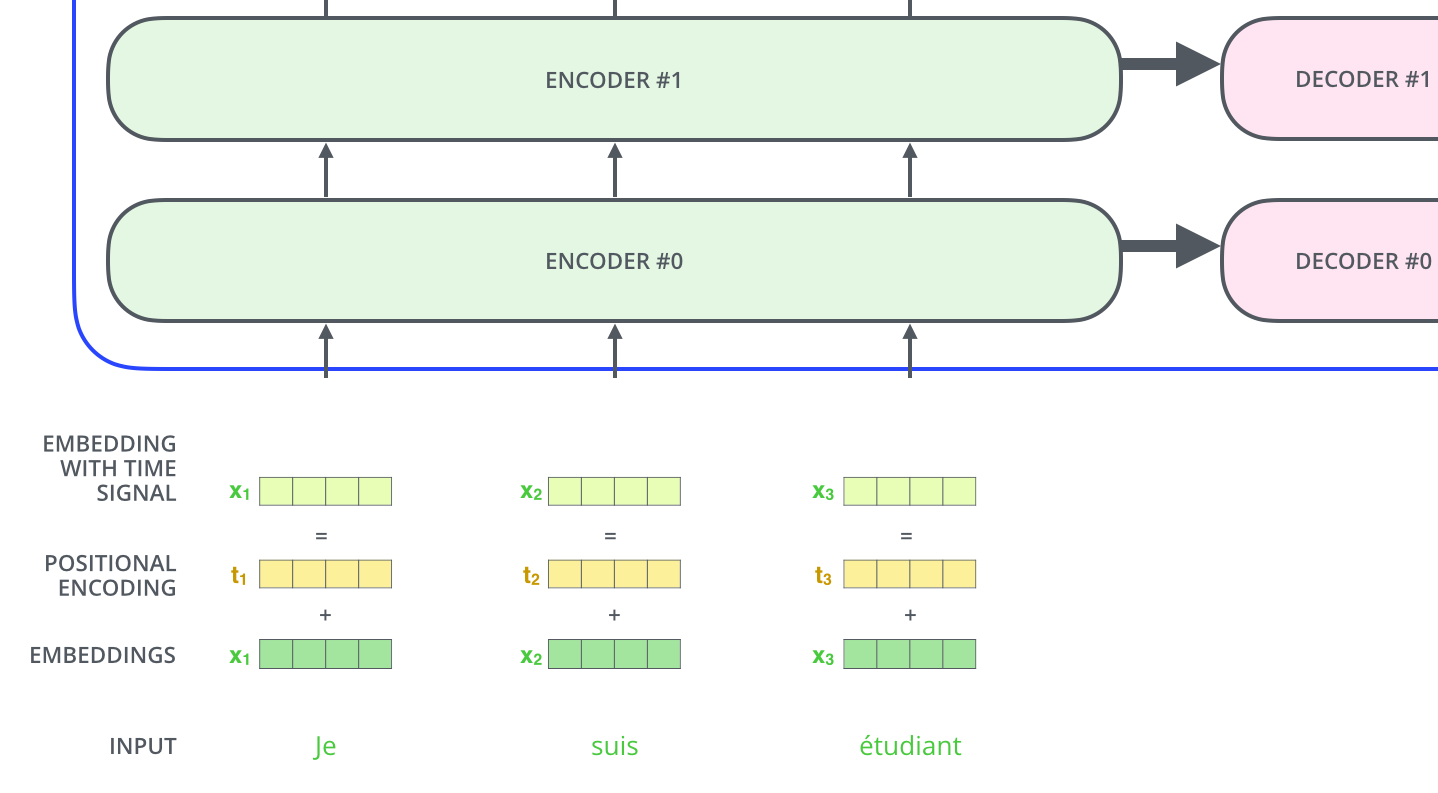
Positional encoding

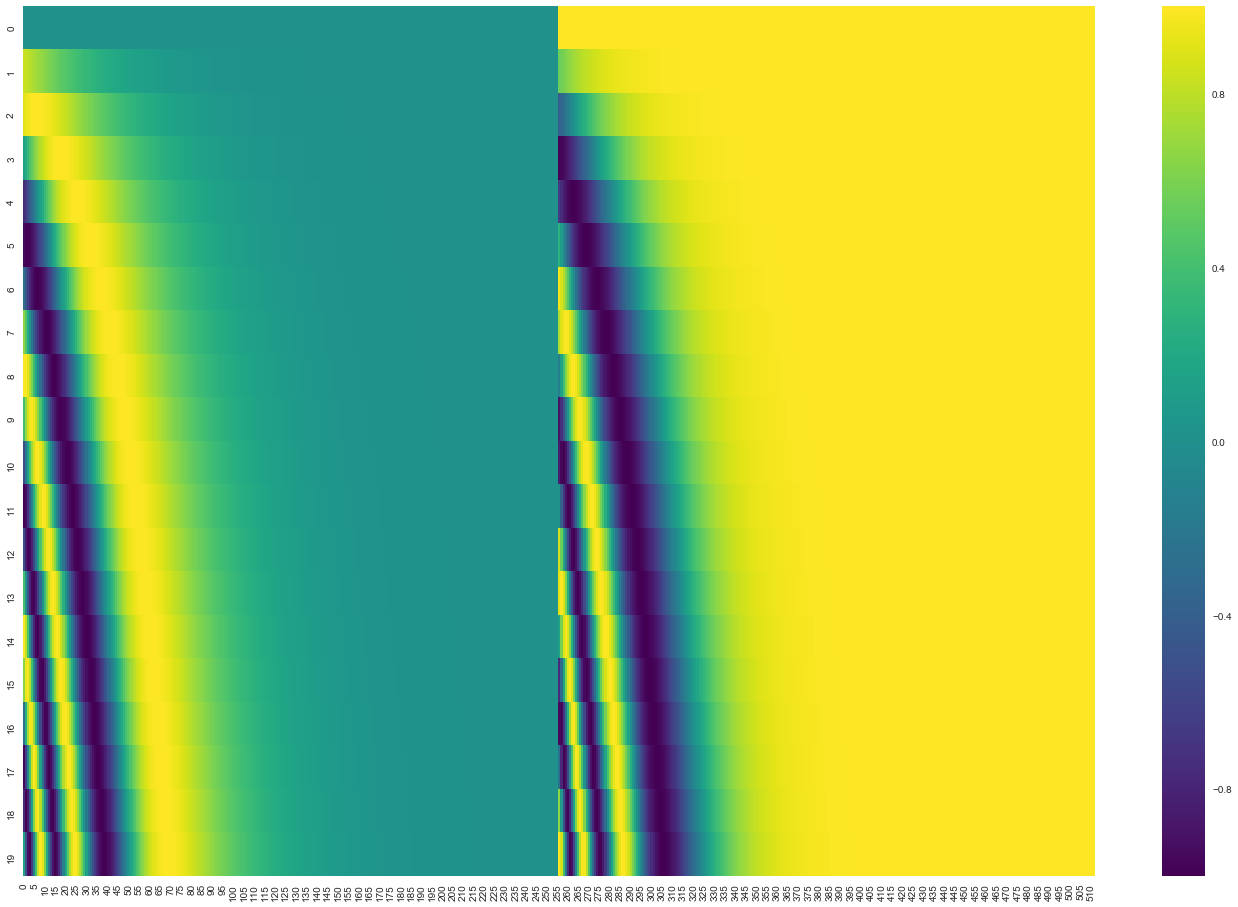
PE_{(pos, 2i)} = \sin\Big(\frac{pos}{10000^{2i/d}}\Big) \qquad PE_{(pos, 2i+1)} = \cos\Big(\frac{pos}{10000^{2i/d}}\Big)

Positional encoding

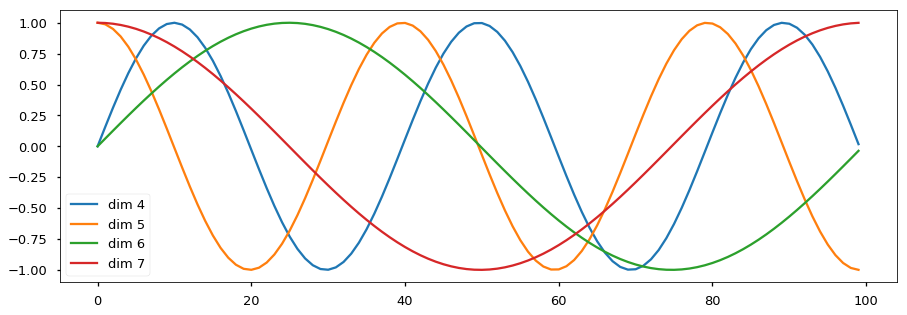
PE_{(pos, 2i)} = \sin\Big(\frac{pos}{10000^{2i/d}}\Big) \qquad PE_{(pos, 2i+1)} = \cos\Big(\frac{pos}{10000^{2i/d}}\Big)

Residuals & LayerNorm

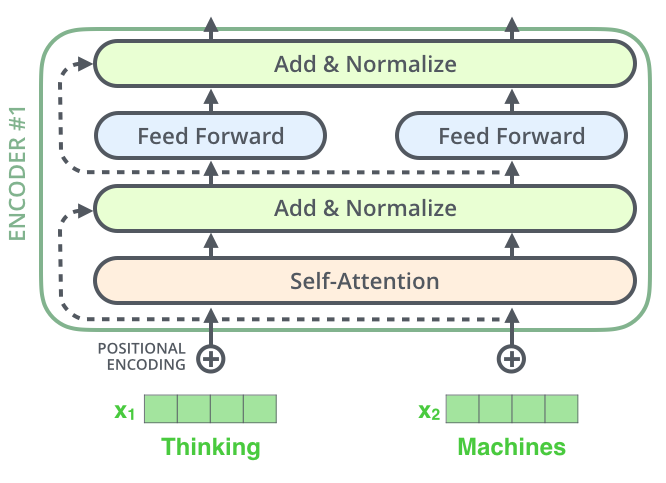
Residuals & LayerNorm

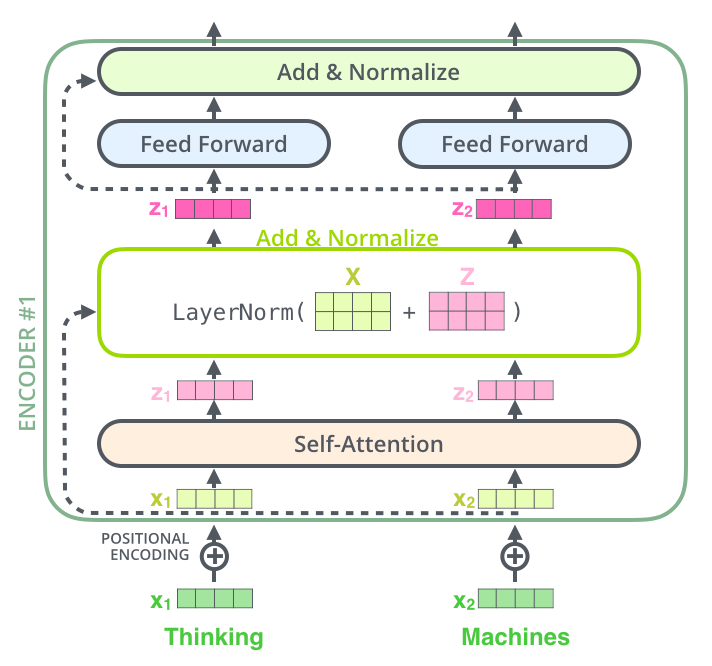
Residuals & LayerNorm

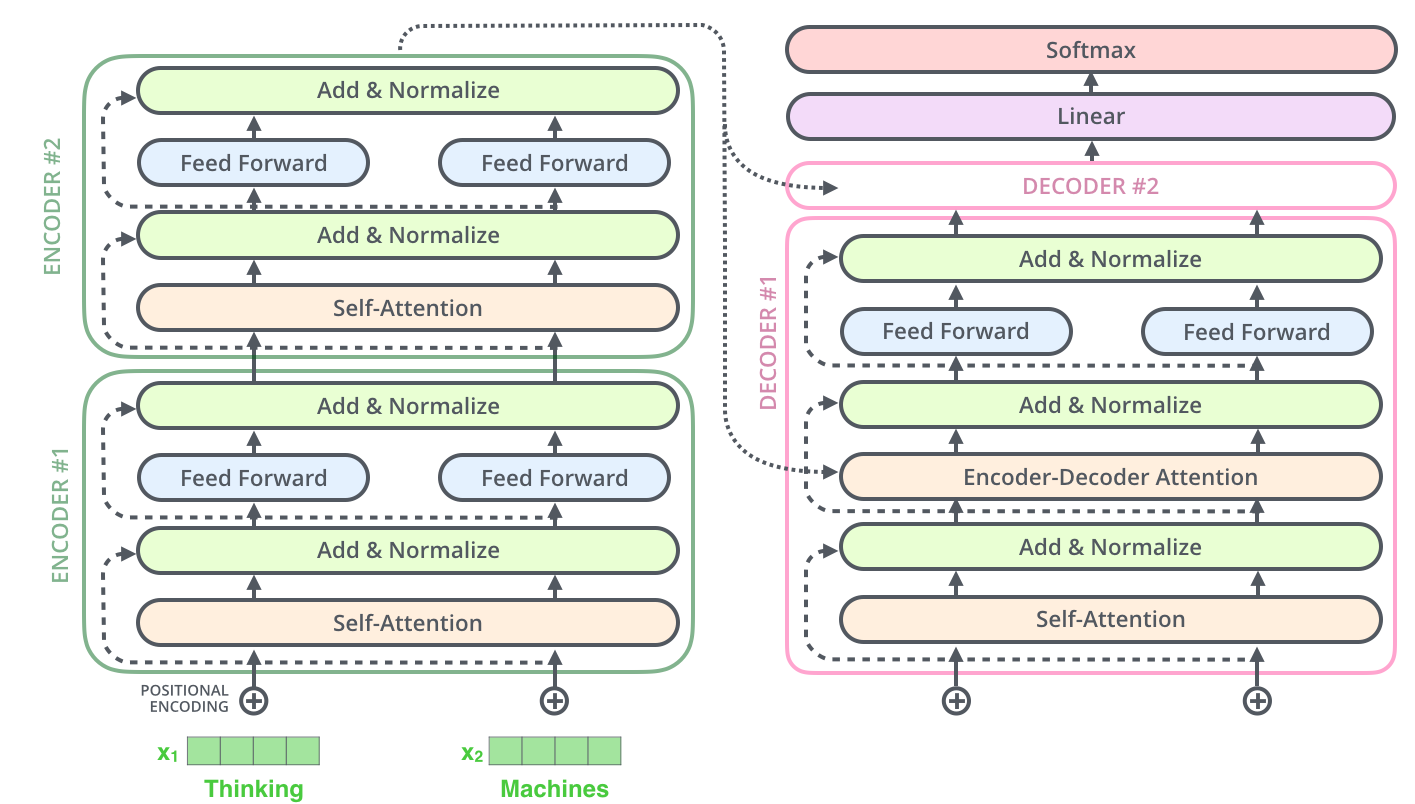
The decoder

encoder self-attn

The decoder

encoder self-attn

The decoder

encoder self-attn

decoder self-attn (masked)

The decoder

encoder self-attn

decoder self-attn (masked)

  • Mask subsequent positions (before softmax)

The decoder

encoder self-attn

context attention

decoder self-attn (masked)

The decoder

encoder self-attn

context attention

  • Use the encoder output as keys and values

$$\mathbf{S} = \mathrm{score}(\mathbf{Q}, \mathbf{R}_{enc}) \in \mathbb{R}^{m \times n} $$

$$\mathbf{P} = \pi(\mathbf{S}) \in \triangle^{m \times n} $$

$$\mathbf{Z} = \mathbf{P} \mathbf{R}_{enc} \in \mathbb{R}^{m \times d}$$

\Bigg\{

decoder self-attn (masked)

$$\mathbf{R}_{enc} = \mathrm{Encoder}(\mathbf{x}) \in \mathbb{R}^{n \times d} $$

The decoder

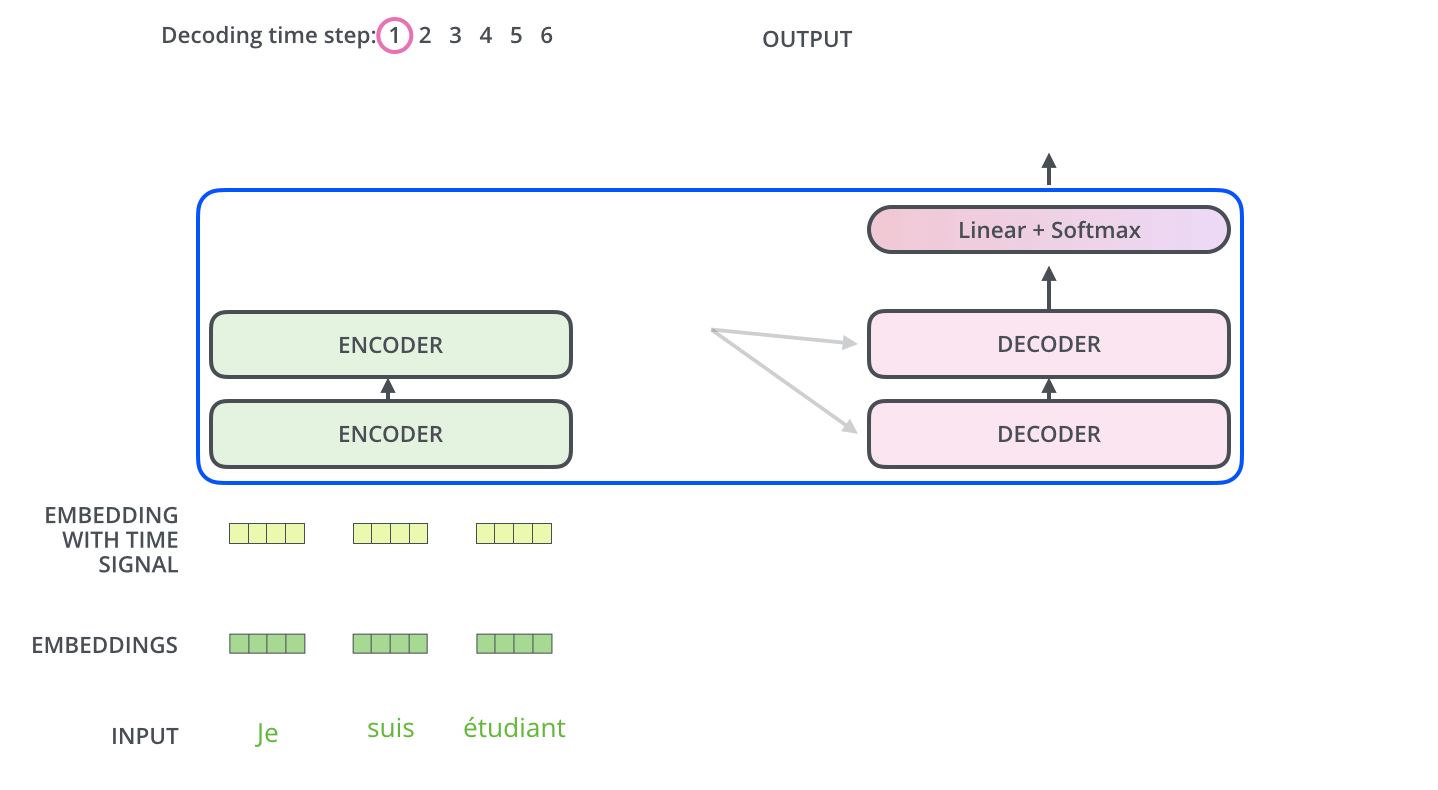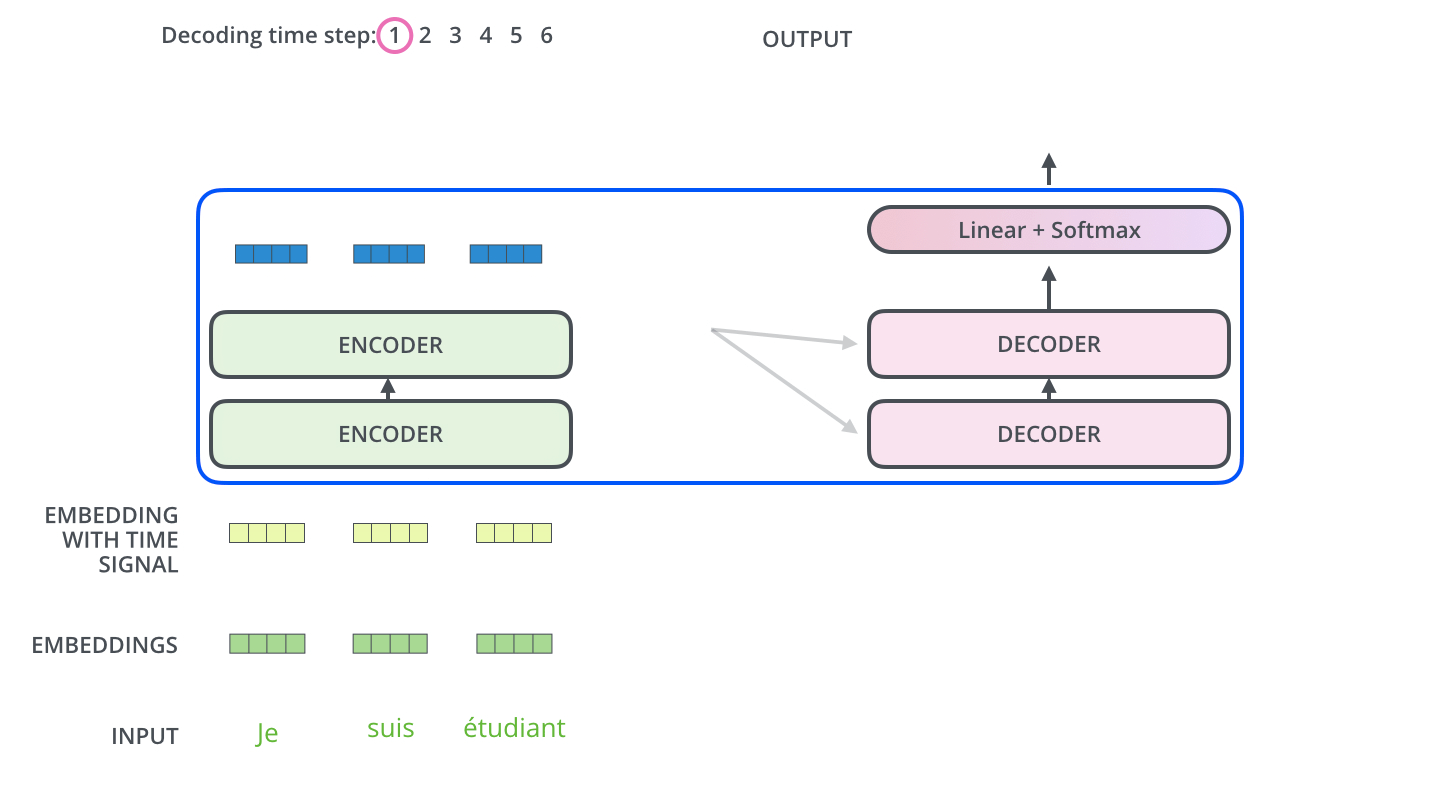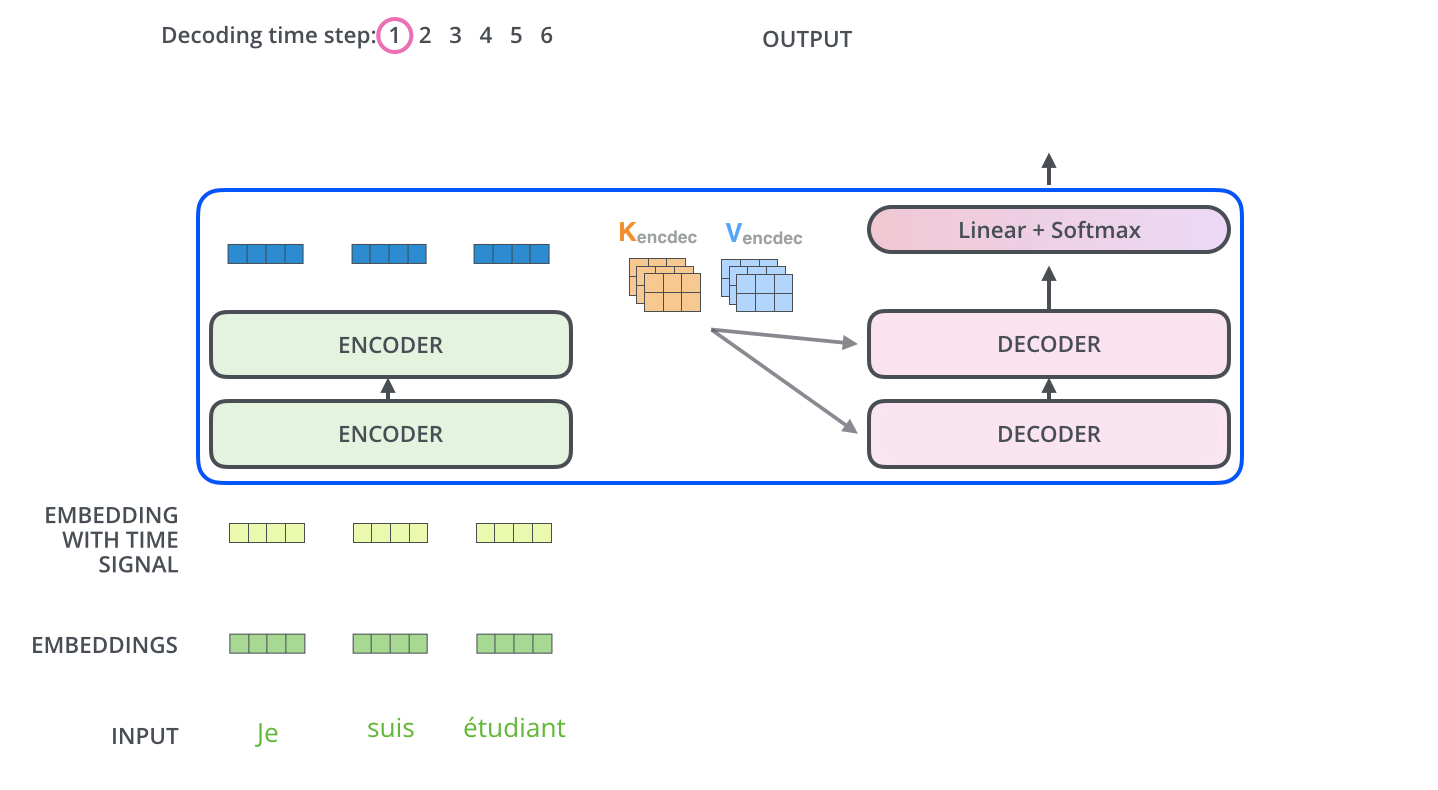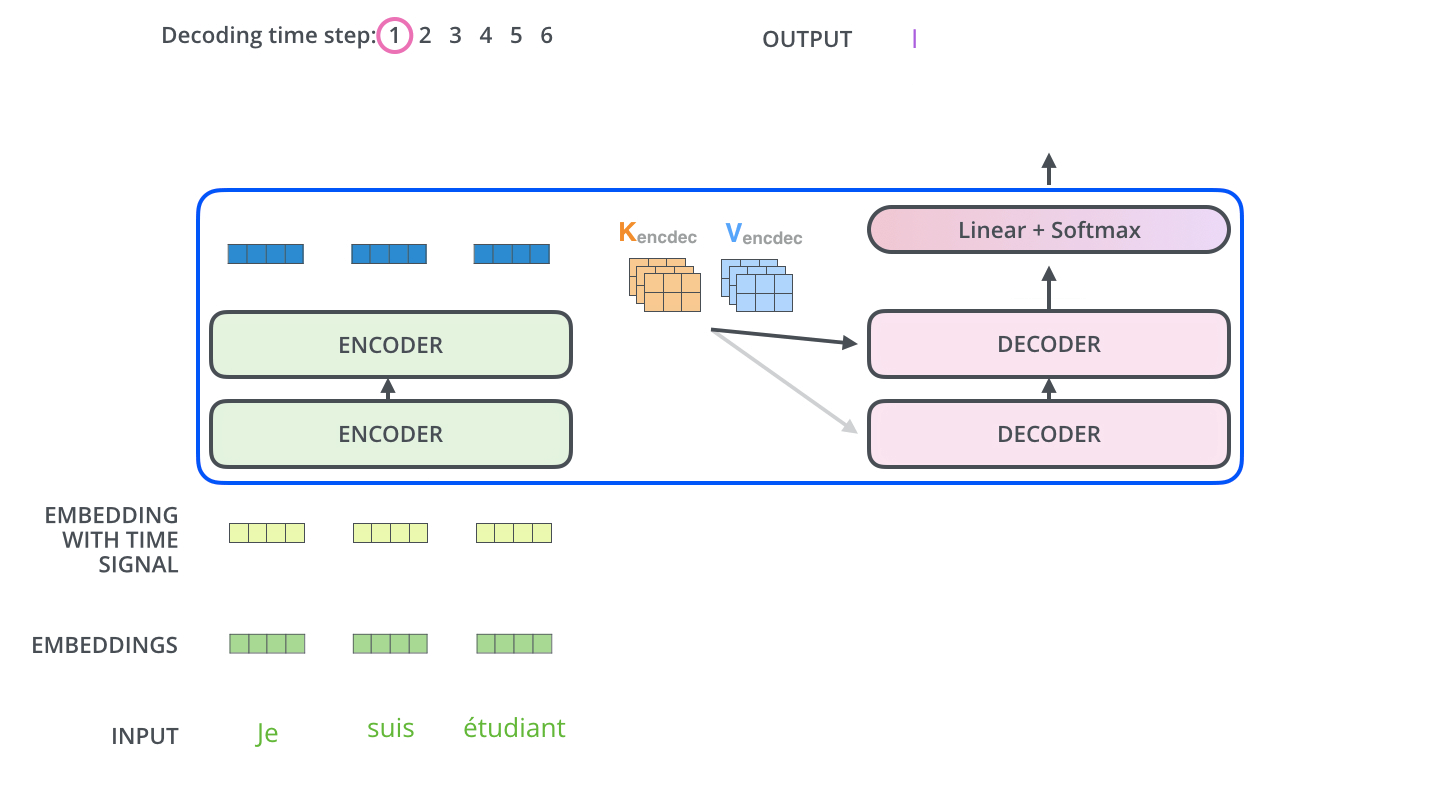
The decoder

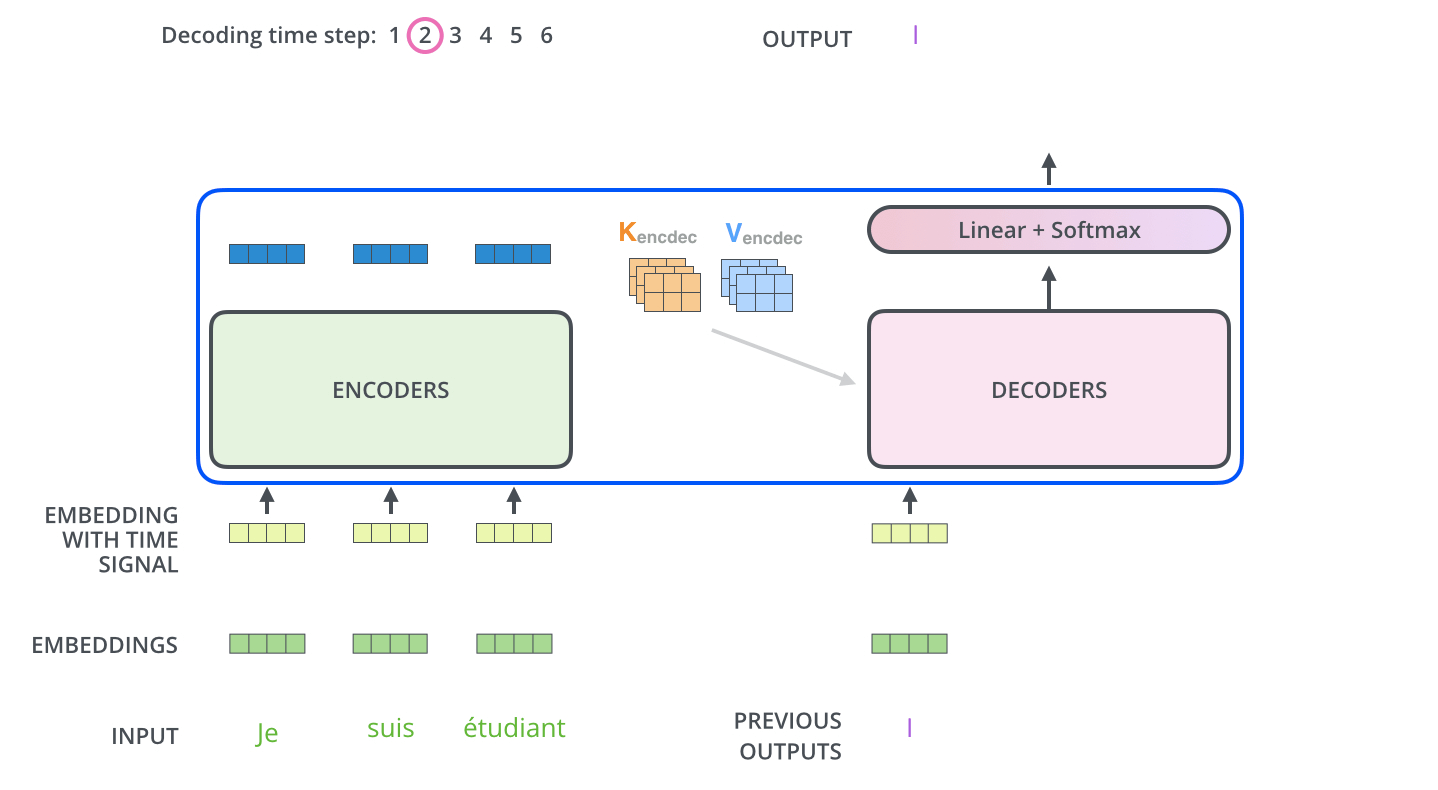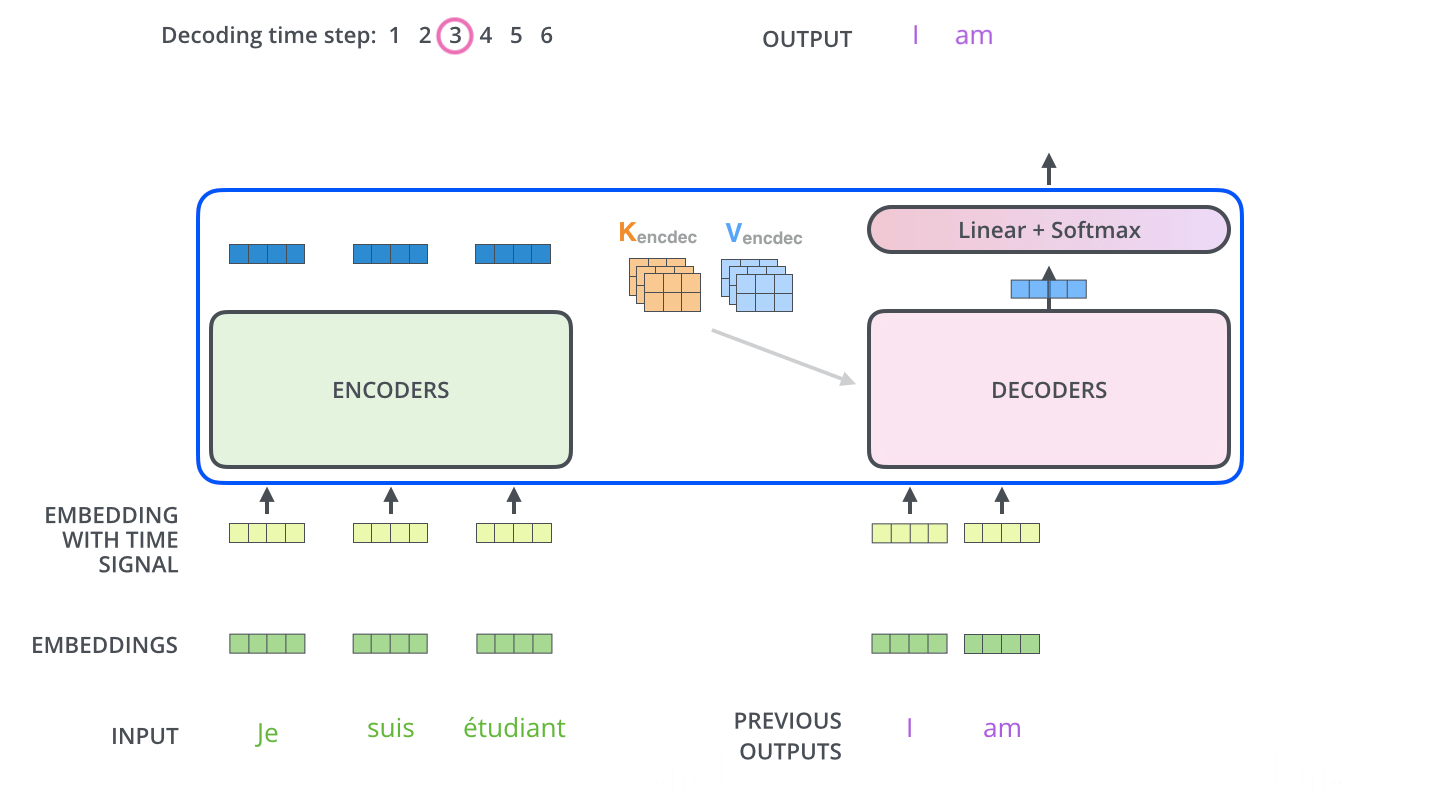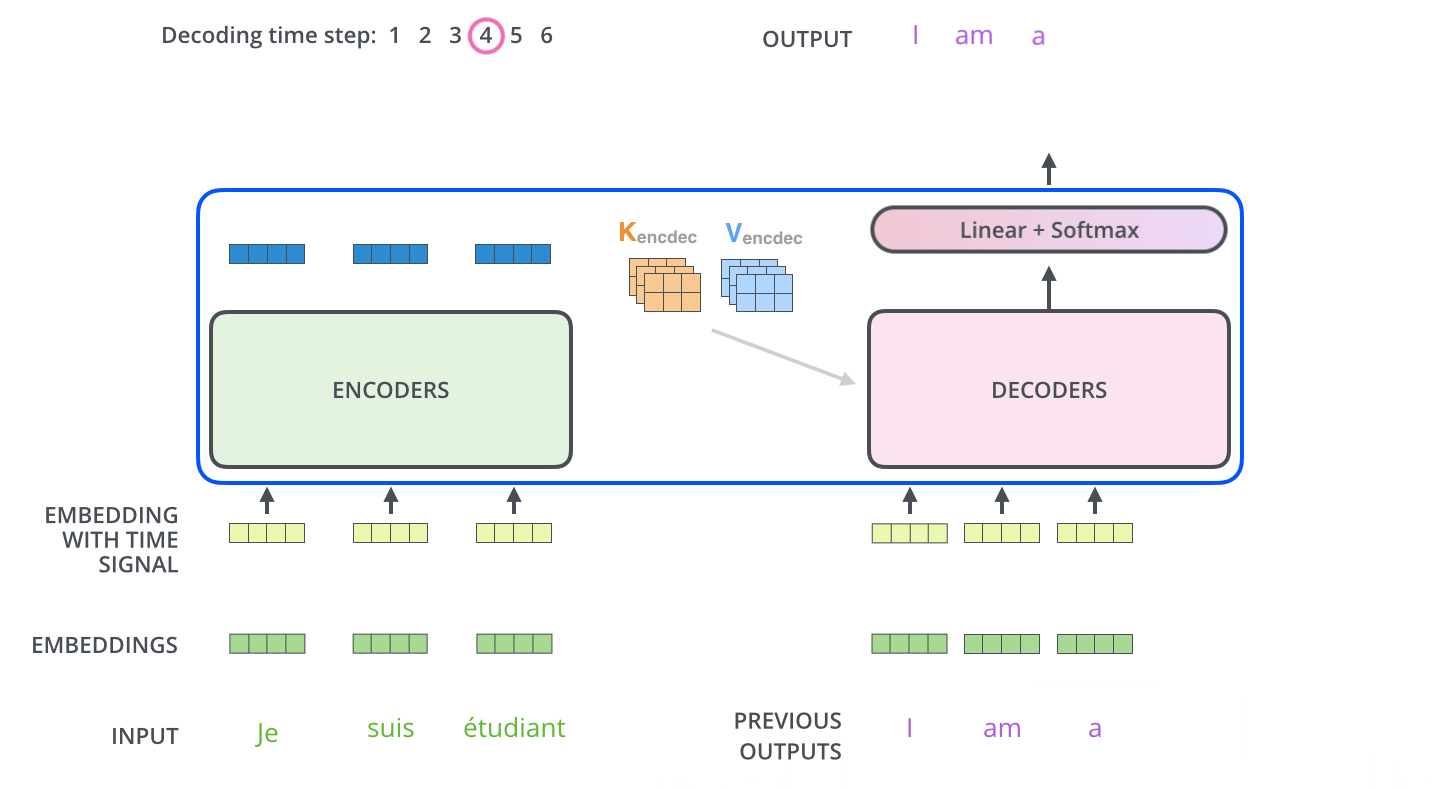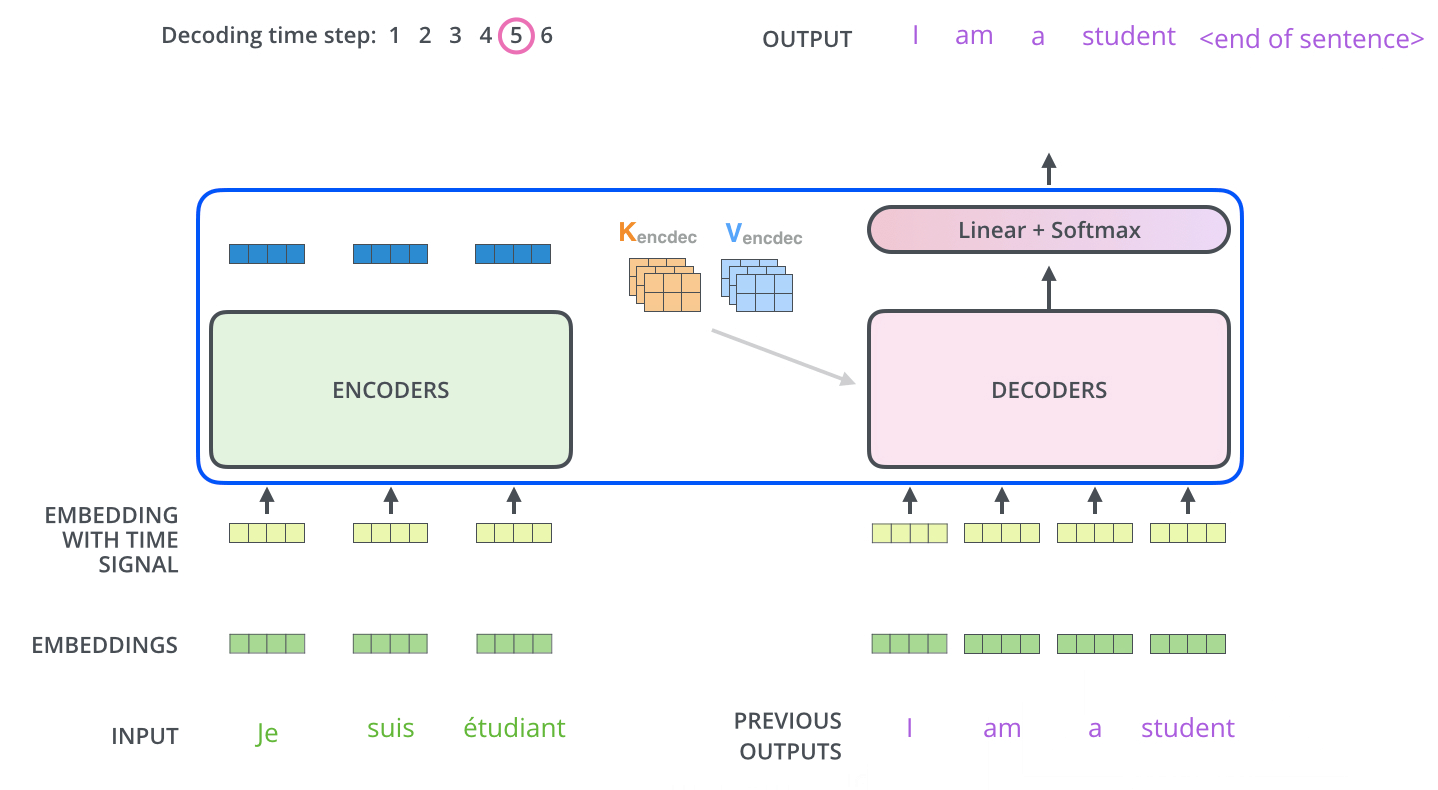
Computational cost

n = seq. length        d = hidden dim       k = kernel size

Other tricks

  • Training Transformers is like black-magic. In the original paper they employed a lot of other tricks:
    • Label smoothing
    • Dropout at every layer before residuals
    • Beam search with length penalties
    • Subword units - BPEs
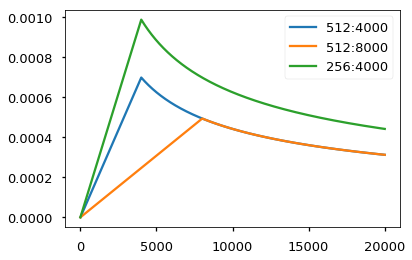
    • Adam optimizer with learning-rate decay

Coding & training tips

What else?

Thank you for your attention!