Quoi ? Quels objectifs ?

Quel bilan ?

Modéliser pour estimer...

Modéliser pour découvrir...

Modéliser pour décider...

Quoi ? Quels objectifs ?

Quel bilan ?

Comment inviter la modélisation dans la construction de compétences de communication orales en mathématiques ?

La modélisation est une des six compétences de la formation mathématique. Elle s’organise autour de choix, notamment :

• les résonances entre des situations réelles et des savoirs mathématiques (abstraction, traduction) ;
• le cadre de la modélisation au regard des données et des connaissances (pertinence, complexification) ;
• l’inventaire des outils disponibles et retenus (stratégie)
• l’élaboration et l’exploration d’un modèle numérique .

Elle s'organise autour de choix successifs, au cœur de l'activité mathématique, dont la verbalisation contribue à sa maîtrise et aux compétences de communication en mathématiques, pour le socle commun et le grand oral.

L'objectif de ce projet TraAM est de construire des activités permettant aux élèves de s'engager dans la narration orale de ces choix

Quoi ? Quels objectifs ?

Quel bilan ?

 

Mode de restitution : Plus motivant.

Plus facile (Monty Hall - Alae, Zaki collège REP+)

 

Travail sur la modélisation : Les activités proposées ont permis de faire des choix de modélisation et de les expliciter

 

Travail sur l'oral : Même si cette dimension a été un peu réduite en raison du contexte sanitaire, les activités permettent des aller-retour permettant à travailler les compétences orales

Estimer la superficie d'une ville

Niveau : 6ème

 

Les élèves doivent estimer la superficie de la ville de Toulouse à l’aide d’un plan qui leur est fourni.

 

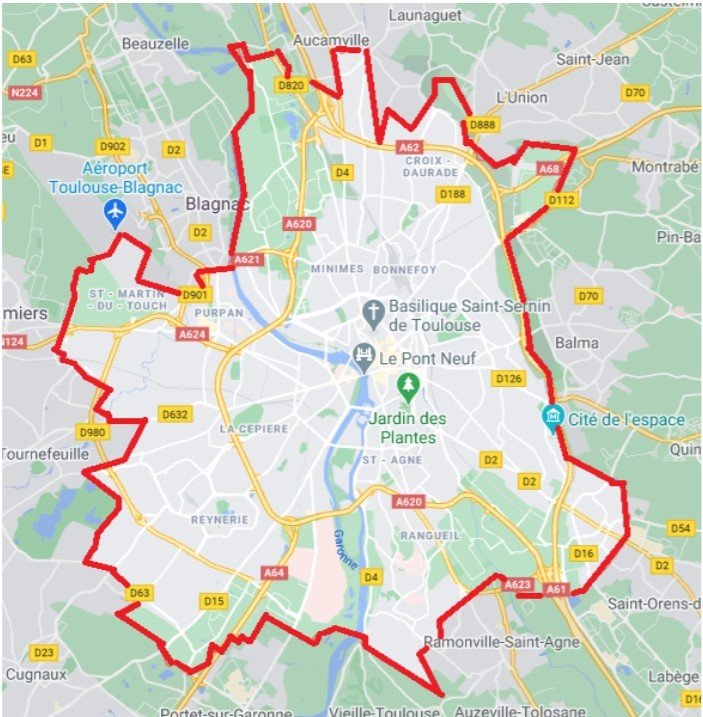
Comment estimer la superficie de Toulouse à l’aide d’un plan fourni ?

Mots clés : modélisation, aire, superficie, précision,grandeur et mesure

 

Objectifs, intentions : Utiliser les formules d’aires au programme (carré, rectangle, triangle et disque).

Déterminer la mesure de l’aire d’une surface à partir d’un pavage simple ou en utilisant une formule.

 

 

Proposer une situation qui puisse donner lieu à des modélisations variées.

Tester les modélisations choisies en confrontant les résultats obtenus et la valeur réelle.

Exercer son esprit critique.

Utiliser l’oral pour argumenter ses choix

Travailler en équipe

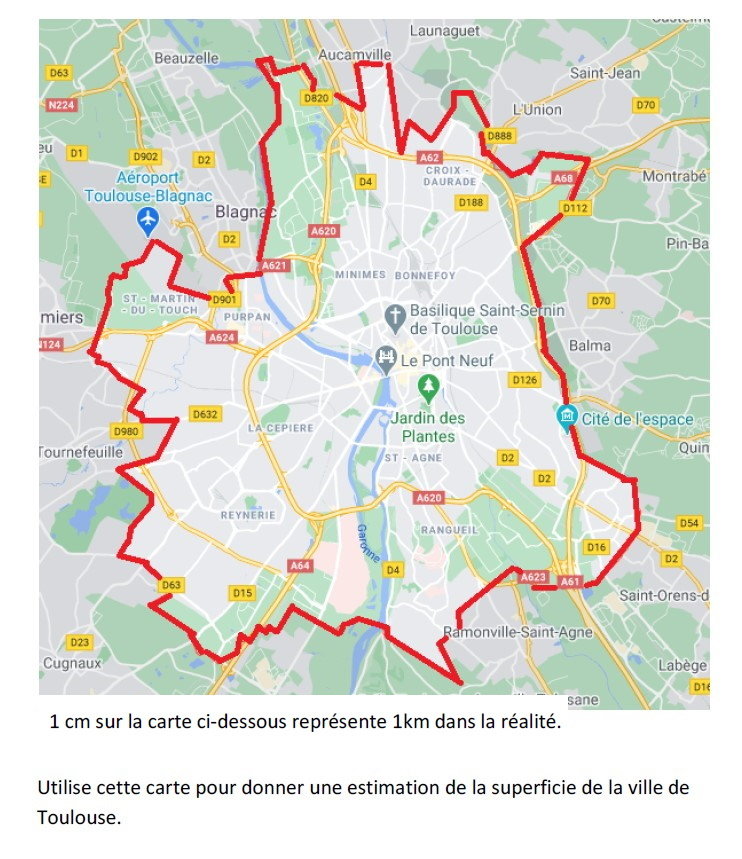
Différencier la tâche et gérer la différence de rapidité en proposant plusieurs plans de villes

Différencier en modifiant l’échelle choisie (ici 1cm pour 1 km).

 

 

 

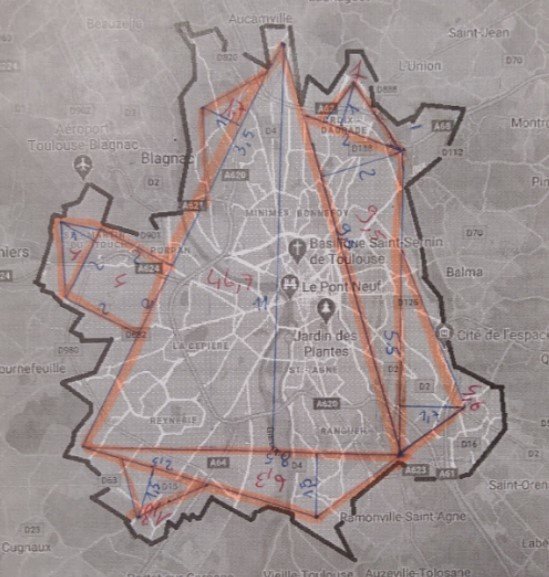
Les productions des élèves

• Groupe 1 : Avec un disque...
• Groupe 2 : Avec des triangles
• Groupe 3 : Avec un quadrillage
• Groupe 4 : Avec des rectangles
• Groupe 5 : Avec des triangles et des rectangles

Accéder à la page

de l'activité

Comment faire sans Google Maps ?

Niveau : 6ème & 4ème

Possible en 5 ème

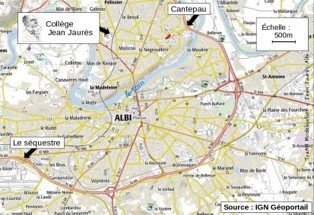
Quelle est la distance entre deux sorties de la rocade d'Albi ?

Il s'agit de déterminer la longueur d’un chemin sur une carte avec des outils élémentaires puis d'évaluer une différence de longueurs non accessible sur Google Maps

Quelle est la distance entre deux sortie de la rocade d'Albi ?

Mots clés : géométrie, ficelle, segment, demi-cercle, longueur étalon,  proportionnalité

 

 

 

 

 

Objectif, intention : Modéliser une situation de la vie quotidienne. La diversité des "outils" proposés permet aux élèves de faire un choix de modélisation entre :

• des reports de longueurs
• l’utilisation d’une ficelle
• l’utilisation de segments de mêmes  longueurs ou de longueurs différentes
• le tracé d’un demi-cercle
• l’utilisation de la proportionnalité

Ce choix est alors explicité à l'oral.

 

Les productions des élèves

Accéder à la page de l'activité

La vidéo des 6ème

La vidéo des 4ème

Tu es sur le point de gagner la partie !

Tu n’as plus qu’à faire rentrer la bille noire en frappant la bille blanche...

Niveau : 4 ème

 

 

 

Quel est le bon tir ?

Encore faut-il déterminer le bon tir !

Comment trouver le bon tir pour rentrer la boule noire en frappant la blanche ?

Niveau : 4 ème

Mots clés : Géométrie dynamique, Algorithmique, Papier/crayon, Loi de Snell-Descartes, Symétrie, Triangles semblables, Échelle

Objectifs et intentions : Modéliser puis choisir un outil (numérique ou non) permettant de répondre au problème.

Travailler la validation du modèle et de la solution en utilisant un vrai billard et ainsi confronté le modèle choisi à la réalité.

 

Communiquer : Verbalisation par les élèves de la démarche, des critères de choix et des avantages/inconvénients respectifs des méthodes mises en œuvre.

 

Plus value de la production d’une vidéo :

Développer les compétences à l’oral

Mobiliser des outils numériques pour échanger, communiquer

 

Trois productions pour trois modélisations différentes

Quel est le bon tir ?

Une réponse "papier crayon"

Une résolution utilisant geogebra

Une résolution avec Scratch

Aller à la page de l'activité

N'y a-t-il que les idiots qui ne changent pas d'avis ?

Niveau : 4 ème

Adaptable en 3 ème et en lycée avec des objectifs différents

 

 

 

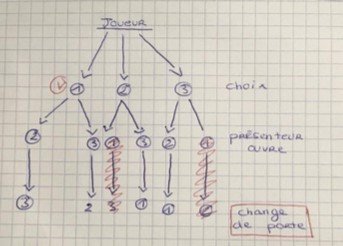
Le paradoxe de Monty  Hall

A-t-on autant de chance de gagner au jeu de Monty Hall quelle que soit sa stratégie ?

Niveau : 4 ème

 

Mots clés : Jeu, Probabilités, Algorithmique, Travail de Groupe

 

Objectifs et intentions : Modéliser Choisir une modélisation permettant de reproduire la situation du jeu en classe. On pourra ensuite travailler l’approche fréquentielle des probabilités et aborder pour la première fois une approche plus théorique de celles-ci. Afin d'effectuer un maximum de simulations, les élèves doivent choisir un outil adapté.

 

Communiquer : Ces choix sont explicités oralement.

 

Le choix de l'outil (mise au point plus ou moins autonome d'un programme scratch ou expérimentation "à la main") permet la différentiation.

 

 

 

 

Compétences mathématiques travaillées :

• Modéliser : Modéliser pour résoudre des problèmes concrets - Utiliser, comprendre, élaborer une simulation
• Communiquer : Communiquer pour expliquer (communication orale)
• Chercher : S’engager dans une démarche, expérimenter, émettre une conjecture -

Tester, essayer, valider, corriger une démarche (engagement favorisé par le côté ludique)

• Représenter : Représenter pour résoudre des problèmes (organigramme)

 

Axes de modélisation :

• Comment modéliser la situation par un jeu praticable en classe ?

• Modélisation du jeu à “grande échelle” (scratch)
• Choix de l’outil pour effectuer un maximum de simulation (Plus-value de l’informatique)           

 

A-t-on autant de chance de gagner au jeu de Monty Hall quelle que soit sa stratégie ?

A-t-on autant de chance de gagner au jeu de Monty Hall quelle que soit sa stratégie ?

Commentaires :

• Travail par groupes pré-établis où l’engagement, qui est favorisé par l’aspect ludique, a permis à certains élèves de révéler des compétences qu’ils ne montrent pas habituellement;
• L’oral permet à certains de débloquer des difficultés qu’ils ont à l’écrit;
• Mise en avant de la plus-value inégalable de la création du programme de simulation “scratch” par rapport à la simulation avec des cartes à jouer.

 

Prolongement possible : Imaginons une nouvelle version du jeu, avec quatre portes, une voiture derrière l’une d’elles, des ânes derrière les autres. Le présentateur joue le même rôle que dans la version précédente.

Les productions

des élèves

• Explications du jeu
• Modélisation
• Oral
• Difficultés

Accéder à la page

de l'activité

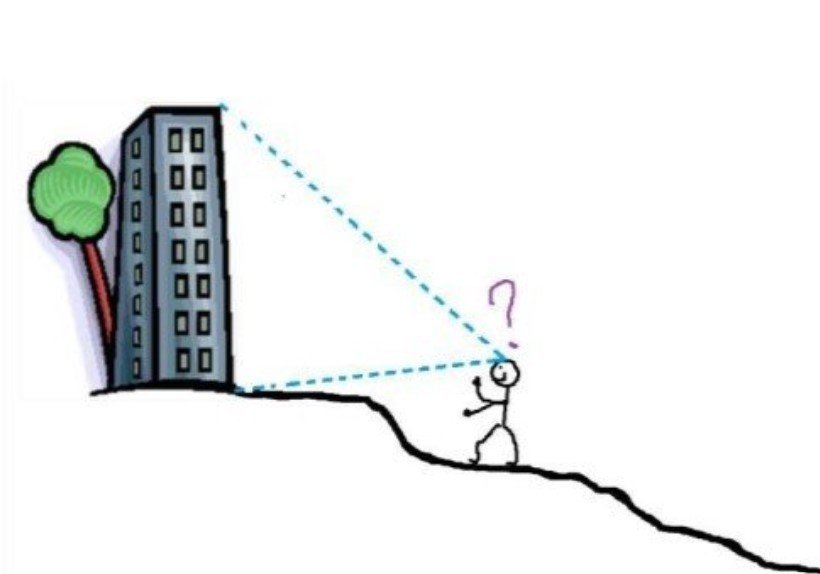
Comment estimer précisément la hauteur du bâtiment principal du collège, malgré les fortes contraintes topographiques du lieu avec une surface non plane ?

Niveau : 4 ème ou 3 ème

 

 

 

 

Mais combien mesure le collège ?

Comment estimer précisément la hauteur du bâtiment du collège, malgré les contraintes topographiques du lieu avec une surface non plane ?

Niveau : 4 ème ou 3 ème

Mots clés : Grandeurs inaccessibles, triangles semblables, surface non plane, travail interdisciplinaire, esprit critique, précision, outils de bricolage, géométrie dynamique

Objectifs, Intentions : Utiliser les notions vues sur les triangles semblables pour introduire le théorème de Thalès

Faire le lien entre la proportionnalité et la configuration géométrique présente (triangles semblables, agrandissement-réduction)

 

Développer des stratégies de modélisation (traduire en langage mathématique une situation réelle à l’aide d’une configuration géométrique)

Exercer son esprit critique pour écarter les stratégies qui ne peuvent aboutir

Utiliser l’oral pour argumenter ses choix

 

Les productions des élèves

• Vidéo 1
• Vidéo 2
• Vidéo 3

Accéder à la page de l'activité

Le robot tourmenté

Niveau : Terminale

Possible dès la seconde

 

 

 

 

 

R2 est un robot tourmenté : son système d’exploitation lui joue des tours et bouleverse sa trajectoire en direction des bases de rangement. A chaque changement de trajectoire, R2 laisse une trace sur le sol. Au bout d’un certain temps, lorsque l’on regarde du ciel, une étrange figure apparaît. Saurez-vous la reconnaître ?

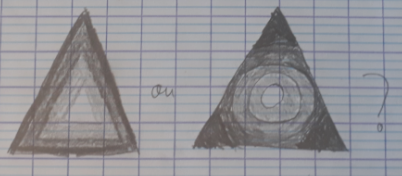
Le robot tourmenté

Mots clés : Programmation – Géométrie repérée – Hasard – Fractale

 

Objectifs, Intentions : Proposer aux élèves une situation dans laquelle ils peuvent s'engager facilement et le résultat final est inattendu et impressionnant.

On travaille la modélisation.

On mobilise la distance entre deux points dans un repère orthonormé et l'algorithmique et programmation  (simuler le hasard, boucles, représentation graphique …)​.

 

Plusieurs outils numériques peuvent être utilisés. Les élèves font alors un choix qu'ils explicitent à l'oral. On travaille ainsi l'argumentation.

 

 

 

 

Le robot tourmenté

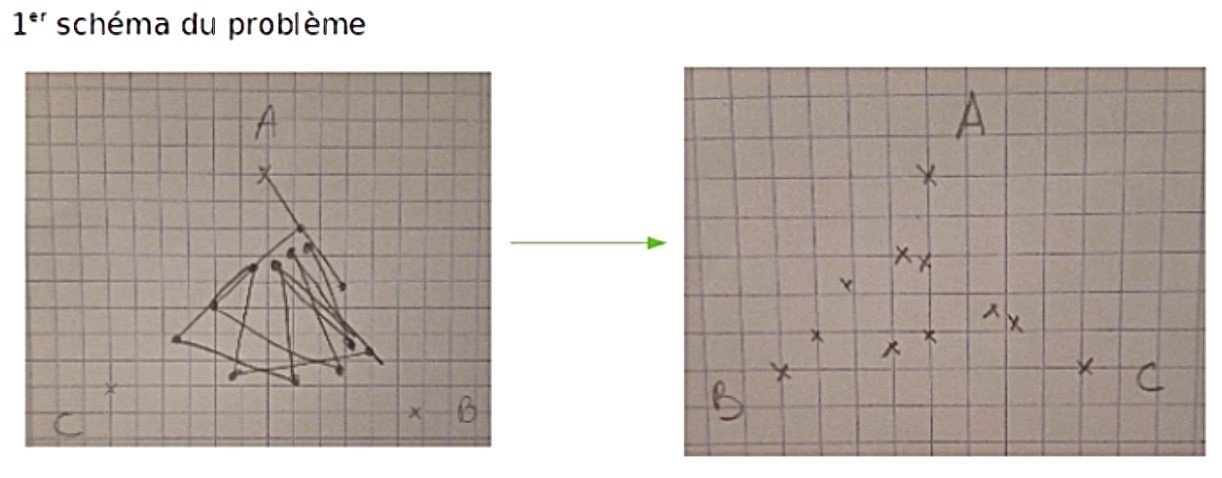
Axes de modélisation :

• Comment modéliser la situation ? (quelle figure géométrique?)
• Géométrie repérée ou non ? Triangle – distance entre deux points
• Choix de l’outil pour tracer un nombre important de points: python, scratch, géométrie dynamique, tableur

 

Commentaires :

Ce problème offre la possibilité de faire facilement une première modélisation « à la main » de la situation ou en utilisant un logiciel de géométrie dynamique en simulant le hasard … au hasard (c’est celui qui fait la figure qui décide au hasard de la direction du robot.)

Cela devient vite laborieux et il n’apparaît pas grand-chose « vue du ciel ».

Se pose alors la question de l’outil numérique permettant de simuler au mieux la situation.

Plusieurs possibilités : Scratch, Python, tableur, logiciel de géométrie dynamique
 

Prolongements possibles :

• La position du robot (dans le triangle et/ou en dehors du triangle) a-t- elle une incidence sur le résultat obtenu ?
• Si le nombre de bases de rangement est supérieur à 3, retrouve-t-on une figure du même type ?

Les productions des élèves

• Vidéo 1
• Vidéo 2
• Vidéo 3
• Vidéo 4

Accéder à la page de l'activité

Jurassic Park

Niveau : Terminale EDS

 

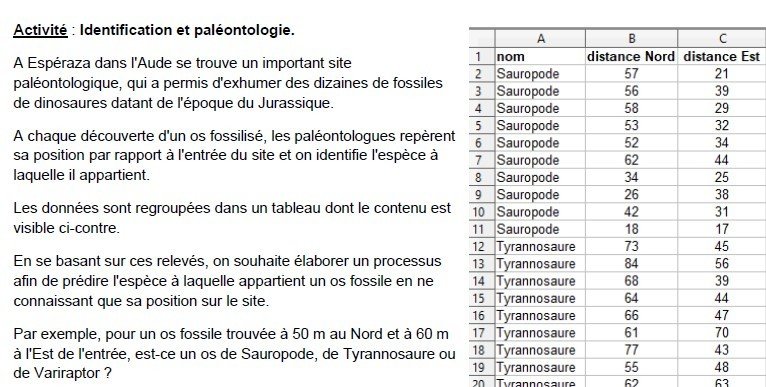
Identification et paléontologie :

A Espéraza dans l'Aude se trouve un important site

paléontologique qui a

permis d'exhumer des

dizaines de fossiles de

dinosaures datant de

l'époque du Jurassique.

 

 

 

Jurassic Park

Mots clés : python, algo k plus proches voisins,

Programmation Géométrie repérée

 

Objectifs, Intentions : Découverte d’un algorithme
de e-learning : algo des k plus proches voisins.

 

Utiliser une simulation numérique pour modéliser.

 

On mobilise la distance entre deux points dans un repère orthonormé ou module d’un nombre complexe. 

On travaille l'algorithmique et programmation (boucles, tests, listes, ...) ou l'utilisation d'outils numériques (tableur, géogébra)

 

Les élèves proposent et ont choisi des méthodes variées : différentes distances, différents choix de rayons, différentes zones. Ils explicitent ces choix à l'oral.

 

Le grand nombre de données fournies par l’énoncé les invite à avoir recours à l’outil numérique, qui va permettre de traiter ce grand nombre de données rapidement. 

Lire la suite

Jurassic Park

 

Commentaires :

De par la nature de son thème (fouilles paléontologiques),

l’activité invite assez naturellement les élèves à représenter dans un repère chaque ossement dont les coordonnées sont précisées dans l’énoncé. Ils remarquent alors des zones dans lesquelles les ossements de chaque espèce sont regroupées et vont alors réfléchir à comment déterminer l'espèce d'un os en comparant avec la position des os voisins.

Premier temps (1 heure) : Dans un premier temps, regroupés par 2 ou 3, les élèves ont découvert la problématique et échangé leurs idées pour élaborer une méthode pour répondre au problème posé.

Second temps (2 heures) : Ils ont modélisé leur méthode à l’aide d’un programme informatique.

Dernier temps (hors classe), ils ont conçu en autonomie la capsule vidéo demandée avec les outils présentés dans le document ou, pour certains, des logiciels avec lesquels ils avaient l’habitude de travailler

 

Les productions des élèves

• Vidéo 1
• Vidéo 2
• Vidéo 3

• Vidéo 1
• Vidéo 2
• Vidéo 3

Accéder à la page de l'activité

Ils trichent ! 

Niveau : Terminale Générale en Enseignement Commun Scientifique

Problématique de modélisation adaptable aux différents niveaux du lycée en modifiant les modèles attendus.

Activité  : Depuis le temps que ça dure, j’en suis quasiment certain. Je n’ai presque jamais la fève ! A tous les coups, ma famille triche. Il ne me reste qu’à le prouver… mais comment faire ?

L'activité est prévue en trois phases progressives. Cela permet des aller-retour grâce auxquels on  précise la modélisation et on travaille l'oral.

Ils trichent ! 

Mots-clefs : probabilité, statistique, inférence bayésienne, simulation, esprit critique.

 

Objectifs, Intentions :
• Modélisation par 3 modèles avec comparaison
• Éclairer le lien entre probabilité et statistique (thème Biodiversité)
• Introduire l’inférence bayésienne (thème I.A)
• Démarche formative sur plusieurs vidéos

Plus-value de la production d’une vidéo :
• Préparation du grand oral
• Accès aux préconcepts des élèves
• Différentiation simple à mettre en œuvre
• Travail sur la précision du vocabulaire

Les productions des élèves en 3 étapes

Etape 1  :  Un travail de modélisation mais sans indication (pour partir de leurs pré-concepts)

            Vidéo 1 : Elève suivant l'option maths complémentaires           

            Vidéo 2 : Elève suivant l'option maths expertes

Etape 2 : La même question mais en ayant fixé deux cadres de modélisation (avec les hypothèses retenues)

           Vidéo 1 : Elève suivant l'option maths complémentaires

           Vidéo 2 : Elève suivant l'option maths expertes

           Vidéo 3 : Elève suivant l'EDS mathématiques

Etape 3 : Toujours sur la même question mais éclairée par un contenu nouveau (l'inférence bayésienne). Non mis en oeuvre

Accéder à la page de l'activité

Le docteur Grey a besoin de vous !

Niveau : Terminale

 

 

 

 

Activité  : Dosage d'un analgésique.

Trois modélisations sont suggérées ; les élèves doivent choisir l'une d'elle et motiver ce choix

 

 

 

 

Le docteur Grey a besoin de vous !

Mots clés :  Ajustement affine, équations différentielles,

suites, argumenter 

Objectifs, Intentions :

Modéliser consiste souvent à choisir un modèle. Cette

activité présente plusieurs pistes de modélisation (ajustement

affine, suites numériques, équations différentielles) . Les

élèves doivent les explorer puis choisir celle qui leur semble la plus pertinente. Ils explicitent ensuite leurs choix à l'oral.

 

Commentaires : L’activité a été testée dans une classe très hétérogène. Les différents axes proposés ont permis à tous les élèves de répondre à la question a minima en utilisant un ajustement affine.

Quelques productions

élèves

• Vidéo 1
• Vidéo 2
• Un témoignage 

Accéder à la page de l'activité