

- Student's Portfolio
- Accepted First Author Papers
- First Author Papers - Under Review
- Collaboration (co-author) Papers - Under Review
- Course Instructor Experience
- RNNs, Transformers, Diffusion Models - Recap
- Paper 1: Large Language Diffusion Model
- Takeaways for future research in this area
- Paper 2: Immiscible Diffusion - Accelerating Diffusion Training.
- Paper 3: State Space Models, Mamba and LinOSS
- Q & A
\( \text{Contents of this Presentation:}\)

- Enhancing Privacy and Control in Generative Models
- Focus: Text to Image Diffusion Models
- Projects:
- ICCV 2025: Watermarking AIGC.
- ACM MM 2025: Unlearnable Sample Generation.
- NeurIPS 2025: Controlling hallucinations in Diffusion Models.
- NeurIPS 2025: Mitigating Catastrophic forgetting in LDMs.
- WACV 2026: De-biasing Latent Diffusion Models.
\( \text{Theme of Research so far:}\)
Accepted first author paper in BOLD.

\( \textbf{Your Text Encoder Can Be An Object-Level Watermarking Controller}\)
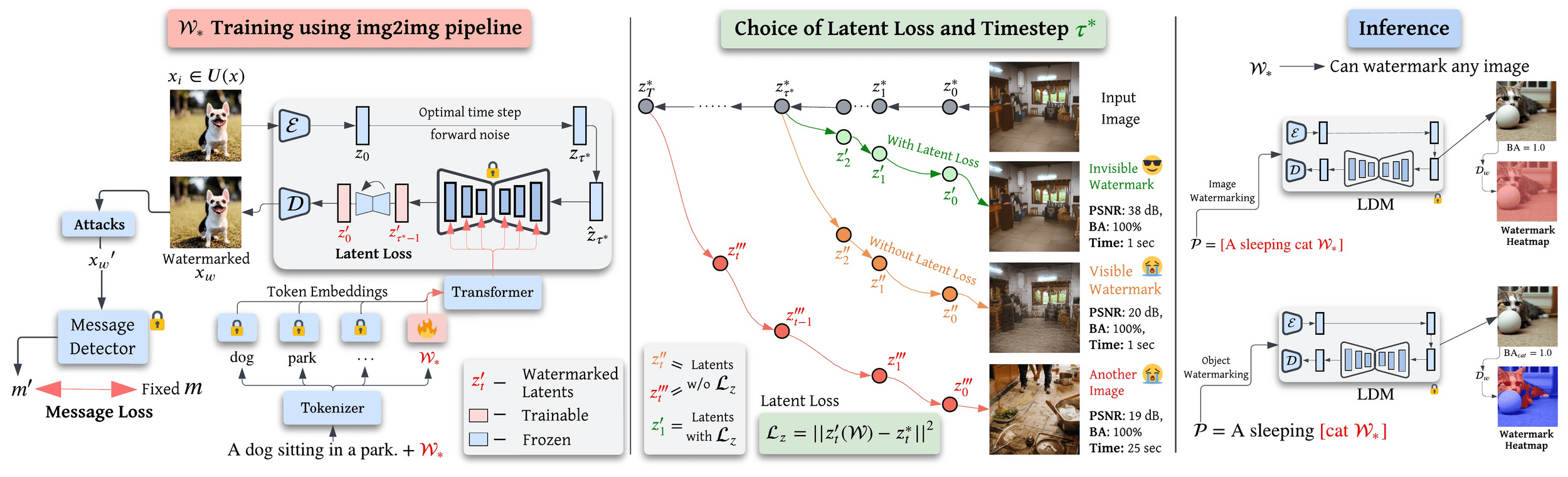

Train Single Token Text Embeddings for Watermarking

\( \textbf{Your Text Encoder Can Be An Object-Level Watermarking Controller}\)

Latent Loss for Minimal Trajectory Adjustment to enable imperceptible watermarking

\( \textbf{Your Text Encoder Can Be An Object-Level Watermarking Controller}\)

Same Token Embedding can be used for both Full-image and Object-Level Watermarking
(utilizing Cross-Attention Maps)

\( \textbf{Your Text Encoder Can Be An Object-Level Watermarking Controller}\)


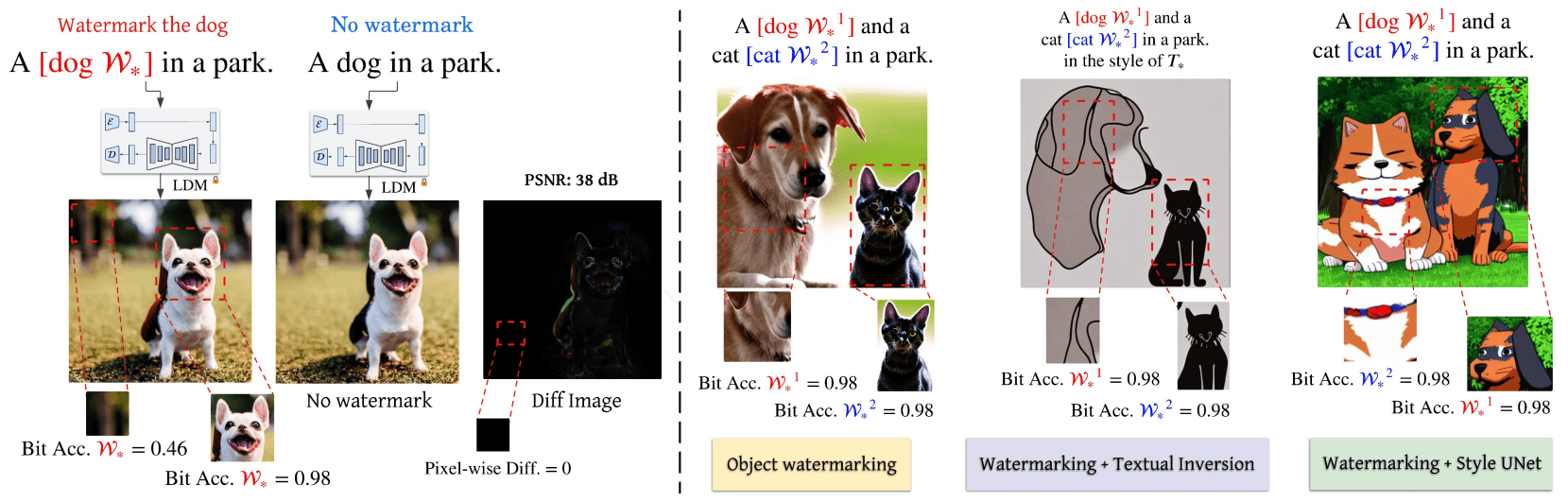



\( \textbf{Personalization through Trajectory Shifted Perturbations}\)
\( \textbf{Latent Diffusion Unlearning: Protecting against Unauthorized}\)

Shift Start of the Diffusion Denoising Trajectory for Latent-Level Unlearnable Sample.


\( \textbf{Personalization through Trajectory Shifted Perturbations}\)
\( \textbf{Latent Diffusion Unlearning: Protecting against Unauthorized}\)
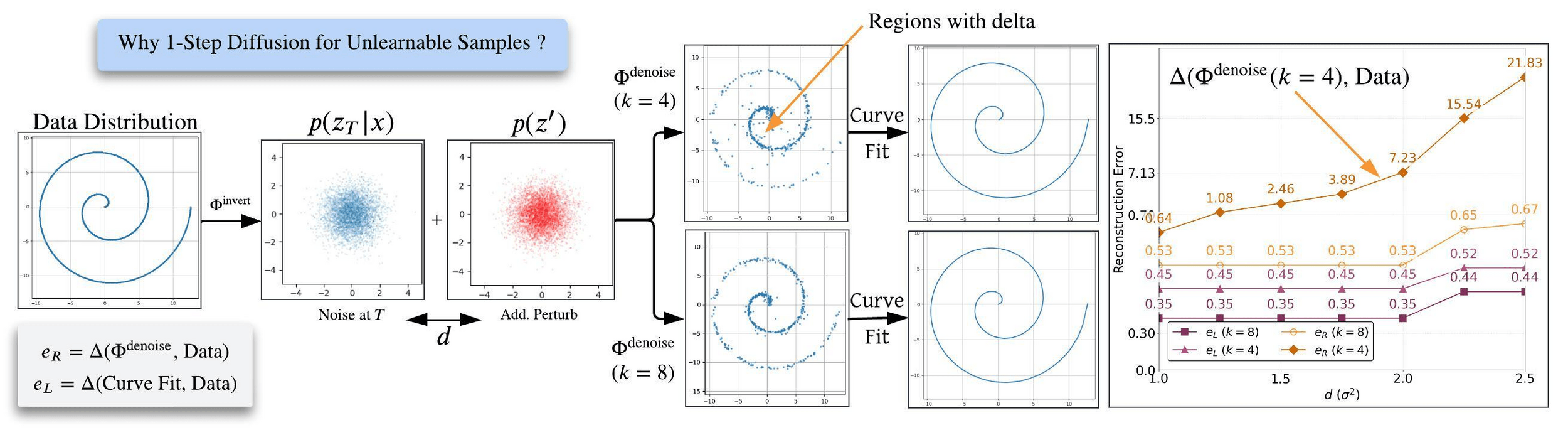
Shortcut Diffusion Models for Unlearnable Perturbation Propagation

\( \textbf{Personalization through Trajectory Shifted Perturbations}\)
\( \textbf{Latent Diffusion Unlearning: Protecting against Unauthorized}\)
Artifact-Free
Unlearnable Samples

Visible Perturbation Overlay

\( \textbf{Personalization through Trajectory Shifted Perturbations}\)
\( \textbf{Latent Diffusion Unlearning: Protecting against Unauthorized}\)

Resistance to Strong DiffPure Attack

\( \textbf{Submitted First Author Papers - Under Review:}\)
\( \textbf{Controlling Hallucinations in Diffusion Models: A Case Study on Chess}\)
Mahesh Bhosale*, Naresh Kumar Devulapally*, Abdul Wasi Lone, Vishnu Suresh Lokhande, David Doermann
\( \textbf{Submitted to NeurIPS 2025:}\)
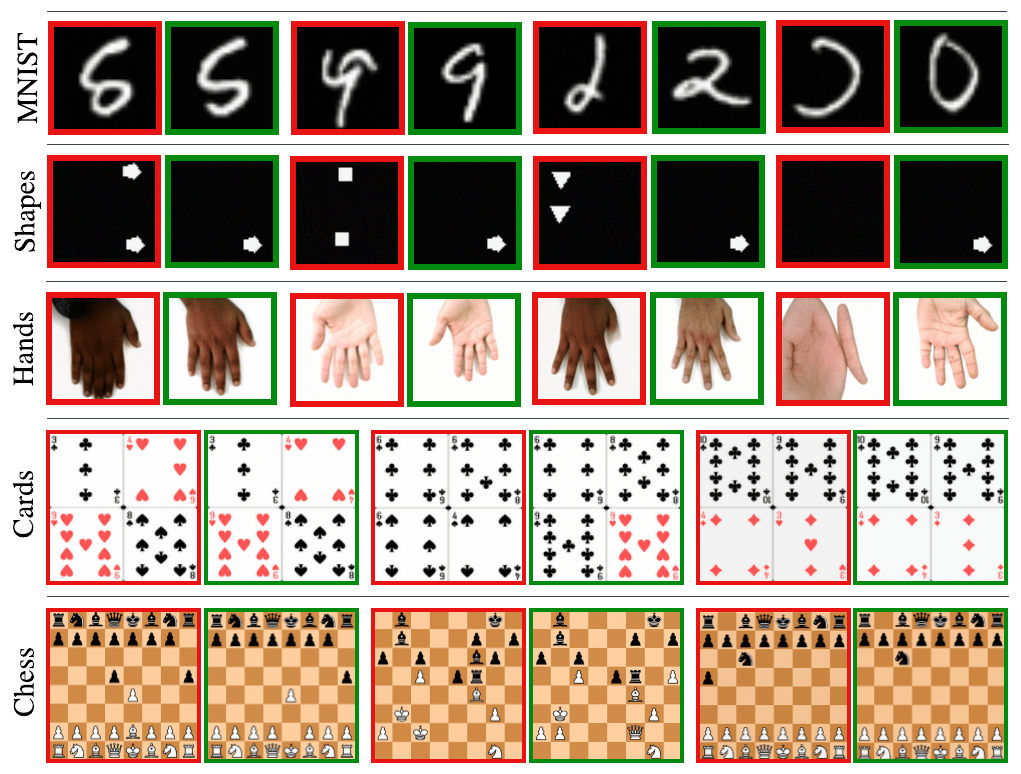
Variance Learning
and
Score Amplification
for
Hallucination Reduction

\( \textbf{Teaching Experience:}\)
\( \text{Course Instructor:} \textbf{ Computer Vision and Image Processing}\)
\( \text{Summer - 2025} \)
\( \text{Number of Students: } \textbf{71}\)
\( \text{Variational AutoEncoders} \)
\( \text{Diffusion Models}\)
\( \text{Generative Adversarial Networks}\)
\( \text{Reading Group Summer 2025} \)
\( \text{Discuss Recent GenAI papers}\)
\( \text{PhD Students at UB}\)




- Large Language Diffusion Models
- ArXiV Preprint
- Accelerating Diffusion Training with Noise Assignment
- NeurIPS 2024
- Oscillary State-Space Models and Mamba
- ICLR 2025 (Oral)

Generative Modeling Principles
unknown
• Generative modeling aims to learn a model \( p_\theta(x) \) that closely matches the real data distribution \( p_{\text{data}}(x) \) by minimizing their KL divergence or equivalently maximizing log-likelihood.

Forward Diffusion
Reverse Diffusion
Training via ELBO
Noise Matching Term

Training via ELBO
Noise Matching Term

Training via ELBO
Noise Matching Term
Parallel Decoding
Fixed-Time Sampling

Autoregressive Formulation in Traditional LLMs
Each token prediction depends on previous tokens.
Sequential sampling
No parallelism
Error compounding
Sequential sampling

Is the autoregressive paradigm the only viable path to achieving the intelligence exhibited by LLMs?
Research Question:

Large Language Diffusion Models
Pre-training
Supervised Finetuning
Sampling

Large Language Diffusion Models - Contributions
- Scalability
- In-Context Learning
- Instruction-Following
- Reversal Resoning
- Outperforms GPT-4o

Large Language Diffusion Models - Loss
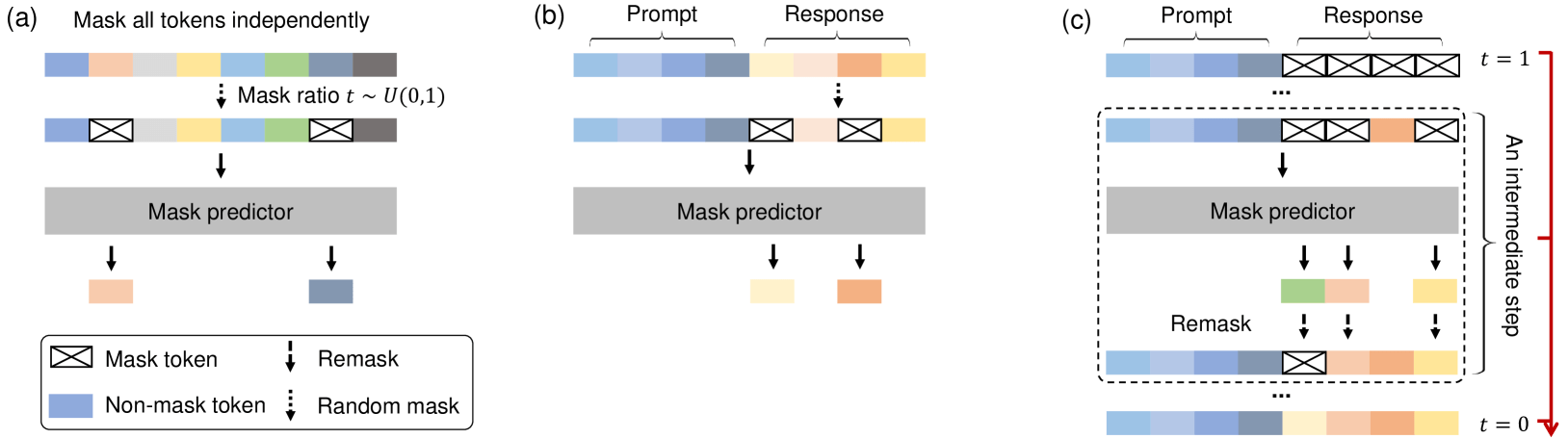
LLaDA’s core is a mask predictor: a model \( p_\theta(\cdot \mid x_t) \) that takes a masked sequence \( x_t \) and predicts all masked tokens (set \( M \)) simultaneously.
Pre-trained on 2.3 trillion tokens took 0.13 milion H800 GPU hours.

Large Language Diffusion Models - SFT Loss
\( L' \) - dynamic length response.

Large Language Diffusion Models - Inference
Initialization: The input sequence is constructed as [prompt tokens] + [MASK tokens] of target length.
Block-wise Iterative Denoising: The generation proceeds block-by-block. At each step, the model predicts logits for all masked positions in the current block.
Confidence-based Remasking Loop: This denoising loop is repeated for a fixed number of steps. Enables parallel yet progressive refinement of the full sequence.

Evaluation Metrics
- Scalability - (FLOPs v/s Performance)
- In-Context Learning - (Few-shot accuracy curves)
- Instruction-Following - (Supervised Fine-Tuning (SFT) accuracy)
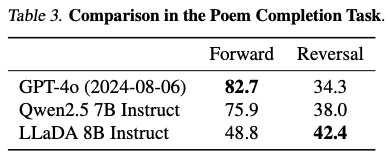
- Reversal Reasoning - Poem Completion Task
- Outperforms GPT-4o

Scalability
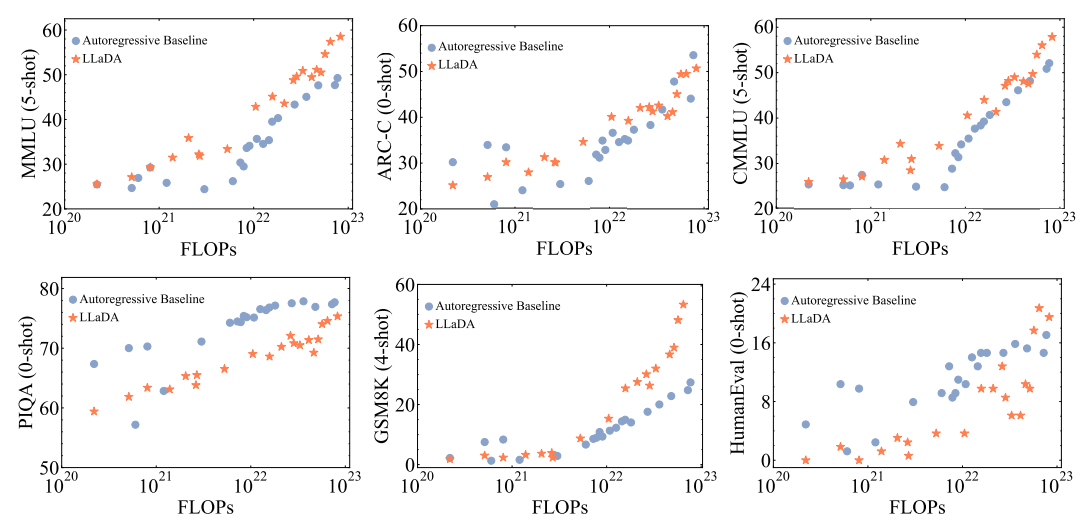

Performance compared to baselines
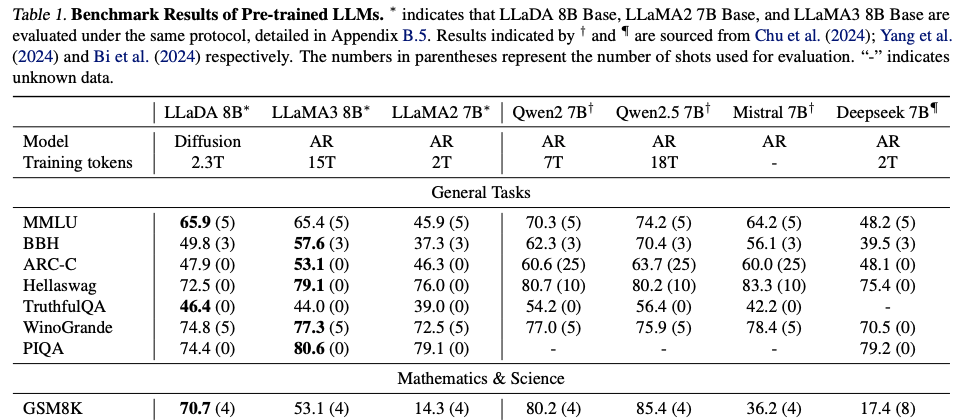

Reversal Reasoning

Limitations: Inference Time (No KV Caching)

Accelerating Diffusion Large Language Models with SlowFast Sampling



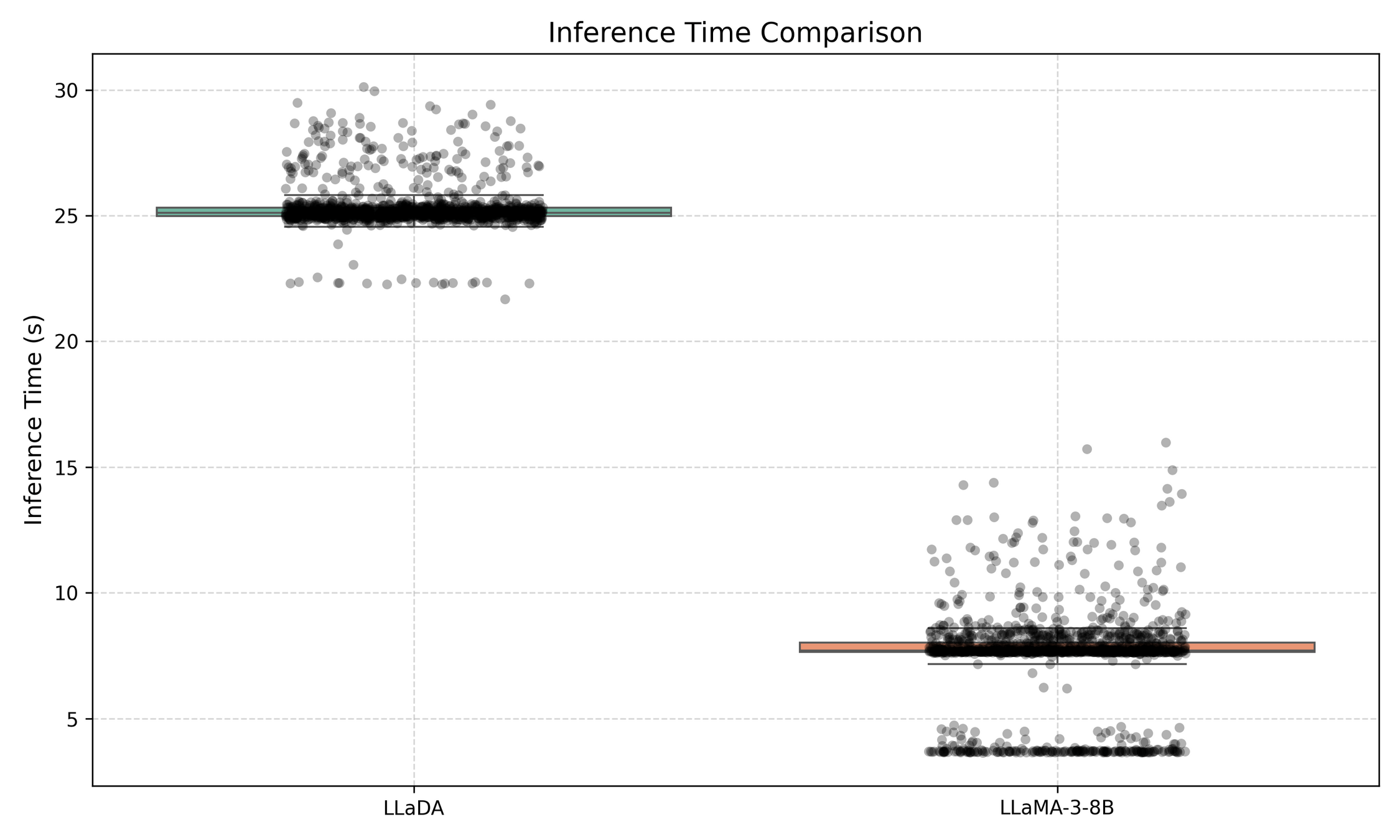
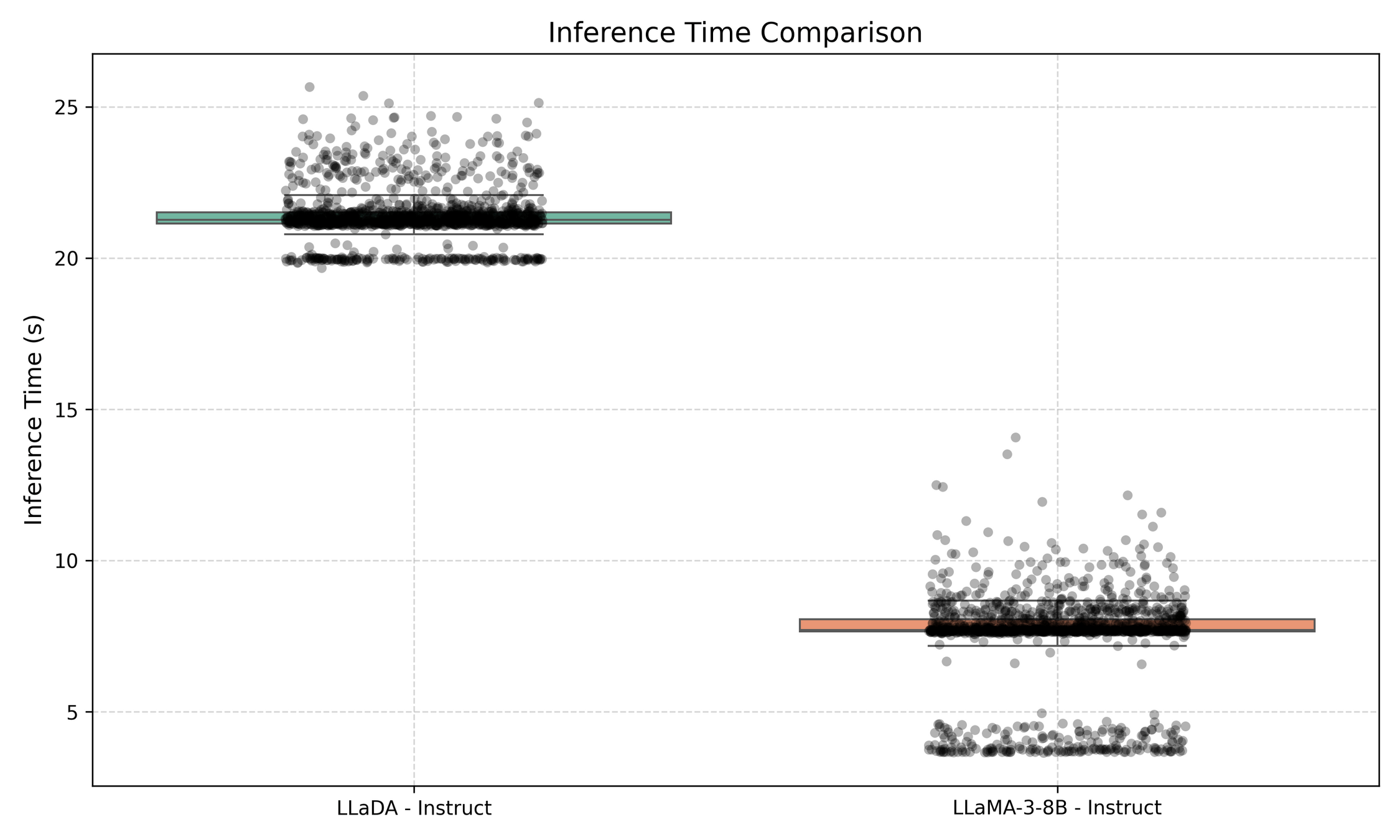
LLaDA Acc: 50.19%, LLaMA: 41.09% (GSM8k)
LLaDA Acc: 75.21%, LLaMA: 71.42% (GSM8k)

Problem Statement
- Diffusion models are powerful generative models that learn to denoise Gaussian noise into image samples.
- However, training is inefficient, especially in few-step settings like Consistency Models or DDIM.
Motivation
Accelerate Diffusion Training

Key Insight
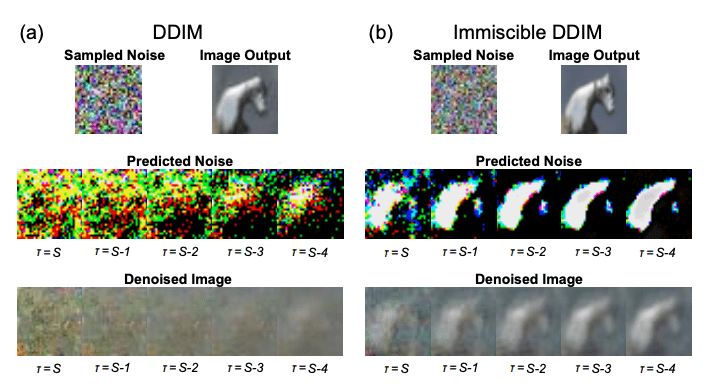
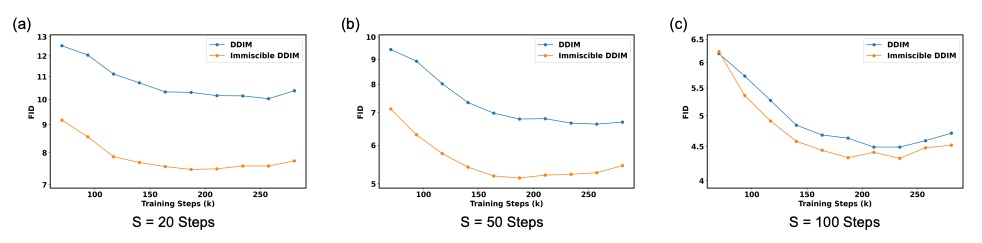
- The random pairing of images and noise (miscibility) leads to uninformative gradients and optimization difficulty.
- Goal: Improve training by structuring image-noise mapping using Immiscible Diffusion.

Posterior Under Miscibility:
Weak learning signal.

Noise Prediction in Vanilla DDIM:
where:

Immiscible Diffusion
Use linear assignment to optimally match each image in the batch with a noise sample:
- This ensures each image gets closer noise.
- Prevents global mixing.
- Implemented in 1 line using Hungarian algorithm (scipy)

Conditional Distribution After Assignment
\( f(\cdot) \): Decaying function (e.g., Gaussian)
Each image diffuses to a local region in noise space

Posterior Becomes Informative
The posterior is no longer uniform, it's peaked around assigned images.

Noise Prediction in Immiscible Diffusion
Model now learns to predict noise that corresponds to a local cluster of images.
Enables strong gradients even at high noise levels.

Batch Assignment Algorithm
Inputs:
- \( x_b \): batch of images
- \( \epsilon_b \): batch of noise
- \( t_b \): batch of diffusion steps
Output:

Contributions
- Identified miscibility issue in noise-image mapping.
- Proposed immiscible diffusion using optimal assignment.
- Theoretically derived effects via posterior + expected noise.
- Demonstrated 1-line code fix with broad applicability.
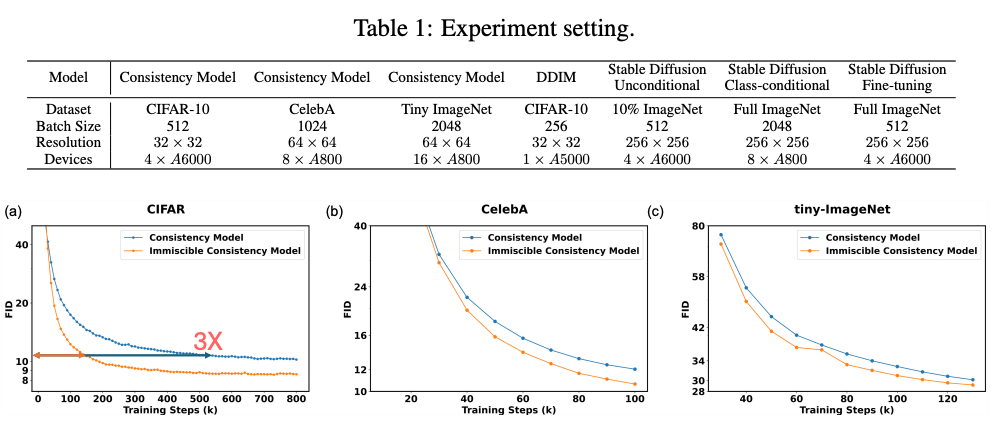
- Achieved up to 3× speedup without compromising quality






Motivation
-
Transformers: \( O(N^2) \) compute, autoregressive inference.
-
RNNs: constant-time inference but poor trainability
-
Goal: combine the best of both.
-
State Space Models (SSMs) + fast scan + physics-inspired dynamics = efficient LLMs

Motivation
-
Transformers: \( O(N^2) \) compute, autoregressive inference.
-
RNNs: constant-time inference but poor trainability
-
Goal: combine the best of both.
-
State Space Models (SSMs) + fast scan + physics-inspired dynamics = efficient LLMs

Sequence Modeling
- Input: \( x_1, \dots, x_T \)
- Output: \( y_1, \dots, y_T \)
- Continuous signals: \( x(t) \rightarrow y(t) \)
- Discrete signals: NLP, genomics, etc.

Ideal Properties
-
\( O(1) \) inference.
-
\( O(N) \) training with parallelism
-
Linearly scalable with sequence length

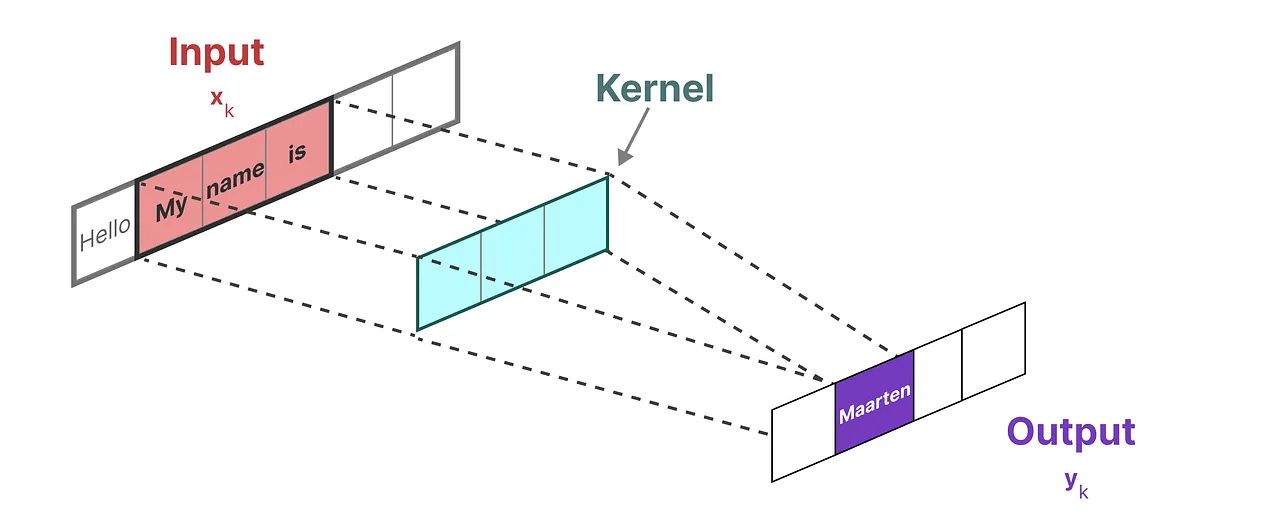
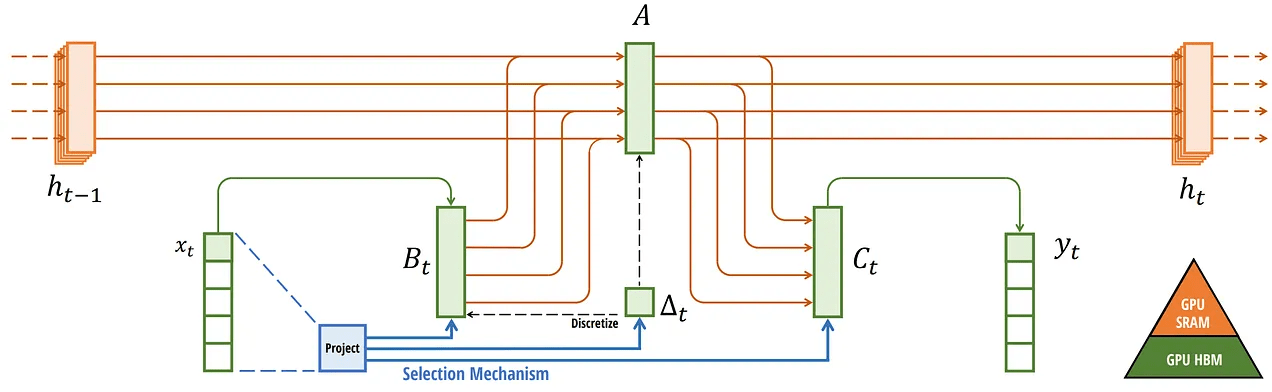
Linear State-Space Models (SSMs)


Discretization via Euler / ZOH
Takeaway: Converts continuous dynamics to discrete steps

Recurrent Update
Efficient \( O(1) \) inference

Convolutional Reformulation
Training can be parallelized as convolution

Mamba


Oscillatory State Space Models (LinOSS)
Based on forced harmonic oscillators:
Introduce auxiliary state: \( z = y' \)
Takeaway: Introduces second-order dynamics to capture oscillations

Implicit Discretization of LinOSS
Introduce auxiliary state: \( z = y' \)
Takeaway: Introduces second-order dynamics to capture oscillations

LinOSS
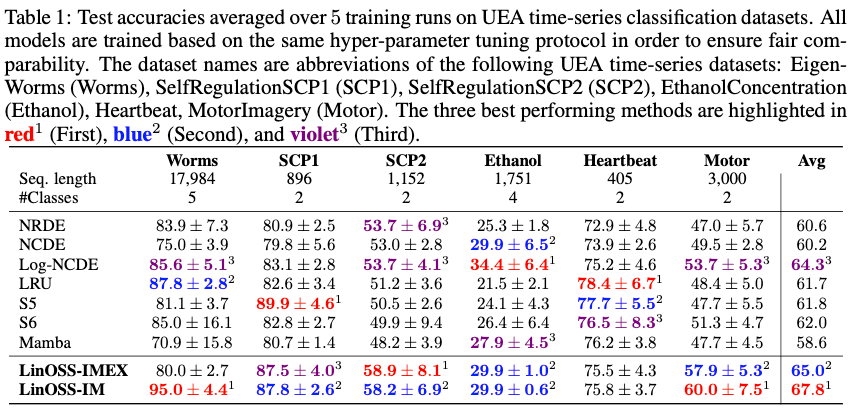

LinOSS - Why do the results matter?
- Fast Prefix-sum scan: \( O(log N) \) depth.
- Works well on GPU, supports backprop.
- Linear memory scaling with sequence length.
- No attention matrix ⇒ ideal for long-range processing
LinOSS is a enables long-sequence modeling at scale.

Future Research on Large Language Diffusion Models
- Towards efficient inference in LLaDA models.
- Existing methods such as personalization in Diffusion Models to Large Language Diffusion Models.
- User-specific adaptation
- Domain-specific knowledge
- Task tuning: Improve performance on summarization, question-answering, etc., in narrow settings.
- Memory/Contextual grounding: Make the model “remember” previous interactions or documents.
Personalization:

References:
- https://github.com/ML-GSAI/LLaDA
- https://github.com/Gen-Verse/MMaDA
- https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-mamba-and-state
- https://github.com/hkproj/mamba-notes
- https://github.com/yhli123/Immiscible-Diffusion
- https://arxiv.org/abs/2410.03943