Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A graph \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Definition.
A tree is a connected graph with no cycles.
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Lemma. If \(T=(V, E)\) is a tree and \(v\) is a leaf of the tree, then
there exists a maximum-size independent set that contains \(v\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).
Definition.
A subset \(S \subseteq V\) is called an independent set if
for all \(u,v \in S\), \({\color{IndianRed}(u,v) \notin E}\).
Lemma. If \(T=(V, E)\) is a tree and \(v\) is a leaf of the tree, then
there exists a maximum-size independent set that contains \(v\).
Maximum Independent Set
Input: A tree \(G = (V,E)\), and a positive integer \(k\).
Task: Determine if \(G\) has an independent set of size at least \(k\).

A Greedy Algorithm:
(source: Algorithm Design · Jon Kleinberg and Éva Tardos)
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Subproblems: DP[\(r\)] = solution size for subtree rooted at \(r\).
Solution: DP[root(T)]
Base Case: DP[\(v\)] = \(w(v)\) for all leaves \(v\).
How do you combine subproblems?
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Among all independent sets of \(H\) that contain the root, record the weight of the largest.
Among all independent sets of \(H\) that omit the root, record the weight of the largest.
Each independent set in \(H\) either contains the root, or omits it.
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).
...
Maximum Weight Independent Set
Input: A tree \(G = (V,E)\), a weight function \({\color{IndianRed}w: V \rightarrow \mathbb{Q}^{\geqslant 0}}\) and \(k \in \mathbb{Z}^+\).
Task: Determine if \(G\) has an independent set of weight at least \(k\).

Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
To solve Maximum-Weight Independent Set on a tree,
we took advantage of a special property of (rooted) trees:
Once we decide whether or not to include a node \(u\) in the independent set, the subproblems in each subtree become completely separated;
we can solve each as though the others did not exist.
In general graphs there might not be
a node that breaks the communication between subproblems
in the rest of the graph.
For the Independent Set Problem in general graphs,
decisions we make in one place seem to have complex repercussions all across the graph.
For how general a class of graphs can we use this notion of
limited interaction
(recursively chopping up the input using small sets of nodes)
to design efficient algorithms for a problem like
Maximum-Weight Independent Set?
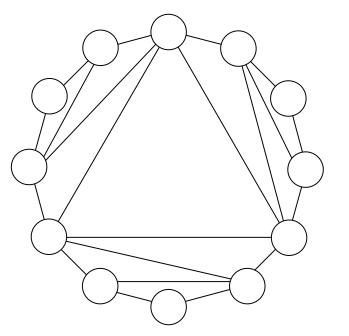
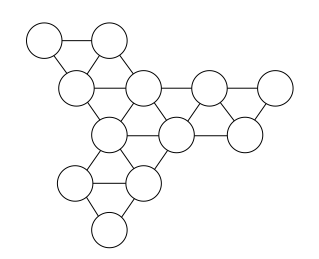
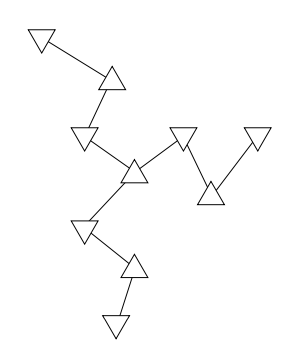


















Tree Decomposition
Formally, a tree decomposition of \(G=(V, E)\) consists of a tree \(T\) (on a different node set from \(G\) ),
and a subset \(V_t \subseteq V\) associated with each node \(t\) of \(T\).
We will call these subsets \(V_t\) the pieces or bags of the tree decomposition.
This is denoted as the ordered pair \(\left(T,\left\{V_t: t \in T\right\}\right)\).
Tree Decomposition
The tree \(T\) and the collection of pieces \(\left\{V_t: t \in T\right\}\) must satisfy the following:
(Node Coverage) Every node of \(G\) belongs to at least one piece \(V_t\).
(Edge Coverage) For every edge \(e\) of \(G\),
there is some piece \(V_t\) containing both ends of \(e\).
(Coherence) Let \(t_1, t_2\), and \(t_3\) be three nodes of \(T\) such that
\(t_2\) lies on the path from \(t_1\) to \(t_3\).
Then, if a node \(v\) of \(G\) belongs to both \(V_{t_1}\) and \(V_{t_3}\),
it also belongs to \(V_{t_2}\).
Tree Decomposition
What does a tree decomposition of a tree look like?
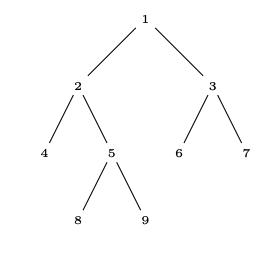
If we delete an edge \(e\) from a tree,
it falls apart into exactly two connected components.
If we delete a node \(t\) from a tree,
the tree falls apart into a number of components equal to the degree of \(t\).
Useful Separation Properties of Trees
The Coherence Property is designed to guarantee that separations of \(T\),
of both these types, correspond naturally to separations of \(G\) as well.
If \(T^{\prime}\) is a subgraph of \(T\),
we use \(G_{T^{\prime}}\) to denote the subgraph of \(G\) induced by the nodes in all pieces associated with nodes of \(T^{\prime}\),
that is, the set \(\cup_{t \in T^{\prime}} V_t\).
Separations in Tree Decompositions
Lemma. Suppose that \(T-t\) has components \(T_1, \ldots, T_d\).
Then the subgraphs
\(G_{T_1}-V_t, G_{T_2}-V_t, \ldots, G_{T_d}-V_t\)
have no nodes in common, and there are no edges between them.
Goal 1. The subgraphs \(G_{T_i}-V_t\) do not share any nodes.
Any such node \(v\) would need to belong to both
\(G_{T_i}-V_t\) and \(G_{T_j}-V_t\) for some \(i \neq j\).
Such a node \(v\) belongs
to some piece \(V_x\) with \(x \in T_i\), and
to some piece \(V_y\) with \(y \in T_j\).
Since \(t\) lies on the \(x-y\) path in \(T\),
it follows from the Coherence Property that \(v\) lies in \(V_t\).
So \(v\) belongs to neither \(G_{T_i}-V_t\) nor \(G_{T_j}-V_t\).
Goal 2. There is no edge \((u,v)\) with \(u \in G_{T_i} - V_t\) and \(v \in G_{T_j} - V_t\),
for some \(j \neq i\).
There has to be some piece \(V_x\) containing both \(u\) and \(v\).
Suppose \(x \notin T_i\).
Then the node \(u\) belongs to both \(V_x\) and \(V_y\).
Recall: \(u \in G_{T_i} - V_t\).
...so \(u\) must be in a set \(V_y\) for some \(y\) in \(T_i\).
Since \(t\) lies on the \(x-y\) path in \(T\), it follows that \(u\) also belongs to \(V_t\).
Therefore \(u\) does not lie in \(G_{T_i}-V_t\), a contradiction.
(The other case is symmetric.)
If \(T^{\prime}\) is a subgraph of \(T\),
we use \(G_{T^{\prime}}\) to denote the subgraph of \(G\) induced by the nodes in all pieces associated with nodes of \(T^{\prime}\),
that is, the set \(\cup_{t \in T^{\prime}} V_t\).
Separations in Tree Decompositions
Lemma. Let \(X\) and \(Y\) be the two components of \(T\)
after the deletion of the edge \((x, y)\).
Then deleting the set \(V_x \cap V_y\) from \(V\) disconnects \(G\) into the two subgraphs \(G_X-\left(V_x \cap V_y\right)\) and \(G_Y-\left(V_x \cap V_y\right)\)
More precisely, these two subgraphs do not share any nodes, and there is no edge with one end in each of them.
\(G_X-V_x \cap V_y\)
\(G_Y-V_x \cap V_y\)
\(V_x\)
\(V_y\)
Treewidth
Note: every graph has a tree decomposition.
(One bag and all vertices.)
Q. What tree decompositions are useful?
When the separations are small.
We define the width of a tree decomposition \(\left(T,\left\{V_t\right\}\right)\) to be one less than the maximum size of any piece \(V_t\):
\({\color{IndianRed}\text { width }\left(T,\left\{V_t\right\}\right)=\max _t\left|V_t\right|-1.}\)
We then define the tree-width of \(G\) to be the minimum width of any tree decomposition of \(G\).
Treewidth
Lemma. A connected graph \(G\) has tree-width 1
if and only if it is a tree.
Treewidth
Non-redundancy.
Treewidth
Non-redundancy.
Treewidth
Non-redundancy.
Treewidth
Can always ensure that there is no edge \((x, y)\) of the underlying tree such that \(V_x \subseteq V_y\).
Treewidth
Can always ensure that there is no edge \((x, y)\) of the underlying tree such that \(V_x \subseteq V_y\).
Lemma. Any nonredundant tree decomposition of an \(n\)-node graph has at most \(n\) pieces.
Treewidth
How do we determine the treewidth of a graph?
NP-complete to check if a graph has treewidth at most \(w\).
Lemma. Given a graph \(G\) and a parameter \(w\), there is an algorithm that does one of the following two things:
- it produces a tree decomposition of width less than \({\color{SeaGreen}4w}\), or
- it reports (correctly) that \(G\) does not have tree-width less than \(w\).
The running time of the algorithm is \(O(f(w) \cdot m n)\),
for a function \(f(\cdot)\) that depends only on \(w\).
Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
Input. A graph \(G = (V,E)\), a weight function \(w: V \rightarrow \mathbb{Q}^{\geqslant 0}\), and a tree decomposition \(T;\{V_t\}\) of width \(w\).
Task. Find a maximum-weight independent subset of \(G\).
Root the tree \(T\) at a node \(r\).
For any node \(t\), let \(T_t\) denote the subtree rooted at \(t\).
Recall that \(G_{T_t}\) denotes the subgraph of \(G\) induced by the nodes in all pieces associated with nodes of \(T_t\).
For a subset \(U\) of \(V\), \(w(U)=\sum_{u \in U} w_u\).
For notational simplicity, we will also write this subgraph as \(G_t\).
Input. A graph \(G = (V,E)\), a weight function \(w: V \rightarrow \mathbb{Q}^{\geqslant 0}\), and a tree decomposition \(T;\{V_t\}\) of width \(w\).
Task. Find a maximum-weight independent subset of \(G\).
We define a set of subproblems for each subtree \(T_t\), one corresponding to each possible subset \(U\) of \(V_t\) that may represent the intersection of the optimal solution with \(V_t\).
\(V_t\)
For each independent set \(U \subseteq V_t\), we write \(f_t(U)\) to denote the maximum weight of an independent set \(S\) in \(G_t\), subject to the requirement that \(S \cap V_t=U\).
Input. A graph \(G = (V,E)\), a weight function \(w: V \rightarrow \mathbb{Q}^{\geqslant 0}\), and a tree decomposition \(T;\{V_t\}\) of width \(w\).
Task. Find a maximum-weight independent subset of \(G\).
We define a set of subproblems for each subtree \(T_t\), one corresponding to each possible subset \(U\) of \(V_t\) that may represent the intersection of the optimal solution with \(V_t\).
\(V_t\)
\(2^w\) subproblems associated with each node.
Final answer: take the best solution among all subsets of the root.
\(V_t\)
\(G_t\)
\(V_t\)
\(G_{t_1}\)
\(G_{t_k}\)
\(V_{t_1}\)
\(V_{t_k}\)
\(\ldots\)
\(\ldots\)
The value of \(f_t(U)\) is given by the following recurrence:
\(\begin{aligned}f_t(U)= & w(U)+\sum_{i=1}^d \max \left\{f_{t_i}\left(U_i\right)-w\left(U_i \cap U\right):\right. \\& \left.U_i \cap V_t=U \cap V_{t_i} \text { and } U_i \subseteq V_{t_i} \text { is independent }\right\}.\end{aligned}\)
The Recurrence
The value of \(f_t(U)\) is given by the following recurrence:
\(\begin{aligned}f_t(U)= & w(U)+\sum_{i=1}^d \max \left\{f_{t_i}\left(U_i\right)-w\left(U_i \cap U\right):\right. \\& \left.U_i \cap V_t=U \cap V_{t_i} \text { and } {\color{IndianRed}U_i \subseteq V_{t_i}} \text { is independent }\right\}.\end{aligned}\)
The Recurrence
The value of \(f_t(U)\) is given by the following recurrence:
\(\begin{aligned}f_t(U)= & w(U)+\sum_{i=1}^d \max \left\{f_{t_i}\left(U_i\right)-w\left(U_i \cap U\right):\right. \\& \left.{\color{SeaGreen}U_i \cap V_t=U \cap V_{t_i}} \text { and } U_i \subseteq V_{t_i} \text { is independent }\right\}.\end{aligned}\)
The Recurrence
The value of \(f_t(U)\) is given by the following recurrence:
\(\begin{aligned}f_t(U)= & w(U)+\sum_{i=1}^d \max \left\{f_{t_i}\left(U_i\right){\color{DodgerBlue} - w\left(U_i \cap U\right)}:\right. \\& \left.U_i \cap V_t=U \cap V_{t_i} \text { and } U_i \subseteq V_{t_i} \text { is independent }\right\}.\end{aligned}\)
The Recurrence
For a leaf \(t\),
\(f_t(U)\) is given by \(w(U)\)
if \(U\) is an independent subset of \(V_t\),
and is not defined otherwise.
Base Cases
Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
Nice Tree Decompositions
All leaves are empty.
Every node is either
an introduce vertex node, an introduce edge node,
a forget node, or a join node.
Nice Tree Decompositions
All leaves are empty.
Every node is either
an introduce vertex node, an introduce edge node,
a forget node, or a join node.
\(X_{t^\prime}\)
\(X_t := X_{t^\prime} \cup \{v\} \)
Nice Tree Decompositions
All leaves are empty.
Every node is either
an introduce vertex node, an introduce edge node,
a forget node, or a join node.
\(X_{t^\prime}\)
\(X_t := X_{t^\prime} \setminus \{v\} \)
Nice Tree Decompositions
All leaves are empty.
Every node is either
an introduce vertex node, an introduce edge node,
a forget node, or a join node.
\(X_p \)
\(X_q \)
\(X_t = X_p = X_q \)
Nice Tree Decompositions
All leaves are empty.
Every node is either
an introduce vertex node, an introduce edge node,
a forget node, or a join node.
From tree decompositions to graphs
\(G_t=\left(V_t, E_t=\{e: e\right.\) is introduced in the subtree rooted at \(\left.t\}\right)\).
\(V_t := \cup_{t^\prime \text{ child of } t} V_{t^\prime}\).
Treewidth DP for minimum dominating set
A set of vertices \(D\) is a dominating set in graph \(G\) if \(V(G)=N[D]\).
The goal is to provide a dynamic-programming algorithm on a tree decomposition that determines the minimum possible size of a dominating set of the input graph \(G\).
Treewidth DP for minimum dominating set
A set of vertices \(D\) is a dominating set in graph \(G\) if \(V(G)=N[D]\).
The goal is to provide a dynamic-programming algorithm on a tree decomposition that determines the minimum possible size of a dominating set of the input graph \(G\).
Note: the complement of any maximal independent set
is a dominating set.
A coloring of bag \(X_t\) is a mapping
\(f: X_t \rightarrow\{0, \hat{0}, 1\}\)
assigning three different colors to vertices of the bag.
Black, represented by 1 .
The meaning is that all black vertices have to be contained in the partial solution in \(G_t\).
White, represented by 0 .
The meaning is that all white vertices are not contained in the partial solution and must be dominated by it.
Grey, represented by \(\hat{0}\).
The meaning is that all grey vertices are not contained in the partial solution, but do not have to be dominated by it.
For a node \(t\), there are \(3^{\left|X_t\right|}\) colorings of \(X_t\);
these colorings form the space of states at node \(t\).
For a coloring \(f\) of \(X_t\), we denote by \(c[t, f]\) the minimum size of a set \(D \subseteq V_t\) such that:
(a) \(D \cap X_t=f^{-1}(1)\), which is the set of vertices of \(X_t\) colored black.
(b) Every vertex of \(V_t \backslash f^{-1}(\hat{0})\) either is in \(D\) or is adjacent in \(G_t\) to a vertex of \(D\). That is, \(D\) dominates all vertices of \(V_t\) in graph \(G_t\), except possibly some grey vertices in \(X_t\).
Introduce Node
\(X_{t^\prime}\)
\(X_t := X_{t^\prime} \cup \{v\} \)
\(c[t, f]= \begin{cases}+\infty & \text { when } f(v)=0 \\ c\left[t^{\prime},\left.f\right|_{X_{t^{\prime}}}\right] & \text { when } f(v)=\hat{0} \\ 1+c\left[t^{\prime},\left.f\right|_{X_{t^{\prime}}}\right] & \text { when } f(v)=1\end{cases}\)
Introduce Edge Node
\(c[t, f]= \begin{cases}c\left[t^{\prime}, f_{v \rightarrow 0}\right] & \text { when }(f(u), f(v))=(1,0), \\ c\left[t^{\prime}, f_{u \rightarrow 0}\right] & \text { when }(f(u), f(v))=(0,1), \\ c\left[t^{\prime}, f\right] & \text { otherwise. }\end{cases}\)
Forget Node
\(X_{t^\prime}\)
\(X_t := X_{t^\prime} \setminus \{v\} \)
\(c[t, f]=\min \left\{c\left[t^{\prime}, f_{w \rightarrow 1}\right], c\left[t^{\prime}, f_{w \rightarrow 0}\right]\right\}\).
Join Node
\(X_p \)
\(X_q \)
\(X_t = X_p = X_q \)
\(c[t, f]=\min _{f_1, f_2}\left\{c\left[t_1, f_1\right]+c\left[t_2, f_2\right]-\left|f^{-1}(1)\right|\right\}\)
Advanced Algorithms
Part 3. DP over trees and beyond
Part 1a. DP over Paths and Trees
Part 1b. Treewidth: Definition and Computation
Part 1c. MWIS over Bounded Treewidth
Part 1d. Dominating Set over Bounded Treewidth
Part 1e. Treewidth and monadic second-order logic
\(\begin{aligned} \operatorname{conn}(X)= & \forall_{Y \subseteq V}\left[\left(\exists_{u \in X} u \in Y \wedge \exists_{v \in X} v \notin Y\right)\right. \\ & \\ & \left.\Rightarrow\left(\exists_{e \in E} \exists_{u \in X} \exists_{v \in X} \operatorname{inc}(u, e) \wedge \operatorname{inc}(v, e) \wedge u \in Y \wedge v \notin Y\right)\right] .\end{aligned}\)