Advanced Algorithms
Intractability I. NP-completeness
Part 1a. Overall Framework
Part 1b. Reductions from Partition & Variants
Part 1c. Reductions from SAT
Part 1d. Hardness of Yin-Yang Puzzles
Part 1e. Using ILP - II
Advanced Algorithms
Part 4. Solving Problems by Transformations
Part 1a. Using Flows - I
Part 1b. Using Flows - II
Part 1c. Using SAT
Part 1d. Using ILP - I
Part 1e. Using ILP - II
Part 1a. Using Flows - I
Advanced Algorithms
Part 4. Solving Problems by Transformations
Part 1a. Using Flows - I
Part 1b. Using Flows - II
Part 1c. Using SAT
Part 1d. Using ILP - I
Part 1e. Using ILP - II
Part 1a. Using Flows - I
Advanced Algorithms
Part 4. Solving Problems by Transformations
Part 1a. Using Flows - I
Part 1b. Using Flows - II
Part 1c. Using SAT
Part 1d. Using ILP - I
Part 1e. Using ILP - II
Part 1a. Using Flows - I
For any \(C>\) 0 in any infinite \(\pm 1\) sequence \(\left(x_n\right)\)
there exists a subsequence \(x_d, x_{2 d}, x_{3 d}, \ldots, x_{k d}\),
for some positive integers \(k\) and \(d\),
such that \(\left|\sum_{i=1}^k x_{i d}\right|>C\).
Erdős Discrepancy Conjecture
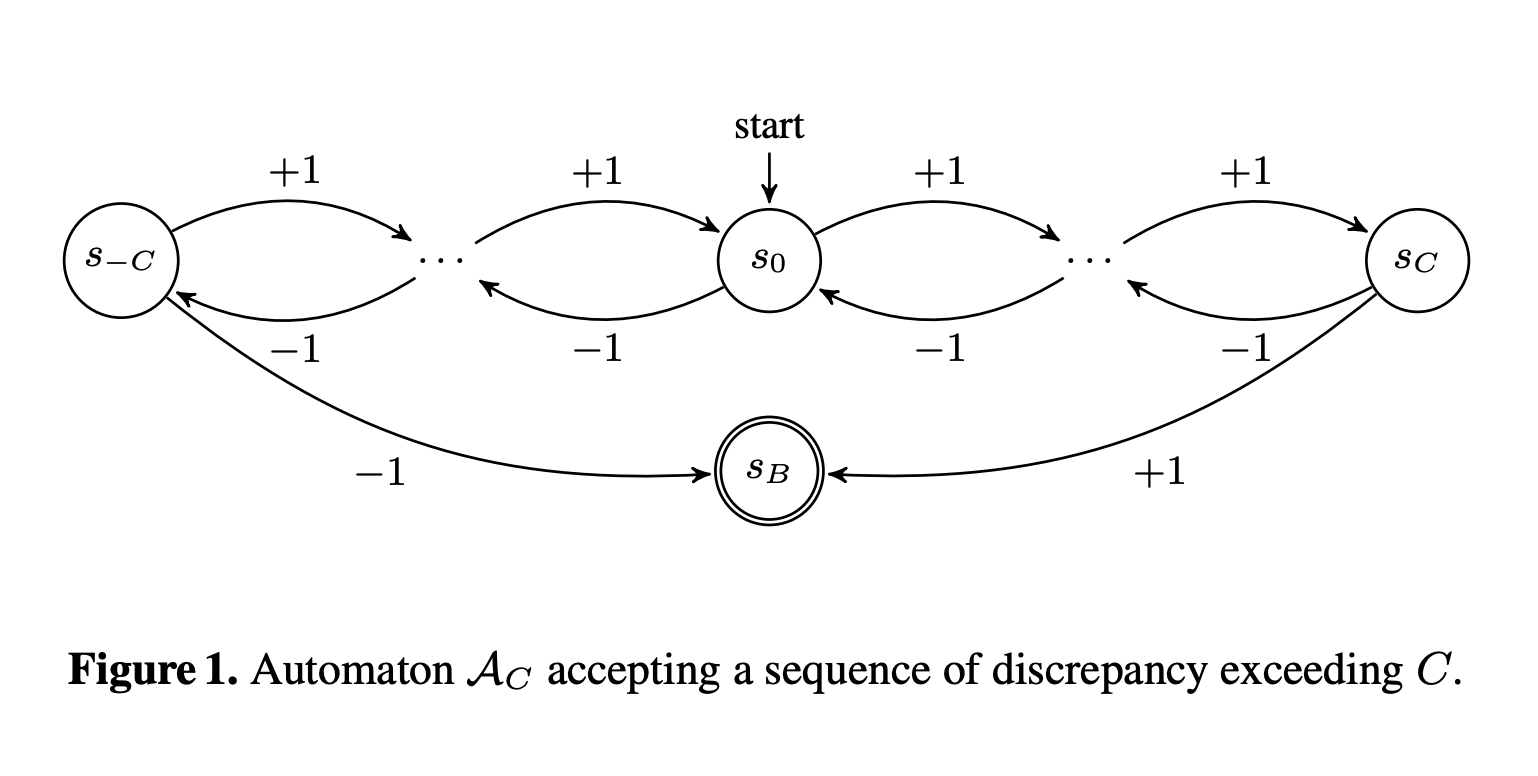
\(\begin{aligned} \phi_{(l, C, d)}=s_0^{(1, d)} \bigwedge_{i=1}^{\left\lfloor\frac{l}{d}\right\rfloor}[ & \bigwedge_{-C \leq j<C}\left(s_j^{(i, d)} \wedge p_{i d} \rightarrow s_{j+1}^{(i+1, d)}\right) \wedge \\ & \bigwedge_{-C<j \leq C}\left(s_j^{(i, d)} \wedge \neg p_{i d} \rightarrow s_{j-1}^{(i+1, d)}\right) \wedge \\ & \left(s_C^{(i, d)} \wedge p_{i d} \rightarrow B\right) \wedge \\ & \left.\left(s_{-C}^{(i, d)} \wedge \neg p_{i d} \rightarrow B\right)\right]\end{aligned}\)
\(\phi_{(l, C)}=\neg B \wedge \bigwedge_{d=1}^{\left\lfloor\frac{l}{C+1}\right\rfloor} \phi_{(l, C, d)} \wedge\) frame \(_{(l, C)}\),
where frame \((l, C)\) is a Boolean formula encoding that the automaton state is correctly defined,
that is,
exactly one proposition from each of the sets \(\left\{s_j^{(i, d)} \mid-C \leq j \leq C\right\}\), for \(d=1, \ldots,\left\lfloor\frac{l}{C+1}\right\rfloor\) and \(1 \leq i \leq\left\lfloor\frac{l}{d}\right\rfloor\), is true in every model of \(\phi_{(l, C)}\).
The formula \(\phi_{(l, C)}\) is satisfiable if, and only if, there exists \(a \pm 1\) sequence \(\bar{x}=x_1, \ldots, x_l\) of length \(l\) of discrepancy \(C\).
Moreover, if \(\phi_{(l, C)}\) is satisfiable, the sequence \(\bar{x}=x_1, \ldots, x_l\) of discrepancy \(C\) is uniquely identified by the assignment of truth values to propositions \(p_1, \ldots p_l\).
Advanced Algorithms
Part 4. Solving Problems by Transformations
Part 1a. Using Flows - I
Part 1b. Using Flows - II
Part 1c. Using SAT
Part 1d. Using ILP - I
Part 1e. Using ILP - II
Part 1a. Using Flows - I
Advanced Algorithms
Part 4. Solving Problems by Transformations
Part 1a. Using Flows - I
Part 1b. Using Flows - II
Part 1c. Using SAT
Part 1d. Using ILP - I
Part 1e. Using ILP - II
Part 1a. Using Flows - I