CALDAM
Indo-Dutch
Pre-Conference School on Algorithms and Combinatorics
Games on Graphs & Eternal Vertex Cover
Neeldhara Misra

OUTLINE
OUTLINE
OUTLINE
Pursuit-Evasion Games
Two players: cop(s) and robber(s)
Typically both players move at the same speed along edges.
Turn-based strategy game with perfect information.
In the first move, the cops are positioned at some vertices of the graph.
The robber wins if they can evade capture forever.
In the second move, the robber picks their spot.
Otherwise, the cops win.
Pursuit-Evasion Games
A graph is called a cop-win
if one cop is enough to corner the robber.
How can we determine if a graph is a cop-win?
A Pitfall ⚠️
For an edge \((u,v)\), \(u\) is a pitfall with an attack from \(v\) if \(N(u) \subseteq N(v)\).
\(v\)
\(u\)
If a graph is a robber-win,
then perhaps we need more cops?
The cop number of a graph is the smallest number of cops you need to deploy for the cops to win.
If a graph is a robber-win,
then perhaps we need more cops?
The cop number of a graph is the smallest number of cops you need to deploy for the cops to win.
Is the cop number well-defined?
Can the cop number be arbitrarily large in the #vertices?
Variations!
Drunk robbers.
Lazy cops.
Cops on helicopters.
Imperfect information.
Long-range robbers
Infinite graphs.
OUTLINE































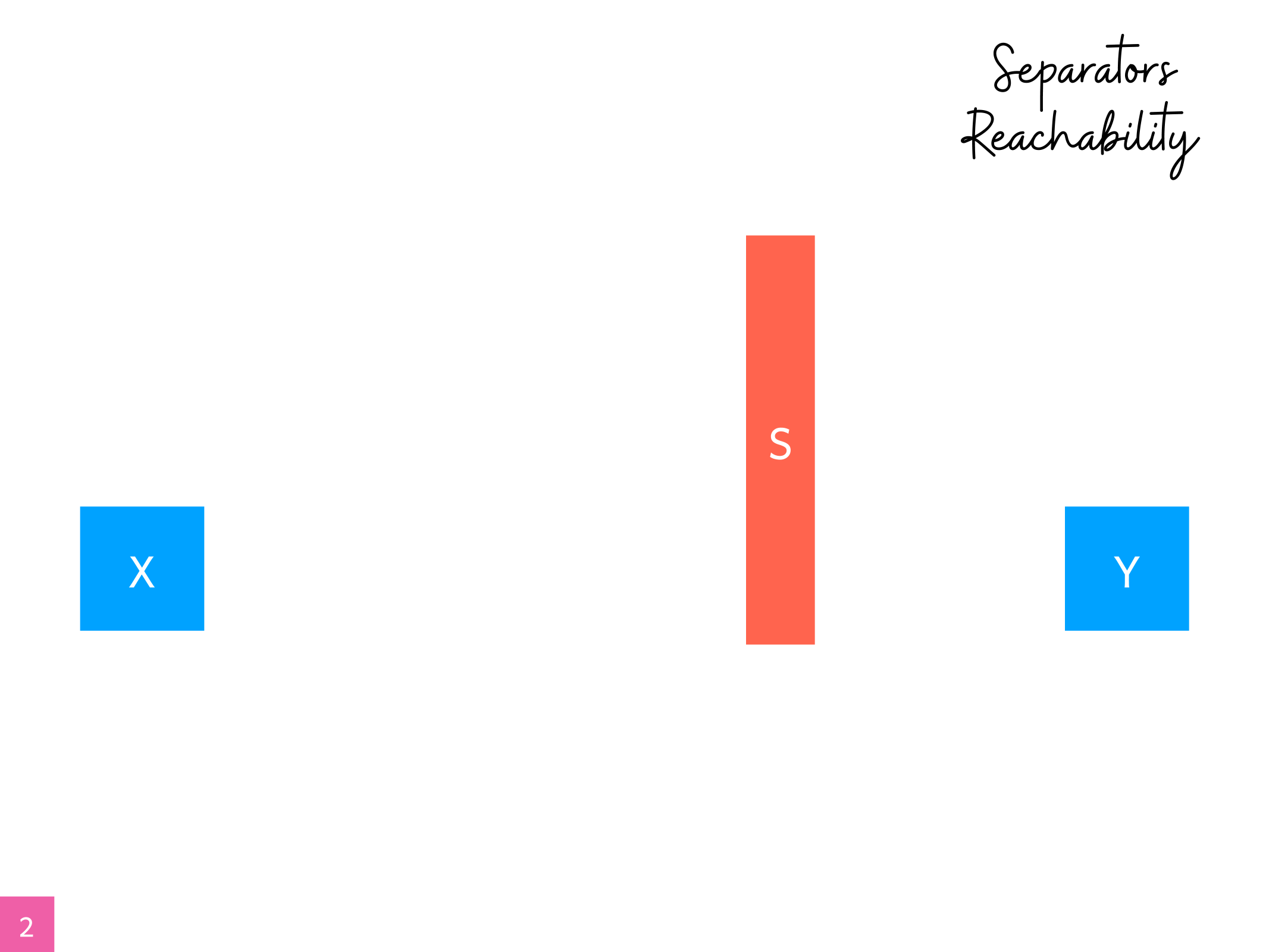












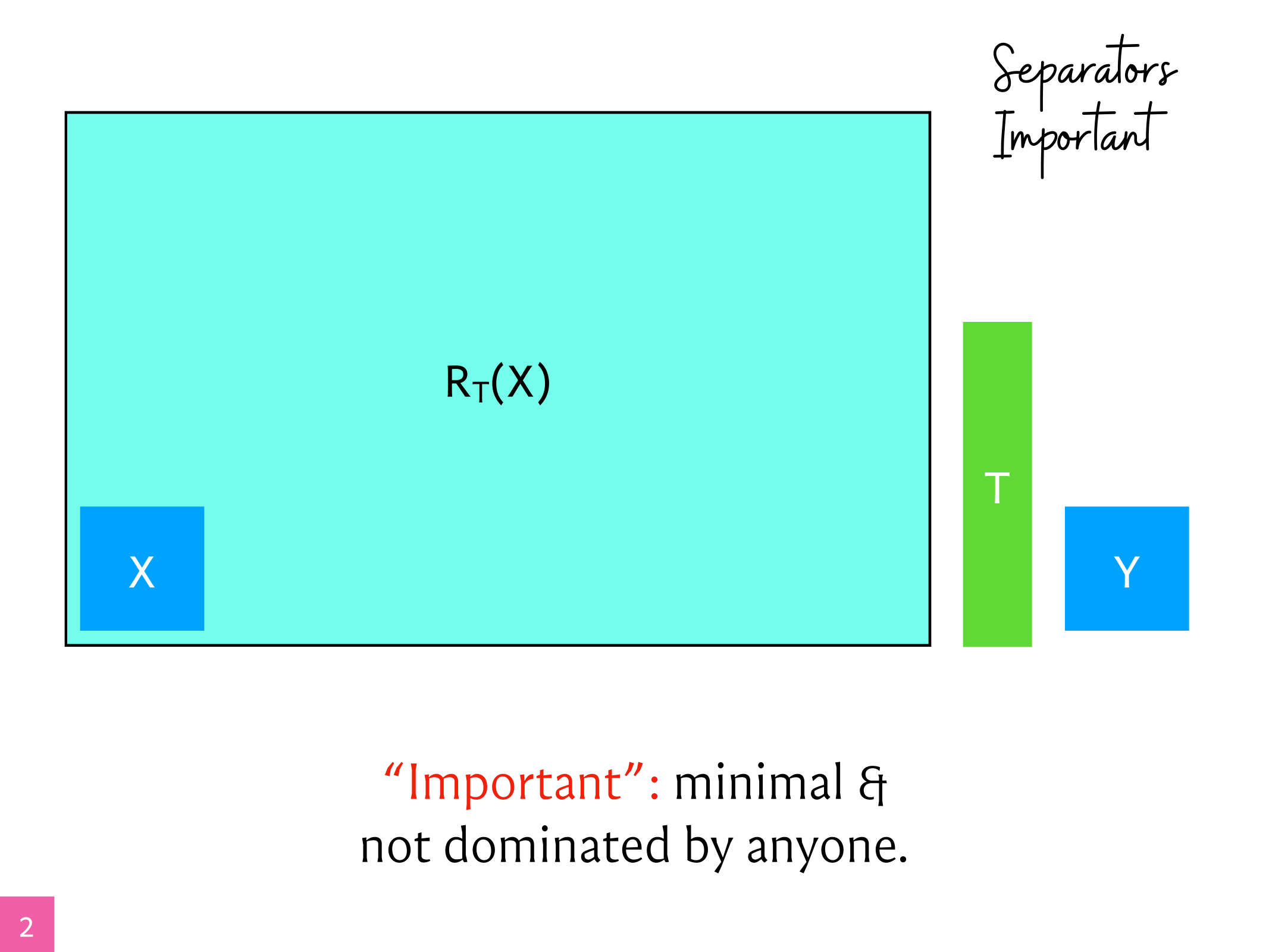

















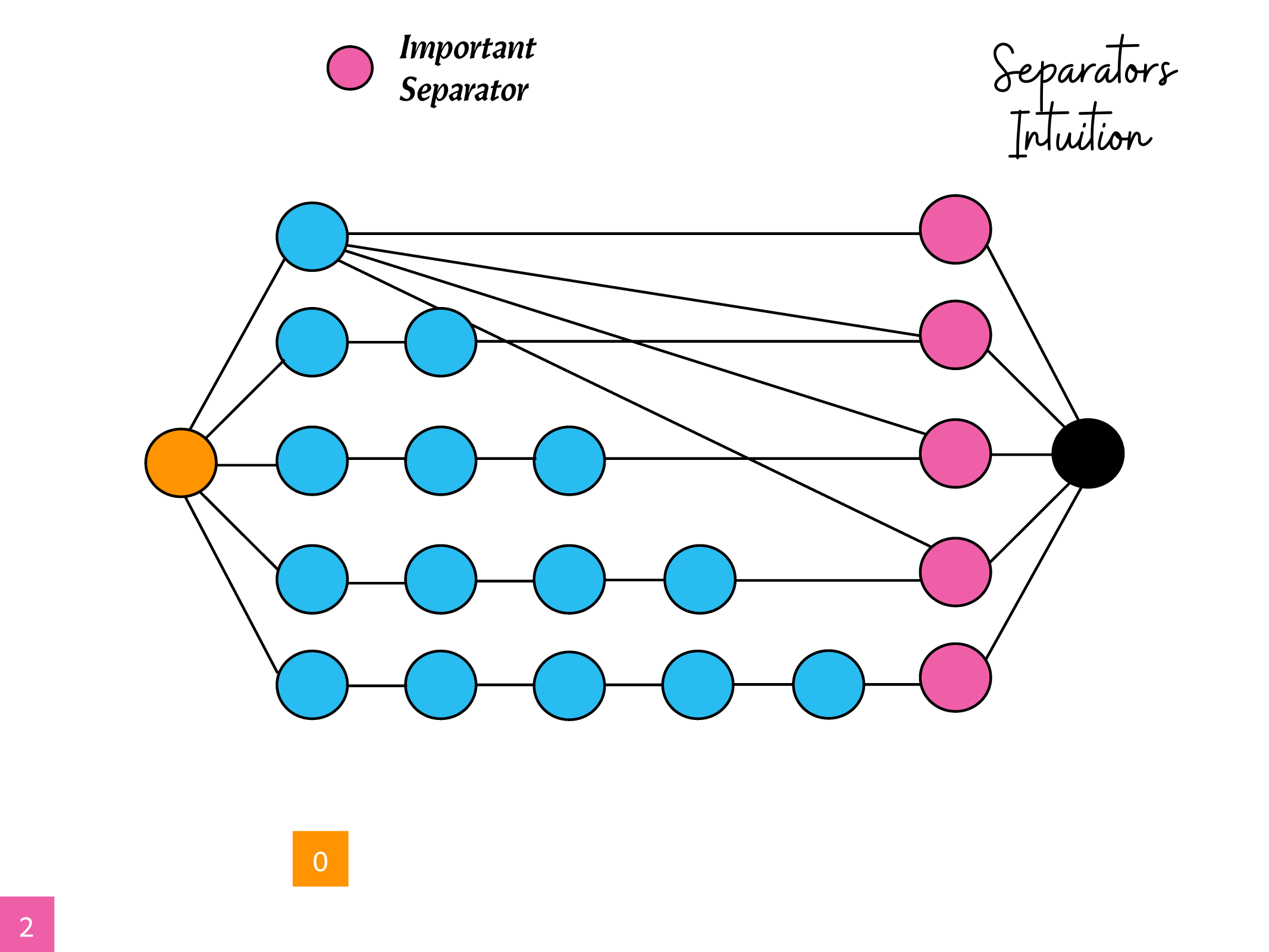






















OUTLINE
Eternal Vertex Cover
To begin with, a defender places guards on some vertices of a graph.
In every move, an attacker attacks some edge.
In response, the defender moves the guards along the edges in such a
manner that at least one guard moves along the attacked edge.
If such a movement is not possible, attacker wins.
If the defender can defend an infinite sequence of attacks, defender wins.
The minimum number of guards with which defender has a winning
strategy is called the Eternal Vertex Cover Number of the Graph G.
Initial position of the guards.
The first attack.
The first defense.
The first defense.

The first defense.

All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
All good again!
A vertex cover is a subset of vertices such that every edge has at least one endpoint in it.
In every round of the EVC game, if the attacker has not won then the guards are positioned on a vertex cover.
Finding optimal EVCs is computationally as hard as finding a vertex cover.
What we know about Eternal Vertex Cover
EVC admits a 2-approximation.
EVC is tractable when parameterized by the solution size.
MVC(G) \(\leqslant\) EVC(G) \(\leqslant\) 2 \(\cdot\) MVC(G)
Polynomial time algorithms known for a few graph classes.
On bipartite graphs: VC is easy but EVC turns out to be hard.
References

References
References
References
An Invitation
https://slides.com/neeldhara/caldam2023/
These slides:
Continue the conversation:
@neeldhara | neeldhara.com