The Math of
Cutting Cakes and Dividing Candy
Neeldhara Misra
IIT Gandhinagar
DAIICT · 23rd October 2024
Math models are useful in the social sciences
Social sciences motivate
new math
Takeaways...
Source
Cake Cutting
Hesiod's Theogony:
Prometheus cuts ox in two, offers Zeus choice
Old Testament Book of Genesis:
Abraham offers Lot choice: land to left or right
Mining in the Ocean:
The United Nations Convention on the Law of the Sea applies a procedure similar to divide-and-choose for allocating areas in the ocean among countries.
Cake Cutting
Jack Sprat could eat no fat
His wife could eat no lean
So 'twixt them both they cleared the cloth,
And licked the platter clean
Mother Goose Nursery Rhyme
Cake Cutting
Outline
Outline
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over bundles of items.
Goal: Make everyone happy. 🙌
📦 →
🙋♀️
💐 →
🤦♀️
🍰 →
🤩
🚗 →
🤷♀️
Task:
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop: Agents have preferences over bundles of items.
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \pi(a_i) \cap \pi(a_j) = \emptyset $$
No sharing...
Complete
$$ \bigcup_{a \in A} \pi(a) = R $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop: Agents have preferences over bundles of items.
Goal: Make everyone happy. 🙌
Compute an allocation
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow \mathbb{Z} $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
0/1 Valuations
$$ \{0,1\} $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
Additive Valuations
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
For all subsets \( S \subseteq R \), \( \nu_\ell(S) = \sum_{o \in S} \nu_\ell(\{o\}) \).
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
If 🙋♀️ values the items 🍰 and 💐 at 1 each, then she values {🍰, 💐} at 2.
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🙌
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😀 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
👀 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😬 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😠 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: Make everyone happy. 🤔
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: The allocation \( \pi \) creates no envy
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: The allocation \( \pi \) creates no envy
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
and a knows b.
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: The allocation \( \pi \) creates no envy
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
and a knows b.
(between friends)
Fair Division
Distribute m items among n agents.
Backdrop: Agents have preferences over items.
Goal: Make everyone happy. 🙌
Task:
$$ \pi: A \rightarrow 2^R $$
Fair Division
Backdrop:
Goal: The allocation \( \pi \) creates no envy
Compute an allocation
$$ \nu_\ell: 2^R \rightarrow $$
$$ \{0,1\} $$
😭 → {🍰,🍵}
😍 → {🍔,🍟,☕️}
Agent a envies b in \( \pi \) if \( v_a(\pi(b)) > v_a(\pi(a)) \)
and a knows b.
(between friends)
and a social network on \( A \)
Fair Division via Social Comparison
AAMAS 2017
Rediet Abebe,
Jon M. Kleinberg, and David C. Parkes

Networked fairness in cake cutting
IJCAI 2017
Xiaohui Bei.
Youming Qiao, and Shengyu Zhang.

Preprint (2022)
Ganesh Ghalme, Xin Huang, Nidhi Rathi
Envy-Free Cake Cutting with Graph Constraints

Local envy-freeness in house allocation problems.
AAMAS 2018
Aurélie Beynier, Yann Chevaleyre, Laurent Gourvès, Julien Lesca, Nicolas Maudet, and Anaëlle Wilczynski.

Envy-Free Allocations Respecting Social Networks
Journal of Artifical Intelligence, 2022
&
AAMAS 2018
Robert Bredereck,
Andrzej Kaczmarczyk,
and Rolf Niedermeier.

Parameterized Complexity of Envy-Free
Resource Allocation
in Social Networks
AAAI 2020
Eduard Eiben,
Robert Ganian,
Thekla Hamm,
and Sebastian Ordyniak

Preprint (2022)
Justin Payan, Rik Sengupta, Vignesh Viswanathan

Locally EFX Allocations Over a Graph


Survey (2021)
Outline
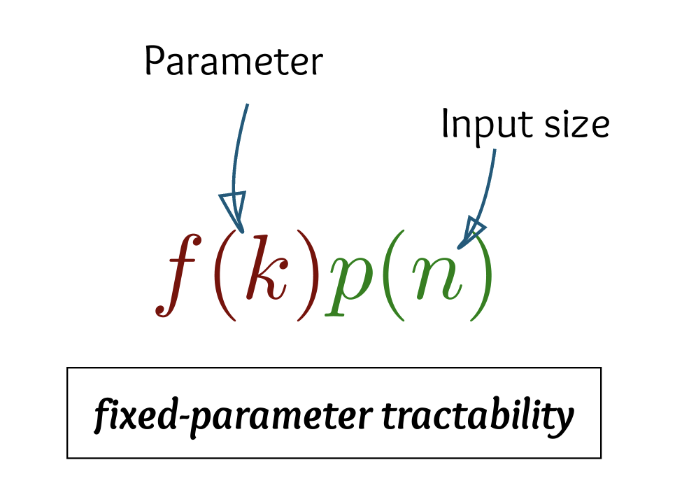
FPT Algorithm:
Solve the problem in time \(f(k)\cdot n^{O(1)}\), for some appropriate parameter \(k\).
Kernelization:
Reduce the problem in time \(n^{O(1)}\),
to an equivalent instance whose size is bounded by \(f(k)\),
for some appropriate parameter \(k\).
XP Algorithm:
Solve the problem in time \(O^\star(n^{f(k)})\), for some appropriate parameter \(k\).
FPT Algorithm:
Solve the problem in time \(f(k)\cdot n^{O(1)}\), for some appropriate parameter \(k\).
Kernelization:
Reduce the problem in time \(n^{O(1)}\),
to an equivalent instance whose size is bounded by \(f(k)\),
for some appropriate parameter \(k\).
XP Algorithm:
Solve the problem in time \(O^\star(n^{f(k)})\), for some appropriate parameter \(k\).
The art of parameterization
Useful
for real
Useful
for us
An example
Finding an efficient (PO) envy-free allocation is fixed-parameter tractable with respect to the combined parameter (n+z)
for identical monotonic additive preferences.
-
n denotes the number of agents and
-
z is the number of different values that occur in the utility functions.
\(f_j := (u_1(r_j),u_2(r_j),...,u_n(r_j)).\)
Define the signature of a resource
to be a \(n\)-tuple that collects all the utilities that agents have for said resource.
#signatures ~ \(z^n\)
\(f = (u_1( ),u_2( ), \ldots\)
\(f = (u_1( ),u_2( ), \ldots\)
Objects with the same signature are indistinguishable.
For each agent \(a_i \in A\) and each fingerprint \(f\):
\(x_f^i\) → #of resources
with fingerprint \(f\)
allocated to agent i.
\(\forall 1 \leq p \leq n, 1 \leq q \leq n:\)
\(\sum_{f \in F} x_p^f \cdot f[p] \geq \sum_{f \in F} x_{q}^f \cdot f[p]\)
Parameters for Resource Allocation
number of agents
number of items
number of agent types
number of item types
max utility
#distinct utilities
graph parameters (e.g, vertex cover, treewidth, etc.)
domain parameters (e.g, rank/sparsity/etc. of the utility matrix)
Recap: the parameterized paradigm
Parameterized complexity: acknowledge the presence of additional structure, which manifests as a secondary measurement a parameter.
Design algorithms that restrict the combinatorial explosion
to a function of the parameter.
Undirected Graphs
Goal: Determine the existence of a
complete and locally envy-free allocation.
NP-complete
AGMW'15, HSVWX'20
(even when valuations are binary
and the graph is complete).
Undirected Graphs
Goal: Determine the existence of a
complete and locally envy-free allocation.
P
even when valuations are binary and identical.*
*for connected graphs
Directed Graphs
Goal: Determine the existence of a
complete and locally envy-free allocation.
NP-hard
(even when valuations are binary and identical).
BKN'18
Undirected Graphs
Goal: Determine the existence of a
complete and locally envy-free allocation.
NP-hard
even when valuations are binary and nearly identical.
Directed Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
P
if the social network is a DAG
BKN'18
Undirected Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
NP-hard
even if the social network is a path
Undirected Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
NP-hard
even if* the social network is a star
*general utilities
EGHO'20
Undirected Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
W[1]-hard
parameterized by the vertex cover number for 0/1 utilities
Complete Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
FPT
parameterized by #goods or #agents
BBN'16
Undirected Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
FPT
parameterized by #goods or #agents
Undirected Graphs
Goal: Determine the existence of a
efficient and locally envy-free allocation.
W[1]-hard
parameterized by #goods or #agents
Takeaway
Localized notions of envy...
are a natural and less restrictive model.
Takeaway
undirected graphs
v/s
directed graphs
some contrasts, some similarities...
Outline
Reductions: a framework for showing hardness
Historically
annoying
problem
Our
annoying
problem
\(\leq\)
Recipe for solving
well-known annoying problem (e.g, SAT)
via any hypothetical algorithm (A) for solving problem X:
Step 2. Run the algorithm A on q. Output → o
Step 3. Return o. Profit. 💸
👀
Step 1. Reduce instance of SAT to instance of X ↔ q
💥
Cutting \( \ell \) vertices
Given a graph \( G \), partition its vertex set into three parts: \( (X \cup S \cup Y) \) so that:
a) \( |S| \leq k \)
b) \( |X| = \ell \)
c) There are no edges between \( X \) and \( Y \).
\( \Downarrow \)
\( G \)
\( S \)
\( Y \)
\( X \)
n happy agents
n greedy agents
one trigger agent
n happy agents
n greedy agents
one trigger agent
n happy agents
n greedy agents
one trigger agent
...based on the structure of the graph \( G \)
\( \ell \) coveted items
...liked by all agents.
\( n - \ell + 1 \) greedy items
...liked by all greedy agents and the trigger agent.
\( \ell + k \) happy items
...liked by all happy agents.
n happy agents
n greedy agents
one trigger agent
...based on the structure of the graph \( G \)
n happy agents
n greedy agents
one trigger agent
n happy agents
n greedy agents
one trigger agent
n happy agents
n greedy agents
one trigger agent
😡
n happy agents
n greedy agents
one trigger agent
😡
n happy agents
n greedy agents
one trigger agent
😎
n happy agents
n greedy agents
one trigger agent
😎
😕
😕
😕
😕
😕
😕
n happy agents
n greedy agents
one trigger agent
😎
😕
😕
😕
😕
😕
😕
n happy agents
n greedy agents
one trigger agent
😎
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Are any of the happy agents jealous?
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
They don't envy the 😀-agents, since they don't value the good.
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Some of them will envy the agents who got the coveted goods .
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Some of them will envy the agents who got the coveted goods .
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Agents in \( X \cup S \) will envy the agents who got the coveted goods .
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Agents in \( X \cup S \) will envy the agents who got the coveted goods .
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
Agents in \( X \cup S \) will envy the agents who got the coveted goods .
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
n happy agents
n greedy agents
one trigger agent
😎
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
😀
Takeaway
undirected graphs
v/s
directed graphs
some contrasts, some similarities...
Outline
future work
Open problems
Is the problem of finding efficient and locally envy-free allocations in XP when parameterized by the vertex cover of the underlying social network?
FAIRNESS CONCEPTS
Note that whenever existence is guaranteed with respect to complete graphs, it is also guaranteed with respect to any social network.
Valuations
Our study focused completely on 0/1 valuations. More general valuations, including chores, would be interesting to study further!