Adversarial Search
& Games



What kinds of games are we playing?
No randomness: no rolls of die or random shuffles.
Two players and turn-based.
Zero sum.
Perfect information.
Ingredients of a game
Board and pieces (the setup).
The rules describing possible moves.
A win condition.
Want algorithms for calculating a strategy which
recommends a move from each state.
Ingredients of a game
A number \(N\), initially 0.
Add any number up to 10 to the current number.
The player who reaches the state 100 wins.
Want algorithms for calculating a strategy which
recommends a move from each state.
Reach 100
Board and pieces (the setup).
The rules describing possible moves.
A win condition.
Ingredients of a game
Let's look at some other examples.
What does it mean to solve a game?
Fully solve a game.
No matter what position you are in,
you know if you can force a win or a draw, and how.
Weakly solve a game.
Both the result and a strategy for achieving it
from the start of the game are known.
Ultra-weakly solve a game.
The perfect-play result, but not a strategy for achieving that value,
is known, like in Hex or Chomp.
Ingredients of a game
\(S_0\) : The initial state, which specifies how the game is set up at the start.
Player\((s)\): Defines which player has the move in a state.
Actions\((s)\) : Returns the set of legal moves in a state.
\(\operatorname{Result}(s, a)\) : The transition model, which defines the result of a move.
\(\operatorname{Terminal-Test}(s)\) : A terminal test, which is true when the game is over and false otherwise. States where the game has ended are called terminal states.
\(\operatorname{Utility}(s, p)\): A utility function, defines the final numeric value for a game that ends in terminal state \(s\) for a player \(p\).
Ingredients of a game
Traditionally: min v. max (2 players)
The min player is trying to minimize the utility.
The max player is trying to maximize the utility.
Zero-sum: utilities sum to zero and one player's gain is the other's loss
A Game Tree
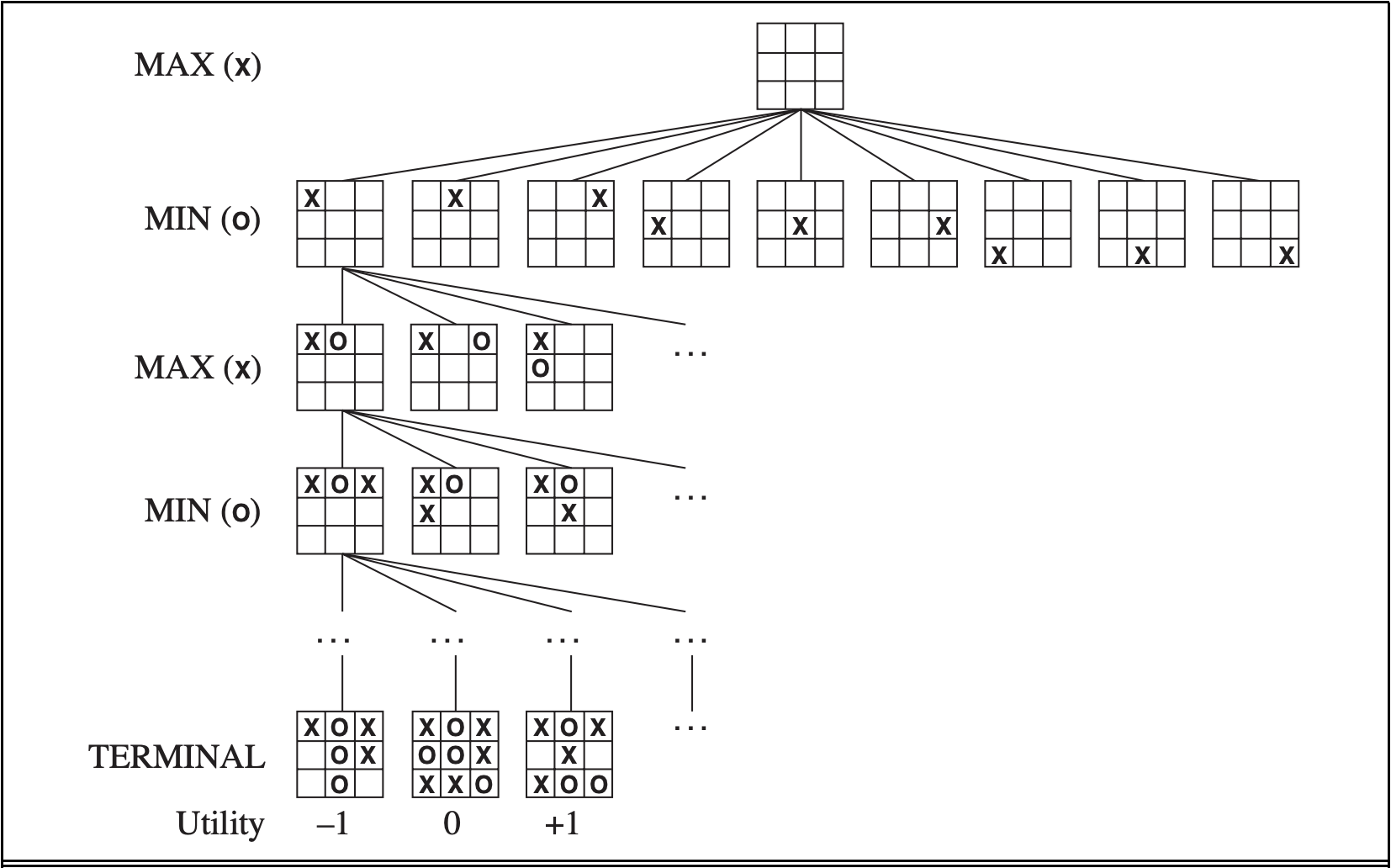
12
11
10
9
10
9
8
8
7
6
9
8
7
state
4
3
2
1
2
0
1
0
1
0
0
0
1
0
0
state
4
3
2
1
2
0
1
0
1
0
0
0
1
0
0
-1
1
-1
-1
1
1
1
1
-1
-1
1
-1
1
1
1
utilities
The Min-Max Algorithm
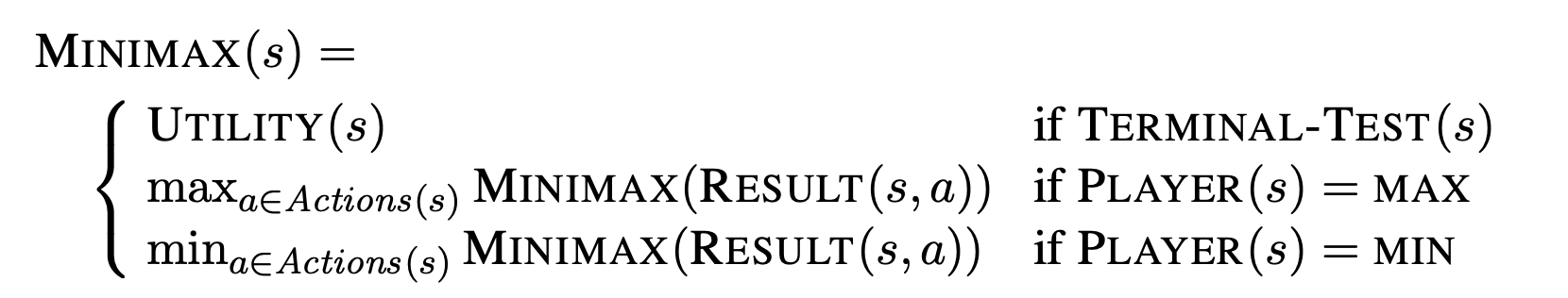
The Min-Max Algorithm
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig
This definition of optimal play for MAX assumes that MIN also plays optimally.
What if MIN does not play optimally?
Then MAX will do at least as well as against an optimal player, possibly better.
However, that does not mean that it is always best to play the minimax optimal move when facing a suboptimal opponent.
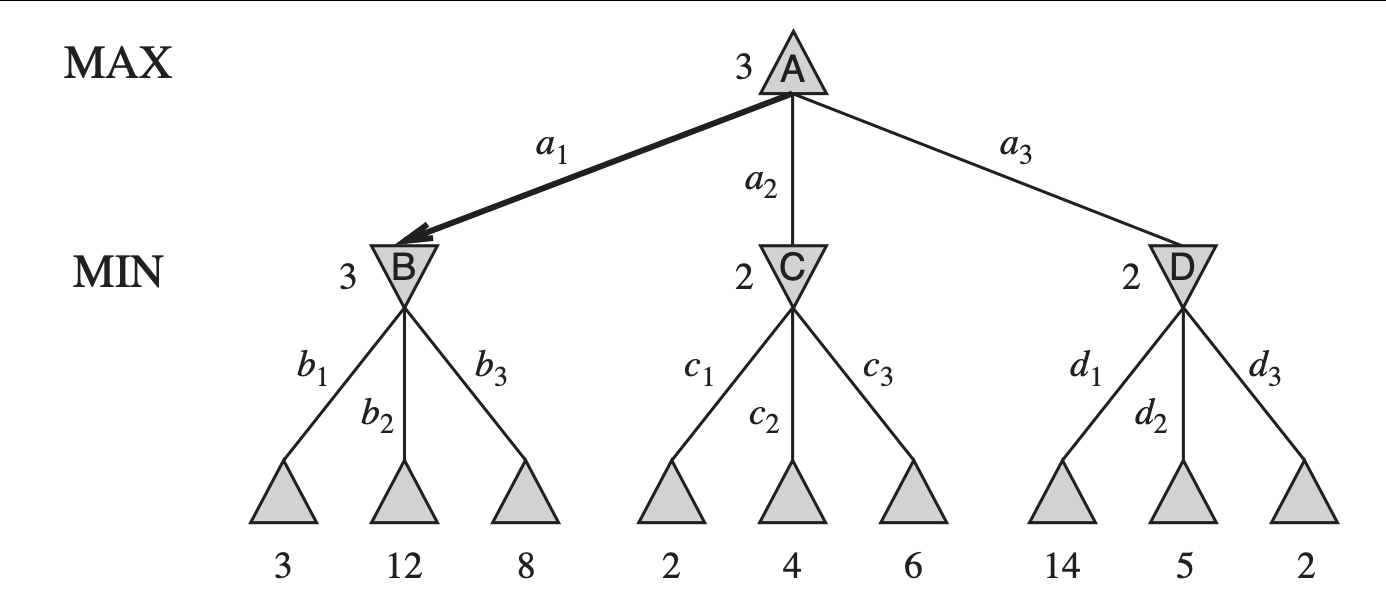
The minimax algorithm performs a complete depth-first exploration of the game tree.
If the maximum depth of the tree is \(m\) and
there are \(b\) legal moves at each point,
then the time complexity of the minimax algorithm is \(O\left(b^m\right)\).
The space complexity is \(O(m)\), proportional to the depth of the tree.
The exponential complexity makes Minimax impractical;
for example, chess has a branching factor of about 35
and the average game has depth of about 80 moves,
and it is not feasible to search \(35^{80} \approx 10^{123}\) states.
\([-\infty,+\infty]\)
\([-\infty,+\infty]\)
\([-\infty,+\infty]\)
\([-\infty,+\infty]\)
\([-\infty,+\infty]\)
\(3\)
\([-\infty,+\infty]\)
\([-\infty,+\infty]\)
\(3\)
???
\([-\infty,+\infty]\)
\([-\infty,3]\)
\(3\)
\([-\infty,+\infty]\)
\([-\infty,3]\)
\(3\)
\(12\)
\([-\infty,+\infty]\)
\([-\infty,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
???
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,+\infty]\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,+\infty]\)
\(2\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,+\infty]\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,+\infty]\)
\(14\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,14]\)
\(14\)
\([3,+\infty]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,14]\)
\(14\)
???
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,14]\)
\(14\)
\([3,14]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,14]\)
\(14\)
\(?\)
\([3,14]\)
\([3,14]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,14]\)
\(14\)
\(5\)
\([3,14]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,5]\)
\(14\)
\(5\)
\([3,5]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,5]\)
\(14\)
\(5\)
\([3,5]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([-\infty,5]\)
\(14\)
\(5\)
\(2\)
\([3,5]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([2,2]\)
\(14\)
\(5\)
\(2\)
\([3,3]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([2,2]\)
\(14\)
\(5\)
\(2\)
\([3,3]\)
\([3,3]\)
\(3\)
\(12\)
\(8\)
\([-\infty,2]\)
\(2\)
\([2,2]\)
\(14\)
\(5\)
\(2\)
Does the order of discovery matter?
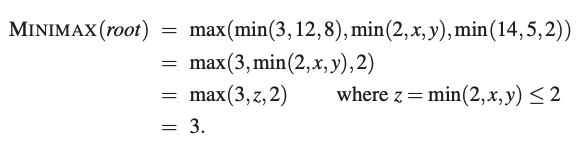
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig


Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow \bot\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow \bot\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow \bot\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)
\(v \longleftarrow +\infty\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)
\(v \longleftarrow +\infty\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow \bot\)
\(a2 \longleftarrow \bot\)
\(v \longleftarrow +\infty\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow +\infty\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow +\infty\)
\([-\infty,+\infty]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 8\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 12\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 12\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 12\)
\(a2 \longleftarrow \star\)
\(v \longleftarrow 3\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 12\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow -\infty\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([-\infty,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow +\infty\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow +\infty\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 3\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow +\infty\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow +\infty\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow +\infty\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow 2\)
\([3,+\infty]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow 2\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow 2\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\(v \longleftarrow 2\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,2]\)


\([3,+\infty]\)
\([\alpha,\beta]\)
\(v \longleftarrow 3\)
\(v2 \longleftarrow 2\)
\(a2 \longleftarrow \star\)
\([-\infty,3]\)
\([3,2]\)
Exercise: complete the last branch.

Initialization
Other Considerations
Multiplayer Games
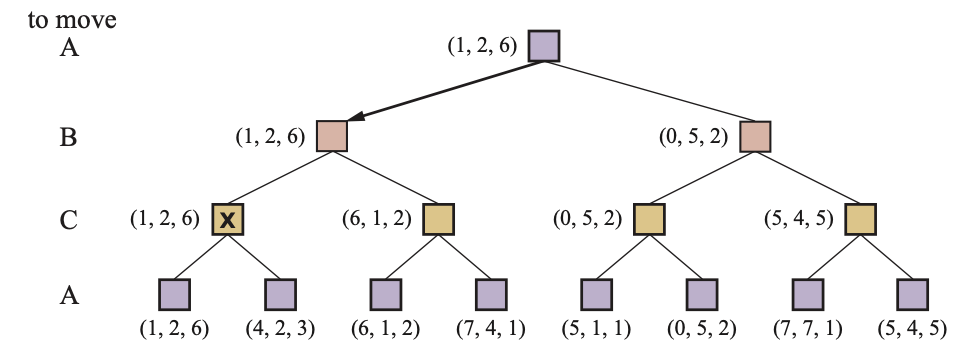
Food for thought: collusion/alliances, non zero-sum
payoff vectors: \(\langle u_A, u_B, u_C \rangle\)
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig
Heuristic Alpha-Beta Tree Search
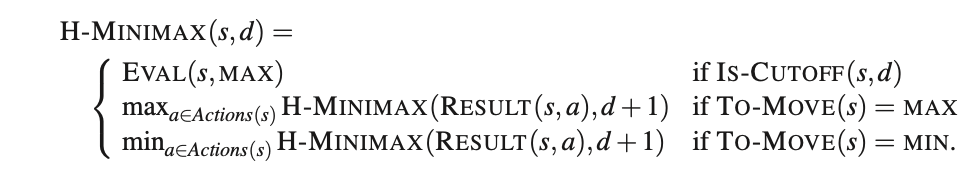
A heuristic evaluation function \(\operatorname{EVAL}(s, p)\) returns an estimate of the expected utility of state \(s\) to player \(p\).
For terminal states, it must be that
\(\operatorname{EVAL}(s, p)=\operatorname{UTILITY}(s, p)\).
For nonterminal states, the evaluation must be somewhere between a loss and a win:
\(\operatorname{UTILITY}(\)loss, \(p\)) \(\leq\) \(\operatorname{EVAL}(s, p) \leq \operatorname{UTILITY}(\) win,\(p)\).
Other Considerations
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig
Other Considerations
Heuristic Alpha-Beta Tree Search
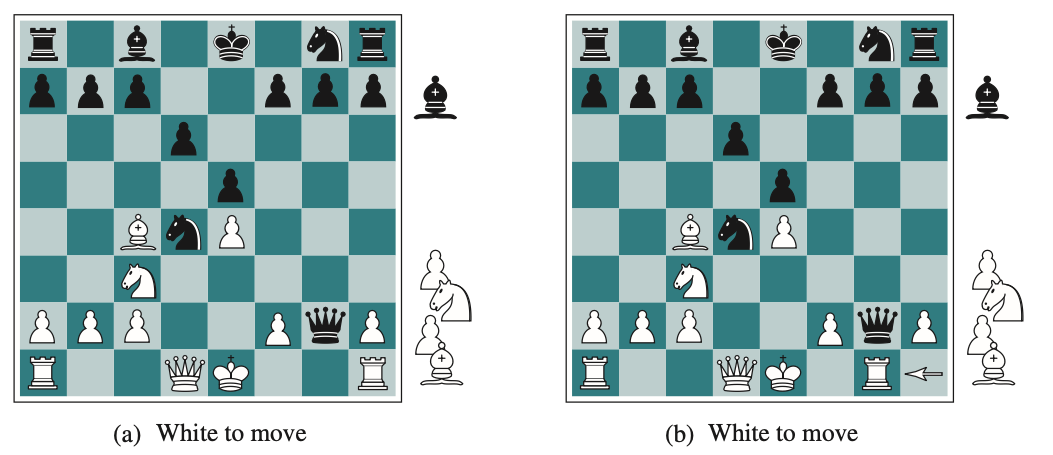
Source: Artificial Intelligence: A Modern Approach, Fourth Edition. Russell and Norvig
Other Considerations
Monte-Carlo Tree Search
Games of Chance
Partially Observable Games