Random circuit sampling using fermionic linear optics

PRX Quantum 3, 020328 (2022)

Michał Oszmaniec, ND, Mauro E. Morales, Zoltán Zimborás

The 5th Bangkok Workshop on Discrete Geometry, Dynamics and Statistics

24 Jan 2023

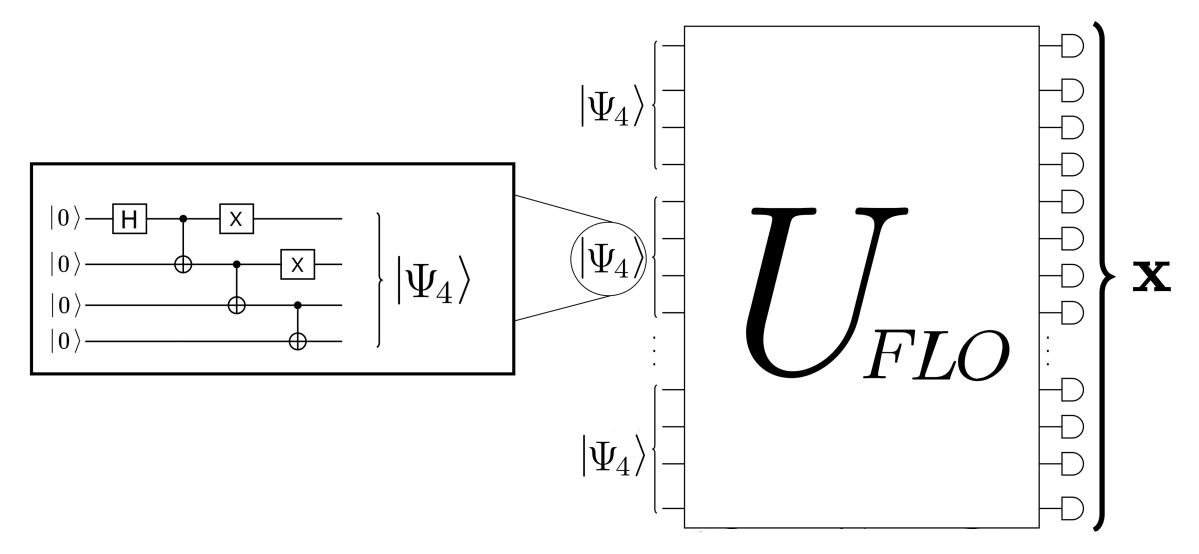
Matchgates!

Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\),

are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?

  • Fundamental limit of classical computation

  • Direct applications are few and far between

    • Certified random number generator (Aaronson)
    • Company/Lab PR

pc: Reuters

  • Introduction - What is a simulation?
  • Proof strategy for classical intractability
  • The fermionic case

Outline

{\bf y} \in \{0,1\}^n

String of \(n\) bits

\implies

Classical vs Quantum circuit

{\bf x}

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

\implies

String of \(n\) qubits

\bigotimes_{j=1}^n |\psi_j\rangle

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

\implies

Classical vs Quantum circuit

\implies

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

The result of the coin flips are just hidden bitstrings that can be included as extra inputs

Classical vs Quantum circuit

  • Every Boolean circuit can be composed out of elementary gates in a universal gate set
  • Most functions need an exponential-size circuit (Shannon)
  • Every quantum circuit can be composed out of elementary gates in a universal gate set
  • Most unitaries need an exponential-size circuit

Strong vs Weak Simulation

Strong simulation

Weak simulation

Can compute \(p_{\bf x}\) 

Can sample from \(p\)

|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x}
\sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon

In practice, there need to be some notions of errors

In this talk, I will use these definitions of strong and weak simulation unless stated otherwise

Relative error

Additive error

Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\), are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?

Given an initial state \(|\psi\rangle\) and a family of polynomial-depth quantum circuits \(\{U_{\alpha}\}_{\alpha}\), can there be a classical machine that approximately samples from \(p_{\bf x} = |\langle{\bf x}|U_{\alpha}|\psi\rangle|^2\) in poly\((n,\epsilon^{-1})\) time?

  • Introduction - What is a simulation?
  • Proof strategy for classical intractability
  • The fermionic case

Outline

Proof of Classical Intractability

Given \(|\psi\rangle, \{U_{\alpha}\}_{\alpha}\)

If the RHS task is #P-hard, then \(\mathcal{C}^{\mathrm{NP}}\) would be able to solve a #P-hard problem, which we believe to be impossible

Classical sampler \(\mathcal{C}\)

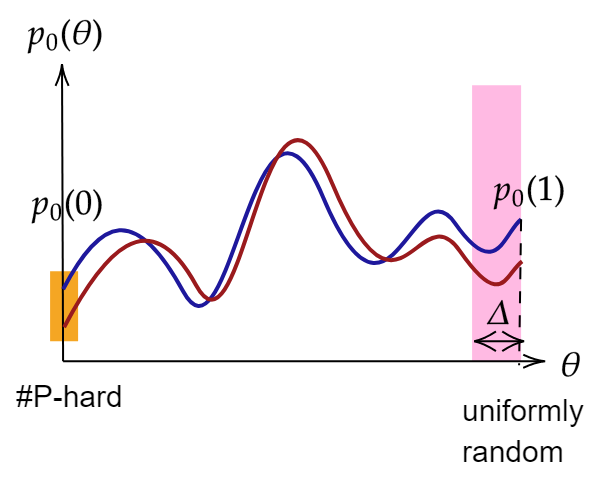
\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon

Anti-concentration of \(p_{\bf x}(U_{\alpha})\)

Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|U_{\alpha}|\psi\rangle|^2\) for most \(U_{\alpha}\)

\mathcal{C}^{\mathrm{NP}}
|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}

Anti-concentration

To turn relative error to additive error, we need most probabilities to be large

|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x} \longleftrightarrow \sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon
\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{C_1}{2^n}}\right) \ge C_2

\(l^2\)-distance to the uniform distribution:

\(\Vert  p-p_{\mathrm{unif}}\Vert^2 = Z - \displaystyle{\frac{1}{2^n}} = Z-Z_{\mathrm{unif}}\)

Z = \mathbb{E}_U \mathbb{E}_{\bf x}\, [ p^2_{\bf x}(U)]
Z \le \displaystyle{\frac{1}{\alpha 2^n}}

\(p_{\bf{x}}(U)\) anti-concentrates if

Z_{\mathrm{unif}} = \displaystyle{\frac{1}{2^n}}

Implies \(\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{\beta}{2^n}}\right) \ge \alpha(1-\beta)^2 \) via the Paley-Zygmund inequality

\Pr\left( X\ge \beta\mathbb{E}[X] \right) \ge (1-\beta)^2 \displaystyle{\frac{\mathbb{E}[X]^2}{\mathbb{E}[X^2]}}
2
2
2

Anti-concentration

Modified from Dalzell et al., PRX Quantum 2022

Average-Case Hardness

  • Average-case hardness for Boson Sampling originates from the argument for average-case hardness to compute the permanent via polynomial interpolation (Lipton 1991).
  • Bouland et al., Nat Phys (2018) and Movassagh 2019 import the argument to Random Circuit Sampling

Worst-case hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\)

Worst-to-average-case reduction

Hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\) for most \(U_{\alpha}\)

Easy to argue based on existing results in quantum computing

  • Introduction - What is a simulation?
  • Proof strategy for classical intractability
  • The fermionic case

Outline

Rio Grande, 2017

Fermionic Linear Optics (FLO)

X = \begin{pmatrix}0&1\\1&0 \end{pmatrix}
Y = \begin{pmatrix}0&\!\!\!-i\\i&0 \end{pmatrix}
Z = \begin{pmatrix}1&0\\0&\!\!\!-1 \end{pmatrix}

Reminder

\sigma^{\dagger} = X-iY = \begin{pmatrix}0&0\\1&0 \end{pmatrix}
\sigma^{\dagger}|0\rangle = |1\rangle

Identify computational basis states with occupation number states

Jordan-Wigner

f_j f^{\dagger}_k +f^{\dagger}_k f_j = \delta_{jk}\mathbb{I}
(f^{\dagger}_j)^2 = 0

CAR

f^{\dagger}_j \coloneqq \sigma_j^{\dagger} \displaystyle{\prod_{k=1}^{j-1}} Z_k

\(f_j^{\dagger}\) creates a fermion at site \(j\)

Pauli exclusion

Fermionic Linear Optics (FLO)

m_j^X \coloneqq X_j \displaystyle{\prod_{k=1}^{j-1}} Z_k
m_j^Y \coloneqq Y_j \displaystyle{\prod_{k=1}^{j-1}} Z_k

cf. Dirac's gamma matrices

m_{\alpha}m_{\beta} + m_{\beta}m_{\alpha} = 2 \delta_{\alpha\beta} \mathbb{I}
\alpha = (j,X\,\mathrm{or}\,Y)

Majoranas

\begin{pmatrix} 1 & & 0 \\ & \!\!\!\!\!\Large{-iX}\!\!\!\! \\ 0 & & 1 \end{pmatrix}

Non-example

\mathrm{SWAP}= \mathbb{I}\!\otimes\!\mathbb{I}\!+\!X\!\otimes\! X \!+\! Y\!\otimes \!Y \!+\! Z\!\otimes \!Z

\(Z\!\otimes\! Z\) interaction is not FLO

FLO Hamiltonians are quadratic

Antisymmetric

H_{\mathrm{FLO}} = \displaystyle{\frac{i}{4}} \sum_{\substack{\alpha,\beta \\ \alpha>\beta}} h_{\alpha\beta} [m_{\alpha},m_{\beta}]
=\begin{pmatrix} R^{\dagger}_Z(\varphi)_{11} & & R_Z^{\dagger}(\varphi)_{12} \\ & \!\!\!\!\!\Large{R_X(\theta)}\!\!\!\! \\ R_Z^{\dagger}(\varphi)_{21} & & R_Z^{\dagger}(\varphi)_{22} \end{pmatrix}

Fermionic Linear Optics (FLO)

Even parity

Odd parity

M(U^+,U^-) =\begin{pmatrix} U^+_{11} & & U^+_{12} \\ & \Large{U^-} \\ U^+_{21} & & U^+_{22} \end{pmatrix}
\det U^+ = \det U^-

FLO gates AKA Matchgates

(Valiant, SIAM J Comput 2002)

\mathrm{SWAP} = \begin{pmatrix} 1 & & 0 \\ & \!\!\!\!\Large{X}\!\!\! \\ 0 & & 1 \end{pmatrix}

Non-example

Google AI Blog

\mathrm{fSim}(\theta,\varphi) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -i\sin\theta & 0 \\ 0 & -i\sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & e^{-i\varphi} \end{pmatrix}

Classical Intractability?

Classical sampler \(\mathcal{C}\)

\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon

Anti-concentration?

Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|V_{\mathrm{FLO}}|{\bf 0}\rangle|^2\) for most \(V_{\mathrm{FLO}}\)

\mathcal{C}^{\mathrm{NP}}
|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}
V_{\mathrm{FLO}}

This is easy!

Fermionic Linear Optics (FLO)

\vec{m}(t) = V^{\dagger} \vec{m} V = e^{{\bf h}t} \vec{m}

Generators of rotations SO(\(2n\))

V_{\mathrm{FLO}} = e^{iH_{\mathrm{FLO}}t}

(Defining representation)

Antisymmetric

Manipulating \(2n\times 2n\) matrices instead of \(2^n\times 2^n\) matrices!

  • Only need to specify the correlation matrix (2nd moments)
  • All higher moments can be extracted from \(\Sigma\) via Wick's theorem
\Sigma_{\alpha\beta} \coloneqq \frac{i}{2}\mathrm{Tr}(\rho[m_{\alpha},m_{\beta}])
p_{\bf x} = \frac{1}{i^{2^n}} \mathrm{Pf} (\Sigma)

\(\rho = (|0\rangle\langle 0|)^{\otimes n}\) is a fermionic Gaussian state

Fermion Sampling

  • FLO with computational-basis input state admits strong simulation (compute \(p_{\bf x}\) up to logarithmic number of decimals)
  • Not the case with non-Gaussian (magic) input state; strong simulation is #P-hard (cf. Ivanov, PRA 2017)
  • Our work shows that weak simulation is also hard
V_{FLO}
|\Psi_4\rangle = \displaystyle{\frac{|0011\rangle + |1100\rangle}{\sqrt{2}}}
\mathbb{E}_V [p^2_{\bf 0}] = \int dV\, \mathrm{Tr}(V|\Psi\rangle \langle \Psi| V^{\dagger}|{\bf 0}\rangle\langle {\bf x}|)^2
= \mathrm{Tr}(|\Psi\rangle \langle \Psi| \int dV\, V^{\dagger}|{\bf 0}\rangle\langle {\bf 0}|V)^2
= \mathrm{Tr}\left[(|\Psi\rangle \langle \Psi|)^{\otimes 2} \underbrace{\int dV\, (V^{\dagger})^{\otimes 2}(|{\bf 0}\rangle\langle {\bf 0}|)^{\otimes 2}V^{\otimes 2}}\right]

Sum of projectors onto irreps by Schur's lemma under nice conditions 

  • SO(\(2n\)) for FLO
  • U(\(n\)) for passive (number-preserving) FLO

Anti-concentration

\mathrm{Tr} \left[\mathbb{P}_{\mathrm{pas}} (|\Psi\rangle\langle\Psi |)^{\otimes 2}\right] \le \frac{1}{2N+1} \cdot \left[ 2 \sum_{k=0}^{N-1} {2N \choose k} \mathrm{Tr}(\rho_k^2) + {2N \choose N} \mathrm{Tr}(\rho_N^2) \right]

For example,

Then use combinatorics to bound the RHS

Worst-to-average-case reduction

  • There exists a "worst-case circuit" \(V_0\) for which \(p_{\bf 0} = |\langle \mathbf{0}|V_0|\Psi\rangle|^2\) is #P-hard to approximate
  • Deform to average-case (Haar random) circuits where \(p_{\bf 0} (\theta)= |\langle \mathbf{0}|V(\theta)|\Psi\rangle|^2\) is a polynomial of low-degree \(q\)
  • Sample \(\gtrsim q\) points (some can be errorneous\(\iff\)robustness) and recover \(p_{\bf 0}(\theta)\) via Berlekamp–Welch
  • Plug in \(\theta = 0\) to solve a #P-hard problem! 

Unitary Paths

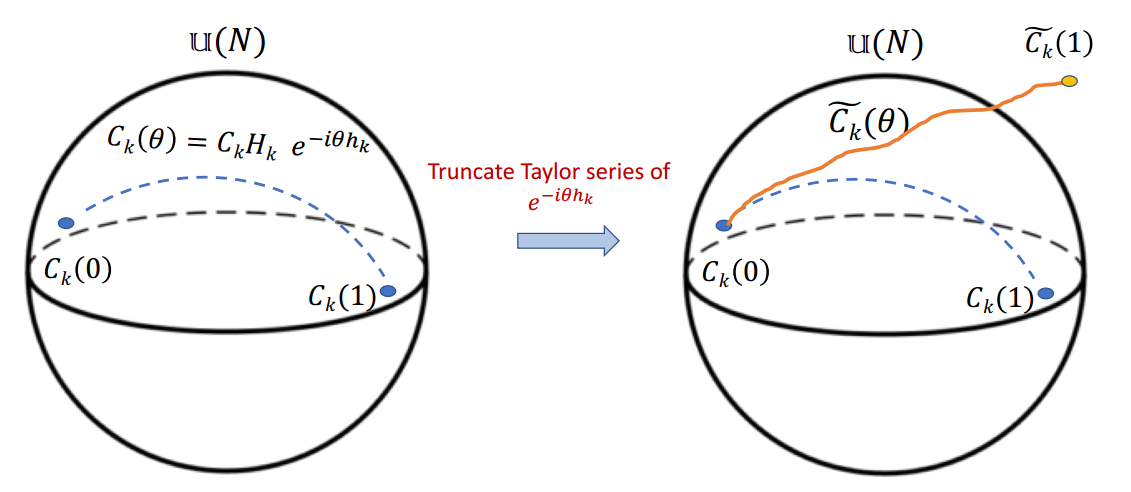
First idea: truncated exponential path

U(\theta) = U_0 e^{i\theta H}

Movassage 2019

= U_0 \left(\mathbb{I} + i\theta H + \frac{(i \theta H)^2}{2!} + \cdots \right)

Truncation gives rise to a non-unitary operator

f(X) = (\mathbb{I}-X)(\mathbb{I}+X)^{-1}
g_{\theta} = g_0 \displaystyle{ \frac{(1-\theta) \mathbb{I} +(1+\theta) g}{ (1+\theta) \mathbb{I} +(1-\theta)g }}

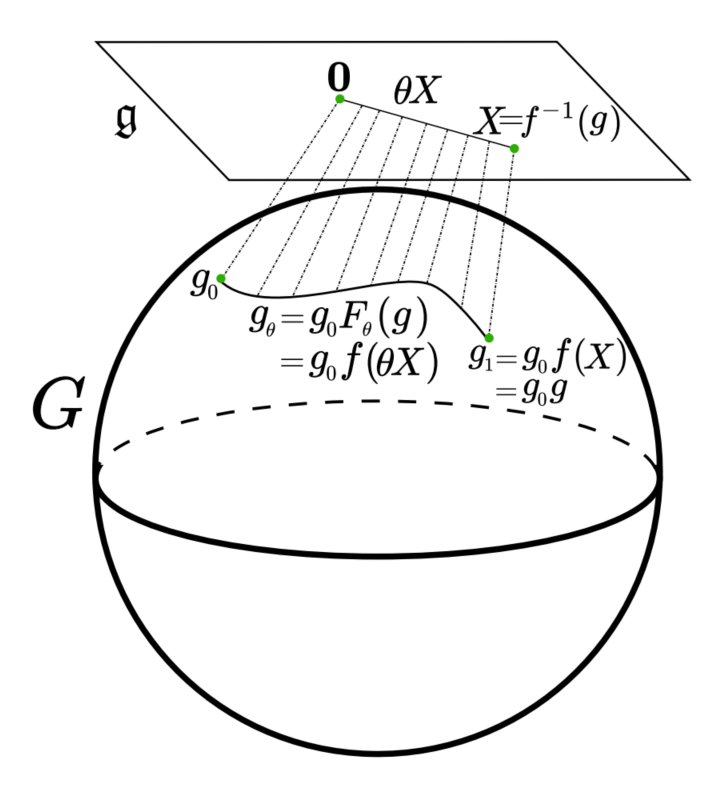
Better idea: Cayley path

Unitary

Hermitian

Hardness Guarantees

Quantum advantage scheme Robustness of avg-case hardness
(additive error)		 Anti-concentration
Boson Sampling
Random circuit sampling (Google layout)
Fermion Sampling
2^{-\tilde{O}(n)}
2^{-\tilde{O}(n^{1.5})}
2^{-\tilde{O}(n^2)}

Bouland et al., FOCS 2021

Other Results

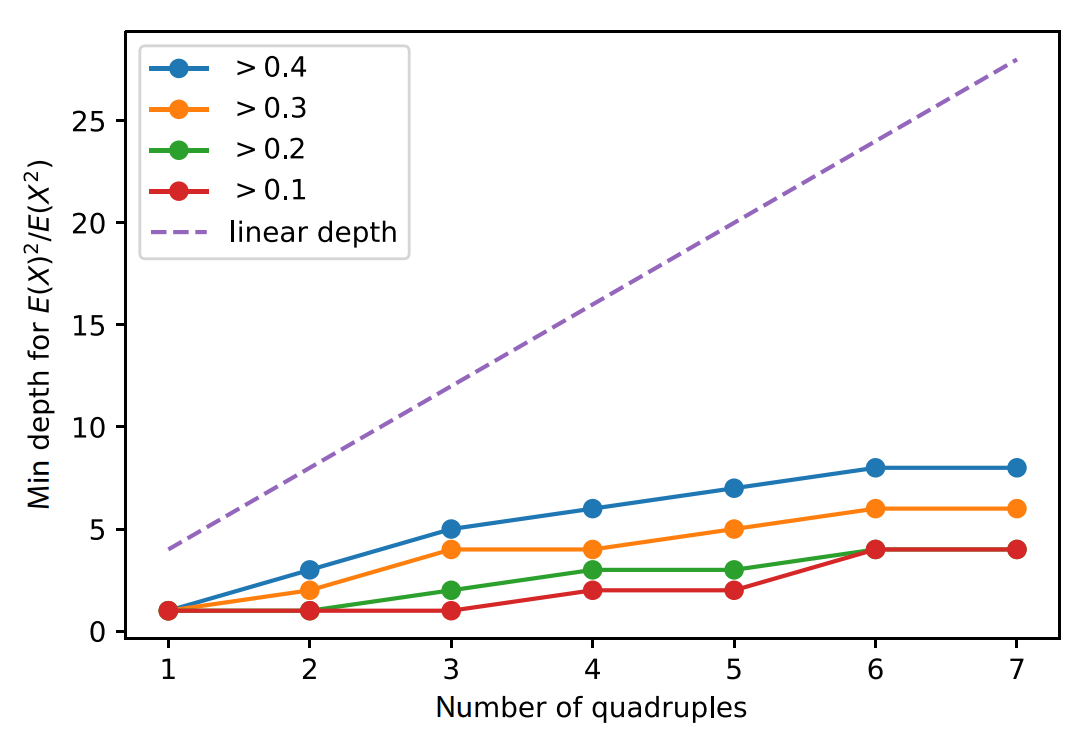
  • Numerics suggest that random FLO circuits anti-concentrate in sub-linear depth
|+_X^p\rangle \\ \text{or} \\ |+_Y^p\rangle
p,p' = 1,2,\dots,d
V_{FLO}
|+_X^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_X\rangle \otimes |0\rangle^{\otimes (n-p)}
|+_Y^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_Y\rangle \otimes |0\rangle^{\otimes (n-p)}
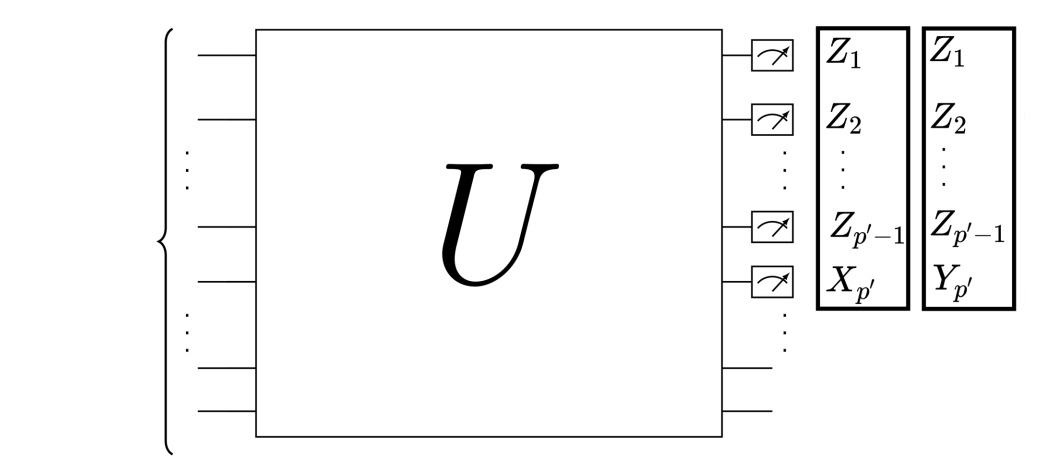
  • Assuming that the circuit is FLO, circuit tomography can be performed efficiently utilizing single-mode input states and product measurements

Summary

V_{FLO}
|\Psi_4\rangle = \displaystyle{\frac{|0011\rangle + |1100\rangle}{\sqrt{2}}}
  • Simulating \(U|\psi\rangle\) = Sampling from \(|\langle {\bf x}|U|\psi\rangle|^2\)
  • The standard argument for hardness of sampling requires statistical data of the ensemble \(\{U_{\alpha}\}_{\alpha}\)
  • When \(\{U_{\alpha}\}_{\alpha}\) has the structure of a low-dimensional Lie group, there are available techniques for computing these data
  • Low-dimensionality might lead to a fast classical algorithm; but this might be circumvented by a good choice of the initial state (here a non-Gaussian state)

Thank You!

↑ for the slides