Negative Quasi-Probability and Contextuality in Classical Simulations of Quantum Processes

นินนาท แดงเนียม

Center for Quantum Information and Control

Mahidol University, 29 December 2014

University of New Mexico

Quantum Supremacy

Post-1994 Universal quantum computation, DQC1, IQP computing, Boson-Sampling...

Quantum Supremacy

What separates classical mundanity and quantum supremacy?

Important for both foundational and practical reasons

  • Exponentially many complex numbers?
  • Interference?

Quantum Supremacy

  • Negative probability?
  • Nonlocality?
  • Entanglement?
  • Discord?

Entanglement is Not Enough

Matrix product state formalism enables simulation of states with little entanglement.

Entanglement is a stronger-than-classical correlation studied intensively since the advent of quantum information science.

Entanglement is Not Enough

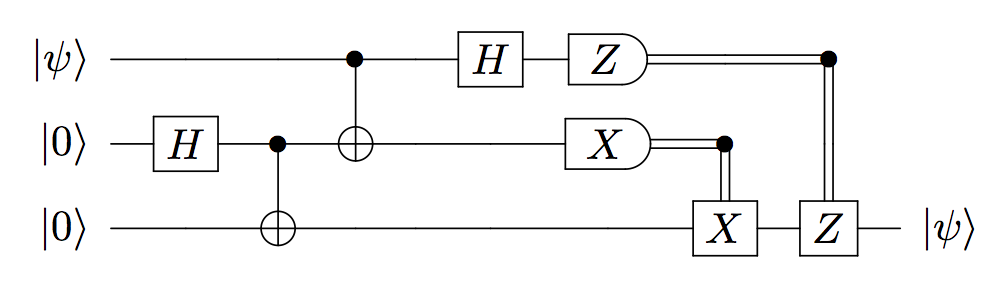
Teleportation circuit (with input states in the computational basis) can be simulated efficiently on a classical computer!

Entanglement is Not Enough

Strong simulation of qudit Clifford circuits

X|j\rangle = |j+1 \ mod\ p \rangle
X∣j⟩=∣j+1 mod p⟩
Z|j\rangle = \omega ^{j}|j\rangle
Z∣j⟩=ω​j​​∣j⟩
  • Heisenberg-Weyl operators
T_{x,z} = \omega ^{-2^{-1}xz} X^x Z^z
T​x,z​​=ω​−2​−1​​xz​​X​x​​Z​z​​
\omega = e^{2\pi i/p}
ω=e​2πi/p​​
  • Clifford operators = Normalizer of Weyl-Heisenberg operators
  • Stabilizer states = Orbit of the computational basis state under Clifford operations

Entanglement is Not Enough

Specifying (qubit) stabilizer states only requires

n(2n+1)
n(2n+1)

bits

Stabilizer generators

Each Weyl-Heisenberg operator

Entanglement is Not Enough

Physics explanation: there is a hidden variable representation in which stabilizer circuits do not generate "negative probability"

Quasi-Probability Representations

A QPR consists of a frame F, a dual frame D (Hermitian (possibly overcomplete) bases) and a 1-1 map from operators to distributions

\rho \to W_{\rho}(\lambda) = Tr(\rho F(\lambda))
ρ→W​ρ​​(λ)=Tr(ρF(λ))
E \to W_{E}(\lambda) = Tr(E D(\lambda))
E→W​E​​(λ)=Tr(ED(λ))

so that the Born rule becomes the law of total probability

Tr(\rho E) = \sum_{\lambda} W_E (\lambda) W_{\rho} (\lambda) = \sum_{\lambda} P(E|\lambda)P(\lambda).
Tr(ρE)=∑​λ​​W​E​​(λ)W​ρ​​(λ)=∑​λ​​P(E∣λ)P(λ).

D can be defined by the reconstruction formula

\rho = \sum_{\lambda} Tr(\rho F(\lambda))E(\lambda)
ρ=∑​λ​​Tr(ρF(λ))E(λ)

Allow classical simulation techniques when W is non-negative!

Quasi-Probability Representations

The discrete Wigner representation

\phi_{\rho} (x,z) = \langle T_{x,z}\rangle
ϕ​ρ​​(x,z)=⟨T​x,z​​⟩
W_{\rho} (q,p) = \frac{1}{d}\sum_{x,z=0}^{d-1} \omega^{xq+zp} \phi_{\rho}(x,z)
W​ρ​​(q,p)=​d​​1​​∑​x,z=0​d−1​​ω​xq+zp​​ϕ​ρ​​(x,z)
  • Hudson's theorem: a pure state is non-negative if and only if it is a stabilizer state.
  • Clifford operations act as permutations, in particular they preserve positivity.
  • There are doubly exponentially more stabilizer states in n d-dimensional Wigner representation than in a single d^n-dimensional Wigner representation

Simulation of Clifford circuits with positive Wigner representation

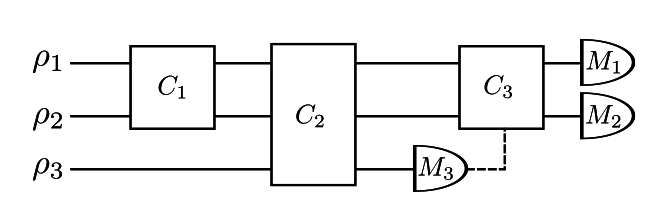
Veitch et al., Negative Quasi-Probability as a Resource for Quantum Computation

Weak simulation

Simulation of Clifford circuits with positive Wigner representation

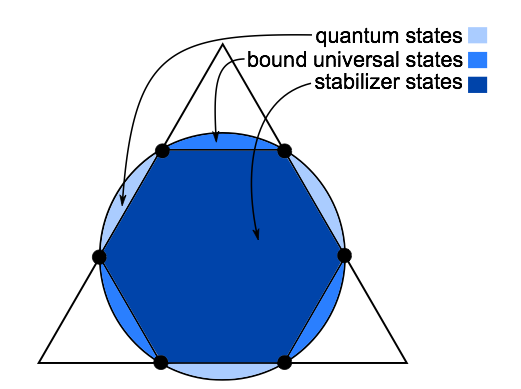
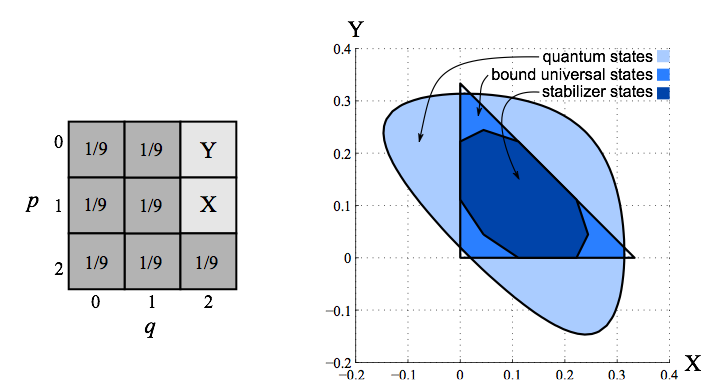
Veitch et al., Negative Quasi-Probability as a Resource for Quantum Computation

Contextuality

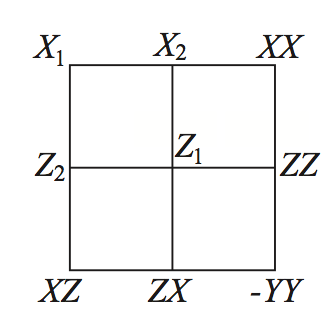
Mermin-Peres square

  • Measurement contextuality
  • Preparation contextuality = Occurrence of negative quasi-probability

Take-Home Messages

Negative Wigner representation hence contextuality is necessary for universal quantum computation in the circuit model.

Phase space techniques and quantum foundations extend and explain results in quantum information science.

Quantum information science provides operational meaning of "quantumness" in negative Wigner representation in quantum optics

Related Works

  • Measurement-based quantum computation
  • Similar result in rebit (real qubit) quantum computation
  • Continuous class of simulatable states?

Thank You!