Toward a Classical Subtheory for Matchgate Circuits

Center for Quantum Information and Control, University of New Mexico

Ninnat Dangniam, Chris Ferrie

Centre for Engineered Quantum Systems, The University of Sydney

CQuIC, 20 April 2016

Known to be

classically

simulatable

Universal

?

Gaussian

Universal

?

Matchgate/Fermionic Quantum Computation

Bravyi quant-ph/0511178

de Melo, Ćwikliński, Terhal 1208.5334

Oszmaniec, Gutt, Kuś 1406.1577

Matchgates

G(A,B)= \begin{pmatrix} A_{11} & 0 & 0 & A_{12} \\ 0 & B_{11} & B_{12} & 0 \\ 0 & B_{21} & B_{22} & 0 \\ A_{21} & 0 & 0 & A_{22} \\ \end{pmatrix}
\det A = \det B

or

A,B \in \text{SU}(2)
\text{SWAP}= \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix}
\det I \neq \det X
X \notin \text{SU}(2)

Non-Example

\{ \cdot,\cdot \}

Anti-commutator

\{ c_{\alpha}, c_{\beta} \} = 2 \delta_{\alpha \beta}
c_1 = X_1
c_2 = Y_1
c_{2j-1} =
c_{2j} =

Qubits-Fermionic Modes Isomorphism

\prod_{k=1}^{j-1} Z_k
\prod_{k=1}^{j-1} Z_k
X_j
Y_j

Majorana or Jordan-Wigner operators

Qubits-Fermionic Modes Isomorphism

|0 0 \cdots 0 \rangle \mapsto |\bold{x}\rangle := | x_1 x_2 \cdots x_n \rangle
\{ a^{\dagger}_j, a_k \} = \delta_{jk}
a_j = c_{2j-1} + ic_{2j}

Computational basis states = Number states

Nonlocality

  1. N.N. Matchgates

  2. Non-N.N. Matchgates

  3. All quadratic Hamiltonians

Examples

Nonlocality

|0\rangle
|0\rangle
|0\rangle

N.N. Matchgates

c_1,c_2,c_3,c_4

Quadratic Hamiltonians with adjacent modes

G(A,B)

6 Generators

ZI
IZ
XX
YY
YX
XY

Nonlocality

|0\rangle
|0\rangle
|0\rangle

Non-N.N. Matchgates

Quartic Hamiltonians

(Universal)

G(A,B)
c_1,c_2,c_3,c_4,c_5,c_6

Nonlocality

|0\rangle
|0\rangle
|0\rangle

Non-N.N. Matchgates

G(A,B)

Quartic Hamiltonians

(Universal)

c_1,c_2,c_3,c_4,c_5,c_6

Nonlocality

|0\rangle
|0\rangle
|0\rangle

>2-qubit gate

c_1,c_2,c_5,c_6

Quadratic Hamiltonians with nonadjacent modes

Nonlocality

|0\rangle
|0\rangle
|0\rangle

N.N. matchgates

c_1,c_2,c_5,c_6

Quadratic Hamiltonians with nonadjacent modes

G(A,B)
G(Z,X)
\cdots
G(Z,X)
c_{2j-1} \leftrightarrow c_{2j+1}
c_{2j} \leftrightarrow c_{2j+2}
|\psi \rangle |0\rangle \leftrightarrow |0\rangle |\psi \rangle

Modal swap

Conditional swap

\mathcal{O}(n^3)

Classical Simulation

(Hand-Waving)

  1. The       's evolve linearly
  2. The outcome probability can be found from the determinant
c_{\alpha}

Classical Simulation

(Hand-Waving)

1. Linearity

U^{\dagger}
U
c_{\alpha}
= \sum_{\beta}
R_{\alpha \beta}
c_{\beta}
\text{SO}(2n)

rotation

Quadratic Hamiltonian

\tilde{c}_{\alpha} =

(Symplectic for bosons)

Classical Simulation

(Hand-Waving)

k \le n
U^{\dagger}
U
\prod_{j = y_1}^{y_k} a^{\dagger}_j a_j
P(\bold{y}|\bold{x}) = \langle 0|
|0\rangle = \text{Pf}(M)

2. Counting a subset of              fermions (Z measurements on k qubits)

\text{Pf}^2 (M) = \det (M)

Determinant is easy to calculate (unlike permanent for bosons)

Some poly-size antisymmetric matrix

Quantum States at all Time

= \frac{i}{2} \text{Tr} (\rho [c_{\alpha} , c_{\beta}])
V_{\alpha,\beta}

Covariance matrix

Gaussian states

i\tilde{c}_{2j-1} \tilde{c}_{2j})
= \frac{1}{2^n} \prod_{j=1}^n ( I +
\lambda_j

"Williamson eigenvalue" of

V
\rho
= N \exp{ \left( -i \bold{c}^T B \bold{c} \right)}

Example: number states

|\bold{x}\rangle \langle \bold{x}| = \prod_{j=1}^n \frac{I - \lambda_j ic_{2j-1} c_{2j}}{2}
\lambda_j = (-1)^{x_j}

Quantum States at all Time

Wick's theorem

\prod_{j=y_1}^{y_k} c_{2j-1} c_{2j} ) = \frac{1}{i^k} \text{Pf} (
) = \text{Tr}(
\rho
P(\bold{y}|
\rho
\vert_{\bold{y}})
V

Quantum States at all Time

  • Product input states - Single qubit Z measurement (Only linearity is required)

Variants of the Simulation Result

Jozsa, Miyake 0804.4050

  • Product input states - Product basis measurements

Brod 1602.03539

  • Simulating quadratic + linear Hamiltonians by quadratic Hamiltonians alone

Knill quant-ph/0108033

Jozsa, Miyake, Strelchuck 1311.3046

Product Input States - Product Basis Measurements

G(H,H)
|\psi \rangle |+\rangle \mapsto H|\psi \rangle |+\rangle

Conditional Hadamard

G(Z,X)
|\psi \rangle |0\rangle \leftrightarrow |0\rangle |\psi \rangle

Conditional swap

|0\rangle
|0\rangle
|+\rangle
G(Z,X)
G(H,H)
\cdots
G(R_z,R_z)
G(-Z,X)
|\psi \rangle |1\rangle \leftrightarrow |1\rangle |\psi \rangle
Z
G(\pm Z,X)

Quasi-Probabilities

|0\rangle
|0\rangle
|0\rangle
G(A,B)
G(A',B')
+
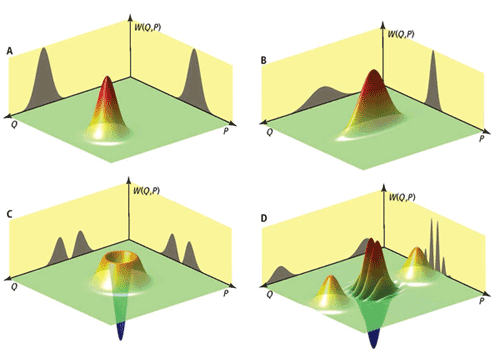
  1. Provide classical subtheory (hidden variable model) when quasi-probabilities are non-negative
  2. The negativity quantifies the resource for universal quantum computation

Why?

Classical Subtheory

\rho_c
E_c

Preparation

P(\lambda|\rho_{c})

Measurement

P(E_c|\lambda)
P(E_c|\rho_c) = \sum_{\lambda} P(E_c|\lambda)P(\lambda|\rho_c)
c =

classical

\lambda =

"true state of the world"

\rho_c
E_c

Preparation

\text{Tr}[\rho F(\lambda)]

Measurement

\text{Tr}[E D(\lambda)]
P(E|\rho) = \text{Tr} \{ E

(Phase Space) Quasi-Probability  Model

\sum_{\lambda} \text{Tr} [\rho F(\lambda)] D(\lambda)
\}
\sum_{\lambda} \text{Tr} [ \rho
F(\lambda)
]
D(\lambda)
= \rho

Frame

Dual Frame

(Phase Space) Quasi-Probability  Model

(Phase point operators)

  • Frame or dual frame must contain negative operators
  • Negativity quantifies the amount of resource

Spekkens 0710.5549

Ferrie, Morris, Emerson 0910.3198

Veitch et al. 1307.7171

Find a classical subtheory that contains Gaussian states and fermion-counting measurements

Mission

Group-Covariance

U^{\dagger} (g) F(\lambda) U (g) = F(g\lambda)
G

-action permute phase points

  • Sufficient to preserve positivity

Gross quant-ph/0602001

  • Also necessary in discrete Wigner functions in odd dimensions
  • Impossible for qubit discrete Wigner functions (Clifford covariance)

Zhu 1510:02619

Group-Covariance

  1. How?

  2. Which group?

Lie group

G

-covariant

G
F(\lambda,s)

BM

One-parameter family of

Brif, Mann quant-ph/9809052

Constructing G-Covariant Phase Spaces

D(\lambda,s) = F(\lambda,-s)
G

BM

Irrep

Fiducial state

U(g)
|\psi \rangle

Lie group

G/

Coset space

Input Data

Stabilizer of 

|\psi \rangle
H

Coset Space

\text{SO}(3)/\text{SO}(2) \simeq S^2

No "Good" SO(4)-covariant phase space

G(A,B)= \begin{pmatrix} A_{11} & 0 & 0 & A_{12} \\ 0 & B_{11} & B_{12} & 0 \\ 0 & B_{21} & B_{22} & 0 \\ A_{21} & 0 & 0 & A_{22} \\ \end{pmatrix}

Phase space separates into odd and even parity subspaces

A,B \in \text{SU}(2)

No "Good" SO(4)-covariant phase space

  • In each subspace, any two pure states are connected by an SU(2) transformation (matchgate)
  • So if there is just one positive pure state, then every pure state is positive.
  • This is impossible for self-dual representations
  • Dropping self-duality shouldn't help

The argument:

\text{SO}(2n+1)

BM

Quadratic + linear Hamiltonians

Fiducial state

|0 \rangle
\text{SO}(2n+1)/
\text{U}(n)

Number-preserving Hamiltonians

Input Data

|\lambda \rangle = U|0\rangle

Coherent states

Oeckl 1408.2760

BM

Input Data

Y_{l,m} (\lambda)
|\langle \lambda | \lambda' \rangle|^2 = \sum_{l,m}
\tau_{l,m}

Orthogonal functions on the coset space

Y^*_{l,m} (\lambda) Y_{l,m} (\lambda')
\tau_{l,m}
\text{SO}(2n+1)
/\text{U}(n)
D_{l,m} = \frac{1}{\sqrt{\tau_{l,m}}} \int_{G/H} Y_{l,m} (\lambda) | \lambda \rangle \langle \lambda |
F(\lambda,s) = \sum_{l,m} \frac{1}{\sqrt{ \tau_{l,m}^s}} Y^*_{l,m}(\lambda) D_{l,m}

BM

Heisenberg Group

  • Reps of Heisenberg group are projective reps of an abelian group 
  • Projective reps + F.T. on non-abelian finite groups is not enough to construct a quasi-probability representation

Dangniam, Ferrie 1410.5755

  • Does BM construction work on finite groups?
U = D_{l,m}
\text{SO}(2n+1)/\text{U}(n)

Hard

"Easy"

\text{SO}(m+1)/\text{SO}(m) \simeq S^m

"Easy"

\text{SO}(5)/\text{U}(2) \simeq \mathbb{C}P^3

Need "the ring of invariant differential operators"

Barut Theory of Group Representations

Finding

Y_{l,m}

Open Questions

  • Classical subtheory of SO(2n+1)-covariant phase space?
  • General Hudson's theorem for group-covariant phase space?
  • BM construction for finite groups?

Lie group

G

-covariant

G

BM

phase spaces

What I Thought It Would Be

Lie group

G

-covariant

G

BM

phase spaces

Mathematicians

What It Actually Is

Thank You