The Computational Power of Identical Particles

Ninnat Dangniam

Near-Term Quantum Computers Online Workshop

1 July 2020 

Ph.D. in physics, University of New Mexico (2018)

Postdoctoral researcher, Fudan University (Nov 2018 - Aug 2020)

Analog quantum supremacy

with Dimitris Angelakis' group (CQT, NUS)

  • arXiv:2002.11946

  • arXiv:2005.11222

Quantum state certification

with Huangjun Zhu (Fudan U)

Fermionic quasi-probability representation

with Carlton Caves & Chris Jackson (CQuIC, UNM)

Classical

Quantum

Does the computational process harness genuine quantum effects that cannot be replicated classically?

Classical simulation

Quantum advantage

?

photo credit

|0\rangle, |1\rangle

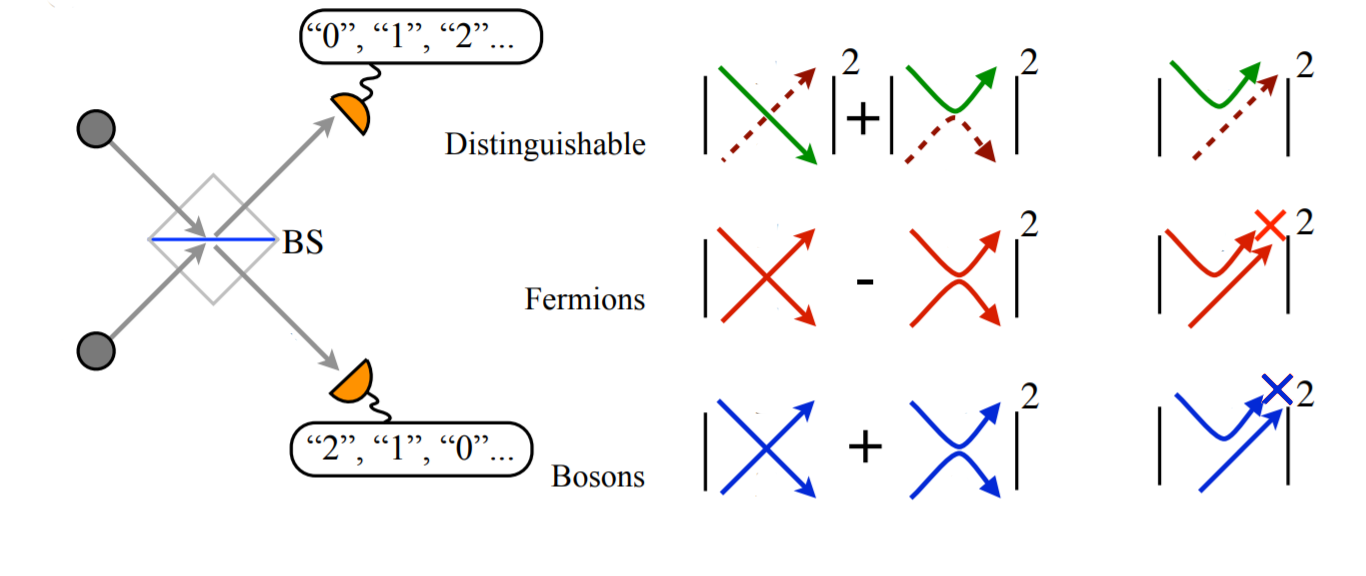
Bosons

Fermions

Qubits

Particle Interference

\mathrm{perm}\,U = U_{11} U_{22} + U_{12} U_{21}
\det U = U_{11} U_{22} - U_{12} U_{21}
U = \begin{pmatrix} U_{11} & U_{12} \\ U_{21} & U_{22} \end{pmatrix}

Hard!

Easy

Modified from Tichy, J. Phys. B 2014

\(n\) particles in \(m\) modes

U_{11}
U_{11}
U_{22}
U_{22}
U_{12}
U_{12}
U_{21}
U_{21}

if \(n \lesssim \sqrt{m} \)

no coincidence

coincidence

Pauli exclusion

Quantum Advantage by Boson Sampling

Based on certain plausible conjectures, Boson sampling is classically intractable (Aaronson & Arkhipov, STOC'11)

 

Wang et al., PRL 2019 performed Boson Sampling with 20 photons (6 lost) in 60 modes

 

photo credit

State-of-the-art classical simulation algorithms?

  • Boson sampling with 30 bosons in 900 modes can be classically simulated under 5 hours (Neville et al., Nat. Phys. 2017)
  • Clifford & Clifford SODA'18 gives an exact algorithm in \(O(n2^n + \mathrm{poly}(m,n))\) time

Classical Simulations of Boson Sampling

  • \(\log n\) remaining photons (followed from Clifford & Clifford's algorithm)
  • Constant loss + constant dark-count (Rahimi-Keshari, Ralph & Caves, PRX 2016)
  • Less than \(\sqrt{n}\) photons remaining (Oszmaniec & Brod, New J. Phys. 2018) and more scenarios (Brod & Oszmaniec, Quantum 2020)

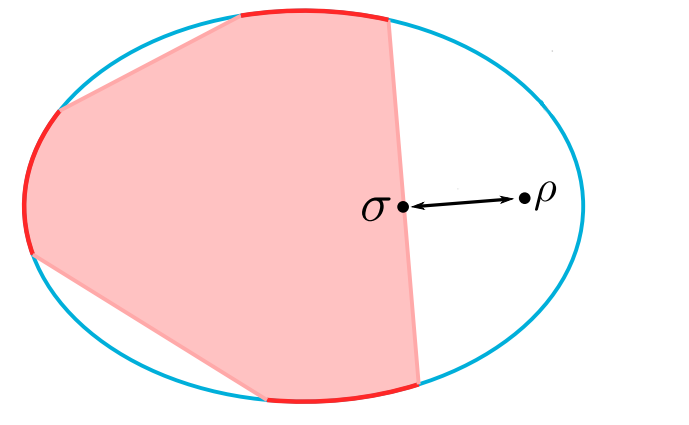
Q: How close are lossy states to classical simulable states on average?

Modified from Oszmaniec & Brod, New J. Phys. 2018

Classical

Quantum Advantage by Fermionic Linear Optics with Magic Inputs

(Passive) FLO operations such as fermionic SWAP are natural in superconducting architecture and quantum chemistry

  • Google's quantum supremacy circuits
  • Simulating electronic structure Hamiltonian (Kivlichan et al., PRL 2018)

photo credit

|0000\rangle + |1111\rangle

"Magic" input states promote FLO to universality (Bravyi, PRA 2006)

Q: Propose a feasible quantum advantage scheme with FLO; establish average-case hardness and anti-concentration

Zoltán Zimborás, Wigner RCP

Mauro Morales, UTS

Remark: although the two problems seem to be different, they both involve statements about averaging over the unitary group!

Movassagh, Cayley path and quantum computational supremacy

  • Boson sampling is classical intractable, while fermion sampling is classically simulable
  • Non-ideal boson sampling may be classically simulable (\(\leftarrow\) our project: extend the classical simulations)
  • Fermion sampling with magic inputs is classically intractable (\(\leftarrow\) our project: propose a quantum advantage scheme)

Summary