Topological Aspects of Chern-Simons TQFTs
Ninnat Dangniam
PHYS 523 Quantum Field Theory
16 December 2016
Anyons!
Motivation
- Abelian - Quantum memory
- Non-abelian - Quantum computation
Motivation
- Abelian - Quantum memory
- Non-abelian - Quantum computation
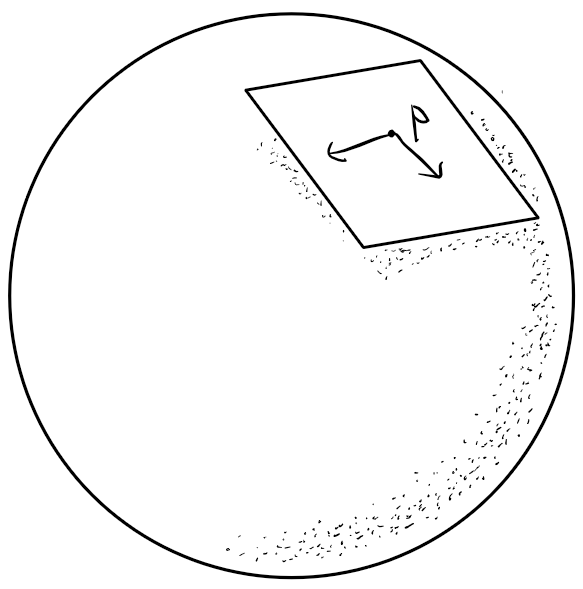
Manifold and Tangent Bundle
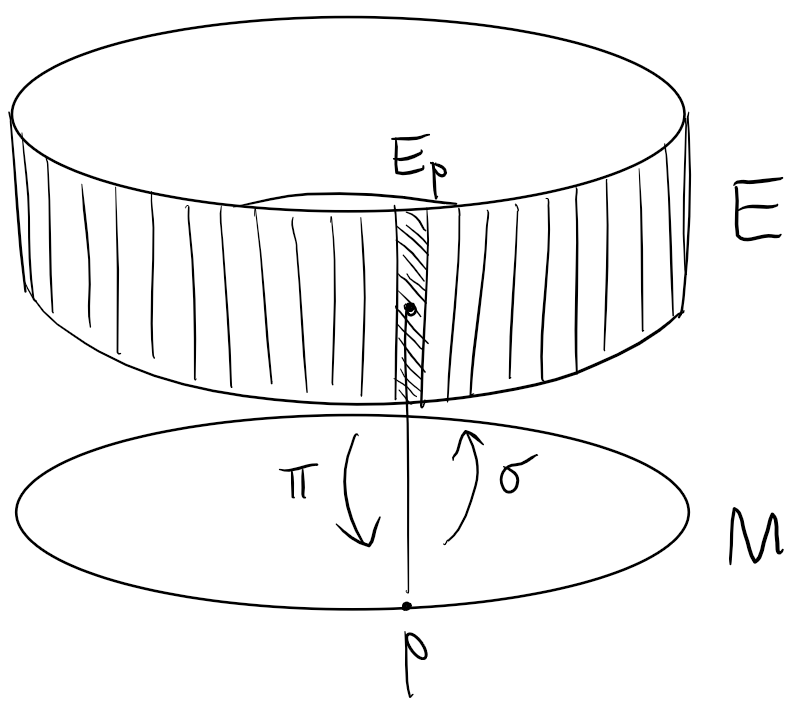
Fiber Bundle
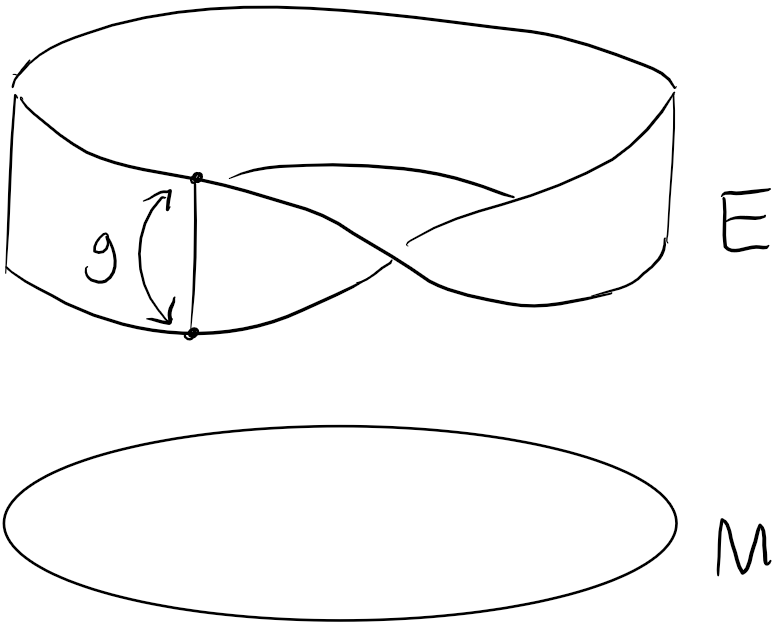
G-Bundle
Gauge Field
\nabla_{\nu} s = \nabla_{\nu} (s^{\mu} e_{\mu})
∇νs=∇ν(sμeμ)
= (\partial_{\nu} s^{\mu} +
=(∂νsμ+
Connection 1-Form
A^{\mu}{}_{\nu \rho}
Aμνρ
s^{\rho})e_{\mu}
sρ)eμ
\tilde{A}_{\mu} = g A_{\mu} g^{-1} + g \partial_{\mu} g^{-1}
A~μ=gAμg−1+g∂μg−1
g = e^{-if}
g=e−if
U(1) example
\tilde{A}_{\mu} = A_{\mu} + i \partial_{\mu} f
A~μ=Aμ+i∂μf
Gauge Transformation
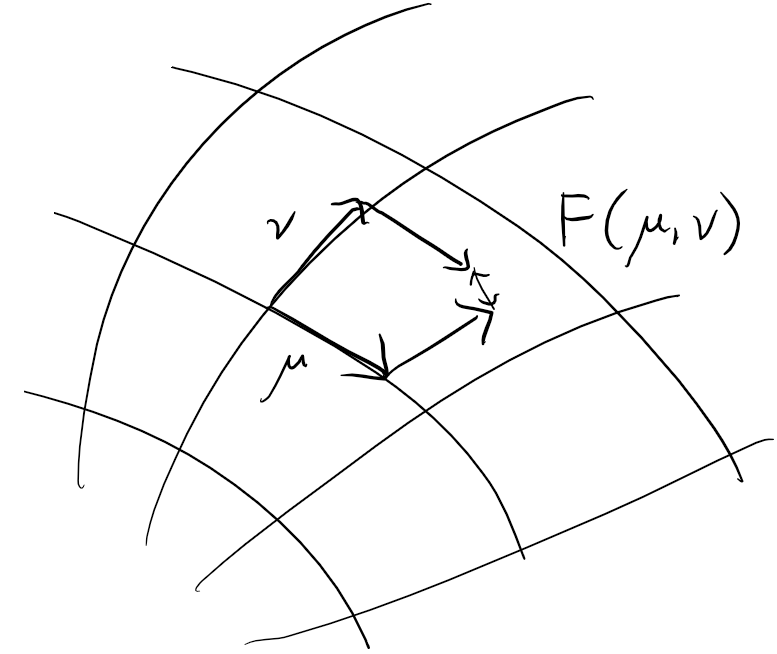
Curvature 2-form
F(\mu ,\nu) \equiv \nabla_{\mu} \nabla_{\nu} - \nabla_{\nu} \nabla_{\mu} - \nabla_{[\mu ,\nu]}
F(μ,ν)≡∇μ∇ν−∇ν∇μ−∇[μ,ν]
F_{\mu \nu} = \partial_{\mu} A_{\nu} - \partial_{\nu} A_{\mu} + [A_{\mu},A_{\nu}]
Fμν=∂μAν−∂νAμ+[Aμ,Aν]
F = dA + A \wedge A
F=dA+A∧A
Curvature 2-form
- The exterior derivative d generalizes Div, Grad, Curl
- The wedge product generalizes the cross product
F = dA + A \wedge A
F=dA+A∧A
Curvature 2-form
u_1 \wedge u_2 \wedge \cdots \wedge u_n = \mathcal{A} [u_1 \otimes u_2 \otimes \cdots \otimes u_n]
u1∧u2∧⋯∧un=A[u1⊗u2⊗⋯⊗un]
= \frac{1}{n!} \sum_{\sigma \in S_n} (-1)^{{\text sgn} \sigma} u_{\sigma(1)} \otimes u_{\sigma(2)} \otimes \cdots \otimes u_{\sigma(n)}
=n!1∑σ∈Sn(−1)sgnσuσ(1)⊗uσ(2)⊗⋯⊗uσ(n)
Think of wedge product explicitly as tensors
\mathcal{A} \left[ T_{j_1,j_1,...,j_n} \right] = \frac{1}{n!} \epsilon^{j_1,j_1,...,j_n} T_{j_1,j_1,...,j_n}
A[Tj1,j1,...,jn]=n!1ϵj1,j1,...,jnTj1,j1,...,jn
\mathcal{L}_{\text EM} = -\frac{1}{4} F_{\mu \nu} F^{\mu \nu}
LEM=−41FμνFμν
{\text Tr} (F \wedge F) ?
Tr(F∧F)?
Theory Without a Metric
Boring theory: 𝛿S vanishes for every A
{\text Tr} (F \wedge F) = d
Tr(F∧F)=d
Chern-Simons form
{\text Tr} (A \wedge dA + \frac{2}{3} A \wedge A \wedge A)
Tr(A∧dA+32A∧A∧A)
Chern-Simons Theory
S_{\text CS} = \frac{k}{4\pi} \int_M {\text Tr} (dA \wedge A + A \wedge A \wedge A)
SCS=4πk∫MTr(dA∧A+A∧A∧A)
S_{\text CS} \mapsto S_{\text CS} + 2\pi
SCS↦SCS+2π
k
k
n
n
Level
Almost gauge invariant!
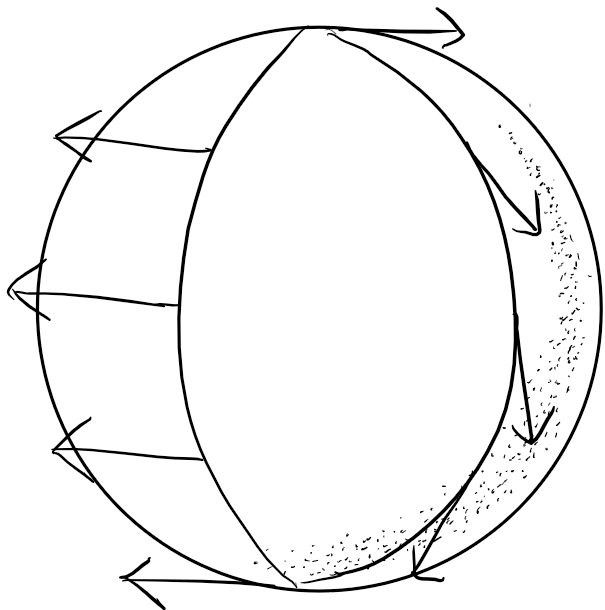
Holonomy
\nabla_{\gamma'(t)} u = 0
∇γ′(t)u=0
Holonomy
u(t) =
u(t)=
H(\gamma, A)
H(γ,A)
P\exp \left[-\int_0^t d\tau A(\tau) \right]
Pexp[−∫0tdτA(τ)]
u(0)
u(0)
H(\gamma, A') = g(\gamma(t)) H(\gamma, A) g^{-1}(\gamma(0))
H(γ,A′)=g(γ(t))H(γ,A)g−1(γ(0))
W(\gamma_{\text loop},A) = {\text Tr} (H(\gamma_{\text loop}, A))
W(γloop,A)=Tr(H(γloop,A))
Gauge invariant!
W(\gamma,A) = e^{iq\oint_{\gamma'} d\gamma \cdot A}
W(γ,A)=eiq∮γ′dγ⋅A
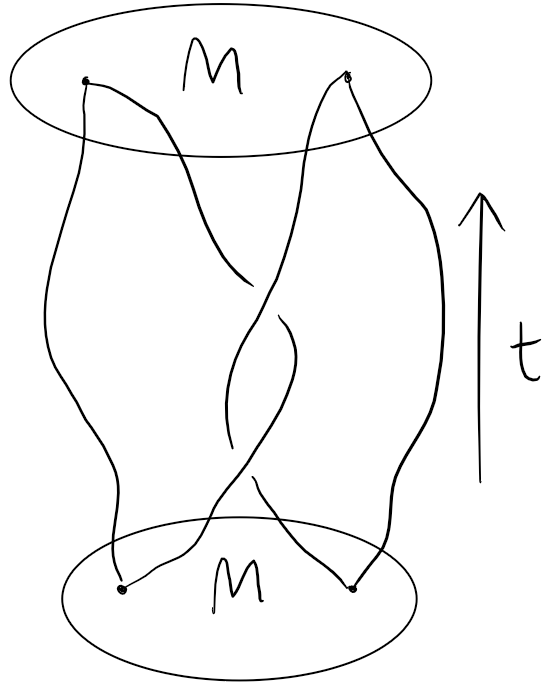
Abelian Chern-Simons Theory
\langle W(\gamma) \rangle = \frac{ \langle 0| W(\gamma) |0 \rangle }{ \langle 0|0 \rangle }
⟨W(γ)⟩=⟨0∣0⟩⟨0∣W(γ)∣0⟩
\langle W (\gamma) \rangle = \exp \left[ \frac{i \pi}{k} \sum_{j,l} q_j q_l L(\gamma_j,\gamma_k) \right]
⟨W(γ)⟩=exp[kiπ∑j,lqjqlL(γj,γk)]
= \frac{\int DA W(\gamma,A) \exp \left( i\int_M A \wedge dA \right)}{\int DA \exp \left( i\int_M A \wedge dA \right)}
=∫DAexp(i∫MA∧dA)∫DAW(γ,A)exp(i∫MA∧dA)
Abelian Chern-Simons Theory
\langle W (\gamma) \rangle = \exp \left[ \frac{i \pi}{k} \sum_{j,l} q_j q_l L(\gamma_j,\gamma_k) \right]
⟨W(γ)⟩=exp[kiπ∑j,lqjqlL(γj,γk)]
\langle W(\gamma) \rangle = \exp \left(\frac{2 i\pi q^2}{k} \right) \langle W(0) \rangle
⟨W(γ)⟩=exp(k2iπq2)⟨W(0)⟩
Trivial loop
Anyons!
Abelian Chern-Simons Theory
\langle W (\gamma) \rangle = \exp \left[ \frac{i \pi}{k} \sum_{j,l} q_j q_l L(\gamma_j,\gamma_l) \right]
⟨W(γ)⟩=exp[kiπ∑j,lqjqlL(γj,γl)]
\langle W(\gamma') \rangle = \exp \left( \frac{i\pi q^2}{k} L(\gamma,\gamma') \right) = e^{\frac{i\pi q^2}{k}} \langle W(0) \rangle
⟨W(γ′)⟩=exp(kiπq2L(γ,γ′))=ekiπq2⟨W(0)⟩
Trivial loop
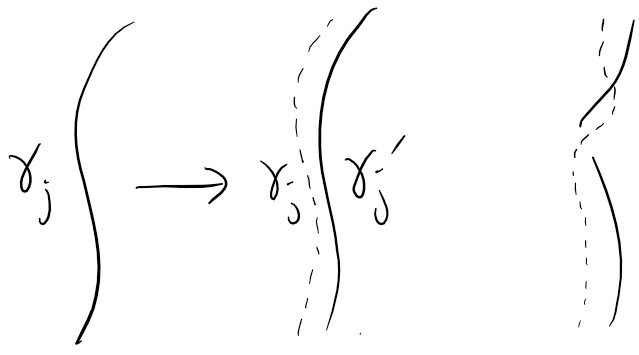
Framing
Abelian Chern-Simons Theory
\theta = \frac{\pi q^2}{k}
θ=kπq2
s = \frac{\theta}{2\pi}
s=2πθ
{\text spin} = \frac{q^2}{2k}
spin=2kq2
\langle W(\gamma') \rangle = \exp \left( \frac{i\pi q^2}{k} L(\gamma,\gamma') \right) = e^{\frac{i\pi q^2}{k}} \langle W(0) \rangle
⟨W(γ′)⟩=exp(kiπq2L(γ,γ′))=ekiπq2⟨W(0)⟩
Trivial loop
Framing
Topological Degeneracy
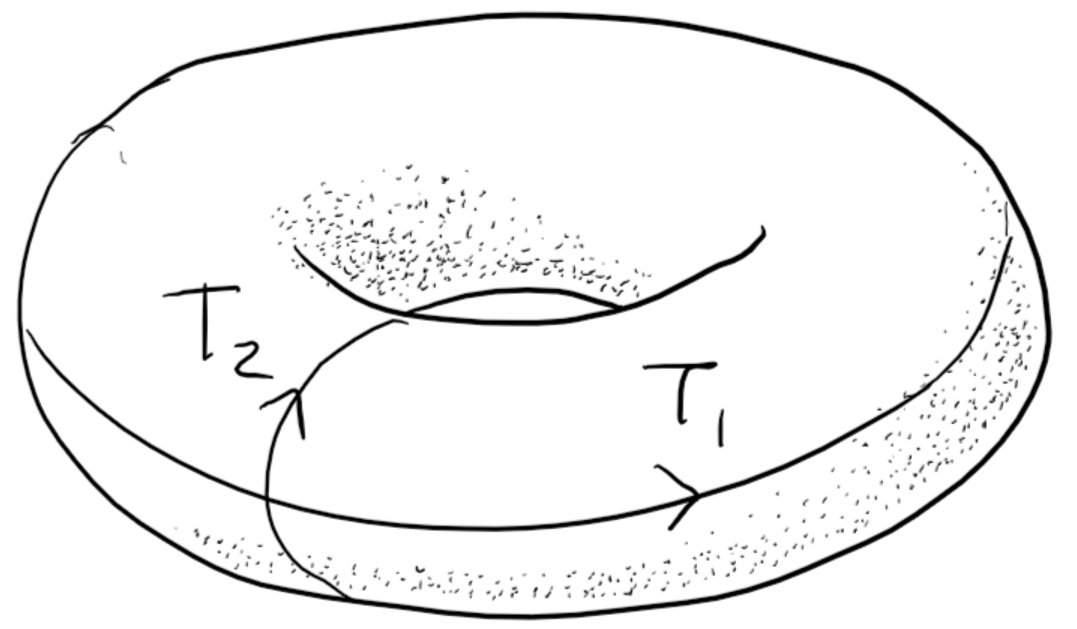
T_1, T_2
T1,T2
don't excite the ground state
Topological Degeneracy
T_2^{-1} T_1^{-1} T_2 T_1 = e^{2i\theta}I =
T2−1T1−1T2T1=e2iθI=
Topological Degeneracy
T_2 T_1 = e^{2i\theta} T_1 T_2
T2T1=e2iθT1T2
T_1 (T_2 |x\rangle) = e^{-2i\theta} T_2 T_1 |x\rangle
T1(T2∣x⟩)=e−2iθT2T1∣x⟩
= e^{-i (x + 2\theta)} (T_2 |x\rangle )
=e−i(x+2θ)(T2∣x⟩)
T_2 |x\rangle = |x+2\theta \rangle
T2∣x⟩=∣x+2θ⟩
\frac{2\pi p}{r} = 0,1,2,...,r-1
r2πp=0,1,2,...,r−1
Quantum Memory
-
John Baez and Javier P. Muniain, Gauge Fields, Knots, and Gravity
-
Jiannis K. Pachos, Introduction to Topological Quantum Computation
-
John Preskill, "Lecture Notes for Physics 229: Quantum Information and Computation"
Topological Aspects of Chern-Simons TQFTs Ninnat Dangniam PHYS 523 Quantum Field Theory 16 December 2016 Anyons!